[Перевод] Что внутри черного ящика: понимаем работу ML-модели с помощью SHAP
Значения Шепли применяются в экономике, а точнее — в теории кооперативных игр. Такие значения назначаются игрокам сообразно их вкладу в игру. В сфере машинного обучения идея использования значений Шепли нашла отражение во фреймворке SHAP (SHapley Additive exPlanations). Он представляет собой эффективный инструмент для интерпретации механизмов функционирования моделей.

Если вам интересны подробности о значениях Шепли — очень рекомендую обратиться к моей предыдущей статье, посвящённой математическим и интуитивным представлениям, раскрывающим смысл этих значений. И хотя в машинном обучении эти значения применяются по‑особенному, понимание базовых принципов, на которых они основаны, может оказаться полезным.
Использование значений Шепли во фреймворке SHAP напоминает их классическое применение тем, что они отражают индивидуальное влияние признаков на «игру» (другими словами — на модель машинного обучения). Но модели машинного обучения — это «игры», где нет «кооперирования» игроков, то есть — признаки не обязательно взаимодействуют друг с другом, как это происходило бы, будь они игроками в кооперативной игре. Вместо этого каждый из признаков вносит независимый вклад в результаты работы модели. Хотя тут может быть использована формула для нахождения значений Шепли, соответствующие вычисления могут оказаться слишком «тяжёлыми» и неточными. Это так из‑за большого количества «игроков» и из‑за того, что они могут объединяться в «союзы». Для того чтобы решить эту проблему, исследователи разработали альтернативные подходы. Среди них — метод Монте‑Карло и ядерные методы. В этом материале мы будем заниматься методом Монте‑Карло.
Начнём с примера. Предположим, имеется набор данных по стоимости 20 640 домов в Калифорнии.
from sklearn.datasets import fetch_california_housing
import pandas as pd
# загрузка набора данных
housing = fetch_california_housing()
X, y = housing.data, housing.target
X = pd.DataFrame(X, columns=housing.feature_names)
# подготовка признаков
X = X.drop(['Population', 'AveBedrms', 'AveOccup'], axis=1)Мы будем пользоваться следующими признаками: MedInc, HouseAge, AveRooms, Latitude и Longitude (Х).

Прогнозировать будем стоимость дома (y). Обратите внимание на то, что единицей измерения цен домов является $100 000.
Построим модель. Это может быть любая модель, но мы используем XGBoost (в этой моей статье вы можете найти сведения о математической базе XGBoost). Мы, следуя стандартной процедуре создания моделей, разделим данные на обучающий и тестовый наборы. Обучим модель с помощью обучающего набора данных.
# разделение данных на обучающий и тестовый наборы
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# обучение модели XGBoost
from xgboost import XGBRegressor
model = xgb.XGBRegressor(objective='reg:squarederror', random_state=4)
model.fit(X_train, y_train)Воспользуемся моделью для прогнозирования цен домов на тестовом наборе.
y_pred = model.predict(X_test)Продолжим разбираться с примером. Нам нужно узнать о том, какую стоимость модель спрогнозировала для первого образца (или для дома) в тестовом наборе. Выясним это:
X_test.iloc[0,]
MedInc 4.151800
HouseAge 22.000000
AveRooms 5.663073
Latitude 32.580000
Longitude -117.050000Вот какой ответ дала модель:
y_pred[0]
> 1.596
Прогноз, данный моделью, выглядит как некое таинственное значение, так как саму модель можно сравнить с чёрным ящиком. Того, что происходит внутри этого ящика, мы не видим. Для того чтобы получить больше информации о том, как именно было спрогнозировано итоговое значение, нам, для начала, надо понять две вещи:
Как признаки воздействуют на спрогнозированную цену дома — положительно или отрицательно? (Например — приводит ли наличие большего значения
MedIncк повышению спрогнозированной цены дома?)В какой степени значения признаков воздействуют на спрогнозированное значение? (Например — оказывает ли значение
MedIncбольшее воздействие на спрогнозированную цену дома, чем значениеAveRooms?)
Для того чтобы ответить на эти вопросы и определить вклад каждого из признаков в прогноз (в нашем случае — в число 1,596), можно обратиться к SHAP-значениям признаков.
Займёмся пошаговым вычислением SHAP-значения признака MedInc.
Шаг 0: Вычисление ожидаемой прогнозируемой цены дома
Ожидаемая прогнозируемая цена дома — это всего лишь среднее значение всех спрогнозированных значений:
y_pred.mean()
> 2.07В результате значение 2,07 играет роль ожидаемой прогнозируемой цены дома. Теперь попытаемся узнать о том, почему спрогнозированное значение 1,596 отклоняется от значения 2,07. Что является причиной расхождения в 0,476 (2,07–1,596)?
SHAP-значение признака позволяет измерить вклад признака в то, насколько предсказание модели отклоняется от ожидаемого прогнозируемого значения или приближается к нему.
Шаг 1: Выполнение случайных перестановок признаков
Начинаем со следующей последовательности признаков:

После их случайной перестановки получаем следующее:

Нас интересует признак MedInc — поэтому выделим этот признак и признак, находящийся справа от него:

Шаг 2: Выбор случайного образца из набора данных
Возвращаемся к тестовому набору данных и выбираем из него случайный образец данных:

Шаг 3: Формирование двух новых образцов
Эти образцы, частично, формируются из исходного образца…

А вот — новый образец, полученный на Шаге 2:

Первый созданный нами образец называется x1. Он будет содержать те же значения признаков, что и в исходном образце, за исключением значений, находящихся правее MedInc. Эти значения мы возьмём из нового образца данных.

Первые четыре значения здесь взяты из исходного образца, а последнее — из нового.
Второй образец, который мы создадим, называется x2. Он будет содержать те же значения признаков, что и исходный образец, за исключением тех, что находятся правее MedInc, а так же — за исключением самого MedInc.
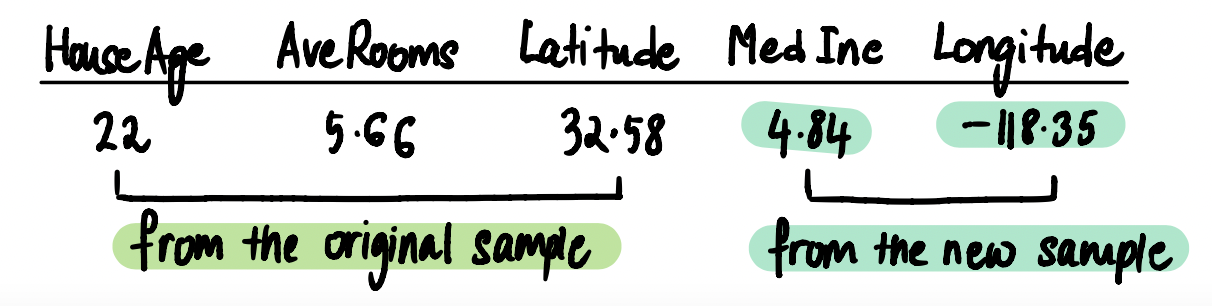
Первые три значения взяты из исходного образца, а MedInc и Longitude — из нового.
Из этого видно, что у нас получились два идентичных образца, которые различаются лишь в одной, очень важной для нас детали. Это — значение признака MedInc — того самого, который нас интересует.
Шаг 4: Использование новых образцов для формирования прогнозов и для нахождения различия в прогнозах
Теперь пропускаем полученные образцы через модель и получаем прогнозы по ним.
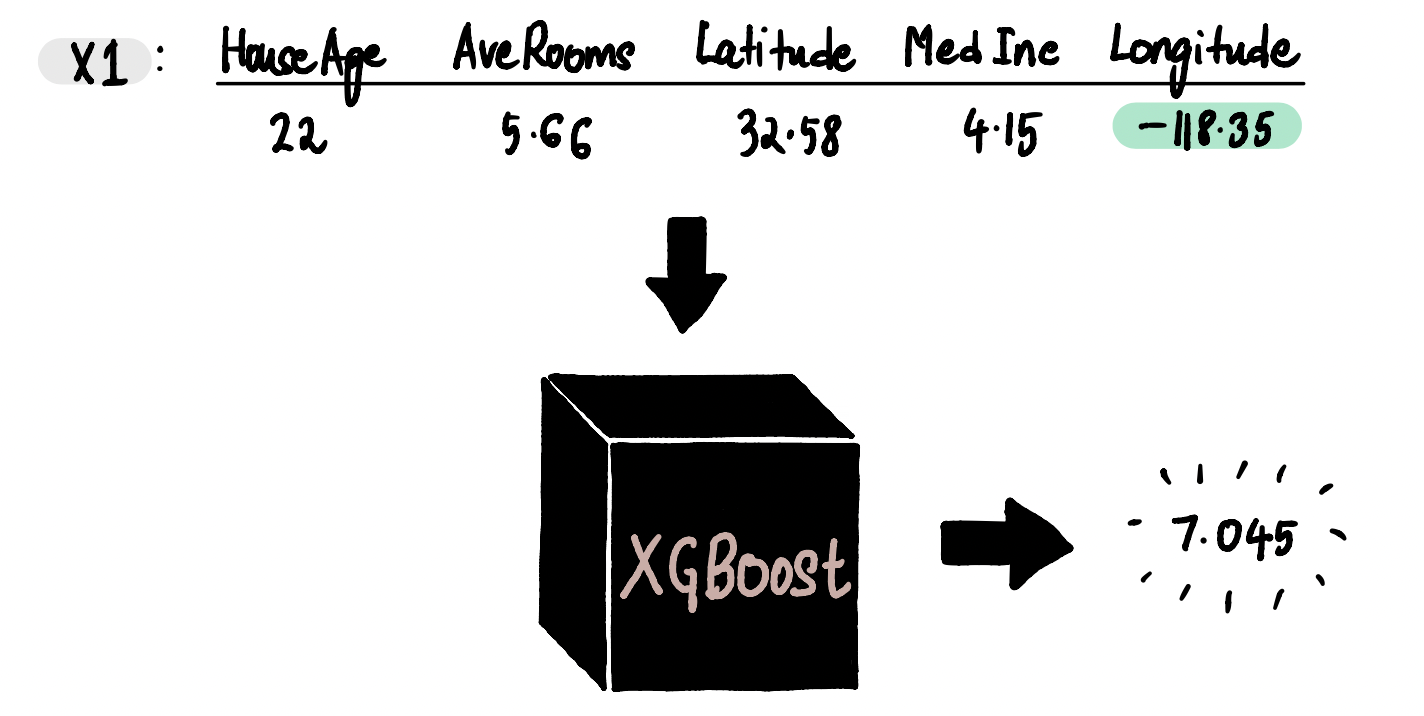

Находим разность полученных значений:
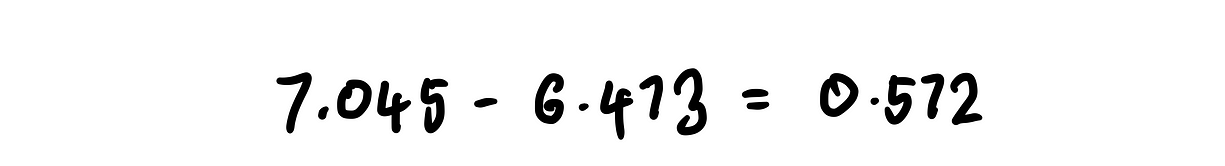
Так как образцы x1 и x2 отличаются лишь значением MedInc, полученная разность представляет собой изменение прогноза, произошедшее в результате изменения MedInc.
Шаг 5: Многократное повторение шагов 1–4 и вычисление среднего значения для полученных разностей
Теперь надо повторить вышеописанный процесс несколько раз и вычислить средний показатель разностей, полученных на Шаге 4.
Представим, что мы повторили этот процесс 1000 раз (это число может варьироваться в зависимости от сложности модели и набора данных). После усреднения результатов получено значение 0,22.
Это и есть SHAP-значение MedInc в первом образце. Оно указывает на то, что вклад MedInc в приближение ожидаемого прогнозируемого значения 2,07 к нашему прогнозу 1,596 составляет +0,22.
Тот же процесс нахождения SHAP-значений применим и к другим признакам — HouseAge, AveRooms, Latitude и Longitude.
Теперь, когда нам понятен принцип вычисления SHAP-значений, мы можем сопоставить их с нашими прогнозами путём визуализации данных. Сделать это можно с помощью объекта explainer из Python-библиотеки shap, передав ему входные данные модели.
import shap
explainer = shap.Explainer(model)
shap_values = explainer(X_test)В результате у нас будут SHAP-значения для всех признаков (MedInc, HouseAge, AveRooms, Latitude и Longitude) для каждого образца в тестовом наборе данных. Имея эти значения — приступим к их визуализации.
1. Диаграмма shap.plots.waterfall
Эта диаграмма позволит нам визуализировать индивидуальные SHAP-значения каждого образца в наборе данных. Построим диаграмму для первого образца.
# визуализация SHAP-значений для первого образца
shap.plots.waterfall(shap_values[0])
Обратите внимание на то, что ожидаемое прогнозируемое значение, E[f(X)] = 2,07, это значение, найденное на Шаге 0. А спрогнозированная цена первого дома, f(X) = 1,596, это значение, спрогнозированное для первого образца.
Отметим то, что SHAP-значение MedInc — это 0,22 (мы нашли его на Шаге 5), SHAP-значение признака Longitude — это -2,35, и так далее. Если сложить все эти значения, положительные и отрицательные, с 2,07, то получится спрогнозированное значение цены первого дома — 1,596.

Если не обращать внимание на знаки чисел, то окажется, что SHAP-значение для признака Longitude, 2,35, больше значений других признаков. Это указывает на то, что признак Longitude оказывает наиболее значительное влияние на этот прогноз.
Так же, как мы визуализировали SHAP-значения для первого образца, мы можем визуализировать его и для второго образца.
# визуализация SHAP-значений для второго образца
shap.plots.waterfall(shap_values[1])
Сравнивая SHAP-значения для признаков, описывающих в тестовом наборе данных первый и второй дома, мы видим то, что они сильно отличаются друг от друга. В случае с первым домом наибольшее влияние на его спрогнозированную цену оказал признак Longitude. А на спрогнозированную стоимость второго дома сильнее всего повлиял признак MedInc.
Обратите внимание на то, что различия SHAP-значений указывают на то, что в каждом случае каждый из признаков по-особенному влияет на выходные данные модели. Это очень важно понимать для укрепления доверия к процессу принятия решений, реализуемого моделью. Это позволяет обеспечить непредвзятость и беспристрастность результатов.
2. Диаграмма shap.plots.force
Ещё один способ визуализации интересующих нас значений — это диаграмма типа shap.plots.force.
shap.plots.force(shap_values[0])
3. Диаграмма shap.plots.bar, отражающая результаты усреднения SHAP-значений
Для того чтобы определить то, какие признаки, в целом, являются наиболее важными для прогнозов, выдаваемых моделью, можно использовать столбчатую диаграмму (shap.plots.bar), отражающую результаты усреднения SHAP‑значений по всем наблюдениям. Расчёт среднего на основании абсолютных значений показателей позволяет добиться того, чтобы положительные и отрицательные значения не уничтожали бы друг друга.
shap.plots.bar(shap_values)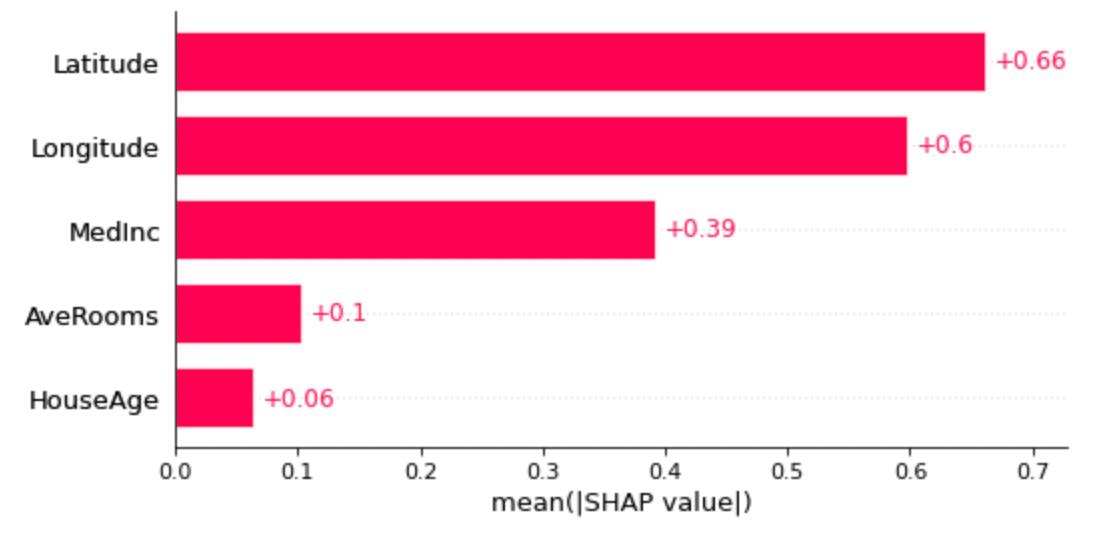
Каждому признаку соответствует свой элемент диаграммы, размер которого отражает среднее SHAP‑значение. Например, у нас получилось, что самое большое среднее SHAP‑значение имеет признак Latitude. Это указывает на то, что данный признак оказывает наиболее сильное воздействие на прогнозы модели. Эта информация поможет нам понять то, какие признаки являются наиболее важными в процессе принятия решений, реализуемом моделью.
4. Диаграмма shap.plots.beeswarm
Диаграмма shap.plots.beeswarm — это полезный инструмент, позволяющий визуализировать все SHAP‑значения для каждого признака. По оси x этой диаграммы SHAP‑значения сгруппированы по признакам. А цвет точек указывает на соответствующее значение признака. Обычно точки, цвет которых ближе к красному, указывают на более высокие значения признаков.
Диаграмма shap.plots.beeswarm может помочь в выявлении важных взаимоотношений между признаками и прогнозами модели. На нашей диаграмме признаки упорядочены по их средним SHAP‑значениям.
shap.plots.beeswarm(shap_values)
Исследуя SHAP‑значения на этой диаграмме, мы можем начать понимать природу взаимоотношений между признаками и спрогнозированными ценами домов. Например, в случае с признаком MedInc, видно, что SHAP‑значения растут по мере роста значения признака. Это указывает на то, что более высокие значения MedInc соответствуют более высоким спрогнозированным ценам домов.
Видна тут и обратная ситуация, связанная с признаками Latitude и Longitude. Здесь — чем больше значения признаков — тем меньше SHAP‑значения. Это наблюдение указывает на то, что более высокие значения Latitude и Longitude связаны с более низкими спрогнозированными ценами домов.
5. Диаграмма shap.plots.scatter и исследование взаимоотношений значений
Для того чтобы лучше понять взаимоотношения между отдельными значениями признаков и их SHAP‑значениями, можно создать диаграмму зависимости (shap.plots.scatter). Это — диаграмма, которая раскрывает взаимоотношения между SHAP‑значениями и значениями признаков для отдельных признаков.
shap.plots.scatter(shap_values[:,"MedInc"])
shap.plots.scatter(shap_values[:,"Latitude"])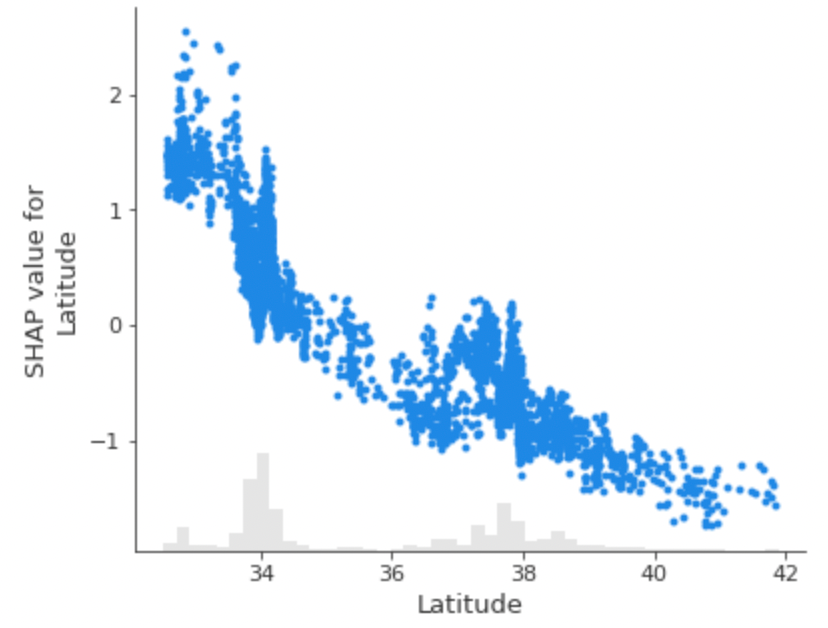
Анализируя диаграммы зависимости можно подтвердить наблюдения, сделанные при анализе диаграммы shap.plots.beeswarm. Например, когда мы создаём диаграмму зависимости для признака MedInc, мы отмечаем положительные взаимоотношения между значениями MedInc и SHAP‑значениями. Другими словами — более высокие значения MedInc приводят к повышению прогнозируемых цен домов.
В целом же диаграммы зависимости дают возможность лучше разобраться в сложных взаимоотношениях между отдельными признаками и спрогнозированными ценами домов.
Итоги

В результате можно сказать, что SHAP-значения дают нам возможность заглядывать в «чёрные ящики» моделей машинного обучения. Это позволяет получить представление о том, как именно каждый из признаков воздействует на выходные данные моделей. А ещё лучше во всём этом можно разобраться, используя инструменты визуализации данных. Фреймворк SHAP можно использовать для того чтобы принимать более осознанные решения относительно выбора признаков и улучшения моделей. Это — инструмент, позволяющий добиваться лучших результатов от используемых нами моделей машинного обучения.
О, а приходите к нам работать?
