[Перевод] Четыре способа обмануть нейросеть глубокого обучения02.02.2018 21:17

Нейросети используются уже довольно широко. Чат-боты, распознавание изображений, преобразование речи в текст и автоматические переводы с одного языка на другой — вот лишь некоторые сферы применения глубокого обучения, которое активно вытесняет другие подходы. И причина в основном в более широких возможностях обобщения при обработке больших объёмов данных.

А что насчёт целенаправленных атак? Можно ли использовать особенности работы нейросетей и создать такие данные, которые будут классифицироваться ошибочно? В этой статье мы рассмотрим несколько способов дополнения данных, которые сводят с ума нейросети глубокого обучения. И что ещё интереснее, эти данные для человека выглядят неизменёнными.

Структура статьи

В статье использован ряд исследовательских работ, посвящённых состязательному обучению (adversarial training).

Вам пригодятся базовые знания о нейросетях вроде градиентного спуска (Gradient Descent).

Объяснение и примеры использования состязательного обучения

Вероятно, это одна из первых работ, где продемонстрировано, как исказить пиксели изображения, чтобы классификатор принял ошибочное решение. В основе метода лежит факт, что изображения обычно представлены в виде 8-битных значений (каждый пиксель может иметь только одно целочисленное значение в диапазоне от 0 до 255, то есть в сумме 2⁸ значений). Следовательно, если искажения не превышают минимального значения, которое может быть представлено в изображении, то классификатор должен полностью их игнорировать и считать искажённое изображение неизменённым. Но авторы показывают, что это не так.

Они определяют ошибочную классификацию входных данных уравнением

$w^{\top }\widetilde{x}=w^{\top }x + w^{\top }\eta$

Здесь

$\widetilde{x}$ — входные данные, предназначенные для введения нейросети в заблуждение.

$w^{\top }x$ — выходные данные классификатора по неизменённому изображению (которое классифицируется корректно).

$\eta$ — этот компонент уравнения интереснее. Это специальный вектор, добавленный к исходным входным данным таким образом, чтобы вся сеть приняла ошибочное решение о классификации. То есть уравнение читается так: «Сеть может ошибиться в классификации, если к оригинальным входным данным добавлены такие данные, что получившийся результат заставляет нейросеть отнести его к другому классу». Это совершенно очевидное определение. Куда интереснее, как находить значение $\eta$ .

$\eta$ определяется так:

$sign(\bigtriangledown _{x}J(\theta, x, y))$

$sign()$ — это знаковая функция (sign function). Она отвечает лишь за знак значения. Если значение положительное, функция равна 1, если отрицательное, то –1.

$\bigtriangledown _{x}$ — это градиенты (относящиеся к входным данным).
$J$ — функция стоимости (cost function), используемая для обучения нейросети.
$\theta$ — параметры модели.
$х$ — входные данные.
$y$ — целевые выходные данные, то есть «ошибочный» класс.

Поскольку вся сеть является дифференцируемой, значения градиента можно легко найти с помощью метода обратного распространения ошибки (backprop).

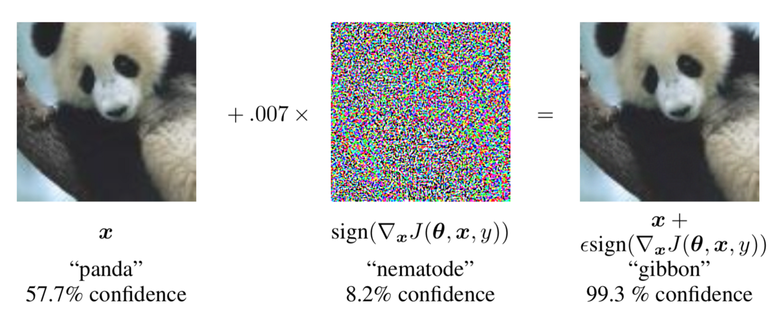
С помощью градиентных значений панда классифицируется ошибочно

Следовательно, изменив входные данные и выяснив с помощью анализа, какое направление нужно изменить (применив информацию о градиентах), можно легко заставить сеть неправильно классифицировать изображение. На картинке выше $\epsilon$ — величина градиентов, которые применяются к изображению (в данном случае $\epsilon$ равна 0,007).

Однопиксельная атака, призванная обмануть нейросети глубокого обучения

В предыдущей работе для обмана нейросети искались небольшие изменения для целого изображения. А здесь авторы пошли ещё дальше. Они утверждают, что не требуется изменять всё изображение. Вместо этого достаточно изменить небольшую часть, чтобы получившаяся картинка была ошибочно отнесена к другому классу.

Для заданных входных данных $x$ вероятность принадлежности $x$ к классу $t$ равна $f_x()$ . Задача описывается уравнением

$\begin{matrix}maximize\\e(x)* \end{matrix} f_{adv}(x+e(x))$

$adv$ — оптимизируемый вредоносный класс (adversarial class).
$e(x)$ — вредоносные данные (adversarial data) (такие же, как в предыдущей работе), которые добавляются ко входным данным. Однако в данном случае у $e()$ есть ограничение:

$||e(x)||_{0} \leq d$

Эта формула означает, что количество элементов в векторе $х$ должно быть меньше настраиваемого параметра $L$ . $||_{0}$ означает нулевую норму (0th norm) — количество ненулевых элементов в векторе. Максимальное значение элементов, генерируемых $e()$ , ограничено, как и в предыдущей работе.

Как найти правильный вектор нападения

В предыдущей работе для оптимизации ради получения правильных значений вредоносных данных использовался метод обратного распространения ошибки (backprop). Я считаю, что нечестно давать доступ к градиентам модели, поскольку становится возможным понять, как именно «думает» модель. Следовательно, облегчается оптимизация для вредоносных входных данных.

В данной работе авторы решили их не использовать. Вместо этого они прибегли к дифференциальной эволюции (Differential Evolution). При таком методе берутся образцы, на основе которых генерируются «дочерние» образцы, а из них потом оставляют лишь те, что получились лучше «родительских». Затем выполняется новая итерация генерирования «дочерних» образцов.

Это не позволяет получить информацию о градиентах, и находить правильные значения для вредоносных входных данных можно, не зная, как работает модель (это возможно, даже если модель не будет дифференцируемой, в отличие от предыдущего метода).
Вот что получилось у авторов:

Результат однопиксельной атаки. В картинках изменено всего по одному пикселю, и в результате нейросеть классифицировала их неправильно. В скобках указана ошибочная категория после атаки

Для CIFAR 10 значение $L$ оставалось равным $1$ , то есть изменять можно было только один пиксель. А конкурент смог обмануть классификатор, и тот относил изображения к совершенно другим классам.

Вредоносная заплатка

Вредоносная заплатка (adversarial patch) — совсем свежая (и очень популярная) методика генерирования вредоносных изображений. В предыдущих двух методиках вредоносные данные добавлялись к исходным входным данным. Это означает, что вредоносные данные зависят от самих входных данных.

Авторы вредоносной заплатки подбирают некие данные, которые подходят для всех изображений. Термин «заплатка» в данном случае нужно понимать буквально: это изображение меньшего размера (относительно входных изображений), которое накладывается поверх входных, чтобы обмануть классификатор.

Оптимизация работает в соответствии с этим уравнением:

$\widehat{p}=arg \max_{p} \mathbb{E}_{x \sim X,t \sim T,l \sim L}[log Pr(\widehat{y}|A(p,x,l,t))]$

$\widehat{p}$ — подобранная заплатка.
$\widehat{y}$ — целевой (т. е. ошибочный) класс.

Здесь интересно вот что:

$A(p,x,l,t)$

Это функция применения заплатки. По сути, она просто решает (случайным образом), куда и как накладывать заплату на входное изображение. $p$ — сам патч. $x$ — входное изображение. $l$ — место наложения заплаты. $t$ — преобразование заплаты (например, масштабирование и вращение).

Важно отметить, что применительно к вышеприведённому уравнению система обучалась на всех изображениях в датасете (ImageNet), на всех возможных преобразованиях. И заплата обманывала классификатор на ВСЕХ изображениях датасета. Это главное отличие данного метода от двух предыдущих. Там нейросеть обучалась на одном изображении, а этот метод позволяет подобрать заплату, которая работает на большой выборке картинок.

Заплатку можно легко оптимизировать с помощью метода обратного распространения ошибки.

Попробуйте сами

В авторской работе приведено изображение заплатки, которую можно накладывать на ваши изображения для обмана классификатора. Заплатка сработает, даже если распечатать и положить её рядом с физическим объектом.

«Вы это слышали»? Атака на системы распознавания речи

Обдурить можно не только модели, классифицирующие изображения. Авторы этой работы демонстрируют, как ввести в заблуждение модели автоматического распознавания речи.

Особенность звуковых данных в том, что входные данные нельзя легко изменить с помощью метода обратного распространения ошибки. Причина в том, что входные данные для звукового классификатора проходят через преобразование, для которого требуется вычислить коэффициенты косинусного преобразования Фурье (Mel Frequency Cepstral Coefficients, MFCC), они затем используются в качестве входных данных для модели. К сожалению, вычисление MFCC не является дифференциальной функцией, поэтому оптимизировать входные данные с помощью метода обратного распространения ошибки не получится.

Вместо этого авторы использовали генетический алгоритм, аналогичный рассмотренному выше. Входные родительские данные модифицируются, в результате получаем дочерние данные. Сохраняются те «потомки», которые лучше обманывают классификатор; они, в свою очередь, тоже модифицируются, и так раз за разом.

Заключение

Глубокое обучение — превосходный инструмент, и он будет использоваться всё шире. И очень важно знать, каким образом можно обмануть нейросети, заставив их неверно классифицировать. Это позволяет оценить границы предположительного обмана подобных систем и найти способы защиты.

Ещё один метод обмана разработан в MIT, но работа пока не опубликована. Утверждается, что этот метод позволяет добиться 1000-кратного ускорения генерирования вредоносных входных данных. Анонс исследования можно посмотреть здесь.