[Перевод] Четыре новых атаки на схему безопасного обмена ключами KLJN
В этой статье мы рассмотрим четыре новых статистических атаки на схему безопасного обмена ключами KLJN (Кирхгофа-Лоу-Джонсона). В атаках используются генераторы случайных чисел. Мы рассмотрим несколько вариантов знакомства «хакера» с информацией о двух устройствах приема-передачи.
1. Как строится защищенное соединение
Одним из способов обеспечения безопасности связи является шифрование, то есть преобразование открытого текста в зашифрованный с помощью шифра. Предположим, Алиса и Боб (рис. 1) хотят обмениваться между собой некоторой информацией через сеть с публичным доступом. Для обеспечения безопасности они используют ключ — секретную строку из рандомных битов, известную им обоим. Этот ключ используется как для шифрования, так и для дешифрования текста.

Зашифрованное сообщение является некой функцией от открытого текста Р и ключа К:
В криптографии с симметричным ключом для дешифрования используется обратная функция:
Перед началом работы протокола шифрования сторонам необходимо обменяться ключом, используя другой тип безопасного обмена. Безопасность передачи данных напрямую зависит от безопасности передачи защищенного ключа по каналу связи.
Пусть наш канал прослушивает Ева (рис. 1), которая имеет всю информацию о наших устройствах, их протоколах и алгоритмах. Ее цель — перехватить ключ безопасности. В идеальной ситуации ключ надежно генерируется и передается, а сразу после использования уничтожается.
Мы рассмотрим атаки на безопасный обмен ключами Кирхгофа-Лоу-Джонсона (KLJN) на основе генераторов случайных чисел (RNG), подразумевающих шумы сообщающихся сторон.
2. Схема KLJN
Система KLJN представляет собой физическую схему, основанную на тепловом шуме резисторов, используемая для обмена ключами. Она состоит из четырех резисторов, двух генераторов шума и четырех вольтметров. На рис. 2 показана схема KLJN. Две общающиеся стороны, Алиса и Боб, соединены проводом. У них одинаковые пары резисторов, RA и RB. Статистически независимые напряжения теплового шума UH, A (t), UL, A (t) и UH, B (t), UL, B (t), представляют напряжения шума резисторов RH и RL (RH > RL) Алисы и Боба соответственно.
Они часто генерируются с помощью генераторов случайных чисел. В начале каждого периода обмена битами Алиса и Боб случайным образом выбирают один из своих резисторов для подключения к проводу.

В протоколе, основанном на напряжении, они измеряют среднеквадратичное напряжение провода. Теоретически среднеквадратическое напряжение провода определяется формулой Джонсона,

где Tэф — общая эффективная температура, Rp — параллельное результирующее сопротивление Алисы и Боба, которое находится по формуле
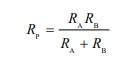
delta f — шумовая полоса генераторов, имитирующих тепловой шум.
При выборе резисторов Алисой и Бобом возможны четыре возможных битовых ситуации: HH, LL, LH и HL. Из формулы Джонсона это приводит к трем возможным уровням среднеквадратичного напряжения, как показано на рис. 3. Ситуации битов HH и LL небезопасны, потому что они отображаются с различным среднеквадратичным напряжением. Алиса и Боб отбрасывают эти периоды. С другой стороны, битовые ситуации LH и HL безопасны, потому что они выдают такое же среднеквадратичное напряжение. Ева не может различить битовые ситуации LH и HL, но Алиса и Боб может, потому что они знают, какой резистор они выбрали.

Битовые ситуации HH и LL небезопасны, потому что они отображают в среднеквадратичном напряжении, значение которого легко определяется. Алиса и Боб отбрасывают эти биты.
Популярность KLJN обусловлена тем, что такая схема может быть легко изготовлена. Недостатоком же KLJN является наличие нескольких способов атак, в которых нарушается безопасность. Было предложено несколько атак против схемы KLJN, но каждая известная атака была либо идейно или экспериментально неверной, либо для нее имелась подобранная схема защиты. В этой статье мы предлагаем четыре атаки, позволяющие перехватить передачу ключа при такой схеме.
Существует два вида практических генераторов случайных чисел: истинные (в зависимости от некой величины физической среды) и вычислительные. Вычислительные ГСЧ пытаются генерировать выходные данные так, чтобы они были практически неотличимы от случайных. Такие ГСЧ используют входные потоки, и при перехвате начальных данных выходная последовательность перестает быть неизвестной.
Существуют различные ГСЧ-атаки на условно защищенные каналы передач данных. Безопасное соединение также требует истинных случайных чисел для полной безопасности. В нашем случае мы используем в качестве физической величины среды напряжение шумов Алисы и Боба для генерации случайных чисел. На выходе мы получаем шум, который используется в аналоговой передаче данных.
Рассмотрим две ситуации взлома, когда Ева знает входные значения только одной из сторон либо обеих.
Двустороннее знание
Еве известны амплитуды генераторов шумового напряжения с обеих сторон. В этом случае используется перекрестная корреляционная атака.
Для четырех возможных комбинаций резисторов, HL, LH, LL и HH, Ева настраивает симулятор, используя свои шумы (которые коррелируют с соответствующими шумами Боба Алисы), и она записывает результирующие напряжения проводов UHH (t), ULL (t), UHL (t) и ULH (t). Затем она оценивает взаимную корреляцию между измеренным напряжением Uw (t) Алисы и Боба и моделируемыми. Для напряжения и тока на проводе верны следующие формулы:
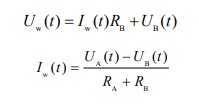
Коэффициент взаимной корреляции для случая, например, НН ищется по формуле:
Случай с наибольшей перекрестной корреляцией и является наилучшим для нас. Аналогичным образом рассчитывается взаимная корреляция для тока, после чего находится максимальное значение коэффициента. Для протокола мощности канала Ева имеет в своем распоряжении измеренные Uw (t) и Iw (t). Она использует свои шумы для имитации четырех возможных форм волны: PHH (t), PLL (t), PHL (t) и PLH (t). Для моделируемого случая мощность рассматривается как произведение напряжения и тока.
Возможен также вариант корреляционной атаки напрямую. Ева измеряет напряжение и ток, и по полученным значениям, используя закон Ома, рассчитывает возможные падения напряжения на сопротивлениях Алисы/Боба RH и RL по правилу Кирхгофа для узла. Таким образом, мы получаем гипотетические амплитуды напряжения шума Алисы/Боба. С помощью этих данных мы проверяем четыре гипотезы:
Гипотеза (i): Алиса выбрала RL
Гипотеза (ii): Алиса выбрала RH
Гипотеза (iii): Боб выбрал RL
Гипотеза (iv): Боб выбрал RH
Для проверки гипотез мы находим взаимную корреляцию для 1–2 и 3–4, и выбираем случай максимальной.
Одностороннее знание
Пусть Ева частично знает только о шумах Алисы, то есть о выходах генератора шума
резисторов Алисы, UL, A (t) и UH, A (t). Напряжение генератора Боба ей совершенно неизвестно.
Методы взаимной корреляционной атаки работают и здесь, с незначительными изменениями, как описано ниже.
Ева генерирует два независимых «фиктивных» тепловых шума для замены неизвестных напряжений шума Боба UH, B (t) и UL, B (t). Затем она использует протокол, соответствующий двустороннему случаю: она измеряет Uw (t) и Iw (t). Затем, исходя из Iw (t), она вычисляет гипотетическое падение напряжение на возможных вариантах сопротивлений RH и RL Алисы. С помощью этих данных она проверяет две гипотезы:
Гипотеза (i): Алиса выбрала RL
Гипотеза (ii): Алиса выбрала RH.
Обратим внимание, что в двустороннем случае она знала о шумах Боба, поэтому она могла сформулировать четыре гипотезы, в то время как в одностороннем случае она знает только напряжения генератора Алисы, поэтому она может сформировать только две гипотезы.
Аналогичным образом вычисляется максимальный коэффициент взаимной корреляции. Далее Ева оценивает измеренное среднеквадратичное напряжение на проводе в течение всего периода обмена битами. Исходя из этого значения, используя формулу Джонсона, она оценивает параллельное результирующее сопротивление Rр Алисы и Боба. Из Rр и RA она вычисляет RB по формуле

Таким образом, схема KLJN взломана. Мы получили четыре новых способа взломать схему передачи KLJN. Защита от таких атак заключается в использовании истинных генераторов случайных чисел (с достаточной устойчивостью к несанкционированному вмешательству), о которых мы уже говорили ранее.
