[Перевод] Алгоритмы сжатия данных без потерь: что они говорят о рынках

В нашем блоге на Хабре мы не только рассматриваем различные технологии финансового рынка, но и описываем различные инструменты, использующиеся аналитиками в ходе его анализа. В частности, не так давно мы писали о том, как гипотезу случайного блуждания можно использовать для прогнозирования состояния финансового рынка. Количественный аналитик хедж-фонда NMRQL Стюарт Рид опубликовал на сайте Turing Finance результаты своего исследования, где применил эту гипотезу для тестирования случайности поведения рынков.
Идея заключалась в следующем: генераторы случайных чисел «прогоняются» через группу тестов NIST, чтобы понять, где возникает уязвимость, позволяющая использовать неэффективность рынка для извлечения прибыли. В ходе эксперимента автор пришел к выводу, что поведение рынка нельзя описать в терминах простого подбрасывания монетки, как считают отдельные авторитетные ученые. Некоторым тестам удалось зафиксировать определенный уровень «шума» в поведении рынка. Один из них — тест на линейную сложность — привлек внимание автора, поскольку напоминает об идее отношения случайности и степени сжатия.
В новой статье Рид попытался выяснить, какую пользу могут принести алгоритмы сжатия данных для поставленной ранее задачи. Мы представляем вашему вниманию адаптированный перевод этой работы.
Эффективность рынка и гипотеза случайного блуждания
В своем крайнем выражении гипотеза эффективности рынка утверждает, что вся информация, будь то публичная или доступная частным лицам, мгновенно и точно учитывается в значении цены. Поэтому любой прогноз цен назавтра должен основываться на сегодняшнем состоянии рынка, так как текущие котировки верно и достаточно полно отражают текущее положение дел.
Согласно этой теории, никакой подробный экономический или фундаментальный анализ прошлого не даст более точный прогноз на будущее. На эффективном с точки зрения полноты и достаточности информации рынке будущее не определено, потому что зависит от неизвестных данных, которые появятся «завтра». Исходя из позиции сегодняшнего наблюдателя, будущие изменения случайны. «Взломать» рынок способны лишь аналитики, умеющие путешествовать во времени.
Эта гипотеза имеет свои достоинства, даже если мы будем выступать за более сложное понимание ситуации, за влияние эволюционных и поведенческих факторов. Заслуги этой теории неоспоримы. Во-первых, предсказывать поведение рынков действительно сложно. Во-вторых, действительно не существует последовательности действий, по которой среднестатистический игрок способен взломать рынок. В-третьих, гипотеза эффективности вполне логично объясняет появление таких финансовых инноваций, как, например, производные инструменты.
Самая серьезная критика гипотезы эффективности идет со стороны поведенческого финансового анализа, который подвергает сомнению ее фундаментальные постулаты. В рамках этого подхода утверждается, что инвесторы не ведут себя рационально и не способны давать «справедливую» цену акциям. У игроков на практике нет единых ожиданий по поводу цены.
Эволюционная теория развития рынков добавляет к этому еще пару аргументов. Она считает, что система состоит из разрозненных агентов, которые взаимодействуют между собой, подчиняясь эволюционным законам. В этом взаимодействии на первый план выходят случайность, моментум, стоимость и оборот активов (реверсия). Ни один из этих критериев оценки не преобладает над остальными. Их влияние на состояние рынка меняется по мере того, как игроки приспосабливаются к их воздействию. Гипотеза эффективности называет такие вещи аномалиями рынка, что не совсем соответствует действительности. Их появление вполне предсказуемо, а влияние на рынок может быть оценено количественно.
В ответ на критику приверженцы эффективности рынка разработали две новых гипотезы. Одна утверждает, что только публичная информация отражается в котировках. Другая доходит до того, что признает влияние исторических данных на текущие цены акций. Но главная позиция остается прежней: движение цен следует распределению цепи Маркова, случайному блужданию.
Получается, что мы дублируем гипотезу случайного блуждания, лежащую в основе почти всех современных моделей цен. Академики и практики рынка тратят десятилетия на изучение относительной эффективности и случайности рынков. В прошлой статье Стюарт Рид представил один из тестов для проверки случайности — тест неоднородного дисперсионного отношения Ло и МакКинли. В этот раз среди прочего речь пойдет об алгоритме сжатия Лемпеля-Зива.
Алгоритмическая теория информации и случайность
Для количественного анализа изучение случайности не в новинку. Этим давно занимаются криптография, квантовая механика, генетика. Неудивительно, что некоторые идеи и подходы были заимствованы из этих наук. Например, из алгоритмической теории информации экономисты взяли идею о том, что случайная последовательность несжимаема. Давайте попытаемся для начала установить контекст этой интересной мысли.
В 1930-х Алан Тьюринг представил абстрактную модель вычислений, которую назвал автоматической машиной. Сегодня она известна как машина Тьюринга. В этом отношении нам интересно лишь следующее утверждение: «Неважно, какие алгоритмы вычисления закладываются, машина должна имитировать саму логику алгоритма».

Модель машины Тьюринга
В своей упрощенной форме алгоритм есть детерминистическая последовательность шагов для трансформации набора входных данных в набор выходных. Для последовательности чисел Фибоначчи такой алгоритм построить легко: следующее число есть сумма двух предыдущих. Согласно другому великому математику Андрею Колмогорову, сложность последовательности может быть измерена через длину самой короткой вычислительной программы, которая генерирует эту последовательность как выходную. Если эта программа короче первоначальной последовательности, значит, мы сжали последовательность, то есть закодировали ее.
Что происходит, когда мы закладываем в машину Тьюринга случайную последовательность S? Если нет логики в распределении данных, машине нечего симулировать. Единственный вариант получить на выходе случайную последовательность — print S. Но эта программа длиннее, чем случайная последовательность S. Поэтому ее сложность, по определению, выше. Вот что имеют в виду, когда говорят, что случайная последовательность несжимаема. Другой вопрос, чем мы можем подкрепить факт, что найденная нами программа самая короткая из возможных? Для того чтобы прийти к такому выводу нам следовало бы перебрать бесконечное число комбинаций.
Проще говоря, сложность Колмогорова не вычислима. Следовательно, случайность не вычислима. Мы не можем доказать, что последовательность случайна. Но это не значит, что мы не способны протестировать возможность того, что последовательность может быть случайна. Здесь в игру вступают статистические тесты случайности, некоторые из которых используют алгоритмы сжатия.
Компрессия и случайность рынка: постановка проблемы
Всего лишь несколько ученых пытались приспособить алгоритмы сжатия для проверки эффективности рынков. Сама по себе идея проста, но за этой простотой скрываются специфические вызовы.Вызов 1: конечная последовательность и бесконечность
Наше определение случайности в информационной теории означает, что нам приходится иметь дело с бесконечной протяженностью. Любая конечная последовательность может быть слегка сжата уже на основе одной только вероятности. Когда мы используем компрессию для проверки относительно коротких последовательностей на рынке, нам нет дела, способен ли алгоритм сжать их. Нам интересно, будет ли уровень сжатия статистически значим.Вызов 2: дрейф рынка
Есть несколько типов случайности. Первый тип называется мартингейлом или действительной случайностью Колмогорова. Его чаще всего ассоциируют с компьютерными науками и информационной теорией. Второй тип — случайность Маркова, используемая в финансовом анализе и гипотезе случайного блуждания.
Это значит, что мы должны быть предельно осторожны, когда выбираем статистический тест для рыночной случайности. Статистический тест, разработанный под первый тип случайности, будет иметь интервал доверия, отличный от того, который есть у теста под случайность Маркова.
Сейчас должно немного проясниться. Допустим, у нас есть две модели: броуновское движение и геометрическое броуновское движение с ненулевым отклонением. В нашем примере первая модель подходит для обоих типов случайности. Вторая лишь для случайности Маркова. Результат теста второй модели будет искажен.
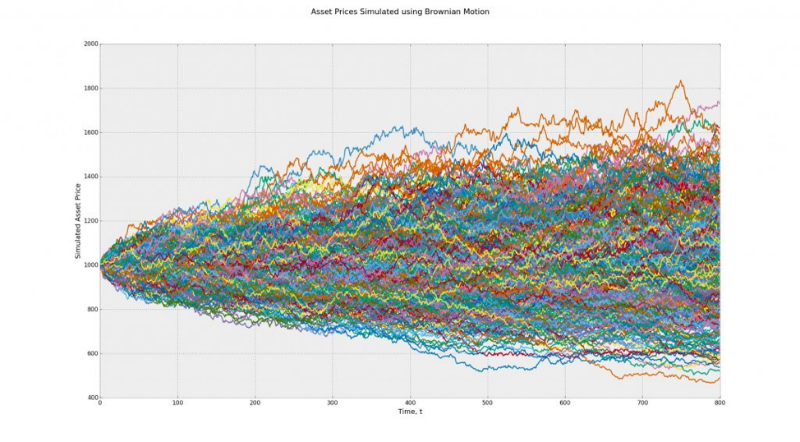
Модель 1 (Броуновское движение) — в среднем, все пути ведут в никуда, при нулевом отклонении. При бинаризации эта модель превращается в последовательность подбрасывания монеты
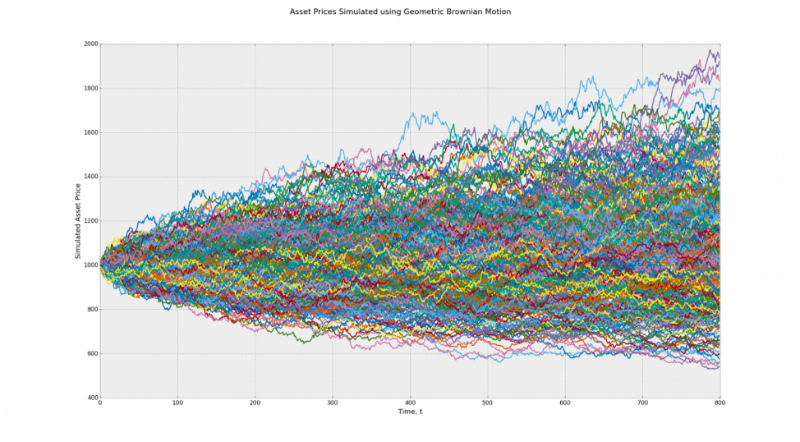
Модель 2 (Геометрическое Броуновское движение) — пути ведут вверх, а отклонение является ненулевым. При бинаризации в результаты будет вноситься искажение
Это серьезная проблема для тех, кто хочет опровергнуть гипотезу случайного блуждания через компрессию. Поскольку теория имеет дело лишь с избыточной предсказуемостью дрейфа рынка, то есть способности кого-то рынок взломать.
Вызов 3: стохастическая волатильность и разрывы
Следующая проблема заключается в том, что нестационарность волатильности может привести к тому, что определенные движения рынка будут выглядеть как регулярные и частые явления вопреки теоретическим выкладкам. Эту проблему еще называют «толстые хвосты». Если мы предположим, что шум рыночных изменений стремится к нулю, независимо от разрывов и стохастической волатильности, мы можем представить изменения в двоичном коде и снять проблему.
Тест сжатия для рыночной случайности
В академической науке алгоритмы сжатия данных без потерь в отношении оценки эффективности рынка уже применялись. Суть большинства исследований сводится к следующему: развитые рынки демонстрируют высокий уровень эффективности, развивающиеся рынки демонстрируют избыточную сжимаемость и определенный уровень неэффективности. Эти неэффектиновсти можно объяснить лишь через специфические паттерны, которые показывают уровень вероятности выше ожидаемого на определенных временных интервалах.Методология проверки
Методология основана на трех известных алгоритмах сжатия: {gzip, bzip2 и xz}.
- Нужно загрузить рыночные индексы с Quandl.com.
- Затем рассчитывать логарифмические возвраты индексов и обозначить их как r.
- Подсчитать их среднее (компонент отклонения) — μr.
- Для снятия направленности (детренд) r из него вычитывается μr.
- Затем r переводится в двоичную систему, замещая значения больше нуля единицей, а значения меньше нуля, соответственно, нулем.
- Затем r разделяется на m через наложение дискретных окон — W по 7 лет каждое.
- Каждое окно конвертируется в шестнадцатеричное wh (4-дневная субпоследовательность).
- Каждое wh, whc сжимается и подсчитывается коэффициент компрессии
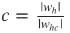 .
. - Это среднее распределяется по всем окнам — c∗.
- Рассчитывается ожидаемый коэффициент сжатия, используя псевдо-случайные данные — E[c∗].
- Если c∗>=min (1.0, E[c∗]), рынок не демонстрирует чрезмерную сжимаемость, что подразумевает его эффективность.
- Если c∗
Тест на R и разбор алгоритма
На R потребовалось не так чтобы очень много кода, чтобы сделать такой тест, поскольку в нем уже есть функции memCompress и memDecompress. Аналогичные функции есть и в Python.
compressionTest <- function(code, years = 7, algo = "g") {
# The generic Quandl API key for TuringFinance.
Quandl.api_key("t6Rn1d5N1W6Qt4jJq_zC")
# Download the raw price data.
data <- Quandl(code, rows = -1, type = "xts")
# Extract the variable we are interested in.
ix.ac <- which(colnames(data) == "Adjusted Close")
if (length(ix.ac) == 0)
ix.ac <- which(colnames(data) == "Close")
ix.rate <- which(colnames(data) == "Rate")
closes <- data[ ,max(ix.ac, ix.rate)]
# Get the month endpoints.
monthends <- endpoints(closes)
monthends <- monthends[2:length(monthends) - 1]
# Observed compression ratios.
cratios <- c()
for (t in ((12 * years) + 1):length(monthends)) {
# Extract a window of length equal to years.
window <- closes[monthends[t - (12 * years)]:monthends[t]]
# Compute detrended log returns.
returns <- Return.calculate(window, method = "log")
returns <- na.omit(returns) - mean(returns, na.rm = T)
# Binarize the returns.
returns[returns < 0] <- 0
returns[returns > 0] <- 1
# Convert into raw hexadecimal.
hexrets <- bin2rawhex(returns)
# Compute the compression ratio
cratios <- c(cratios, length(memCompress(hexrets)) /
length(hexrets))
}
# Expected compression ratios.
ecratios <- c()
for (i in 1:length(cratios)) {
# Generate some benchmark returns.
returns <- rnorm(252 * years)
# Binarize the returns.
returns[returns < 0] <- 0
returns[returns > 0] <- 1
# Convert into raw hexadecimal.
hexrets <- bin2rawhex(returns)
# Compute the compression ratio
ecratios <- c(ecratios, length(memCompress(hexrets)) /
length(hexrets))
}
if (mean(cratios) >= min(1.0, mean(ecratios))) {
print(paste("Dataset:", code, "is not compressible { c =",
mean(cratios), "} --> efficient."))
} else {
print(paste("Dataset:", code, "is compressible { c =",
mean(cratios), "} --> inefficient."))
}
}
bin2rawhex <- function(bindata) {
bindata <- as.numeric(as.vector(bindata))
lbindata <- split(bindata, ceiling(seq_along(bindata)/4))
hexdata <- as.vector(unlist(mclapply(lbindata, bin2hex)))
hexdata <- paste(hexdata, sep = "", collapse = "")
hexdata <- substring(hexdata,
seq(1, nchar(hexdata), 2),
seq(2, nchar(hexdata), 2))
return(as.raw(as.hexmode(hexdata)))
}
Код на GitHub
Далее представлено краткое описание трех компрессионных схем, которые используются в алгоритме сжатия.
- GZIP-сжатие. Основано на DEFLATE-алгоритме, который сочетает кодировку LZ1 и Huffman. LZ1 назван по имени Абрахама Лемпеля и Якоба Зива. Он работает методом замены повторяющихся паттернов в последовательности, расставляя ссылки на копии этих паттернов в изначальной несжатой версии. Каждое соответствие закодировано через длинную пару, содержащую следующую информацию для декодера: параметр y равен всем параметрам через расстояние x после него. Второй алгоритм назван по имени Дэвида Хаффмана, конструирует оптимальное префиксное дерево по частоте появлений паттернов в последовательности.
- BZIP2-сжатие. Использует три механизма компрессии: преобразование Барроуза-Уилера, преобразование движения к началу (MTF) и кодирование Хаффмана. Первый из них — это реверсивный метод для перегруппировки последовательности в поток похожих символов для упрощения процедуры сжатия стандартными методами. Преобразование MTF заменяет буквы в последовательности их индексами в стеке. Таким образом, длинная последовательность идентичных букв заменяется меньшим числом, редко встречающиеся буквы — большим.
- XZ-сжатие. Работает через последовательность алгоритмов Лемпель-Зив-Марков, которая была разработана в 7z формате сжатия. Это, по сути, словарный алгоритм сжатия, который следует за алгоритмом LZ1. Его вывод закодирован с использованием модели, которая осуществляет вероятностное предсказание каждого бита, называемой адаптивным бинарным кодировщиком диапазона.
Все три алгоритма, к примеру, доступны в языке R через функции memCompress и memDecompress. Единственная проблема с этими функциями — инпут должен быть дан в виде шестнадцатеричной последовательности. Для перевода можно использовать функцию bin2rawhex.
Результаты и их о (бес)смысленность
Для эксперимента использовался 51 глобальный рыночный индекс и 12 валютных пар. Последовательности были протестированы по недельной и суточной частоте.
Все активы были сжаты через алгоритмы gzip, bzip2, и xz с использованием методологии walk-forward. За исключением пары доллар/рубль, ни один из активов не продемонстрировал избыточную сжимаемость. По факту, ни один из них не показал никакой сжимаемости вообще. Эти результаты подтвердили выводы прошлого эксперимента с тестом линейной сложности. Но они противоречат результатам NIST тестов и результатам теста Ло-МакКинли. Осталось разобраться, почему.
Вариант 1. Первый вывод заключается в том, чтобы признать (на радость академикам), что мировые рынки относительно эффективны. Их поведение выглядит достаточно случайным.
Вариант 2. Или можно признать, что что-то определенно не в порядке с алгоритмами сжатия без потери данных в отношении проверки эффективности и случайности финансовых рынков.
Для проверки этих гипотез автору эксперимента пришлось разработать тест для проверки компрессионного теста.
Тестирование компрессионного теста
Противники гипотезы случайного блуждания, на самом деле, не настаивают на 100% детерминированности рынков. Речь о том, чтобы доказать, что поведение рынков не на 100% случайно. Иными словами у рынков есть две ипостаси: сигнал и шум. Сигнал проявляет себя в сотнях аномалий, а шум действует как очевидная случайность и эффективность. Это две стороны медали. Следующий шаг — признать, что шум, производимый системой, не отменяет действие сигналов. Остается возможность «взломать» рынок, находя и используя такие сигналы.
Исходя из вышеизложенного, автор предлагает следующую формулу для тестирования компрессионного теста:

Если мы увеличиваем размер стандартного отклонения компоненты шума — ϵt, мы наблюдаем, как сжимаемость рынка начинает ухудшаться. Когда стандартная девиация проходит отметку 0,01, компрессионный тест начинает сбоить:
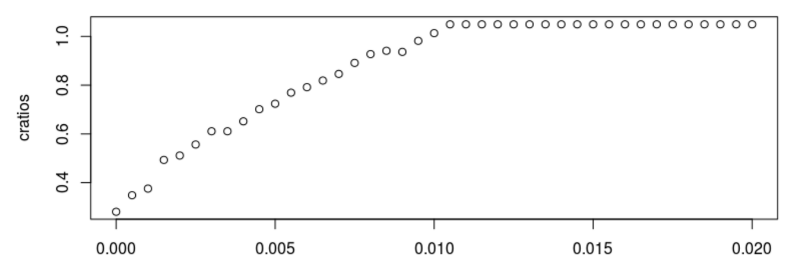
Примеры выводов в тесте для σ=0.010, σ=0.020 иσ=0.040 выглядят следующим образом:

В компрессионном тесте все эти рынки случайны или эффективны, потому что не могут быть сжаты через алгоритмы сжатия без потерь данных. Да, они могут казаться случайными. Но состоят-то они из сигналов и шума, поэтому случайность не может быть полной.
Для более адекватной проверки необходимо использовать ставочную стратегию/алгоритм возврата к среднему:
- Вывод: размер окна w=4;
- Для параметра времени t подсчитаем совокупный возврат к прошлым w-минус день t — c.
- Если с<0,0, удерживаем 100% актива (ставим на то, что актив пойдет вверх);
- В любом другом случае скидываем акции.
Ниже представлены две диаграммы для каждого уровня шума. На первой представлено 30 кривых акций, сгенерированных ставочной стратегией возврата к среднему. На второй показан средний доход рынка из предыдущего примера в сравнении с доходом от применения стратегии.

Это упрощенный пример, но он помогает выявить противоречие:
Если рынок не сжимаем, из этого следует, что он эффективный, но если бы он был по-настоящему эффективным, невозможно было бы применить к нему ставочную стратегию, которая его «взламывает».
Мы должны это «понять и простить», потому что случайность недоказуема, последовательность фактически не случайна. По мнению автора, компрессионный тест провалился потому, что он более чувствителен к шуму, чем трейдинговая стратегия (в симуляции он дает 10-кратную чувствительность к шуму). Причина может быть в использовании алгоритмов сжатия без потери данных.
Код для проверочного теста можно посмотреть здесь.
Выводы
В настоящем исследовании была представлена идея о том, как можно с помощью алгоритмов компрессии протестировать случайность рынков, и что это дает к пониманию их эффективности. Потом был запущен «метатест», который указал на высокую чувствительность подобных тестов к любому шуму. В итоге можно сделать несколько выводов:
- После проведения детрендинга рынок начинает демонстрировать достаточно шума и становится «непроходимым» для алгоритмов компрессии без потерь данных (gzip, bzip2, и xz).
- Если чувствительность теста к шуму оказывается выше, чем у трейдинговой стратегии (в примере статьи такой тест оказался в 10 раз чувствительней к шуму, чем простая ставочная стратегия), негативный результат еще не означает, что анализируемый рынок является эффективным. В том смысле, что его нельзя «взломать».
- Другими словами, такие тесты не доказывают правоту академиков, настаивающих на жесткой трактовке гипотезы случайного блуждания рынка. Просто все вышло сложнее, чем казалось на первый взгляд.
- Статистические тесты для определения случайности рынка различаются по размеру, охвату и чувствительности. Надежный результат способна дать лишь комбинация нескольких тестов.
Другие материалы по теме от ITinvest:
