[Перевод] Алгоритм Форчуна, подробности реализации22.11.2018 12:47

Последние несколько недель я работал над реализацией алгоритма Форчуна на C++. Этот алгоритм берёт множество 2D-точек и строит из них диаграмму Вороного. Если вы не знаете, что такое диаграмма Вороного, то взгляните на рисунок:

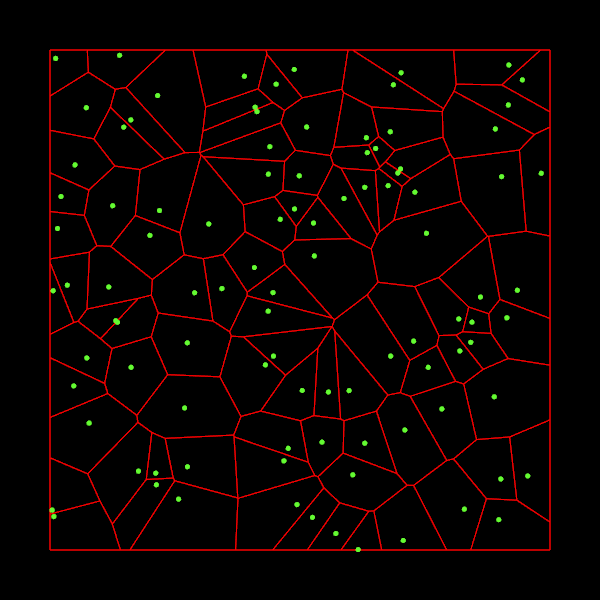
Для каждой входной точки, которая называется «местом» (site), нам нужно найти множество точек, которые ближе к этому месту, чем ко всем остальным. Такие множества точек образуют ячейки, которые показаны на изображении выше.

В алгоритме Форчуна примечательно то, что он строит такие диаграммы за время $O(n\log n)$ (что оптимально для использующего сравнения алгоритма), где $n$ — это количество мест.

Я пишу эту статью, потому что считаю реализацию этого алгоритма очень сложной задачей. На данный момент это самый сложный из алгоритмов, которые мне приходилось реализовывать. Поэтому я хочу поделиться теми проблемами, с которыми я столкнулся, и способами их решения.

Как обычно, код выложен на github, а все использованные мной справочные материалы перечислены в конце статьи.

Я не буду объяснять, как работает алгоритм, потому что с этим уже хорошо справились другие люди. Могу порекомендовать изучить эти две статьи: здесь и здесь. Вторая очень любопытна — автор написал интерактивное демо на Javascript, которое полезно для понимания работы алгоритма. Если вам нужен более формальный подход со всеми доказательствами, то рекомендую прочитать главу 7 книги Computational Geometry, 3rd edition.

Более того, я предпочитаю разбираться с подробностями реализации, которые задокументированы не так хорошо. И именно они делают реализацию алгоритма такой сложной. В особенности я сосредоточусь на использованных структурах данных.

Я только написал псевдокод алгоритма, чтобы вы получили понятие о его глобальной структуре:

добавляем событие места в очередь событий для каждого места
пока очередь событий не пуста
    извлекаем верхнее событие
    если событие является событием места
        вставляем в линию побережья новую дугу
        проверяем наличие новых событий окружностей
    иначе
        создаём в диаграмме вершину
        удаляем из береговой линии стянутую дугу
        удаляем недействительные события
        проверяем наличие новых событий окружностей

Первая проблема, с которой я столкнулся — выбор способа хранения диаграммы Вороного.

Я решил использовать структуру данных, широко применяемую в вычислительной геометрии, которая называется двусвязным списком рёбер (doubly connected edge list, DCEL).

Мой класс VoronoiDiagram использует в качестве полей четыре контейнера:

class VoronoiDiagram
{
public:
    // ...

private:
    std::vector mSites;
    std::vector mFaces;
    std::list mVertices;
    std::list mHalfEdges;
}

Я подробно расскажу о каждом из них.

Класс Site описывает входную точку. Каждое место имеет индекс, который полезен для занесения его в очередь, координаты и указатель на ячейку (face):

struct Site
{
    std::size_t index;
    Vector2 point;
    Face* face;
};

Вершины ячейки представлены классом Vertex, у них есть только поле координат:

struct Vertex
{
    Vector2 point;
};

Вот реализация полурёбер:

struct HalfEdge
{
    Vertex* origin;
    Vertex* destination;
    HalfEdge* twin;
    Face* incidentFace;
    HalfEdge* prev;
    HalfEdge* next;
};

Вы можете задаться вопросом — что такое полуребро? Ребро в диаграмме Вороного является общим для двух соседних ячеек. В структуре данных DCEL мы разделяем эти рёбра на два полуребра, по одному для каждой ячейки, и они связываются указателем twin. Более того, у полуребра есть исходная и конечная точки. Поле incidentFace указывает на грань, которой принадлежит полуребро. Ячейки в DCEL реализуются как циклический двусвязный список полурёбер, в котором соседние полурёбра соединены вместе. Поэтому поля prev и next указывают на предыдующие и следующие полурёбра в ячейке.

На рисунке ниже показаны все эти поля для красного полуребра:

Наконец, класс Face задаёт ячейку. Он просто содержит указатель на своё место и ещё один на одно из его полурёбер. Не важно, какое из полурёбер выбрано, потому что ячейка — это замкнутый полигон. Таким образом, мы получаем доступ ко всем полурёбрам при обходе циклического связанного списка.

struct Face
{
    Site* site;
    HalfEdge* outerComponent;
};

Стандартный способ реализации очереди событий — очередь с приоритетами. В процессе обработки событий места и окружностей нам может понадобиться удалить события окружностей из очереди, потому что они больше не являются действительными. Но большинство стандартных реализаций очереди с приоритетами не позволяют удалять элемент, не находящийся на вершине. В частности это относится и к std::priority_queue.

Эту проблему можно решить двумя способами. Первый, более простой — добавить к событиям флаг valid. Изначально valid имеет значение true. Тогда вместо удаления события окружности из очереди, мы можем просто присвоить его флагу значение false. Наконец, при обработке всех событий в основном цикле мы проверяем, равно ли значение флага valid события false, и если это так, то просто пропускаем его и обрабатываем следующее.

Второй способ, который применил я — не использовать std::priority_queue. Вместо неё я реализовал собственную очередь с приоритетами, которая поддерживает удаление любого содержащегося в ней элемента. Реализация такой очереди довольно проста. Я выбрал этот способ, потому что он делает код алгоритма чище.

Структура данных береговой линии — сложная часть алгоритма. В случае неверной реализации нет никаких гарантий, что алгоритм будет выполняться за $O(n\log n)$ . Ключ к получению такой временной сложности — использование самобалансирующегося дерева. Но это проще сказать, чем сделать!

В большинстве ресурсов, которые я изучал (две вышеупомянутые статьи и книга Computational Geometry), советуют реализовывать береговую линию как дерево, в котором внутренние узлы обозначают точки излома, а листья обозначают дуги. Но в них ничего не говорится о том, как сбалансировать дерево. Думаю, что такая модель не самая лучшая, и вот почему:

в ней есть избыточная информация: мы знаем, что между двумя соседними дугами есть точка излома, поэтому необязательно представлять эти точки в виде узлов
она неадекватна для самобалансировки: можно сбалансировать только поддерево, образованное точками излома. Мы и в самом деле не можем сбалансировать всё дерево целиком, потому что в противном случае дуги могут стать внутренними узлами и листьями точек излома. Написание алгоритма для балансировки только поддерева, образованного внутренними узлами, мне кажется кошмарной задачей.

Поэтому я решил представить береговую линию иначе. В моей реализации береговая линия тоже является деревом, но все узлы обозначают дуги. Такая модель не имеет ни одного из перечисленных недостатков.

Вот определение дуги Arc в моей реализации:

struct Arc
{
    enum class Color{RED, BLACK};

    // Hierarchy
    Arc* parent;
    Arc* left;
    Arc* right;
    // Diagram
    VoronoiDiagram::Site* site;
    VoronoiDiagram::HalfEdge* leftHalfEdge;
    VoronoiDiagram::HalfEdge* rightHalfEdge;
    Event* event;
    // Optimizations
    Arc* prev;
    Arc* next;
    // Only for balancing
    Color color;
};

Первые три поля используются для структуры дерева. Поле leftHalfEdge указывает на полуребро, отрисованное крайней левой точкой дуги. А rightHalfEdge — на полуребро, отрисованное крайней правой точкой. Два указателя, prev и next используются для получения прямого доступа к предыдущей и следующей дуге береговой линии. Кроме того, они также позволяют обойти береговую линию как двусвязанный список. И наконец, у каждой дуги есть цвет, который используется для балансировки береговой линии.

Для балансировки береговой линии я решил воспользоваться красно-чёрной схемой. При написании кода я вдохновлялся книгой Introduction to Algorithms. В главе 13 описаны два интересных алгоритма, insertFixup и deleteFixup, которые балансируют дерево после вставки или удаления.

Однако я не могу использовать приведённый в книге метод insert, потому что для нахождения места вставки узла в нём используются ключи. В алгоритме Форчуна нет ключей, мы только знаем, что нужно вставлять дугу до или после другой в береговой линии. Чтобы реализовать это, я создал методы insertBefore и insertAfter:

void Beachline::insertBefore(Arc* x, Arc* y)
{
    // Find the right place
    if (isNil(x->left))
    {
        x->left = y;
        y->parent = x;
    }
    else
    {
        x->prev->right = y;
        y->parent = x->prev;
    }
    // Set the pointers
    y->prev = x->prev;
    if (!isNil(y->prev))
        y->prev->next = y;
    y->next = x;
    x->prev = y;
    // Balance the tree
    insertFixup(y);    
}

Вставка y перед x выполняется в три этапа:

Находим место для вставки нового узла. Для этого я воспользовался следующим наблюдением: левый дочерний элемент x или правый дочерний элемент x->prev равен Nil, и тот из них, который равен Nil находится перед x и после x->prev.
Внутри береговой линии мы сохраняем структуру двусвязного списка, поэтому мы должны соответствующим образом обновлять указатели prev и next элементов x->prev, y и x.
Наконец, мы просто вызываем для балансировки дерева метод insertFixup, описанный в книге.

insertAfter реализуется аналогично.

Взятый из книги метод удаления можно реализовать без изменений.

Вот выходные данные описанного выше алгоритма Форчуна:

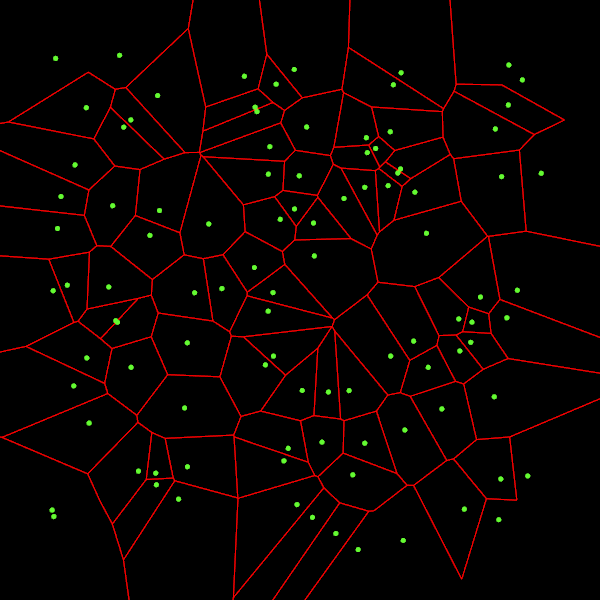
Возникает небольшая проблема с некоторыми рёбрами ячеек на границе изображения: они не отрисовываются, потому что они бесконечны.

Хуже того — ячейка может и не быть одним фрагментом. Например, если мы возьмём три точки, находящиеся на одной прямой, то у средней точки будет два бесконечных полуребра, не связанных вместе. Это не очень нас устраивает, потому что мы не сможем получить доступ к одному из полурёбер, ведь ячейка является связанным списком рёбер.

Чтобы решить эти проблемы, мы ограничим диаграмму. Под этим я подразумеваю то, что мы ограничим каждую ячейку диаграммы, чтобы в них больше не было бесконечных рёбер и каждая ячейка являлась замкнутым полигоном.

К счастью, алгоритм Форчуна позволяет нам быстро найти бесконечные рёбра: они соответствуют полурёбрам, всё ещё находящимся в береговой линии к концу работы алгоритма.

Мой алгоритм ограничения получает в качестве входных данных прямоугольник (box) и состоит из трёх этапов:

Он обеспечивает размещение каждой вершины диаграммы внутри прямоугольника.
Отсекает каждое бесконечное ребро.
Замыкает ячейки.

Этап 1 тривиален — нам просто нужно расширить прямоугольник, если он не содержит вершину.

Этап 2 тоже довольно прост — он состоит из вычисления пересечений между лучами и прямоугольником.

Этап 3 также не очень сложен, только требует внимательности. Я выполняю его в два этапа. Сначала я добавляю точки углов прямоугольника к ячейкам, в вершинах которых они должны быть. Затем я делаю так, чтобы все вершины ячейки были соединены полурёбрами.

Рекомендую изучить код и задать вопросы, если вам нужны подробности об этой части.

Вот выходная диаграмма ограничивающего алгоритма:

Теперь мы видим, что все рёбра отрисовываются. И если уменьшить масштаб, то можно убедиться, что все ячейки замкнуты:

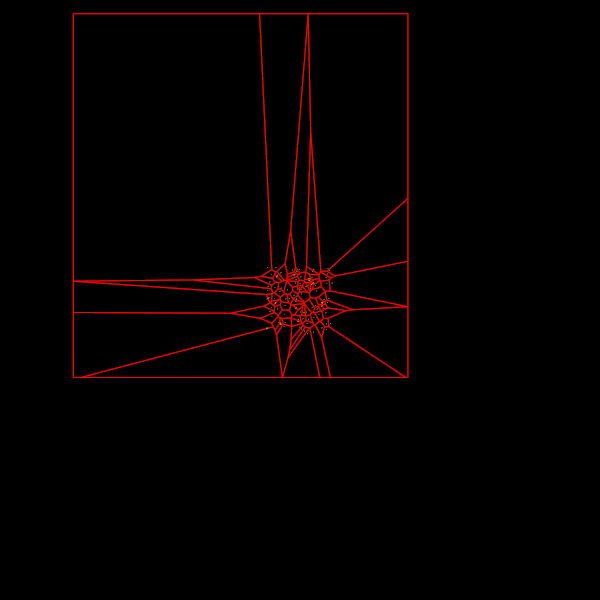
Отлично! Но первое изображение из начала статьи лучше, правда?

Во многих случаях применения полезно иметь пересечение между диаграммой Вороного и прямоугольником, как и показано на первом изображении.

Хорошо то, что после ограничения диаграммы сделать это гораздо проще. Плохо то, что хоть алгоритм и не очень сложен, нам нужно быть внимательными.

Идея заключается в следующем: мы обходим её полурёбра каждой ячейки и проверяем пересечение между полуребром и прямоугольником. Возможны пять случаев:

Полуребро полностью находится внутри прямоугольника: такое полуребро мы сохраняем
Полуребро полностью находится снаружи прямоугольника: такое полуребро мы отбрасываем
Полуребро выходит наружу прямоугольника: мы усекаем полуребро и сохраняем его как последнее полуребро, выходившее наружу.
Полуребро входит внутрь прямоугольника: мы усекаем полуребро, чтобы связать его с последним полуребром, выходившим наружу (мы сохраняем его в случае 3 или 5)
Полуребро пересекает прямоугольник дважды: мы усекаем полуребро и добавляем полурёбра, чтобы связать ег с последним полуребром, выходившим наружу, а затем сохраняем его как новое последнее полуребро, выходившее наружу.

Да, получилось много случаев. Я создал картинку, чтобы все их показать:

Оранжевый полигон — это исходная ячейка, а красный — усечённая ячейка. Усечённые полурёбра обозначены красным. Зелёные рёбра добавлены, чтобы связать полурёбра, входящие в прямоугольник, с полурёбрами, выходящими наружу.

Применив этот алгоритм к ограниченной диаграмме, мы получаем ожидаемый результат:

Статья оказалась довольно длинной. И я уверен, что многие аспекты до сих пор вам непонятны. Тем не менее, надеюсь, она будет вам полезной. Изучите код, чтобы разобраться в подробностях.

Чтобы подвести итог и убедиться, что мы не потратили время зря, я измерил на своём (дешёвом) ноутбуке время вычисления диаграммы Вороного для разного количества мест:

: 2 мс
: 33 мс
: 450 мс
: 6600 мс

Мне не с чем сравнить эти показатели, но кажется, что это невероятно быстро!