[Перевод] Алгоритм быстрого и простого объёмного рендеринга11.05.2020 17:37

Недавно я написал небольшой ShaderToy, выполняющий простой объёмный рендеринг, а затем решил опубликовать пост с объяснением его работы. Сам интерактивный ShaderToy можно посмотреть здесь. Если вы читаете с телефона или ноутбука, то рекомендую посмотреть эту быструю версию. Я включил в пост фрагменты кода, которые помогут вам понять работу ShaderToy на высоком уровне, но в них есть не все подробности. Если вы хотите разобраться глубже, то рекомендую сверяться с кодом ShaderToy.

У моего ShaderToy были три основные задачи:

Выполнение в реальном времени
Простота
Физическая корректность (… или типа того)

Я начну с этой сцены с кодом-заготовкой. Не буду вдаваться в подробности реализации, потому что она не очень интересна, но вкратце расскажу, с чего мы начинаем:

Трассировка лучей непрозрачных объектов. Все объекты являются примитивами с простыми пересечениями с лучами (1 плоскость и 3 сферы)
Для вычисления освещения используется затенение по Фонгу, а в трёх сферических источниках света применется настраиваемый коэффициент затухания света. Лучи теней не требуются, потому что мы освещаем только плоскость.

Вот как это выглядит:

Мы будем рендерить объём как отдельный проход, который смешивается с непрозрачной сценой; это похоже на то, как все движки рендеринга реального времени по отдельности обрабатывают непрозрачные и просвечивающие поверхности.
Но сначала, прежде чем мы сможем приступить к объёмному рендерингу, нам нужен этот самый объём! Для моделирования объёма я решил использовать функции расстояний со знаком (signed distance functions, SDF). Почему именно функции полей расстояний? Потому что я не художник, а они позволяют создавать очень органичные формы всего в нескольких строках кода. Я не буду подробно рассказывать о функциях расстояний со знаком, потому что Иниго Килес уже замечательно их объяснил. Если вам любопытно, то здесь есть отличный список различных фунций расстояний со знаком и модификаторов. А вот ещё одна статья о raymarching этих SDF.

Давайте начнём с простого и добавим сюда сферу:

Теперь мы добавим ещё одну сферу и используем плавное сопряжение для слияния функций расстояний сфер. Этот я код взял прямиком со страницы Иниго, но для понятности вставлю его сюда:

// Taken from https://iquilezles.org/www/articles/distfunctions/distfunctions.htm
float sdSmoothUnion( float d1, float d2, float k ) 
{
    float h = clamp( 0.5 + 0.5*(d2-d1)/k, 0.0, 1.0 );
    return mix( d2, d1, h ) - k*h*(1.0-h); 
}

Плавное сопряжение — чрезвычайно мощный инструмент, потому что можно получить нечто довольно интересное, просто скомбинировав его с несколькими простыми фигурами. Вот как выглядит моё множество сфер с плавным сопряжением:

Итак, у нас получилось нечто каплевидное, но нам нужно что-то больше похожее на облако, чем на каплю. Замечательное свойство SDF заключается в том, насколько легко исказить поверхность, просто добавив к SDF немного шума. Поэтому давайте добавим поверх немного шума дробного броуновского движения (fractal brownian motion, fBM), используя позицию для индексирования функции шума. Иниго Килес тоже раскрыл эту тему в замечательной статье о fBM-шуме. Вот как будет выглядеть изображение с наложенным поверх fBM-шумом:

Отлично! Благодаря fBM-шуму объект внезапно стал выглядеть намного интереснее!

Теперь нам нужно создать иллюзию того, что объём взаимодействует плоскостью земли. Для этого я добавил немного ниже плоскости земли расстояние плоскости со знаком и заново использовал объединение плавного сопряжения с очень агрессивным значением сопряжения (параметр k). После этого мы получили вот такую картину:

Финальным штрихом будет изменение индекса xz fBM-шума со временем, чтобы объём имел вид клубящегося тумана. В движении это выглядит очень хорошо!

Отлично, у нас получилось нечто, напоминающее облако! Код вычисления SDF тоже довольно компактен:

float QueryVolumetricDistanceField( in vec3 pos)
{    
    vec3 fbmCoord = (pos + 2.0 * vec3(iTime, 0.0, iTime)) / 1.5f;
    float sdfValue = sdSphere(pos, vec3(-8.0, 2.0 + 20.0 * sin(iTime), -1), 5.6);
    sdfValue = sdSmoothUnion(sdfValue,sdSphere(pos, vec3(8.0, 8.0 + 12.0 * cos(iTime), 3), 5.6), 3.0f);
    sdfValue = sdSmoothUnion(sdfValue, sdSphere(pos, vec3(5.0 * sin(iTime), 3.0, 0), 8.0), 3.0) + 7.0 * fbm_4(fbmCoord / 3.2);
    sdfValue = sdSmoothUnion(sdfValue, sdPlane(pos + vec3(0, 0.4, 0)), 22.0);
    return sdfValue;
}

Это просто рендеринг непрозрачного объекта. Нам же нужен красивый пышный туман!

Как же нам отрендерить его в виде объёма, а не непрозрачного объекта? Давайте сначала поговорим о симулируемой нами физике. Объём представляет собой огромное количество частиц в определённой области пространства. И когда я говорю «огромное», то имею в виду «ОГРОМНОЕ». Настолько, что моделирование каждой из этих частиц сегодня является нереализуемой задачей, даже для офлайн-рендеринга. Хорошими примерами этого являются огонь, туман и облака. Строго говоря, всё является объёмом, но ради скорости вычислений легче закрыть на это глаза и притвориться, что это не так. Мы представляем скопление этих частиц как значения плотности, обычно хранящиеся в какой-нибудь 3D-сетке (или чём-то более сложном, например, в OpenVDB).

Когда свет проходит сквозь объём, то при столкновении света с частицей может произойти пара явлений. Он может или рассеяться и пойти в другом направлении, или часть света может быть поглощена частицей и раствориться. Чтобы соблюдать требование выполнения в реальном времени, мы будем выполнять то, что называется одиночным рассеянием. Это означает следующее: мы будем считать, что свет рассеивается только один раз, когда свет сталкивается с частицей и летит в сторону камеры. То есть мы не сможем симулировать эффекты многократного рассеивания, например, тумана, в котором объекты на удалении обычно выглядят более расплывчатыми. Но для нашей системы этого вполне достаточно. Вот как выглядит одиночное рассеяние (single scattering) при raymarching:

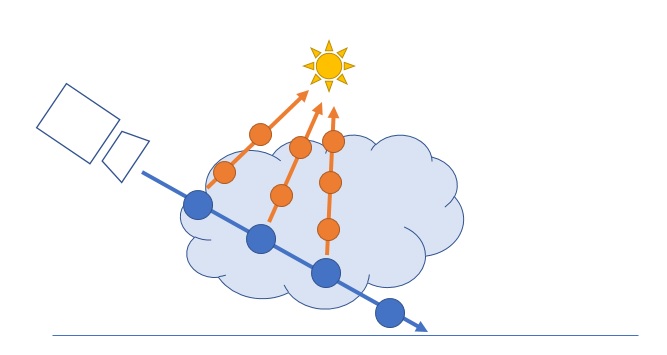
Псевдокод для него выглядит примерно так:

for n steps along the camera ray:
   Calculate what % of your ray hit particles (i.e. were absorbed) and needs lighting
   for m lights:
      for k steps towards the light:
         Calculate % of light that were absorbe in this step
      Calculate lighting based on how much light is visible
Blend results on top of opaque objects pass based on % of your ray that made it through the volume

То есть мы имеем дело с вычислениями со сложностью O (n * m * k). Так что GPU придётся потрудиться.

Вычисляем поглощение

Давайте сначала разберёмся с поглощением света в объёме вдоль луча камеры (т.е. давайте пока не будем выполнять raymarching в направлении источников освещения). Для этого нам нужно два действия:

Выполнить raymarching внутри объёма
Вычислить поглощение/освещение на каждом шаге

Чтобы вычислить, сколько света поглощается в каждой точек, мы используем закон Бугера — Ламберта — Бера, описывающий ослабление света при прохождении через материал. Вычисления на удивление просты:

float BeerLambert(float absorptionCoefficient, float distanceTraveled)
{
    return exp(-absorptionCoefficient * distanceTraveled);
}

Коэффициент absorptionCoefficient — это параметр материала. Например, в прозрачном объёме, например, в воде, это значение будет низким, а у чего-то более густого, например, молока, коэффициент будет более высоким.

Чтобы выполнить raymarching объёма, мы просто делаем шаги фиксированного размера вдоль луча и получаем поглощение на каждом шаге. Возможно, вам непонятно, зачем делать фиксированные шаги вместо чего-то более быстрого, например, трассировки сферы, но если вспомнить, что плотность в пределах объёма неоднородна, то всё становится понятным. Ниже показан код raymarching и накопления поглощения. Некоторые переменные находятся вне пределов этого фрагмента кода, так что посмотрите полную реализацию в ShaderToy.

float opaqueVisiblity = 1.0f;
const float marchSize = 0.6f;
for(int i = 0; i < MAX_VOLUME_MARCH_STEPS; i++) {
	volumeDepth += marchSize;
	if(volumeDepth > opaqueDepth) break;
	
	vec3 position = rayOrigin + volumeDepth*rayDirection;
	bool isInVolume = QueryVolumetricDistanceField(position) < 0.0f;
	if(isInVolume) 	{
		float previousOpaqueVisiblity = opaqueVisiblity;
		opaqueVisiblity *= BeerLambert(ABSORPTION_COEFFICIENT, marchSize);
		float absorptionFromMarch = previousOpaqueVisiblity - opaqueVisiblity;
		for(int lightIndex = 0; lightIndex < NUM_LIGHTS; lightIndex++) {
			float lightDistance = length((GetLight(lightIndex).Position - position));
			vec3 lightColor = GetLight(lightIndex).LightColor * GetLightAttenuation(lightDistance);  
			volumetricColor += absorptionFromMarch * volumeAlbedo * lightColor;
		}
		volumetricColor += absorptionFromMarch * volumeAlbedo * GetAmbientLight();
	}
}

И вот что мы при этом получим:

Похоже на сахарную вату! Возможно, для некоторых эффектов этого будет достаточно! Но нам не хватает самозатенения. Свет достигает всех частей объёма одинаково. Но это не физически корректно, в зависимости от величины объёма между рендерящейся точкой и источником освещения, мы будем получать разное количество поступающего света.

Самозатенение

Мы уже сделали самое сложное. Нам нужно сделать то же самое, что мы делали для вычисления поглощения вдоль луча камеры, но только вдоль луча света. Код вычисления величины света, достигающей каждой точки, по сути будет повторением кода, но дублировать его проще, чем хакать HLSL, чтобы получить нужную нам рекурсию. Поэтому вот как это будет выглядеть:

float GetLightVisiblity(in vec3 rayOrigin, in vec3 rayDirection, in float maxT, in int maxSteps, in float marchSize) {
    float t = 0.0f;
    float lightVisiblity = 1.0f;
    for(int i = 0; i < maxSteps; i++) {                       
        t += marchSize;
        if(t > maxT) break;

        vec3 position = rayOrigin + t*rayDirection;
        if(QueryVolumetricDistanceField(position) < 0.0) {
            lightVisiblity *= BeerLambert(ABSORPTION_COEFFICIENT, marchSize);
        }
    }
    return lightVisiblity;
}

Добавление самозатенения даёт нам следующее:

Смягчаем края

В данный момент мне уже вполне нравится наш объём. Я показал его талантливому руководителю VFX-отдела The Coalition Джеймсу Шарпу. Он сразу же заметил, что края объёма выглядят слишком резкими. И это совершенно верно — объекты наподобие облаков постоянно рассеиваются в окружающем их пространстве, поэтому их края смешиваются с пустым пространством вокруг объёма, что должно приводить к созданию очень плавных краёв. Джеймс предложил мне отличную идею — снижать плотность в зависимости от того, как близко мы находимся к краю. А поскольку мы работаем с функциями расстояний со знаком, реализовать это очень просто! Так что давайте добавим функцию, которую можно будет использовать для запроса плотности в любой точке объёма:

float GetFogDensity(vec3 position)
{   
    float sdfValue = QueryVolumetricDistanceField(position)
    const float maxSDFMultiplier = 1.0;
    bool insideSDF = sdfDistance < 0.0;
    float sdfMultiplier = insideSDF ? min(abs(sdfDistance), maxSDFMultiplier) : 0.0;
    return sdfMultiplier;
}

А затем мы просто свернём его в значение поглощения:

opaqueVisiblity *= BeerLambert(ABSORPTION_COEFFICIENT * GetFogDensity(position), marchSize);

И вот как это выглядит:

Функция плотности

Теперь, когда у нас есть функция плотности, можно легко добавить в объём немного шума для придания ему дополнительных деталей и пышности. В данном случае я просто повторно использую функцию fBM, которую мы применяли для настройки формы объёма.

float GetFogDensity(vec3 position)
{   
    float sdfValue = QueryVolumetricDistanceField(position)
    const float maxSDFMultiplier = 1.0;
    bool insideSDF = sdfDistance < 0.0;
    float sdfMultiplier = insideSDF ? min(abs(sdfDistance), maxSDFMultiplier) : 0.0;
   return sdfMultiplier * abs(fbm_4(position / 6.0) + 0.5);
}

И так мы получили следующее:

Непрозрачное самозатенение

Объём уже выглядит довольно красиво! Но через него по-прежнему просачивается немного света. Здесь мы видим, как зелёный цвет просачивается там, где объём точно должен его поглощать:

Так получается, потому что непрозрачные объекты рендерятся до рендеринга объёма, так что они не принимают во внимание затенение, вызываемое объёмом. Это довольно просто исправить — у нас есть функция GetLightVisiblity, которую можно использовать для вычисления затенения, так что нам просто нужно вызвать её для освещения непрозрачного объекта. Мы получаем следующее:

Кроме создания красивых разноцветных теней это помогает улучшить тени и встроить объём в сцену. Кроме того, благодаря плавным краям объёма мы получаем мягкие тени, несмотря на то, что, строго говоря, работаем с точечными источниками освещения. Вот и всё! Здесь можно сделать ещё многое, но мне кажется, что я достиг нужного мне визуального качества, сохранив при этом относительную простоту примера.
Под конец я вкратце перечислю некоторые возможные оптимизации:

Перед выполнение raymarching по направлению к источнику освещения, нужно проверять по величине угасания света, действительно ли значимое количество этого света достигает рассматриваемой точки. В своей реализации я смотрю на яркость света, умноженную на albedo материала, и убеждаюсь, что значение достаточно велико для необходимости выполнения raymarching.
Если почти весь свет был поглощён объёмом, то нужно прекращать вычисления заранее, не тратя время на raymarching без видимых результатов
Отложить освещение непрозрачных объектов на момент после выполнения raymarching объёма. Если весь свет был поглощён объёмом, то мы можем пропустить вычисление освещения непрозрачных объектов. Однако нам всё равно нужно будет сначала вычислять глубину непрозрачных объектов, поэтому мы можем предварительно отказаться от raymarching объёма, если столкнёмся с непрозрачным объектом.

Вот и всё! Лично я был удивлён, что можно создать нечто довольно физически корректное в таком небольшом объёме кода (около 500 строк). Благодарю за прочтение, надеюсь, это было интересно.

И ещё одно замечание: вот забавное изменение — я добавил испускание света на основании расстояния SDF, чтобы создать эффект взрыва. Ведь взрывов никогда не бывает много.