[Перевод] AI, практический курс. Базовая модель распознавания эмоций на изображениях

В этой статье мы займемся построением базовой модели сверточной нейросети, которая способна выполнять распознавание эмоций на изображениях. Распознавание эмоций в нашем случаем представляет собой задачу двоичной классификации, целью которой является разделение изображений на позитивные и негативные.
Весь код, документы в формате notebook и прочие материалы, включая Dockerfile, можно найти здесь.
Данные
Первым действием практически во всех задачах машинного обучения должно быть понимание данных. Давайте сделаем это.
Структура набора данных
Сырые данные можно загрузить здесь (в документе Baseline.ipynb все действия данного раздела выполняются автоматически). Исходно данные находятся в архиве формата Zip*. Распакуем его и ознакомимся со структурой полученных файлов.
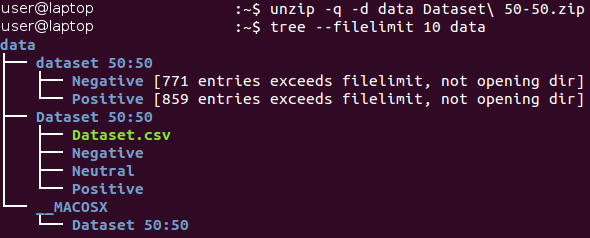
Все изображения хранятся внутри каталога «dataset 50:50» и распределены между двумя его подкаталогами, имя которых соответствует их классу — Negative (Негативные) и Positive (Позитивные). Обратите внимание на то, что задача немного несбалансирована — 53 процента изображений являются позитивными, и только 47 процентов — негативными. Обычно данные в задачах по классификации считаются несбалансированными, если количество примеров в различных классах различается очень значительно. Существует ряд способов работы с несбалансированными данными — например, субдискретизация, передискретизация, изменение весовых коэффициентов данных и т. д. В нашем случае несбалансированность имеет незначительный характер и не должна кардинально повлиять на процесс обучения. Необходимо лишь помнить о том, что наивный классификатор, всегда выдающий значение «позитивный», обеспечит значение точности примерно в 53 процента для этого набора данных.
Давайте посмотрим на несколько изображений каждого класса.
Отрицательные



Положительные



На первый взгляд изображения из разных классов на самом деле отличаются друг от друга. Однако давайте проведем более глубокое исследование и попробуем найти плохие примеры — похожие изображения, принадлежащие различным классам.
Например, у нас есть около 90 изображений змей, помеченных как негативные и около 40 очень похожих изображений змей, помеченных как позитивные.
Позитивное изображение змеи

Негативное изображение змеи

Такая же двойственность имеет место с пауками (130 негативных и 20 позитивных изображений), обнаженными людьми (15 негативных и 45 позитивных изображений) и некоторыми другими классами. Складывается ощущение, что маркировка изображений выполнялась разными людьми, и восприятие ими одинакового изображения может отличаться. Поэтому маркировка содержит присущую ей несогласованность. Эти два изображения змей практически идентичны, при этом разные эксперты отнесли их к различным классам. Таким образом можно сделать вывод, что едва ли возможно обеспечить 100-процентную точность при работе с данной задачей вследствие ее природы. Мы считаем, что более реалистичной оценкой точности будет значение в 80 процентов — эта величина основана на доле похожих изображений, обнаруженных в различных классах во время предварительной визуальной проверки.
Разделение процесса обучения/проверки
Мы всегда стремимся создать как можно более лучшую модель. Однако какой смысл мы вкладываем в это понятие? Существует множество различных критериев для этого, таких как: качество, время выполнения (обучение + получение вывода) и потребление памяти. Некоторые из них можно легко и объективно измерить (например, время и объем памяти), в то время как другие (качество) гораздо труднее поддаются определению. Например, ваша модель может демонстрировать 100-процентную точность при обучении на примерах, которые использовались для этого много раз, однако при этом потерпеть неудачу при работе с новыми примерами. Данная проблема называется сверхподгонкой и является одной из важнейших в машинном обучении. Также существует и проблема недоподгонки: в этом случае модель не может обучиться на основании представленных данных и демонстрирует плохие предсказания даже при использовании фиксированного обучающего набора данных.
Для решения проблемы сверхподгонки используется так называемая техника удерживания части образцов. Ее основная идея заключается в разбиении исходных данных на две части:
- Обучающий набор, который обычно составляет большую часть набора данных и используется для обучения модели.
- Проверочный набор обычно представляет собой небольшую часть исходных данных, которые разбиваются на две части перед выполнением всех процедур обучения. Данное множество вообще не используется при обучении и рассматривается в качестве новых примеров для тестирования модели после завершения обучения.
Используя данный метод, мы можем наблюдать, насколько хорошо наша модель обобщается (то есть работает с ранее неизвестными примерами).
В данной статье будет использоваться отношение размеров для обучающего и проверочного наборов, равное 4/1. Еще одним приемом, используемым нами, является так называемая стратификация. Данный термин обозначает разбиение каждого класса независимо от всех других классов. Такой подход позволяет поддерживать такую же сбалансированность между размерами классов в обучающем и проверочном наборах. Стратификация неявно использует предположение, что распределение примеров не изменяется при смене исходных данных и остается прежним при использовании новых примеров.
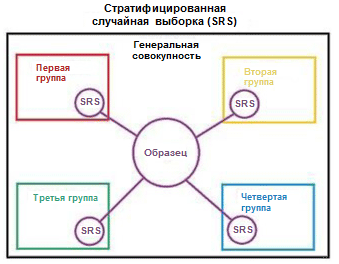
Проиллюстрируем понятие стратификации с помощью простого примера. Предположим, что у нас есть четыре группы/класса данных с соответствующим количеством объектов в них: дети (5), подростки (10), взрослые (80) и пожилые люди (5); см. рисунок справа (из Википедии). Теперь нам требуется разбить эти данные на два набора образцов в соотношении 3/2. При использовании стратификации примеров отбор объектов будет производиться независимо из каждой группы: 2 объекта из группы детей, 4 объекта из группы подростков, 32 объекта из группы взрослых и 2 объекта из группы пожилых людей. Новый набор данных содержит 40 объектов, что в точности составляет 2/5 от исходных данных. В то же самое время сбалансированность между классами в новом наборе данных соответствует их сбалансированности в исходных данных.
Все вышеописанные действия реализуются в одной функции, которая называется prepare_data; данную функцию можно найти в Python-файле utils.py. Эта функция загружает данные, разбивает их на обучающий и проверочный наборы с помощью фиксированного случайного числа (для последующего воспроизведения), после чего распределяет данные соответствующим образом между каталогами на жестком диске для последующего использования.
Предварительная обработка и аугментация
В одной из предыдущих статей были описаны действия по предварительной обработке и возможные причины для их использования в виде аугментации данных. Сверточные нейронные сети являются довольно сложными моделями, и для их обучения требуются большие объемы данных. В нашем случае имеется только 1600 примеров — этого, конечно, недостаточно.
Поэтому мы хотим расширить набор используемых данных с помощью аугментации данных. В соответствии с информацией, изложенной в статье о предварительной обработке данных, библиотека Keras* предоставляет возможность для аугментации данных «на лету» при чтении их с жесткого диска. Это можно сделать посредством класса ImageDataGenerator.
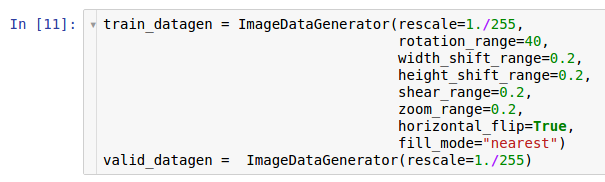
Здесь создаются два экземпляра генераторов. Первый экземпляр предназначен для обучения и использует множество случайных преобразований — таких как поворот, сдвиг, свертка, масштабирование и горизонтальный поворот — во время чтения данных с диска и передачи их в модель. Вследствие этого модель получает уже преобразованные примеры, и каждый полученный моделью пример является уникальным благодаря случайной природе этого преобразования. Второй экземпляр предназначен для проверки, и он лишь изменяет масштаб изображений. Обучающий и проверочный генераторы имеют только одно общее преобразование — изменение масштаба. Чтобы обеспечить вычислительную устойчивость модели, необходимо использовать для данных диапазон [0; 1] вместо [0; 255].
Архитектура модели
После изучения и подготовки исходных данных следует этап создания модели. Поскольку нам доступен небольшой объем данных, то мы собираемся построить сравнительно простую модель, чтобы иметь возможность обучить ее соответствующим образом и исключить ситуацию сверхподгонки. Давайте попробуем архитектуру стиля VGG, однако используем при этом меньшее количество слоев и фильтров.
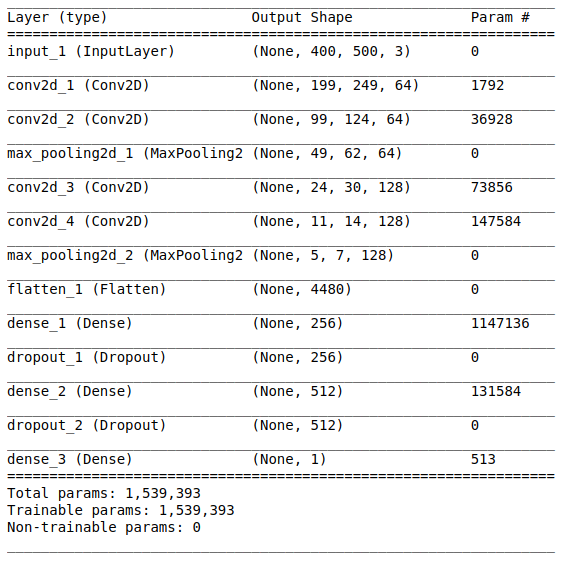

Архитектура сети состоит из следующих частей:
[Сверточный слой + сверточный слой + выбор максимального значения] × 2
Первая часть содержит два наложенных сверточных слоя с 64 фильтрами (с размером 3 и шагом 2) и слой для выбора максимального значения (с размером 2 и шагом 2), расположенный после них. Данная часть также обычно называется блоком выделения признаков, поскольку фильтры эффективно выделяют значимые признаки из входных данных (см. статью Обзор сверточных нейронных сетей для классификации изображений для получения дополнительной информации).
Выравнивание
Данная часть является обязательной, поскольку на выходе сверточной части получаются четырехмерные тензоры (примеры, высота, ширина и каналы). Однако для обычного полносвязного слоя нам требуется двухмерный тензор (примеры, признаки) в качестве входных данных. Поэтому необходимо выровнять тензор вокруг трех последних осей, чтобы объединить их в одну ось. Фактически это означает, что мы рассматриваем каждую точку в каждой карте признаков как отдельное свойство и выравниваем их в один вектор. На рисунке ниже представлен пример изображения размером 4 × 4 со 128 каналами, который выровнен в один протяженный вектор длиной в 1024 элемента.
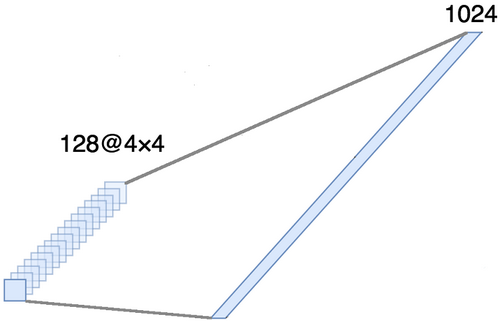
[Полносвязный слой + метод исключения] × 2
Перед вами классификационная часть сети. Она принимает выровненное представление признаков изображений и пытается классифицировать их наилучшим возможным образом. Данная часть сети состоит из двух наложенных блоков, состоящих из полносвязного слоя и метода исключения. Мы уже познакомились с полносвязными слоями — обычно это слои с полносвязным подключением. Но что такое «метод исключения»? Метод исключения — это техника регуляризации, позволяющая предотвратить сверхподгонку. Одним из возможных признаков сверхподгонки являются чрезвычайно различные значения весовых коэффициентов (порядки соответствующих величин). Существует множество способов решения данной задачи, включая уменьшение весов и метод исключения. Идея метода исключения заключается в отключении случайных нейронов во время обучения (список отключенных нейронов должен обновляться после каждого пакета/эпохи обучения). Это очень сильно препятствует получению совершенно различных значений для весовых коэффициентов — таким образом выполняется регуляризация сети.
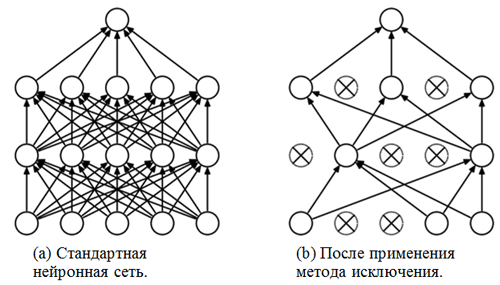
Пример применения метода исключения (рисунок взят из статьи Метод исключения: простой способ предотвратить сверхподгонку в нейронных сетях):
Сигмоидный модуль
Выходной слой должен соответствовать постановке задачи. В данном случае мы имеем дело с задачей двоичной классификации, поэтому нам требуется один выходной нейрон с сигмоидной функцией активации, которая оценивает вероятность P принадлежности к классу с номером 1 (в нашем случае это будут позитивные изображения). Тогда вероятность принадлежности к классу с номером 0 (негативные изображения) можно легко рассчитать как 1 — P.
Настройки и параметры обучения
Мы выбрали архитектуру модели и указали ее с помощью библиотеки Keras для языка Python. Кроме этого, перед началом обучения модели необходимо скомпилировать ее.

На этапе компиляции выполняется настройка модели для обучения. При этом необходимо указать три основных параметра:
- Оптимизатор. В данном случае мы используем оптимизатор по умолчанию Adam*, представляющий собой вид алгоритма стохастического градиентного спуска с моментом и адаптивной скоростью обучения (для получения дополнительной информации см. запись в блоге С. Рудера Обзор алгоритмов оптимизации градиентного спуска).
- Функция потери. Наша задача представляет собой проблему двоичной классификации, поэтому уместно будет использовать binary cross entropy в качестве функции потери.
- Метрики. Это опциональный аргумент, с помощью которого можно указать дополнительные метрики для отслеживания во время проведения процедуры обучения. В данном случае нам нужно отслеживать точность наряду с целевой функцией.
Теперь мы готовы к обучению модели. Обратите внимание, что процедура обучения выполняется с использованием генераторов, инициализированных в предыдущем разделе.
Число эпох представляет собой еще один гиперпараметр, который можно настроить. Здесь мы просто присваиваем ему значение 10. Также мы хотим сохранить модель и историю обучения, чтобы иметь возможность загрузить ее впоследствии.

Оценка
Теперь давайте посмотрим, насколько хорошо работает наша модель. Прежде всего рассмотрим изменение метрик в процессе обучения.
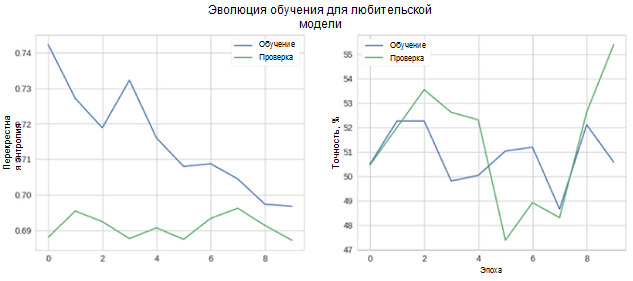
На рисунке можно видеть, что перекрестная энтропия проверки и точность не уменьшаются с течением времени. Более того, метрика точности для обучающего и проверочного набора просто колеблется около значения случайного классификатора. Итоговое значение точности для проверочного набора составляет 55 процентов, что лишь немногим лучше случайной оценки.
Давайте рассмотрим, как предсказания модели распределяются между классами. Для этой цели необходимо создать и визуализировать матрицу неточностей с помощью соответствующей функции из пакета Sklearn* для языка Python.
Каждая ячейка в матрице неточностей имеет свое собственное название:
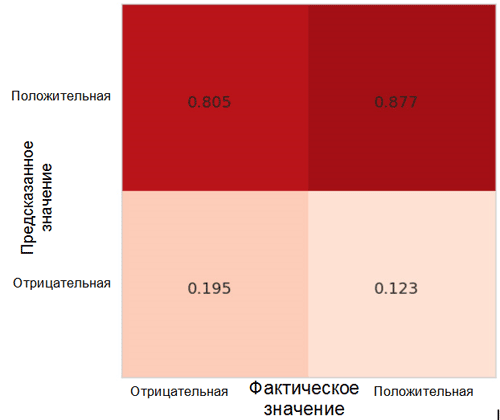
- True Positive Rate = TPR (верхняя правая ячейка) представляет собой долю позитивных примеров (класс 1, то есть позитивные эмоции в нашем случае), классифицированных правильным образом как позитивные.
- False Positive Rate = FPR (нижняя правая ячейка) представляет собой долю позитивных примеров, классифицированных неправильным образом как негативные (класс 0, то есть негативные эмоции).
- True Negative Rate = TNR (нижняя левая ячейка) представляет собой долю негативных примеров, классифицированных правильным образом как негативные.
- False Negative Rate = FNR (верхняя левая ячейка) представляет собой долю негативных примеров, классифицированных неправильным образом как позитивные.
В нашем случае оба значения TPR и FPR близки к 1. Это означает, что почти все объекты были классифицированы как позитивные. Таким образом, наша модель недалеко ушла от наивной базовой модели с постоянными предсказаниями большего по размеру класса (в нашем случае это позитивные изображения).
Еще одной интересной метрикой, за которой интересно наблюдать, является кривая рабочей характеристики приемника (ROC-кривая) и площадь под этой кривой (ROC AUC). Формальное определение этих понятий можно найти здесь. В двух словах, кривая ROC показывает, насколько хорошо работает двоичный классификатор.
Классификатор нашей сверточной нейросети имеет сигмоидный модуль в качестве выхода, который присваивает вероятность примера к классу 1. Теперь предположим, что наш классификатор демонстрирует хорошую работу и присваивает низкие значения вероятности для примеров класса 0 (гистограмма зеленого цвета на нижеприведенном рисунке) высокие значения вероятности для примеров класса 1 (гистограмма синего цвета).
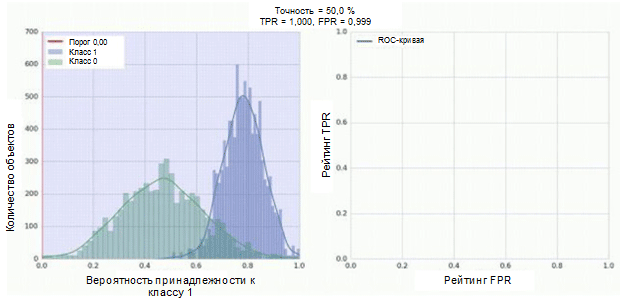
ROC-кривая демонстрирует, каким образом показатель TPR зависит от показателя FPR при перемещении порога классификации от 0 к 1 (правый рисунок, верхняя часть). Для лучшего восприятия понятия порога вспомните о том, что у нас есть вероятность принадлежности к классу 1 для каждого примера. Однако вероятность еще не является меткой класса. Поэтому следует сравнивать ее с порогом для определения того, к какому классу принадлежит пример. Например, если значение порога равно 1, то все примеры должны классифицироваться как принадлежащие к классу 0, поскольку значение вероятности не может быть более 1, а значения показателей FPR и TPR при этом будут равны 0 (так как ни один из образцов не классифицируется как положительный). Такой ситуации соответствует самая левая точка на ROC-кривой. С другой стороны кривой находится точка, в которой значение порога равно 0: это означает, что все образцы классифицируются как принадлежащие к классу 1, а значения обоих показателей TPR и FPR равны 1. Промежуточные точки отображают поведение зависимости TPR/FPR при изменении значения порога.
Диагональная линия на графике соответствует случайному классификатору. Чем лучше работает наш классификатор, тем ближе его кривая к левой верхней точке графика. Таким образом, объективным показателем качества классификатора является площадь под ROC-кривой (показатель ROC AUC). Значение данного показателя должно быть как можно ближе к 1. Значение AUC, равное 0,5, соответствует случайному классификатору.
Показатель AUC в нашей модели (см. рисунок выше) равен 0,57, что является далеко не лучшим результатом.
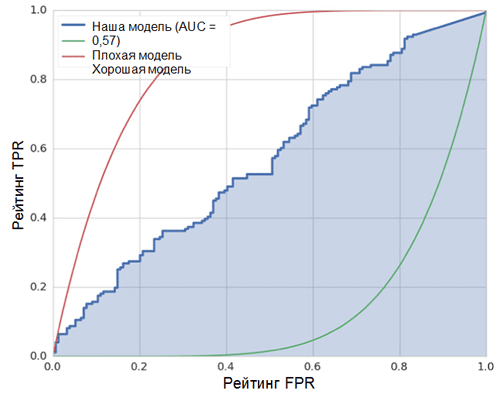
Все эти метрики свидетельствуют о том, что полученная модель лишь немногим лучше случайного классификатора. Тому есть несколько причин, далее описаны основные из них:
- Очень малый объем данных для обучения, недостаточный для выделения характерных признаков изображений. Даже аугментация данных не смогла помочь в данном случае.
- Относительно сложная модель сверточной нейросети (по сравнению с другими моделями машинного обучения) с большим количеством параметров.
Заключение
В данной статье мы создали простую модель сверточной нейронной сети для распознавания эмоций на изображениях. При этом на этапе обучения был использован ряд способов для аугментации данных, также была проведена оценка модели с использованием набора таких метрик, как: точность, ROC-кривая, показатель ROC AUC и матрица неточностей. Модель продемонстрировала результаты, лишь немногим лучшие случайных. Причиной этого является недостаточный объем доступных данных.
