[Из песочницы] Задача о переправе
На Тостере иногда встречаются вопросы о том, как научиться думать как программист. Год назад я ради развлечения решил написать программу которая решает всем хорошо известную задачку — головоломку о волке, козе и капусте. В англоязычных источниках известную как river crossing puzzle.
В этом посте я представлю вам пример мыслительного процесса от задачи к ee алгоритмическому решению.
Должен признаться, что из-за многолетнего влияния объектно-ориентированной парадигмы на мой мозг, первое, что мне пришло в голову, это для всех сущностей, участников задачи, написать классы. Проблемно-ориентированное программирование и все такое. Но я вовремя остановился, вспомнив старые учебники по паскалю, где оперировали понятиями фунцкия и процедура.
Чтобы перевести задачу в плоскость понятную машине, нам нужно избавиться от тех частей контекста задачи, который не имеет значения для ее решения.
Не имеет значения все, что нельзя выразить числами. Капуста это или мяч не имеет значения, важно, что участников четверо. Река перед ними или гора — неважно, есть два места где могут находиться участники этой задачи. На лодке они переправляются или на самолете — неважно, они могут перемещаться с одной точки в другую и наоборот, при чем в перемещении всегда задействован крестьянин (или «мужик») — особенный участник.
В полной абстракции условия будут выглядеть как-то так:
- Есть набор из трех элементов и один специальный элемент.
- Есть запрещенные комбинации элементов (при отсутствии специального элемента)
- В комбинации со специальным элементом все комбинации допустимы.
- Нужно перенести все элементы с одного места в другое, так чтобы никогда не образовывались запрещенные комбинации элементов.
- При этом переносить можно лишь один элемент, либо в одну, либо в другую сторону, поочередно. Т.е. нельзя сделать два переноса в одну сторону. — спасибо Dr_Dash за то, что заострил на этом внимание.
Чтобы различать элементы и их комбинации, нам нужно дать им идентификаторы. Машина лучше всего работает с числами — обозначим их числами. Мы хотим комбинировать элементы. Комбинировать числа значит делать над ними арифметические операции.
Тогда закодируем отдельные значения так, чтобы сумма чисел однозначно указывала на комбинацию:
0 — никого
1 — P Крестьянин (Peasant)
2 — G Коза (Goat)
4 — C Капуста (Cabbage)
8 — W Волк (Wolf)
Буквы тут только для мнемоники и никакой нагрузки не несут
То, что крестьянин обозначен числом 1 — важно. Изза этого «код конфигурации берега» с крестьянином всегда будет нечетным. Так можно будет понимать на с какой стороны он находится.
Запишем возможные комбинации на обеих берегах в виде таблицы, и отметим допустимые варианты распределения участников по берегам иксом:
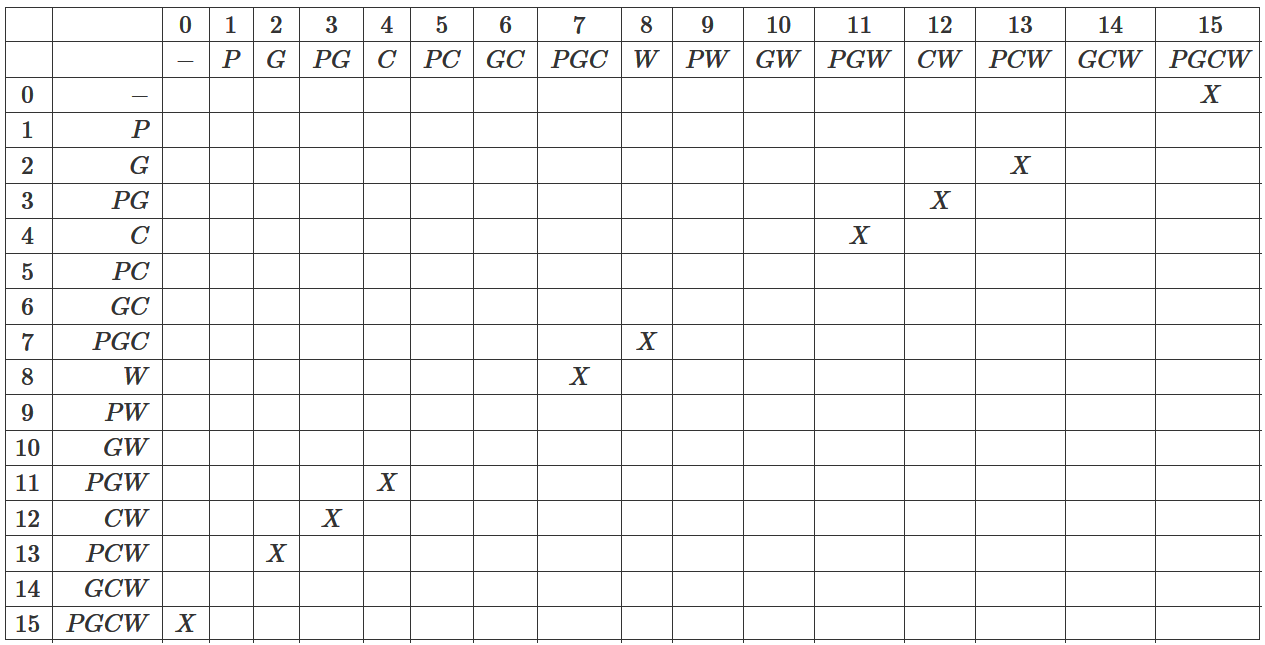
Заметим, что возможные комбинации конфигурации берегов всегда в сумме дают 15, но не все из них допустимы.
Из визуального представления в виде таблицы становится ясно, что нам нужно перейти из одного угла таблицы в другой, переходя при этом только в допустимые состояния.
Какой берег левый, а какой правый, для задачи не имеет значения. Т.е указав код конфигурации например 11, мы говорим, что на одном берегу находятся крестьянин, коза и волк. То, что капуста на другом берегу не нужно особенно указывать. Поскольку в сумме оба берега дают 15, то 4 — капуста, на другом берегу.
Представим себе, что наши состояния это камни в воде, и мы перепрыгивая с камня на камень должны переместиться с одного конца в другой. Напоминает ленту машины Тьюринга, правда?
На ленте начало обозначено черным треугольником справа, а конец — перевернутым треугольником слева. Возможные промежуточные состояния обозначены черными точками. Недопустимые состояния помечены крестиком.
Перемещаться мы можем только в допустимые состояния. Также, из условия задачи известно, что в перемещении всегда участвует крестьянин и, что лодка умещает максимум двоих. Значит, мы можем оперировать числами 1 (крестьянин), 3 (крестьянин и коза), 5 (крестьянин и капуста), 9 (крестьянин и волк).
Получается, если мы начинаем из состояния 15, когда все на одном берегу — единственное из возможных следующих состояний это 12. Из состояния 12 у нас нет другого выхода, кроме как вернуть крестьянина на другой берег, делаем +1. Переходим в состояние 13. Отсюда мы можем сделать либо -5 (перевезти капусту) либо -9 (перевезти волка). Если мы сделаем -9 то попадем в состояние 4, но крестьянина после этого надо вернуть. Одного его мы вернуть не можем, иначе мы окажемся в состоянии 5, но мы можем вернуть его с козой т.е. +3, и окажемся в состоянии 7(коза капуста и крестьянин). Отсюда мы можем сделать либо -3 (эвакуировать козу) либо -5 (спасти капусту). Поскольку -3 было бы откатом предыдущего действия, остается -5. Мы переходим в состояние 2. Отсюда мы можем сделать только +1, и +9 (поскольку +5 было бы откатом предыдущего действия, a +3 недопустимое состояние).
Заметьте, +3 невозможно здесь не потому, что «коза ведь на другом берегу» (это обьяснение понятное человеку), а потому, что это переход в недопустимое состояние («обьяснение» понятное машине). Делаем +1. Переходим в состояние 3. Делаем -3. Готово.
Но это не единственно возможное решение. Заметьте, что человеку трудно отслеживать все перемещения. Для машины же, существует набор допустимых и недопустимых состояний, и набор правил.
Давайте заставим машину найти все возможные решения задачи. T.e. найти все возможные цепочки состояний которые ведут к решению. Воспользуемся рекурсией и питоном в качестве языка.
Для хранения цепочек переходов возьмем массив. Первое состояние в массиве 15. Передадим его в фунцкию рекурсии. Определим условие окончания рекурсии. Это когда конечный элемент цепочки будет 0.
def f(states):
s = states[-1] #состояние рассматриваемое в итерации, последнее в цепочке.
if s==0: # условие остановки
print(str(states))
print("END")
else: # если условие остановки не достигнуто
...
print(f([15]))
Если состояние четное (крестьянин на другом берегу), то мы выполняем одну из возможных операций с положительным знаком (+1, +3, +5 или +9).
Для каждой возможной операции должны выполняться условия:
— она не ведет в недопустимое состояние,
— она не ведет за максимальную положительную границу ленты
— она не ведет в состояние в котором мы уже были.
Если такая операция имеется, выполни ее, и добавь новое состояние к цепочке состояний.
Передай новую цепочку состояний в рекурсивную фунцкию.
if s%2 == 0:
for i in [9,5,3,1]:
if (s+i not in [1,5,6,9,10,14]) and (s+i<=15) and (s+i not in states):
f(states+[s+i])
Если же состояние нечетное, то мы следуем тем же соображениям, но со знаком минус.
else:
for i in [9,5,3,1]:
if (s-i not in [1,5,6,9,10,14]) and (s-i>=0) and (s-i not in states):
f(states+[s-i])
def f(states):
s = states[-1]
if s==0:
print(str(states))
print("END")
else:
if s%2 == 0:
for i in [9,5,3,1]:
if (s+i not in [1,5,6,9,10,14]) and (s+i<=15) and (s+i not in states):
f(states+[s+i])
else:
for i in [9,5,3,1]:
if (s-i not in [1,5,6,9,10,14]) and (s-i>=0) and (s-i not in states):
f(states+[s-i])
print(f([15]))
На выходе получим
[15, 12, 13, 4, 7, 2, 3, 0]
END
[15, 12, 13, 8, 11, 2, 3, 0]
END
None
Заметим, что в решении четные и нечетные числа чередуются. Это перемещения крестьянина с одного берега на другой. Не зря выше мы обозначили его единицей.
Также обратим внимание на то, что изначальные условия задачи, понятные человеку, в программном решении превратились в цифры и операции над ними.
Надеюсь, кому-то эта статья окажется полезной.
P.S.:
Если у кого-то есть обьектно-ориентированное решение, то пожалуйста поделитесь им в комментариях, чтобы можно было сравнить парадигмы.
