[Из песочницы] Зачем нужны ranges из C++20 в простой числодробилке?
В последнее время интервалы (ranges), которые должны войти в стандарт C++20, довольно много обсуждают, в том числе и на Хабре (пример, где много примеров). Критики интервалов хватает, поговаривают, что
- они слишком абстрактны и нужны только для очень абстрактного кода
- читаемость кода с ними только ухудшается
- интервалы замедляют код
Давайте посмотрим совершенно рабоче-крестьянскую практическую задачку, для того, чтобы понять, справедлива ли эта критика и правда ли, что Эрик Ниблер был укушен Бартошем Милевски и пишет range-v3 только при полной луне.
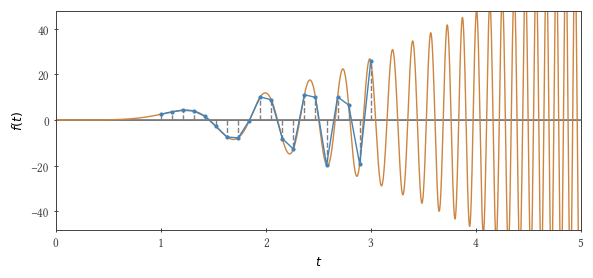
Будем интегрировать методом трапеций вот такую функцию: $inline$f (t) = 3 t^2 \sin t^3$inline$, в пределах от нуля до $inline$\tau$inline$. Если $inline$\tau^3 / \pi$inline$ равняется нечётному числу, то интеграл равен 2.
Итак, задачка: напишем прототип функции, которая вычисляет интеграл методом трапеций. Кажется, на первый взгляд, что здесь не нужны абстракции, а вот скорость важна. На самом деле, это не совсем так. По работе мне часто приходится писать «числодробилки», основной пользователь которых — я сам. Так что поддерживать и разбираться с их багами приходится тоже мне (к сожалению моих коллег — не всегда только мне). А еще бывает, что какой-то код не используется, скажем, год, а потом… В общем, документацию и тесты тоже нужно писать.
Какие аргументы должны быть у функции-интегратора? Интегрируемая функция и сетка (набор точек $inline$t_1, t_2, t_3…$inline$, используемых для вычисления интеграла). И если с интегрируемой функцией всё понятно (std::function здесь будет в самый раз), то в каком виде передавать сетку? Давайте посмотрим.
Варианты
Для начала — чтобы было, с чем сравнивать производительность — напишем простой цикл for с постоянным шагом по времени:
// trapezoidal rule of integration with fixed time step;
// dt_fixed is the timestep; n_fixed is the number of steps
double integrate() {
double acc = 0;
for(long long i = 1; i < n_fixed - 1; ++i) {
double t = dt_fixed * static_cast(i);
acc += dt_fixed * f(t);
}
acc += 0.5 * dt_fixed * f(0);
acc += 0.5 * dt_fixed * f(tau);
return acc;
} При использовании такого цикла можно передавать в качестве аргументов функции начало и конец интервала интегрирования, а еще число точек для этого самого интегрирования. Стоп — метод трапеций бывает и с переменным шагом, и наша интегрируемая функция просто просит использовать переменный шаг! Так и быть, пусть у нас будет ещё один параметр ($inline$b$inline$) для управления «нелинейностью» и пусть наши шаги будут, например, такими: $inline$\Delta t (t) = \Delta t_0 + b t$inline$. Такой подход (ввести один дополнительный числовой параметр) используется, наверное, в миллионе мест, хотя, казалось бы, ущербность его должна быть всем очевидна. А если у нас другая функция? А если нам нужен мелкий шаг где-то посередине нашего числового интервала? А если у интегрируемой функции вообще пара особенностей есть? В общем, мы должны уметь передать любую сетку. (Тем не менее в примерах мы почти до самого конца «забудем» про настоящий метод трапеций и для простоты будем рассматривать его версию с постоянным шагом, держа при этом в голове то, что сетка может быть произвольной).
Раз сетка может быть любой — передадим её значения $inline$t_1, t_2, …$inline$ завёрнутыми в std::vector.
// trapezoidal rule of integration with fixed time step
double integrate(vector t_nodes) {
double acc = 0;
for(auto t: t_nodes) {
acc += dt_fixed * f(t);
}
acc -= 0.5 * dt_fixed * f(0);
acc -= 0.5 * dt_fixed * f(tau);
return acc;
} Общности в таком подходе — хоть отбавляй, а что с производительностью? С потреблением памяти? Если раньше у нас всё суммировалось на процессоре, то теперь приходится сначала заполнить участок памяти, а потом читать из него. А общение с памятью — довольно медленная вещь. Да и память всё таки не резиновая (а силиконовая).
Посмотрим в корень проблемы. Что человеку нужно для счастья? Точнее, что нужно нашему циклу (range-based for loop)? Любой контейнер с итераторами begin() и end(), и операторами ++, * и != для итераторов. Так и напишем.
// функция стала шаблоном, чтобы справиться со всем, что в неё задумают передать
template
double integrate(T t_nodes) {
double acc = 0;
for(auto t: t_nodes) {
acc += dt_fixed * f(t);
}
acc -= 0.5 * dt_fixed * f(0);
acc -= 0.5 * dt_fixed * f(tau);
return acc;
}
// ...
// Вот здесь всё самое интересное
class lazy_container {
public:
long long int n_nodes;
lazy_container() {
n_nodes = n_fixed;
}
~lazy_container() {}
class iterator {
public:
long long int i; // index of the current node
iterator() {
i = 0;
}
~iterator() {}
iterator& operator++() { i+= 1; return *this; } // вот!
bool operator!=(const iterator& rhs) const { return i != rhs.i; }
double operator* () const
{ return dt_fixed * static_cast(i); }
};
iterator begin() {
return iterator();
}
iterator end() {
iterator it;
it.i = n_nodes;
return it;
}
};
// ...
// а так это можно использовать
lazy_container t_nodes;
double res = integrate(t_nodes); Мы вычисляем здесь новое значение $inline$t_i$inline$ по требованию, так же, как мы делали это в простом цикле for. Обращений к памяти при этом нет, и можно надеяться, что современные компиляторы упростят код очень эффективно. При этом код интегрирующей функции почти не поменялся, и она по-прежнему может переварить и std::vector.
А где гибкость? На самом деле мы теперь можем написать любую функцию в операторе ++. То есть такой подход позволяет, по сути, вместо одного числового параметра передать функцию. Генерируемая «на лету» сетка может быть любой, и мы к тому же (наверное) не теряем в производительности. Однако писать каждый раз новый lazy_container только ради того, чтобы как-то по-новому исказить сетку совсем не хочется (это же целых 27 строк!). Конечно, можно функцию, отвечающую за генерацию сетки, сделать параметром нашей интегрирующей функции, и lazy_container тоже куда-нибудь засунуть, то есть, простите, инкапсулировать.
Вы спросите — тогда что-то опять будет не так? Да! Во-первых, нужно будет отдельно передавать число точек для интегрирования, что может спровоцировать ошибку. Во-вторых, созданный неstанdартный велосипед придётся кому-то поддерживать и, возможно, развивать. Например, сможете сходу представить, как при таком подходе сочинить комбинатор для функций, стоящих в операторе ++?
C++ более 30 лет. Многие в таком возрасте уже заводят детей, а у C++ нет даже стандартных ленивых контейнеров/итераторов. Кошмар! Но всё (в смысле итераторов, а не детей) изменится уже в следующем году — в стандарт (возможно, частично) войдёт библиотека range-v3, которую уже несколько лет разрабатывает Эрик Ниблер. Воспользуемся трудами его плодов. Код скажет всё сам за себя:
#include
#include
//...
auto t_nodes = ranges::v3::iota_view(0, n_fixed)
| ranges::v3::views::transform(
[](long long i){ return dt_fixed * static_cast(i); }
);
double res = integrate(t_nodes); Интегрирующая функция осталась прежней. То есть всего 3 строчки на решение нашей проблемы! Здесь iota_view(0, n) генерирует ленивый интервал (range, объект, который инкапсулирует обобщённые begin и end; ленивый range — это view), который при итерировании на каждом шаге вычисляет следующее число в диапазоне [0, n). Забавно, что название ι (греческая буква йота) отсылает на целых 50 лет назад, к языку APL. Палка | позволяет писать цепочки (pipelines) модификаторов интервала, а transform, собственно, и является таким модификатором, который с помощью простой лямбда-функции превращает последовательность целых чисел в ряд $inline$t_1, t_2,…$inline$. Всё просто, как в сказке Haskell.
А как всё-таки сделать переменный шаг? Всё так же просто:
В качестве фиксированного шага мы брали десятую часть периода нашей функции вблизи верхнего предела интегрирования $inline$\Delta t_{fixed} = 0.1 \times 2 \pi / 3 \tau^2$inline$. Теперь шаг будет переменный: можно заметить, что если взять $inline$t_i = \tau (i / n)^{⅓}$inline$, (где $inline$n$inline$ — общее число точек), то шаг будет $inline$\Delta t (t) \approx dt_i/di = \tau^3 / (3 n t^2)$inline$, что составляет десятую часть периода интегрируемой функции при данном $inline$t$inline$, если $inline$n = \tau^3 / (0.1 \times 2 \pi)$inline$. Остаётся «подшить» это к какому-нибудь разумному разбиению при малых значениях $inline$i$inline$.
#include
#include
#include
//...
// trapezoidal rule of integration; step size is not fixed
template
double integrate(T t_nodes) {
double acc = 0;
double t_prev = *(t_nodes.begin());
double f_prev = f(t_prev);
for (auto t: t_nodes | ranges::v3::views::drop(1)) {
double f_curr = f(t);
acc += 0.5 * (t - t_prev) * (f_curr + f_prev);
t_prev = t;
f_prev = f_curr;
}
return acc;
}
//...
auto step_f = [](long long i) {
if (static_cast(i) <= 1 / a) {
return pow(2 * M_PI, 1/3.0) * a * static_cast(i);
} else {
return tau * pow(static_cast(i) / static_cast(n), 1/3.0);
}
};
auto t_nodes = ranges::v3::iota_view(0, n)
| ranges::v3::views::transform(step_f);
double res = integrate(t_nodes); Внимательный читатель заметил, что в нашем примере переменный шаг позволил уменьшить число точек сетки в три раза, при этом дополнительно возникают заметные расходы на вычисление $inline$t_i$inline$. Но если мы возьмём другую $inline$f (t)$inline$, число точек может измениться гораздо сильнее… (но здесь автору уже становится лень).
Итак, тайминги
У нас есть такие варианты:
- v1 — простой цикл
- v2 — $inline$t_i$inline$ лежат в
std::vector - v3 — самодельный
lazy_containerс самодельным итератором - v4 — интервалы из C++20 (ranges)
- v5 — снова ranges, но только здесь метод трапеций написан с использованием переменного шага
Вот что получается (в секундах) для $inline$\tau = (10\,000\,001 \times \pi)^{⅓}$inline$, для g++ 8.3.0 и clang++ 8.0.0 на Intel® Xeon® CPU® X5550 (число шагов около $inline$1.5 \times 10^8$inline$, кроме v5, где шагов в три раза меньше (результат вычислений всеми методами отличается от двойки не более, чем на 0.07):
g++ -O3 -ffast-math -std=c++2a -Wall -Wpedantic -I range-v3/include
clang++ -Ofast -std=c++2a -Wall -Wpedantic -I range-v3/include
В общем, муха по полю пошла, муха денежку нашла!
Кому-то это может быть важно
Итог
Даже в очень простой задаче интервалы (ranges) оказались очень полезными: вместо кода с самодельными итераторами на 20+ строк мы написали 3 строки, при этом не имея проблем ни с читаемостью кода, ни с его производительностью.
Конечно, если бы нам была нужна (за)предельная производительность в этих тестах, мы должны были бы выжать максимум из процессора и из памяти, написав параллельный код (или написать версию под OpenCL)… Также я понятия не имею, что будет, если писать очень длинные цепочки модификаторов. Легко ли отлаживать и читать сообщения компилятора при использовании ranges в сложных проектах. Увеличится ли время компиляции. Надеюсь, кто-нибудь когда-нибудь напишет и про это статью.
Когда я писал эти тесты, я сам не знал, что получится. Теперь знаю — ranges однозначно заслужили того, чтобы их протестировать в реальном проекте, в тех условиях, в которых вы предполагаете их использовать.
Ушёл на базар покупать самовар.
Полезные ссылки
range-v3 home
Документация и примеры использования v3
код из этой статьи на github
списки в haskell, для сравнения
Благодарности
Спасибо fadey, что помог с написанием этого всего!
P.S.
Надеюсь, кто-нибудь прокомментирует вот такие странности: i) Если взять в 10 раз меньший интервал интегрирования, то на моём Xeon пример v2 оказывается на 10% быстрее, чем v1, а v4 в три раза быстрее, чем v1. ii) Интеловский компилятор (icc 2019) иногда в этих примерах делает код, который оказывается в два раза быстрее, чем скомпилированный g++. Векторизация виновата? Можно g++ заставить делать так же?
