[Из песочницы] Взлом шифра Виженера с помощью частотного криптоанализа
«Представьте себе такую ситуацию… Как-то раз, уходя со службы около часу ночи (руководитель должен подавать хороший пример), вы замечаете торчащий в дверях измятый клочок бумаги… Бумага отменная, слегка пахнет мускусом; почерк явно женский и веет от него этаким французским шармом. Теперь, по здравом размышлении, новая сотрудница мисс Хари начинает казаться вам, пожалуй, немножко слишком экзотичной. Ее французский акцент, неизменное черное платье для коктейля, нитка черного жемчуга, подчеркивающая декольте, и этот будоражащий запах мускуса, наполняющий комнату, когда она входит… Она говорит, что работала раньше в региональном вычислительном центре Мак-Дональда в Киокаке. Что-то тут не так. Подождите… Неужели мисс Хари шпионит в пользу знаменитой французской фирмы И Бей Эм? А эта записка — шифровка, в которой все секреты вашего новейшего чудо-компилятора? Чтобы уличить мисс Хари, записку нужно расшифровать. Но как?»
На Хабре уже пару раз мелькали статьи о книге Чарльза Уэзерелла «Этюды для программистов». Перед вами фрагмент одного из самых интересных, на мой взгляд, этюдов — «Секреты фирмы», основной задачей в котором является взлом шифра Виженера. Не так давно я реализовал этот этюд, и в моей статье я расскажу о том, как я это сделал и что в итоге получилось.
Задача
Автор предлагает нам написать программу, которая позволит взломать шифр Виженера, а точнее, одну из его модификаций. Текст шифруется следующим образом. Составляется таблица, т. н. квадрат Виженера: сверху и по левому краю записывается алфавит, затем в первую строку помещается некоторая перестановка исходного алфавита, во вторую — эта же перестановка, циклически сдвинутая на одну позицию, и так далее. В результате мы получаем таблицу, которая сопоставляет каждой паре символов какой-то символ.
Затем выбирается ключевое слово и многократно записывается под исходным текстом. Наконец, каждая пара (символ исходного текста; символ ключевого слова под ним) шифруется с помощью таблицы соответствующим этой паре символом. Например, фраза «звезда забега» будет зашифрована с помощью ключа «багаж» и приведенной выше таблицы так:
Идея решения
Рассмотрим обратный квадрат Виженера, то есть таблицу, которая сопоставляет паре (символ зашифрованного текста; символ ключевого слова) символ исходного текста.
Договоримся называть дистанцией между двумя символами разность их позиций в алфавите: например, дистанция между 'а' и 'в' — это 2. Тогда можно заметить, что если дистанция между i-м и j-м символами ключевого слова равна d, то дистанция между соответствующими символами исходного текста составляет -d. Следовательно, если нам удастся найти ключевое слово, то мы сможем свести шифр Виженера к шифру простой замены: каждая буква исходного текста будет заменена на другую, при этом соответствие букв будет взаимно-однозначным. Взломать такой шифр не составит труда.
Остается найти ключевое слово. Пусть нам известно, что длина ключевого слова — L символов. Тогда текст можно разбить на L групп, каждая из которых будет зашифрована с помощью одного символа ключевого слова, т. е. это будет шифр простой замены. При этом используемые перестановки алфавита будут отличаться лишь сдвигом, равным с точностью до знака дистанции между соответствующими символами ключевого слова. Используя методы частотного криптоанализа, мы сможем определить эти сдвиги.
Таким образом, программа будет состоять из трех частей:1) Определение длины ключевого слова2) Поиск ключевого слова3) Поиск перестановки алфавита и расшифровка текста
Длина ключевого слова
Длину ключевого слова проще всего найти, используя метод индекса совпадений. Этот метод был предложен Уильямом Фридманом в 1922 году для взлома оригинального шифра Виженера, но он сработает и в нашем случае. Метод основан на том факте, что вероятность совпадения двух случайных букв в некотором достаточно длинном тексте (индекс совпадений) — это постоянная величина. Таким образом, если разбить текст на L групп символов, каждая из которых зашифрована шифром простой замены (напомню, это и означает, что L — длина ключевого слова), то индексы совпадений для каждой из групп будут довольно близки к теоретическому значению этой величины; для всех других разбиений индексы совпадений будут гораздо ниже. Индекс совпадений можно посчитать по формуле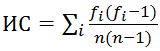
(fi — количество i-х букв алфавита в тексте, а n — его длина)
Ниже, например, приведены индексы совпадений для текста, зашифрованного с помощью ключа «проект» (6 символов).
Таким образом, для определения длины ключевого слова нужно посчитать индексы совпадений для разбиения текста на L = 1, 2, … групп, а затем выбрать из полученных величин первую, значительно превосходящую большинство остальных. Но… тут есть небольшая хитрость. Что если текст зашифрован с использованием ключа, который можно разделить на несколько похожих частей? Снизу приведена таблица индексов совпадений для того же текста, что и в первом примере, но зашифрованного с помощью ключа «космос» (те же 6 символов). Как же определить длину ключа в таком случае?
Я поиграл с различными способами и выяснил, что проще всего выбрать необходимый индекс так: нужно взять первый индекс, для которого справедливо: 1.06*ИС > ИСi, i = 1, 2, … Умножения на 1.06 в большинстве случаев хватает, чтобы настоящий ИС стал превосходить «кратные» ИС (в нашем примере это индексы при L = 12 и 18), но недостаточно для того, чтобы ложные индексы (при L = 3, 9 и 15) превзошли настоящие.
Конечно, мой способ не дает 100% результат. Более того, если текст зашифрован с помощью слова, состоящего из одинаковых частей (например, «тартар»), то длина ключевого слова в любом случае будет определена неверно (если, конечно, мы хотим найти осмысленное ключевое слово): нет никакой разницы между шифрованием ключом «тартар» и «тар». Поэтому важно дать пользователю возможность изменять длину ключа в ходе работы программы: к примеру, не подошла 6, значит, стоит попробовать 3 или 12.К счастью, для зашифрованной записки из книги все определяется довольно просто. Взглянув на таблицу индексов совпадений, можно с уверенностью сказать, что длина ключевого слова — 7 символов.
Ключевое слово Теперь, когда длина ключа найдена, можно приступить к поиску самого ключевого слова. Сперва нужно определить вероятности различных сдвигов между группами, на которые мы разбили шифр (напомню, что каждая группа зашифрована с помощью некоторой перестановки алфавита, при этом перестановки отличаются лишь сдвигом каждой буквы на несколько позиций в алфавите). Для нахождения вероятностей сдвигов я воспользовался идеей, предложенной переводчиками «Этюдов». Если опустить все математические выкладки, она заключается в следующем. Для каждой группы мы считаем количество символов x (x = 'а', 'б', …, 'я') в ней и на основании информации о частоте букв в русском языке оцениваем вероятность того, что символу x шифра соответствует символ y (y = 'а', 'б', …, 'я') исходного текста. Сопоставляя полученные таблицы вероятностей для различных групп, мы можем вычислить вероятности сдвигов r (r = 1, 2, …, 32) между этими группами. В результате мы получаем таблицу, показывающую, какова вероятность сдвига r между группами i и j для любых двух групп и любого сдвига.Найти само ключевое слово можно двумя способами. Первый способ — это найти наилучшую конфигурацию сдвигов, используя (только) полученную таблицу. Полный перебор занял бы очень много времени, поэтому я пошел другим путем. Я искал ключ следующим образом. Возьмем любое слово подходящей длины и вычислим его характеристику — сумму вероятностей сдвигов между каждыми двумя символами в нем (сдвиги между символами ключевого слова и между буквами перестановок в различных группах шифра совпадают с точностью до знака). Теперь внесем небольшое изменение в исследуемое слово. Если после изменения характеристика слова стала лучше, то мы запоминаем новое слово, в противном же случае забываем новое слово и возвращаемся к старому. Внося таким образом случайные изменения, мы довольно быстро найдем лучшее слово.
Проблема заключается лишь в том, что наилучшее слово далеко не всегда является ключевым. Тесты показали, что уже для текстов из 1024 символов ключ и лучшее слово зачастую различаются на один символ. Например, лучшее слово для записки из книги — «федиска». Не знаю я такого слова! Для более коротких текстов ключ определяется совершенно неверно. Поэтому от поиска ключа на основании только таблицы пришлось отказаться.
Второй способ поиска ключа простой и неинтересный, зато эффективный. Мы берем словарь и вычисляем характеристику каждого подходящего слова (для повышения скорости работы программы я разделил слова по их длинам). Лучшее слово мы берем в качестве ключевого. Такой метод работает корректно даже для коротких (400–500 символов) текстов, но у него есть очевидный недостаток: если ключевого слова нет в словаре, то программа ни при каких условиях не сработает верно.
Впрочем, если ключ в словаре есть, второй метод гораздо эффективнее первого. Поэтому в своей программе я использовал его. Этот метод сразу же дал правильное (как выяснилось позднее) ключевое слово — «редиска».
Перестановка алфавита
Имея ключевое слово, мы можем модифицировать текст так, что он окажется зашифрован шифром простой замены. Для этого необходимо циклически сдвинуть символы L-ой группы (L = 2, 3, …, длина ключа) на дистанцию между первой и L-ой буквами ключевого слова влево по алфавиту. После внесения этих изменений нам остается найти, какие буквы исходного текста соответствуют символам шифротекста.Попробуем сделать это тем же способом, каким мы искали ключевое слово без словаря. Возьмем любую таблицу соответствий между символами исходного и зашифрованного текстов (например, предположим, что букве 'а' соответствует буква 'а', букве 'б' — 'б', и т. д.) и расшифруем текст с её помощью. Посчитаем количество всевозможных биграмм (сочетаний по 2 буквы) в полученном тексте. Сравнив результат с эталонной таблицей, вычислим характеристику полученного текста (я вычислял характеристику так: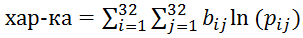 
(b_ij — количество биграмм в «расшифрованном» тексте, а p_ij — вероятность встречи определенной биграммы в русском языке)
Затем будем вносить случайные изменения в таблицу соответствий и на каждом шаге вычислять новую характеристику. Если новая характеристика оказывается лучше (больше) старой, запоминаем изменения, иначе откатываем их. В результате у нас получается правильная таблица соответствий букв, и мы можем восстановить исходный текст!
Насколько быстро работает этот алгоритм поиска перестановок? Ниже приведен график зависимости характеристики перестановок от числа итераций для зашифрованной записки из книги (для других текстов графики получаются аналогичными). На горизонтальной оси откладывается число итераций, на вертикальной — характеристика полученного текста. Изменения характеристики происходят рывками при каждом нахождении лучшей таблицы, поэтому для наглядности график представляет из себя интерполированные точки, в которых происходили изменения. Когда линия графика становится прямой и горизонтальной, правильная таблица перестановок найдена.
Также интересно взглянуть на графики зависимости номера итерации от номера успешного изменения таблицы перестановок (слева) и характеристики текста от номера изменения таблицы (справа).
Мы видим, что характеристика текста изменяется с каждым изменением таблицы перестановок более-менее линейно, а число попыток, необходимых для нахождения нового успешного изменения таблицы растет довольно быстро. Зависимость характеристики текста от числа итераций похожа на логарифмическую. Действительно, по нижним графикам видно, что если x — число итераций, y — характеристика и t — номер успешного изменения таблицы, то x∼e^t, y∼t, следовательно, y∼ln (x). Логарифм растет довольно медленно, но его рост не ограничен асимптотами, поэтому на нахождение правильной таблицы соответствий уходит довольно большое, но не бесконечное количество работы. Впрочем, тесты показывают, что 10 — 12 тысяч итераций всегда достаточно.
Заключение
После реализации описанных алгоритмов и добавления графического интерфейса получилась вот такая программа: 
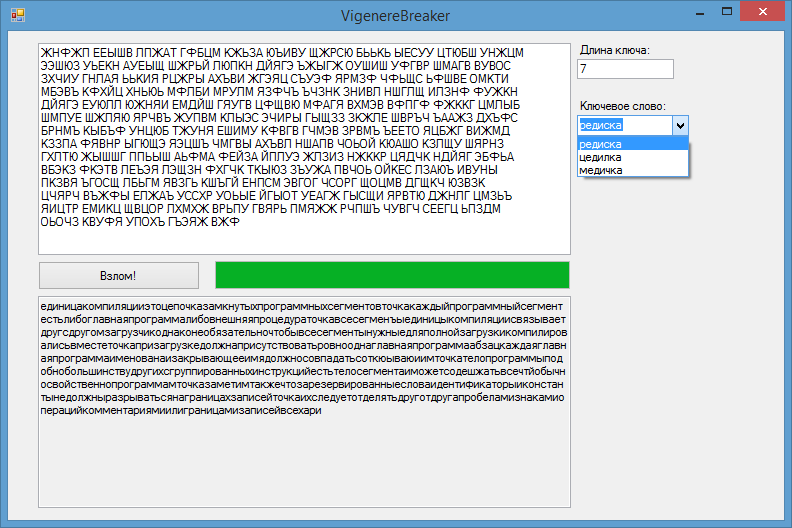
Программа успешно расшифровывает тексты длиной 400–500 символов и больше, время работы не превышает 10 секунд. Я думаю, это неплохой результат.
