[Из песочницы] В поисках лучшего бенчмарка для нейросетей
 Бывало ли у вас так — быстро запомнил что-то, а через некоторое время «прозрел», почему оно именно так? Например, можно просто запомнить, что антиградиент — это направление быстрейшего спуска. А можно представить себе геометрический смысл частной производной, провести в уме плоскости/касательные и понять, что антиградиент и правда обязан показывать направление спуска.
Бывало ли у вас так — быстро запомнил что-то, а через некоторое время «прозрел», почему оно именно так? Например, можно просто запомнить, что антиградиент — это направление быстрейшего спуска. А можно представить себе геометрический смысл частной производной, провести в уме плоскости/касательные и понять, что антиградиент и правда обязан показывать направление спуска.
Как отличить, нейросеть поняла или просто запомнила? И какой бенчмарк позволит численно это померить?
Что vs Почему
Для теста «в лоб» оба случая выглядят, понятное дело, одинаково:
- мы говорим сети, что антиградиент показывает направление спуска
- мы спрашиваем ее, что такое антиградиент
- она отвечает, что это направление спуска
То есть, вопрос «что» не очень подходит. Он проверяет больше память, чем понимание. Для проверки понимания люди обычно задают друг другу вопрос «почему». В ответ ожидается доказательство целевого утверждения (про быстрейший спуск), исходя из базовых понятий (плоскость, вектор и т.д.). Такой ответ покажет, что у отвечающего образ «антиградиент» связан причинно-следственными связями с другими вещами.
Есть другой вариант ответа — «я часто видел, что антиградиент показывал направление спуска, и потому он, может быть, всегда так делает». Такой ответ значит, что сеть нашла корреляцию и сделала по ней обобщающую гипотезу. Но — не построила причинно следственные связи к этому понятию. То есть она не поняла его.
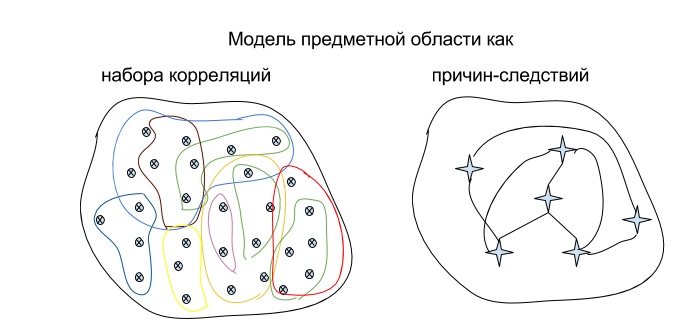
В обоих случаях она могла бы успешно применять термин — понимая его или нет.
Что меряют бенчмарки сегодня
Бенчмарки по распознаванию картинок или видео похожи на вопрос «что» (что там на картинке?). Для их успешного прохождения, видимо, достаточно лишь хорошо вытаскивать корреляции (наличие уха плюс наличие усов на картинке коррелирует с меткой «кот»).
Если посмотреть на результаты бенчмарков, в которых сети нужно генерировать осмысленные фразы, то они тоже, пожалуй, могли бы быть достигнуты с использованием только знаний о корреляциях (слово «снег» часто стояло рядом со словом «выпал», поэтому будем ставить их рядом, что бы это ни значило).
Или вот возьмем игру в го. Просмотрев 100500 законченных партий можно подметить корреляции вида: такой-то ход черным камешком в контексте таких-то фич на доске коррелировал с увеличением вероятности выигрыша черных (в просмотренных партиях). Запомнив очень много таких корреляций, можно систематически делать удачные ходы.
Но даже 100%ная корреляция между двумя переменными не значит причинно-следственности. И среди сегодняшних бенчмарков мне пока не попадалось таких, которые это бы учитывали и проверяли у сетки что-то большее, чем умение вытягивать корреляции. Значит, надо придумать такой.
Потыкаем проблему палочкой
Корреляция между двумя переменными значит, что между ними есть связь. Причинно-следственная связь — лишь частный случай понятия связь.
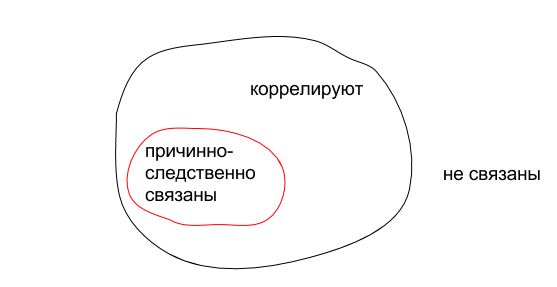
Но этот случай очень важен, потому что ПС-связи помогают строить более качественные ответы на вопрос «почему». И делать более качественные прогнозы (чем если бы мы основывались на всех подряд корреляциях).
Пример:
Количество потребляемого мороженного коррелирует с количеством солнечных ударов. Если предположить, что корреляция всегда верна, то логично ждать, что если мы станем меньше есть мороженого, то и ударов станет меньше. Но на самом деле обе величины (и мороженое, и удары) независимо следуют из жары на улице. Зная это, нам уже не придет в голову бороться с ударами, уменьшая мороженное.
Знать причинно-следственные связи == понимать?
Сложность в том, что причинно-следственные связи бывают разного качества. Возьмем для иллюстрации простенькую предметную область, где все крутится вокруг хищников и жертв:
Есть две популяции - хищники и жертвы. Чем больше жертв и чем чаще они попадаются хищникам - тем сытнее живется хищникам, и хищники лучше плодятся. Чем больше расплодилось хищников, тем сильнее страдает популяция жертв. А за жертвами и хищники тоже вымирают - потому что им нечего есть.
Такое описание предметной области — это, по сути, некий набор причинно-следственных связей, которые «прокинуты» между ее сущностями.
Эту же предметную область можно описать иначе, парой формул:
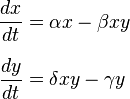
Второе описание тоже задает причинно-следственные связи между сущностями. Оба описания каждое позволяет объяснять события (то есть отвечать на вопросы типа «Почему хищников стало много?»). Значит, о какой-то степени понимании речь идет и там, и там.
Но только второе описание позволяет предсказать состояние «мира» с любой точностью и для любого интервала времени:
Вторая модель выдает наилучшее возможное качество реверсинжиниринга. Выглядит логично связать степень понимания предметной области с качеством реверсинжиниринга ее законов. Осталось продумать, каковы критерии этого качества и как их мерить.
Общий подход к измерению
Нейросеть внутри себя строит модель предметной области. Сначала эта модель — бессмысленный шум. Потом она начинает уточняться. И в идеале — сеть должна бы построить такую модель, которая была бы эквивалентна полному реверсинжинирингу предметной области.

Внутрь нейросети мы заглянуть толком не можем, ведь память сети это просто каша из миллионов чисел. Поэтому нужно заставить саму сеть «выписать» сформировавшуюся у неё модель предметной области на обозрение «внешнего аудитора», который затем оценит эту модель мерками теории информации.
Уточняем детали
Первые грабли тут — это язык, на котором наша сеть будет выдавать построенную ею модель. Например, одну и ту же вещь на естественном языке можно сказать тучей способов, что затруднит автоматическую оценку построенной сетью модели. Ну, и еще сетке пришлось бы освоить естественный язык, что само по себе звучит больно. Так что все естественные языки отметаем.
Но зато подошел бы какой-нибудь несложный язык программирования. Такой, где не надо думать о приведении типов и управлении памятью, а можно просто описывать алгоритмы. Назовем его язык Х.
Тогда тест на понимание предметной области выглядит так:
- Генерируем предметную область как функцию, написанную на языке Х
outputParams sandbox(inputParams, t);Для нее создаем набор тестов, проверяющих простые и «граничные» случаи. Мы это можем сделать, потому что знаем ее внутреннюю структуру. - Даем нашей нейросети поисследовать эту функцию методом черного ящика. Нейросеть может задавать любые, какие захочет, inputParams, и смотреть, что вернула функция в outputParams.
- Когда сеть решает, что она «поняла», то она генерирует нам текстовый файлик с кодом на языке Х.
- Мы автоматически запускаем сгенерированный сетью код, и прогоняем на нем наши тесты, ранее написанные для sandbox. Если тесты успешно прошли, значит, сетке удалось составить эквивалентную sandbox программу. Теперь наступает самый важный момент в бенчмарке — надо сравнить информационную сложность нашей и её программ. И сам собой здесь напрашивается подход Колмогорова.
Колмогоровская сложность предметной области и ее модели
Пусть предметная область — она же функция sandbox — всегда выдает «abababababababababab». Нейросеть могла бы предположить, что внутри sandbox это задано так:
{
print a;
print b;
print a;
print b;
… //всего 20 строк, т.к. там 20 букв
}
А другая сеть могла бы предположить:
{
for(1...10)
{
print a;
print b;
}
}
Программистам интуитивно понятно, что вторая программа «лучше». Потому что во втором случае в коде программы отражен закон, а в первом — «захардкожены» его проявления.
Будем считать длину программы таким образом: каждое вхождение имени переменной дает +1 к длине. И то же самое для всех операторов (for, if, print, +,*, {, и т.д.). Тогда для языка Х и данной предметной области найдется такая длина программы, меньше которой описание этой предметной области быть не может. Назовем эту длину эталоном. Чем ближе длина кода, полученного от нейросети, к эталону, тем лучше её код соответствует реальной алгоритмической сложности этой предметной области.
В качестве эталонна можно, за неимением лучшего, рассмотреть длину кода sandbox, т.к. он был написан человеком.
Если нейросеть добилась длины кода, равной эталону для предметной области, то за реверсинжиниринг этой области она получает заслуженный 1 балл (при условии, что тесты на ее коде успешно прошли, конечно). Один балл значит 100%. Ведь в самом деле, если две программы ведут себя одинаково, и информационная сложность у них одинаковая, то что еще надо для признания реверсинжиниринга успешным?
Если длина программы получилась супер-большая, то оценка за реверсинжиниринг стремится к нулю. Потому что сетка, скорей всего, захардкодила проявления законов, а не законы. Если полученная программа фейлит тесты, то оценка ноль — реверсинжиниринг вообще не удался.
Если реверсинжиниринг текущей предметной области прошел более-менее успешно, то имеет смысл скормить этой сетке следующую, более сложную sandbox. И делать так до тех пор, пока для очередного sandbox-a она не зафейлит тесты. Итоговый результат бенчмарка можно считать, например, как площадь под графиком:
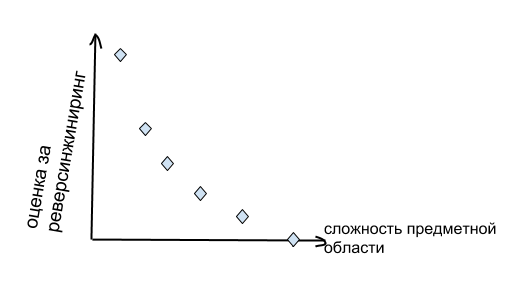
Какой профит от всего этого
Если мы серьезно подойдем к бенчмарку про, например, распознавание картинок, и будем добиваться, чтоб наши сети проходили его все лучше и лучше, то очередная сеть в этом ряду станет прекрасным распознавателем картинок. Но сможет ли эта сеть помочь нам придумать лекарство от рака? Или доказать P=NP? Ответ не очевиден. Лично мне хотелось бы от нейросетей чего-то такого: мы ей скармливаем микробиологию, она ее сама изучает и выдает нам ответ, как вылечить рак/альцгеймер/etc.
Для этого неплохо иметь такой бенчмарк, который численно мерил бы способность сетки самостоятельно реверсинжинирить законы, управляющие предметными областями. Тогда, если начать с простых искусственных предметных областей, и добиваться того, чтоб сети могли реверсинжинирить все более и более сложные области, то очередная сеть в этом ряду сможет успешно работать и с реверсинжинирингом реального мира. И поможет нам уже с раком, наконец.
