[Из песочницы] Типичные ошибки начинающих работать с изображениями
 Цифровая обработка изображений — весьма интересная область, но она таит в себе множество подводных камней, на которые постоянно натыкаются новички. Мы активно привлекаем студентов к участию в грантах и проектах, но когда мы пытались давать студентам реальные задания, которые требуют реализации новых алгоритмов обработки изображений, мы были в ужасе от совершаемых ими детских ошибок.
Цифровая обработка изображений — весьма интересная область, но она таит в себе множество подводных камней, на которые постоянно натыкаются новички. Мы активно привлекаем студентов к участию в грантах и проектах, но когда мы пытались давать студентам реальные задания, которые требуют реализации новых алгоритмов обработки изображений, мы были в ужасе от совершаемых ими детских ошибок.
Поэтому перед постановкой полноценных задач мы стали давать студентам ряд практических заданий по реализации стандартных алгоритмов обработки изображений: базовые операции над изображениями (поворот, размытие), свёртка, интерполяция с помощью простых фильтров (билинейная, бикубическая), направленная интерполяция, выделение границ с помощью алгоритма Канни, детектирование ключевых точек и т.д. Язык программирования мог быть любым, однако при выполнении заданий не допускается использование сторонних библиотек, за исключением чтения и записи изображений. Это связано с тем, что задания носят обучающий характер, самостоятельная реализация алгоритмов является хорошей практикой в программировании и позволяет понять, как работают методы изнутри.
Данная статья описывает наиболее частые ошибки, совершаемые студентами при выполнении практических заданий по обработке изображений. Изображения обычные, никакой экзотики типа 16-битной глубины цвета, панхроматичности и 3D-изображений нет.
Ошибка 1. Работа с пикселями, используя системные объекты Bitmap, HBITMAP и им подобные для хранения изображений
Данные объекты предназначены для взаимодействия с графической подсистемой (рисование примитивов и текста, вывод на экран) и не предоставляют возможности прямого доступа к участку памяти, в котором хранятся пиксели изображения. Доступ к пикселям осуществляется с помощью функций GetPixel и SetPixel. Вызов этих функций очень дорогой — на два-три порядка медленнее, чем прямой доступ к пикселям. Особенно велик соблазн так делать в C#, где тип Bitmap доступен «из коробки».
Решение: использовать данные классы только для чтения из файла, записи в файл и вывод на экран, в остальных случаях работать с классами, имеющими эффективный доступ к пикселям.
Замечание: в некоторых случаях в Windows удобно работать с DIB (device independent bitmap): есть и прямой доступ к пикселям, и возможность вывода на экран, минус — ограничение на тип пикселя.
Ошибка 2. Использование библиотек для работы с изображениями при отсутствии опыта обработки изображений
Использование библиотек чревато непониманием работы алгоритмов и дальнейшими трудностями при решении практических задач, требующих разработки собственных алгоритмов, которых нет в библиотеках. Я сталкивался с хорошо программирующими студентами, которые не могли реализовать даже элементарные операции типа свёртки: то не получалось подключить библиотеку, то работало не так, но на написание функции из 10 строчек ума уже не хватало.
Решение: не использовать сторонние библиотеки, а писать свои классы для работы с изображениями и самостоятельно реализовывать основные алгоритмы. Особенно полезно это для тех, кто не имеет достаточного опыта программирования. Лучше несколько раз сломать велосипед, чем завалить целый проект из-за глупых ошибок.
Ошибка 3. Потеря в точности при округлении
В результате применения различных алгоритмов обработки изображений возникают промежуточные результаты, имеющие вещественный тип. Пример: практически любой усредняющий фильтр, например, фильтр Гаусса. Приведение результатов к типу byte приводит к внесению дополнительной ошибки и менее точной работе алгоритмов.
Ниже приведён пример работы алгоритма детектировании контуров Канни, одним из составных частей которого является вычисление модуля градиента. Слева — модуль градиента после вычисления хранится в типе float, справа — округляется до byte.


Несложно заметить, что при округлении контуры становятся рваными.
Решение: используйте тип float вместо byte для хранения значений пикселей, не занимайтесь преждевременной оптимизацией — сначала добейтесь нормальной работы алгоритма на float, а затем уже думайте, где можно использовать byte так, чтобы не снизилось качество.
Замечание: скорость работы современных процессоров с вещественными числами такая же быстрая, как и с целыми. Часто бывает даже, что операции с float выполняются быстрее, чем с byte.
Использование типа byte обычно оправдано только при использовании векторных операций, когда скорость доступа к памяти становится узким местом.
Ошибка 4. Выход значений пикселей за пределы диапазона [0, 255]
У вас нет проблем с точностью и вы всё ещё хотите для хранения значений пикселей использовать тип byte? Тогда возникает ещё одна проблема: многие операции, например бикубическая интерполяция или повышение резкости, приводят к появлению значений, выходящих за пределы указанного диапазона. Если не учитывать этот факт, то возникает эффект, называемый wrapping: значение 260 превращается в 4, а –3 — в 253. Появляются яркие точки и линии на тёмном фоне и тёмные — на светлом (слева — правильная реализация, справа — с ошибкой).


Решение: при выполнении промежуточных операций проверяйте на каждом шаге диапазон возможных значений, а при преобразовании в байтовый тип обязательна проверка на выход за границы диапазона, например, так:
unsigned char clamp(float x)
{
return x < 0.0f ? 0 : (x > 255.0f ? 255 : (unsigned char)x);
}Ошибка 5. Потеря значений в результате приведения к диапазону [0, 255]
Вы упираетесь и по-прежнему отказываетесь от использования типа float и вызываете функцию clamp? А вы уверены, что ничего не теряете, как в случае с округлением?
Видел на практике, как студенты при вычислении производной или при применении фильтра Собеля таким образом теряли отрицательные значения.
Решение: используйте float для хранения промежуточных результатов, а функцию clamp только для сохранения в файл или вывода на экран. Для визуализации производной добавляйте 128 к значению пикселя, либо берите модуль.
Ошибка 6. Неправильный порядок обхода по пикселям изображения, приводящий к замедлению работы программы
Память в компьютере одномерна. Двумерные изображения хранятся в памяти в виде одномерных массивов. Обычно они записываются построчно: сначала идёт 0-я строка, затем 1-я и т.д.
Последовательный доступ к памяти осуществляется быстрее, чем произвольный. Это связано с работой кэша процессора, который помещает данные из памяти в кэш большими блоками, например, по 64 байта для современных процессоров. В этот блок попадают сразу несколько соседних по горизонтали пикселей. Значит, при обращении к последующим пикселям в той же строке скорость доступа будет выше, чем к последующим пикселям в столбце.
Решение: Обход по изображению нужно делать так, чтобы доступ к памяти был последовательный: во внешнем цикле производится обход по вертикали, а во внутреннем — по горизонтали:
for (int y = 0; y < image.Height(); y++)
for (int x = 0; x < image.Width(); x++)
...Примечание: В разных языках способ представления многомерных массивов в памяти может быть различным. Имейте это ввиду.
Ошибка 7. Путаница с шириной и высотой
Классическая проблема: тестирование либо отсутствует, либо осуществляется только на квадратных изображениях, в полевых условиях при работе с прямоугольными изображениями происходит выход за границу массива.
Решение: не забывайте про тестирование! Спор о TDD предлагаю не разводить: его использование — это личное дело каждого.
Ошибка 8. Отказ от абстракций
Боязнь плодить сущности — типичная ошибка новичков, она приводит к проблемам с читаемостью и восприятием кода. Здесь можно привести много примеров.
1. Обращение к пикселям через непосредственное вычисление индексов в массиве вместо использования методов getPixel(x, y) и setPixel(x, y). Помимо удобства, в этих методах можно проверять и корректно обрабатывать выход за границы изображения. Например, не выдавать ошибку, а эктраполировать значения изображения.
b1 = (float)0.25 * ( w1 - 1) * (w1 - 2) * (w1 + 1) * (h1 - 1) * (h1 - 2) * (h1 + 1);
b2 = -(float)0.25 * w1 * (w1 + 1) * (w1 - 2) * (h1 - 1) * (h1 - 2) * (h1 + 1);
b3 = -(float)0.25 * (w1 - 1) * (w1 - 2) * (w1 + 1) * (h1 + 1) * (h1 - 2);
b4 = (float)0.25 * w1 * h1 * (w1 + 1) * (w1 - 2) * (h1 + 1) * (h1 - 2);
b5 = -(1 / 12) * w1 * (w1 - 1) * (w1 - 2) * (h1 - 1) * (h1 - 2) * (h1 + 1);
b6 = -(1 / 12) * h1 * (w1- 1) * (w1 - 2) * (w1 + 1) * (h1 - 1) * (h1 - 2);
b7 = (1 / 12) * w1 * h1 * (w1 + 1) * (w1 - 2) * (h1 + 1) * (h1 - 2);
b8 = (1 / 12) * w1 * h1 * (w1- 1) * (w1 - 2) * (h1 - 1) *( h1 - 2);
b9 = (1 / 12) * w1 * (w1 - 1) * (w1 + 1) * (h1 - 1) * (h1 - 2) * (h1 + 1);
b10 = (1 / 12) * w1 * (w1 - 1) * (w1 - 2) * (w1 + 1) * (h1 - 1) * (h1+ 1);
b11 = (1 / 36) * w1 * h1 * (w1 - 1) * (w1 - 2) * (w1 - 1) * (h1 - 2) * (h1- 2);
b12 = -(1 / 12) * w1 * h1 * (w1 - 1) * (w1 + 1) * (h1 + 1) * (h1 - 2);
b13 = -(1 / 12) * w1 * h1 * (w1 + 1) * (w1 - 2) * (h1 - 1) * (h1 + 1);
b14 = -(1 / 36) * w1 * (w1 - 1) * (w1 + 1) * (h1 - 1) * (h1 - 2);
b15 = -(1 / 36) * w1 * h1 * (w1 - 1) * (w1 - 2) * (h1 - 1) * (h1 + 1);
b16 = (1 / 36) * w1 * h1 * (w1 - 1) * (w1 + 1) * (h1 - 1) * (h1 + 1);
image2.rawdata[y1 * image2.Width + x1].b =
image1.rawdata[h * image1.Width + w].b * b1
+ image1.rawdata[h * image1.Width + w + 1].b * b2
+ image1.rawdata[(h + 1) * image1.Width + w].b * b3
+ image1.rawdata[(h + 1) * image1.Width + w + 1].b * b4
+ image1.rawdata[h * image1.Width + w - 1].b * b5
+ image1.rawdata[(h - 1) * image1.Width + w].b * b6
+ image1.rawdata[(h + 1) * image1.Width + w - 1].b * b7
+ image1.rawdata[(h - 1) * image1.Width + w + 1].b * b8
+ image1.rawdata[h * image.Width + w + 2].b * b9
+ image1.rawdata[(h + 2) * image1.Width + w].b * b10
+ image1.rawdata[(h - 1) * image1.Width + w - 1].b * b11
+ image1.rawdata[(h + 1) * image1.Width + w + 2].b * b12
+ image1.rawdata[(h + 2) * image1.Width + w + 1].b * b13
+ image1.rawdata[(h - 1) * image1.Width + w + 2].b * b14
+ image1.rawdata[(h + 2) * image1.Width + w - 1].b * b15
+ image1.rawdata[(h + 2) * image1.Width + w + 2].b * b16;
image2.rawdata[y1 * image2.Width + x1].g =
image1.rawdata[h * image1.Width + w].g * b1
+ image1.rawdata[h * image1.Width + w + 1].g * b2
+ image1.rawdata[(h + 1) * image1.Width + w].g * b3
+ image1.rawdata[(h + 1) * image1.Width + w + 1].g * b4
+ image1.rawdata[h * image1.Width + w - 1].g * b5
+ image1.rawdata[(h - 1) * image1.Width + w].g * b6
+ image1.rawdata[(h + 1) * image1.Width + w - 1].g * b7
+ image1.rawdata[(h - 1) * image1.Width + w + 1].g * b8
+ image1.rawdata[h * image1.Width + w + 2].g * b9
+ image1.rawdata[(h + 2) * image1.Width + w].g * b10
+ image1.rawdata[(h - 1) * image1.Width + w - 1].g * b11
+ image1.rawdata[(h + 1) * image1.Width + w + 2].g * b12
+ image1.rawdata[(h + 2) * image1.Width + w + 1].g * b13
+ image1.rawdata[(h - 1) * image1.Width + w + 2].g * b14
+ image1.rawdata[(h + 2) * image1.Width + w - 1].g * b15
+ image1.rawdata[(h + 2) * image1.Width + w + 2].g * b16;
image2.rawdata[y1 * image2.Width + x1].r =
image1.rawdata[h * image1.Width + w].r * b1
+ image1.rawdata[h * image1.Width + w + 1].r * b2
+ image1.rawdata[(h + 1) * image1.Width + w].r * b3
+ image1.rawdata[(h + 1) * image1.Width + w + 1].r * b4
+ image1.rawdata[h * image1.Width + w - 1].r * b5
+ image1.rawdata[(h - 1) * image1.Width + w].r * b6
+ image1.rawdata[(h + 1) * image1.Width + w - 1].r * b7
+ image1.rawdata[(h - 1) * image1.Width + w + 1].r * b8
+ image1.rawdata[h * image1.Width + w + 2].r * b9
+ image1.rawdata[(h + 2) * image1.Width + w].r * b10
+ image1.rawdata[(h - 1) * image1.Width + w - 1].r * b11
+ image1.rawdata[(h + 1) * image1.Width + w + 2].r * b12
+ image1.rawdata[(h + 2) * image1.Width + w + 1].r * b13
+ image1.rawdata[(h - 1) * image1.Width + w + 2].r * b14
+ image1.rawdata[(h + 2) * image1.Width + w - 1].r * b15
+ image1.rawdata[(h + 2) * image1.Width + w + 2].r * b16;Это реализация бикубической интерполяции в исполнении студента.
Лишь немногие студенты догадались, что бикубическая интерполяция сепарабельна, и сумели обойтись четырьмя коэффициентами вместо шестнадцати.
2. Дублирование кода при работе с цветными изображениями, приводящее к ошибкам (см. пример выше). Вместо copy-paste кода и замены r на g и на b достаточно было бы использовать перегрузку операторов. В три раза меньше кода, в три раза понятнее.
3. Использование двумерных массивов вместо создания отдельного класса для изображения.
Проблема заключается в том, что индексация получается неестественной — (y, x) вместо (x, y), а размерности массива не очевидны: непонятно, что из GetLength(0) и GetLength(1) есть ширина, а что — высота. Высок риск просто перепутать индексы.
4. Использование трёхмерных массивов для хранения цветных изображений вместо создания отдельного класса для изображения. В дополнение к предыдущему пункту, приходится помнить, какой из индексов соответствует какой цветовой компоненте. Также видел, как трёхмерные массивы используются для хранения векторов, как в виде (vx, vy), так и в виде (v, angle). Запутаться легко.
5. Использование массива вместо класса. Угадайте, что возвращает следующая функция?
public static double[] HoughTransform2(GrayscaleFloatImage image, ref float[][] direction, ColorFloatImage cimage)Ответ: массив из 11 элементов, каждый из элементов имеет свой сакральный смысл, непонятный без длительного анализа кода. Не делайте так! Заведите класс и назовите каждое из полей по-человечески.
6. Переиспользование переменных с изменением семантики. Видите в коде gradx и grady и думаете, что это призводные по x и по y? А вот и нет, это модуль и угол:
gradx[x, y] = (float)Math.Sqrt(temp1 * temp1 + temp2 * temp2);
grady[x, y] = (float)(Math.Abs(Math.Atan2(temp2, temp1)) * 180 / Math.PI);Решение: никаких магических констант и индексов быть не должно. Оформляйте изображения как отдельные классы, сами пиксели тоже должны быть типизированы, а доступ к пикселям должен осуществляться только через специальные методы.
Ошибка 9. Применение некоторых математических функций неправильно или не к месту
Здесь виной всему слабое понимание архитектуры процессора, набора инструкций и времени их выполнения. Простительно, приходит с опытом, но некоторые моменты я отмечу:
1. Возведение в квадрат в виде Math.Pow(x, 2) или pow(x, 2) вместо x * x.
Компиляторы не оптимизируют эти конструкции, вместо однотактового умножения они генерируют довольно сложный код, включающий в себя вычисление экспоненты и логарифма, что приводит к снижению скорости на порядок-два.
Вызов pow(x, y) разворачивается в exp(log(x) * y). Это занимает около 300 тактов при использовании команд x87. В SSE же экспоненты и логарифма до сих пор нет, существует множество реализаций exp и log с различной производительностью, например, вот. В лучшем случае возведение в степень займёт 30–50 тактов. На умножение же уйдёт всего один такт.
2. Взятие целой части как (int)Math.Floor((float)(j) / k), причём k — вещественное и не меняется внутри цикла.
Здесь достаточно было бы написать (int)(j / k), а ещё лучше (int)(j * inv_k), где float inv_k = 1.0f / k.
Дело в том, что floor возвращает вещественное число, которое затем нужно дополнительно преобразовывать в целое. Получается лишняя довольно дорогая операция. Ну, а замена деления на умножение — просто оптимизация, операция деления до сих пор дорогая.
(int)floor(x) и (int)x зквивалентны только при неотрицательных x. Функция floor всегда округляет вниз, тогда как (int)x — в сторону нуля.
3. Вычисление обратного значения.
double _sum = pow(sum, -1);Зачем так делать, когда можно написать _sum = 1.0 / sum?
Решение: применяйте математические функции только там, где они нужны.
Ошибка 10. Незнание языка
И опять проблемы с математикой:
1. Путаница с типами. Использование long long для индексов пикселей вместо int, постоянные преобразования между float, double и int. Например, зачем писать (float)(1.0 / 16), когда можно написать 1.0f / 16.0f?
2. Вычисление полярного угла через возню с atan и проблемой с делением на ноль вместо использования atan2, которая делает именно то, что надо.
3. Необычная экспонента и магические константы:
g=(float)Math.pow(2.71,-(d*d)/(2*sigma*sigma));
t=((float)1/((float)Math.sqrt(6.28)*sigma));Здесь студент просто забыл про существование функции exp и константы pi. А вместо (float)1 можно просто написать 1.0f.
Решение: программируйте больше, только так вы наберётесь опыта.
Ошибка 11. Обфускация кода
Начинающие программисты любят показать своё мастерство, предпочитая писать короткий код, а не понятный.
1. Сложные циклы
for (int x1 = x - 1, x2 = 0; x1 <= x + 1; x1++, x2++)
{
for (int y1 = y - 1, y2 = 0; y1 <= y + 1; y1++, y2++)
{Здесь правильно было бы сделать цикл от -1 до 1, а x1 и x2 вычислять уже внутри цикла, ну и порядок поменять:
for (int j = -1; j <= 1; j++)
{
int y1 = y + j, y2 = j + 1;
for (int i = -1; i <= 1; i++)
{
int x1 = x + i, x2 = i + 1;Получилось бы даже быстрее за счёт того, что компиляторы легко оптимизируют простые циклы.
2. Крутые функции
long long ksize = llround(fma(ceil(3 * sigma), 2, 1)), rad = ksize >> 1;А нормальные люди просто напишут
int rad = (int)(3.0f * sigma);
int ksize = 2 * rad + 1;А это вообще за гранью добра и зла:
kernel[idx] = exp(ldexp(-pow(_sigma * (rad - idx), 2), -1));Для тех, кто не понял: ldexp(x, -1) — это просто деление на 2.
Решение: просто помните, что рано или поздно вам отобьют пальцы молотком за такой код.
Ошибка 12. Порча значений обрабатываемых изображений
Вот кусок кода из подавления немаксимумов, являющегося частью алгоритма Канни:
for x in xrange(grad.shape[0]):
for y in xrange(grad.shape[1]):
if ((angle[x, y] == 0) and ((grad[x, y] <= grad[getinds(grad, x + 1, y)])
or (grad[x, y] <= grad[getinds(grad, x - 1, y)]))) or\
((angle[x, y] == 0.25) and ((grad[x, y] <= grad[getinds(grad, x + 1, y + 1)])
or (grad[x, y] <= grad[getinds(grad, x - 1, y - 1)]))) or\
((angle[x, y] == 0.5) and ((grad[x, y] <= grad[getinds(grad, x, y + 1)])
or (grad[x, y] <= grad[getinds(grad, x, y - 1)]))) or\
((angle[x, y] == 0.75) and ((grad[x, y] <= grad[getinds(grad, x + 1, y - 1)])
or (grad[x, y] <= grad[getinds(grad, x - 1, y + 1)]))):
grad[x, y] = 0Здесь некоторые значения зануляются grad[x, y] = 0, а на последующих итерациях циклах к ним происходит обращение. Ошибка бы не произошла, если бы для вычисления промежуточного результата создавалось новое изображение, а не перезаписывалось текущее.
Решение: не стремитесь экономить память раньше времени, подумайте о функциональной парадигме.
Остальные ошибки
Остальные ошибки уже имеют непрограммистский характер. Это ошибки в реализации алгоритмов вследствие их непонимания, они индивидуальны. Например, неверный выбор размера ядра для фильтра Гаусса.
Фильтр Гаусса — один из основных фильтров в обработке изображений. Он лежит в основе огромного числа алгоритмов: детектирование контуров (edges) и хребтов (ridges), поиск ключевых точек, повышение резкости и т.д. Фильтр Гаусса имеет параметр «сигма», определяющий уровень размытия, его ядро описывается формулой:
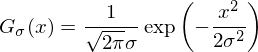
а график имеет вид:
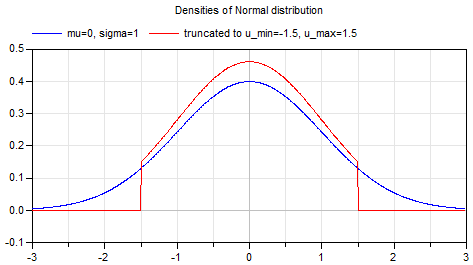
Данная функция нигде не обращается в ноль, а свёртка с ядром бесконечного размера не имеет смысла. Поэтому размер ядра выбирается таким, чтобы ошибка была ничтожно мала. Для практических задач достаточно взять ядро с радиусом (int)(3 * sigma) — ошибка будет меньше 1/1000. Выбор слишком маленького ядра (красная функция на графике выше) приведёт к искажению фильтра Гаусса. Использование ядра фиксированного размера, например, 5×5 и приводит к некорректным результатам уже при sigma = 1.5.
Итог: общие рекомендации для начинающих работать с изображениями
- Не используйте системные объекты Bitmap, HBITMAP и им подобные.
- Прежде, чем использовать библиотеки для работы с изображениями, начните с написания велосипедов, а уже затем бросайтесь в бой.
- Используйте тип float для хранения значений пикселей. Не занимайтесь преждевременной оптимизацией по скорости и памяти, заменяя float на byte.
- При преобразовании из float в byte помните об ошибках округления и выход за границы типа.
- Помните об отрицательных значениях.
- Совершайте обход по пикселям изображения в правильном порядке.
- Тщательно тестируйте код.
- Не бойтесь плодить сущности. Код должен быть понятным.
- Используйте математические операции с умом.
- Учите язык.
- Не пытайтесь показать мастерство.
- Читайте учебники по обработке изображений — там много всего полезного пишут.
Для облегчения написания программ я создал проекты, в которых уже реализовано чтение и запись изображений, созданы классы для хранения изображений с минимально возможным функционалом и приведён пример операции над изображениями:
→ Visual Studio 2015, C++
→ Visual Studio 2015, C#
Версий под Linux нет — студенты, использующие Linux, обычно не испытывают проблем с такими вещами.
Ну и на закуску — просто картинки.
Выделение контуров с помощью алгоритма Канни. Слева вверху — входное изображение, второе слева — правильный результат, остальное — ошибочные результаты.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Увеличение с помощью бикубической интерполяции.
 |
 |
 |
 |
 |
Комментарии (1)
16 января 2017 в 12:56
0↑
↓
зачем писать (float)(1.0 / 16), когда можно написать 1.0f / 16.0f
можно еще проще:1.f / 16
, а в c#:1f / 16
