[Из песочницы] Software renderer — 1: матчасть
Программный рендеринг (software rendering) — это процесс построения изображения без помощи GPU. Этот процесс может идти в одном из двух режимов: в реальном времени (вычисление большого числа кадров в секунду — необходимо для интерактивных приложений, например, игр) и в «оффлайн» режиме (при котором время, которое может быть потрачено на вычисление одного кадра, не ограничено настолько строго — вычисления могут длиться часы или даже дни). Я буду рассматривать только режим рендеринга в реальном времени.У этого подхода существуют как недостатки так и достоинства. Очевидным недостатком является производительность — CPU не в состоянии конкурировать с современными видеокартами в этой области. К достоинствам стоит причислить независимость от видеокарты — именно поэтому он используется как замена аппаратного рендеринга в случаях, когда видеокарта не поддерживает ту или иную возможность (так называемый software fallback). Существуют и проекты, цель которых — полностью заменить аппаратный рендеринг программным, например, WARP, входящий в состав Direct3D 11.
Но главным плюсом является возможность написания подобного рендерера самостоятельно. Это служит образовательным целям и, на мой взгляд, это — самый лучший способ понять лежащие в основе алгоритмы и принципы.
Это именно то, о чем будет рассказано в серии этих статей. Мы начнем с возможности закрашивать пиксель в окне заданным цветом и построим на этом возможность отрисовки трехмерной сцены в реальном времени, с движущимися текстурированными моделями и освещением, а так же с возможностью перемещаться по этой сцене.
Но для того, чтобы вывести на экран хотя бы первый полигон, необходимо освоить математику, на которой это построено. Первая часть будет посвящена именно ей, поэтому в много различных матриц и прочей геометрии.
В конце статьи будет ссылка на гитхаб проекта, который можно рассматривать как пример реализации.Несмотря на то, что статья будет описывать самые основы, читателю все же необходим определенный фундамент для ее понимания. Этот фундамент: основы тригонометрии и геометрии, понимание декартовых систем координат и базовые операции над векторами. Так же, хорошей идеей будет прочтение какой-либо статьи об основах линейной алгебры для разработчиков игр (например, этой), поскольку я буду пропускать описания некоторых операций и останавливаться только на самых, с моей точки зрения, важных. Я постараюсь показать, при помощи чего делается вывод некоторых важных формул, но не буду расписывать их детально — полные доказательства можно сделать самому или найти в соответствующей литературе. По ходу статьи я сначала постараюсь давать алгебраические определения того или иного понятия, а затем уже описывать их геометрическую интерпретацию. Большая часть примеров будет в двухмерном пространстве, поскольку мои навыки рисования трехмерных и, тем более, четырехмерных пространств оставляют желать лучшего. Тем не менее, все примеры легко обобщаются на пространства других размерностей. Все статьи будут в большей степени ориентированы на описание алгоритмов, а не на их реализацию в коде.
ВектораВектор — одно из ключевых понятий в трехмерной графике. И хотя линейная алгебра дает ему очень абстрактное определение, в рамках наших задач под n-мерным вектором мы можем понимать просто массив из n действительных чисел: элемент пространства Rn: 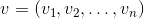
Интерпретация этих чисел зависит от контекста. Две самые частые: эти числа задают координаты точки в пространстве или же направленное смещение. Несмотря на то, что их представление одинаково (n действительных чисел), их концепции различаются — точка описывает положение в системе координат, а смещение не имеет положения как такового. В дальнейшем, мы так же можем определять точку с помощью смещения, подразумевая, что смещение происходит от начала координат.
Как правило, в большинстве игровых и графических движков присутствует класс вектора именно как набора чисел. Смысл же этих чисел зависит от контекста, в котором они используются. В этом классе определены методы как для работы с геометрическими векторами (например, вычисление векторного произведения) так и с точками (например, вычисление расстояния между двумя точками).
Во избежание путаницы, в рамках статьи мы не будем больше понимать под словом «вектор» абстрактный набор чисел, а будем так называть смещение.
Скалярное произведение
Единственная операция над векторами, на которой я хочу остановиться подробно (ввиду ее фундаментальности) — это скалярное произведение. Как ясно из названия, результат этого произведения — скаляр, и определяется он по следующей формуле: 
У скалярного произведения есть две важные геометрические интерпретации.
Измерение угла между векторами.Рассмотрим следующий треугольник, полученный из трех векторов: 
Записав для него теорему косинусов и сократив выражение, придем к записи:

Поскольку длина ненулевого вектора по определению больше 0, то косинус угла определяет знак скалярного произведения и его равенство нулю. Получаем (считая, что угол от 0 до 360 градусов):

Скалярное произведение вычисляет длину проекции вектора на вектор.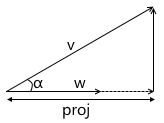
Из определения косинуса угла получаем:
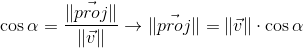
Мы так же уже знаем из предыдущего пункта, что:

Выразив из второго выражения косинус угла, подставив в первое и домножив на ||w||, получаем результат:
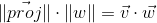
Таким образом, скалярное произведение двух векторов равно длине проекции вектора v на вектор w, умноженное на длину вектора w. Часто встречающийся частный случай этой формулы — w имеет единичную длину и, следовательно, скалярное произведение вычисляет точную длину проекции.
Эта интерпретация очень важна, поскольку она показывает, что скалярное произведение вычисляет координаты точки (заданной вектором v, подразумевая смещение от начала координат) вдоль заданной оси. Самый простой пример:

Мы в дальнейшем воспользуемся этим при построении трансформации в систему координат камеры.
Системы координат Этот раздел призван подготовить основу для введения матриц. Я, на примере мировой и локальной систем, покажу, по каким причинам используются несколько систем координат, а не одна, и о том, как описать одну систему координат относительно другой.Представим, что у нас возникла необходимость в отрисовке сцены с двумя моделями, например:
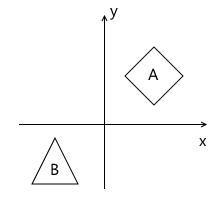
Какие системы координат естественным образом вытекают из такой постановки? Первая — это система координат самой сцены (которая изображена на рисунке). Это система координат, описывающая мир, который мы собираемся рисовать — именно поэтому она и называется «мировой» (на картинках будет обозначена словом «world»). Она «связывает» все объекты сцены вместе. Например, координаты центра объекта A в этой система координат — (1, 1), а координаты центра объекта B — (-1, -1).
Таким образом, одна система координат уже есть. Теперь необходимо подумать о том, в каком виде к нам приходят модели, которые мы будем использовать в сцене.
Для простоты будем считать, что модель описывается просто списком точек («вершин») из которых она состоит. Например, модель B состоит из трех точек, которые приходят нам в следующем формате:
v0 = (x0, y0)v1 = (x1, y1)v2 = (x2, y2)На первый взгляд, было бы здорово, если бы они уже были описаны в нужной нам «мировой» системе! Представляете, вы добавляете модель на сцену, а она уже находится там, где нам и нужно. Для модели B это могло бы выглядеть вот так:
v0 = (-1.5, -1.5)v1 = (-1.0, -0.5)v2 = (-0.5, -1.5)Но использовать такой подход не выйдет. На то есть важная причина: это лишает возможности использовать одну и ту же модель заново в разных сценах. Представьте, что вам дали модель B, которая была смоделирована так, что при добавлении ее на сцену она оказывается в нужном нам месте, как в примере выше. Затем, внезапно, требование изменилось — мы хотим ее сдвинуть совсем на другую позицию. Получается, человеку, который создал эту модель, придется двигать ее самостоятельно и затем опять отдавать вам. Конечно, это — полный абсурд. Еще более сильный аргумент это то, что в случае с интерактивными приложениями, модель может двигаться, поворачиваться, анимироваться на сцене — что же, художнику делать модель во всех возможных положениях? Это звучит еще более глупо.
Решение этой проблемы — «локальная» система координат модели. Мы моделируем объект таким образом, чтобы его центр (или то, что можно условно за таковой принять) был расположен в начале координат. Затем мы программно ориентируем (перемещаем, поворачиваем и т.д.) локальную систему координат объекта в нужное нам положение в мировой системе. Возвращаясь к сцене выше, объект A (единичный квадрат, повернутый на 45 градусов по часовой стрелке) может быть смоделирован следующим образом:

Описание модели в этом случае будет выглядеть следующим образом:
v0 = (-0.5, 0.5)v1 = (0.5, 0.5)v2 = (0.5, -0.5)v3 = (-0.5, -0.5)И, соответственно, положение в сцене двух систем координат — мировой и локальной объекта A:

Это — один из примеров, почему наличие нескольких систем координат упрощает жизнь разработчикам (и художникам!). Есть еще и другая причина — переход к другой системе координат может упростить необходимые вычисления.
Описание одной системы координат относительно другой Не существует такого понятия как «абсолютные координаты». Описание чего-либо всегда происходит относительно какой-то системы координат. В том числе и описание другой системы координат.Мы можем построить своеобразную иерархию систем координат в примере выше:
— world space — local space (object A) — local space (object B) В нашем случае эта иерархия очень проста, но в реальных ситуациях она может иметь гораздо более сильное ветвление. Например, у локальной системы координат объекта могут быть дочерние системы отвечающие за положение той или иной части тела.Каждая дочерняя система координат может быть описана относительно родительской при помощи следующих значений:
точка начала координат дочерней системы относительно родительской
координаты базисных векторов дочерней системы относительно родительской
Например, в картинке ниже, начало координат системы x’y' (обозначенное как O') расположено в точке (1, 1), а координаты ее базисных векторов i' и j' равны (0.7, -0.7) и (0.7, 0.7) соответственно (что приблизительно соответствует осям, повернутым на 45 градусов по часовой стрелке).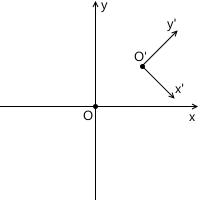
Нам не нужно описывать мировую систему координат относительно какой-либо другой, потому что мировая система — корень иерархии, нас не волнует где она расположена или как она ориентирована. Поэтому для ее описания мы используем стандартный базис:
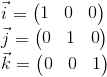
Перевод координат точек из одной системы в другую
Координаты точки P в родительской системе координат (обозначим как Pparent) могут быть вычислены при помощи координат этой точки в дочерней системе (обозначим как Pchild) и ориентации этой дочерней системы относительно родительской (описаной с помощью начала координат Ochild и базисных векторов i' и j') следующим образом: 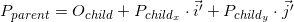
Снова вернемся к примеру сцены выше. Мы сориентировали локальную систему координат объекта A относительно мировой:

Как мы уже знаем, в процессе отрисовки нам необходимо будет перевести координаты вершин объекта из локальной системы координат в мировую. Для этого нам необходимо описание локальной системы координат относительно мировой. Выглядит оно следующим образом: начало координат в точке (1, 1), а координаты базисных векторов равны (0.7, -0.7) и (0.7, 0.7) (способ расчета координат базисных векторов после поворота будет описан позже, пока что нам достаточно результата).
Для примера возьмем первую вершину v = (-0.5, 0.5) и вычислим ее координаты в мировой системе:
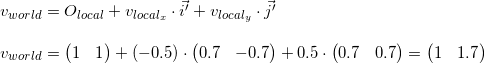
В верности результата можно убедиться, посмотрев на изображение выше.
Матрицы
Матрица размерности m x n — соответствующей размерности таблица чисел. Если количество столбцов в матрице равно количеству строк, то матрица называется квадратной. Например, матрица 3×3 выглядит следующим образом: 
Перемножение матриц
Предположим, что у нас есть две матрицы: M (размерностью a x b) и N (размерностью c x d). Выражение R = M · N определено только в том случае, если количество столбцов в матрице M равно числу строк в матрице N (т.е. b = c). Размерность полученной матрицы будет равна a x d (т.е. количество строк равно кол-ву строк M, а число столбцов — числу столбцов в N), а значение, находящееся на позиции ij, вычисляется как скалярное произведение i-й строки M на j-й столбец N: 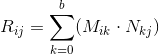
Если результат умножения двух матриц M · N определен, то это вовсе не значит, что определено и умножение в обратную сторону — N · M (могут не совпадать кол-во строк и столбцов). В общем случае, операция умножения матриц так же не коммутативна: M · N ≠ N · M.
Единичная матрица — это матрица, которая не изменяет домноженную на нее другую матрицу (т.е. M · I = M) — своеобразный аналог единицы для обычных чисел:
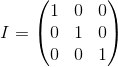
Представление векторов в виде матриц Мы так же можем представить вектор как матрицу. Есть два возможных способа это сделать, которые называют ''вектор-строка'' и ''вектор-столбец''. Как понятно из название, вектор-строка — это вектор, представленный в виде матрицы с одной строкой, а вектор-столбец — вектор, представленный в виде матрицы с одним столбцом.Вектор-строка:
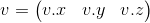
Вектор-столбец:

Далее мы очень часто будем сталкиваться с операцией умножения матрицы на вектор (для чего — будет обьяснено в следущем разделе), и, забегая вперед, матрицы с которыми мы будем работать будут иметь размерность либо 3×3 либо 4×4.
Рассмотрим, каким способом мы можем умножить трехмерный вектор на матрицу 3×3 (аналогичные рассуждения применяются для других размерностей). Согласно определению, две матрицы могут быть перемножены, если количество столбцов первой матрицы равняется количеству строк второй. Таким образом, поскольку мы можем представить вектор и как матрицу 1×3 (вектор-строка) и как матрицу 3×1 (вектор-столбец), мы получаем два возможных варианта:
Умножение вектора на матрицу «слева»: 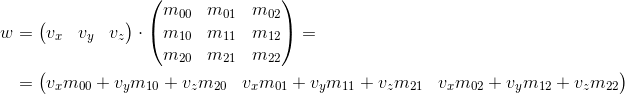
Умножение вектора на матрицу «справа»: 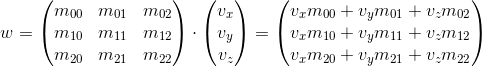
Как видно, мы получаем разный результат в каждом из случаев. Это может привести к случайным ошибкам, если API позволяет умножать вектор на матрицу с обоих сторон, поскольку, как мы увидим в дальнейшем, матрица трансформации подразумевает что вектор будет умножен на нее одним из двух способов. Так что, по моему мнению, в API лучше придерживаться только одного из двух вариантов. В рамках этих статей я буду использовать первый вариант — т.е. вектор умножается на матрицу слева. Если вы решили использовать другой порядок, то, для того чтобы получить корректные результаты, вам нужно будет транспонировать все матрицы, которые в дальнейшем встретятся в этой статье, а слово «строка» заменить на «столбец». Это так же влияет на порядок умножения матриц при наличии нескольких трансформаций (подробнее будет рассмотрено далее).Из результата умножения так же видно, что матрица определенным образом (зависящем от значения ее элементов) изменяет вектор, который был на нее домножен. Это могут быть такие трансформации как поворот, масштабирование и другие.
Еще одно крайне важное свойство операции умножения матриц, которое нам в дальнейшем пригодится — дистрибутивность относительно сложения:
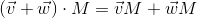
Геометрическая интерпретация Как мы увидели в предыдущем разделе — матрица определенным образом трансформирует домноженный на нее вектор.Еще раз вспомним, что любой вектор может быть представлен как линейная комбинация базисных векторов:
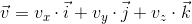

Умножим это выражение на матрицу:
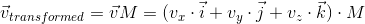
Используя дистрибутивность относительно сложения, получим:

Мы уже видели подобное ранее, когда рассматривали, как перевести координаты точки из дочерней системы в родительскую, тогда это выглядело следующим образом (для трехмерного пространства):
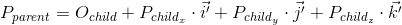
Между этими двумя выражениями есть два различия — в первом выражении нет перемещения (Ochild, мы рассмотрим позже этот момент подробнее, когда будем говорить о линейных и афинных трансформациях), а вектора i', j' и k' заменены на iM, jM и kM соответственно. Следовательно, iM, jM и kM — есть базисные вектора дочерней системы координат и мы переводим точку vchild (vx, vy, vy) из этой дочерней системы координат в родительскую (vtransformed = vparentM).
Процесс трансформации можно изобразить следующим образом на примере вращения против часовой стрелки (xy — изначальная, родительская система координат, x’y' — дочерняя, полученная в результате трансформации):
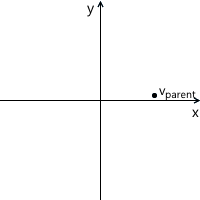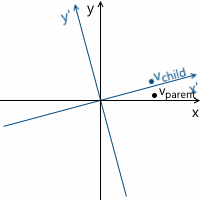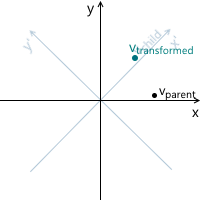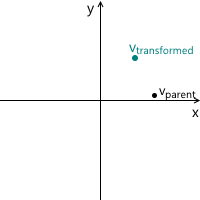
На всякий случай, чтобы убедиться, что нам понятен смысл каждого из векторов, используемых выше, перечислим их заново:
vparent — вектор, который мы изначально умножали на матрицу M. Его координаты описаны относительно родительской системы координат
vchild — вектор, координаты которого равны вектору vparent, но они описаны относительно дочерней системы координат. Это вектор vparent трансформированный тем же образом, что и базисные вектора (поскольку мы используем те же координаты)
vtransformed — тот же самый вектор, что и vchild, но с координатами пересчитанными относительно родительской системы координат. Это итоговый результат трансформации вектора vparent
Теперь рассмотрим, что происходит при умножении базисных векторов на матрицу M: 
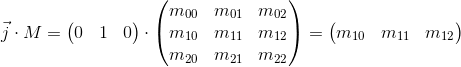
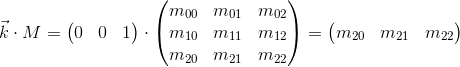
Видно, что базисные вектора новой дочерней системы координат, полученной в результате умножения на матрицу M, совпадают со строками матрицы. Это и есть та самая геометрическая интерпретация, которую мы искали. Теперь, увидев матрицу трансформации, мы будем знать куда смотреть, чтобы понять что она делает — достаточно представить ее строки как базисные вектора новой системы координат. Трансформация, происходящая с системой координат, будет та же что и трансформация, происходящая с вектором, домноженным на эту матрицу.
Мы так же можем комбинировать трансформации, представленные в виде матриц, при помощи умножения их друг на друга:
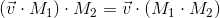
Таким образом, матрицы представляют собой очень удобный инструмент для описания и комбинирования трансформаций.
Линейные трансформации
Для начала рассмотрим самые часто используемые линейные трансформации. Линейная трансформация — это трансформация, которая удовлетворяет двум свойствам: 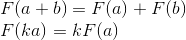
Важное следствие — линейная трансформация не может содержать перемещения (это так же является причиной, по которой слагаемое Ochild отсутствовало в предыдущем разделе), поскольку, согласно второй формуле, 0 всегда отображается в 0.
Вращение
Рассмотрим вращение в двумерном пространстве. Это трансформация, которая поварачивает систему координат на заданный угол. Как мы уже знаем, нам достаточно вычислить новые координатные оси (полученные после вращения на заданный угол), и использовать их как строки матрицы трансформации. Результат легко получается из базовой геометрии: 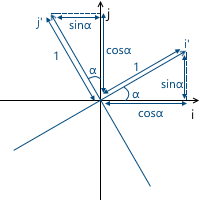

Пример:

Результат для вращения в трехмерном пространстве получается аналогичным образом, с той лишь разницей что мы вращаем плоскость составленную из двух координатных осей, и фиксируем третью (вокруг которой и происходит вращение). Например, матрица вращения вокруг оси x выглядит следующим образом:

Масштабирование
Мы можем изменить масштаб объекта относительно всех осей применив следующую матрицу: 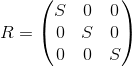
Оси трансформированной системы координат будут направлены так же, как и у изначальной системы координат, но будут требовать в S раз большей длины для одной единицы измерения:
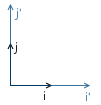
Пример: 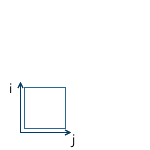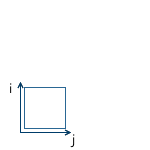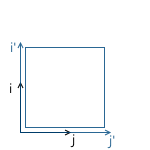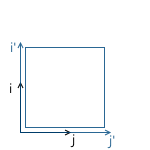
Масштабирование с одинаковым коэффициентом относительно всех осей называется равномерным (uniform). Но мы так же можем произвести масштабирование с разными коэффициентами вдоль разных осей (nonuniform):
Сдвиг
Как понятно из названия, эта трансформация производит сдвиг вдоль координатной оси, оставляя остальные оси нетронутыми: 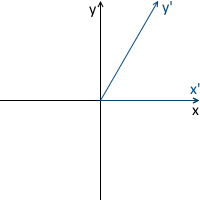
Соответственно, матрица сдвига оси y выглядит следующим образом:
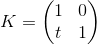
Пример:

Матрица для трехмерного пространства строится аналогичным образом. Например, вариант для сдвига оси x:

Несмотря на то, что эта трансформация используется очень редко, она пригодится нам в будущем, когда мы будем рассматривать афинные трансформации.
В нашем запасе уже есть приличное кол-во трансформаций, которые могут быть представлены как 3×3 матрица, но нам не хватает еще одной — перемещения. К несчастью, выразить перемещение в трехмерном пространстве при помощи 3×3 матрицы невозможно, поскольку перемещение не является линейной трансформацией. Решением этой проблемы являются однородные координаты, которые мы рассмотрим позже.
Центральная проекция Наша итоговая цель — изобразить трехмерную сцену на двухмерном экране. Таким образом, мы должны тем или иным способом спроектировать нашу сцену на плоскость. Существует две самые часто используемые типы проекций — ортографическая и центральная (другое название — перспективная).Когда человеческий глаз смотрит на трехмерную сцену, объекты, находящиеся дальше от него, становятся меньше в итоговом изображении, которое и видит человек — этот эффект называется перспективой. Ортографическая проекция игнорирует перспективу, что является полезным свойством при работе в различных САПР-системах (а так же в 2D играх). Центральная же проекция обладает этим свойством и потому добавляет значительную долю реалистичности. В этой статье мы будем рассматривать только ее.
В отличии от ортографической проекции, линии в перспективной проекции не параллельны друг другу, а пересекаются в точке, называемой центром проекции. Центром проекции выступает «глаз», которым мы смотрим на сцену — виртуальная камера:
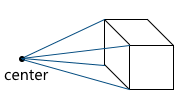
Изображение формируется на плоскости, находящейся на заданном расстоянии от виртуальной камеры. Соответственно, чем больше расстояние от камеры, тем больше размер проекции:

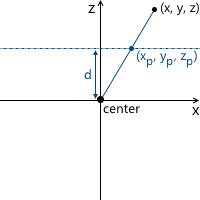
Рассмотрим самый простой пример: камера расположена в начале координат, а плоскость проекции находится на расстоянии d от камеры. Нам известны координаты точки, которую мы хотим спроецировать: (x, y, z). Найдем координату xp проекции этой точки на плоскость:
На этой картинке видны два подобных треугольника — CDP и CBA (по трем углам):
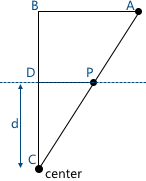
Соответственно, отношения между сторонами сохраняются:
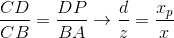
Получаем результат для x-координаты:
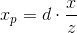
И, аналогично, для y-координаты:

Позже, нам необходимо будет использовать эту трансформацию для формирования спроецированного изображения. И тут возникает проблема — мы не можем представить деление на z-координату в трехмерном пространстве с помощью матрицы. Решением этой проблемы, так же как и в случае с матрицей перемещения, являются однородные (homogeneous) координаты.
Проективная геометрия и однородные координаты К текущему моменту мы столкнулись с двумя проблемами: Перемещение в трехмерном пространстве не может быть представлено как 3×3 матрица Перспективная проекция не может быть представлена в виде матрицы Обе эти проблемы решает использование однородных координат. Однородные координаты — понятие из проективной геометрии. Проективная геометрия изучает проективные пространства, и, чтобы понять геометрическую интерпретацию однородных координат, нужно с ними познакомиться.Ниже мы будем рассматривать определения для двухмерных проективных пространств, поскольку их легче изобразить. Аналогичные рассуждения применяются и для трехмерных проективных пространств (мы в дальнейшем будем использовать именно их).
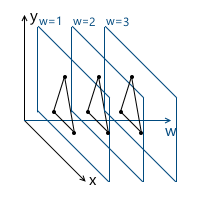
Определим луч в пространстве R3 следующим образом: луч — это множество векторов вида kv (k — скаляр, v — ненулевой вектор, элемент пространства R3). Т.е. вектор v задает направление луча:

Теперь мы можем перейти к определению проективного пространства. Проективная плоскость (т.е. проективное пространство с размерностью равной двум) P2, ассоциированная с пространством R3, это множество лучей в R3. Таким образом, «точка» в P2 — это луч в R3.
Соответственно, два вектора в R3 задают один и тот же элемент в P2, если один из них может быть получен домножением второго на какой-либо скаляр (поскольку в этом случае они лежат на одном луче):
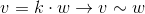
К примеру, вектора (1, 1, 1) и (5, 5, 5) представляют один и тот же луч, а значит являются одной и той же «точкой» в проективной плоскости.
Таким образом мы и пришли к однородным координатам. Каждый элемент в проективной плоскости задается лучом из трех координат (x, y, w) (последняя координата называется w вместо z — общепринятое соглашение) — эти координаты называются однородными и определены с точностью до скаляра. Это означает, что мы можем домножать (или делить) на скаляр однородные координаты, и они все равно будут представлять ту же самую «точку» в проективной плоскости.
В дальнейшем мы будем использовать однородные координаты для представления афинных (содержащих перемещение) трансформаций и проецирования. Но до этого нужно решить еще один вопрос: каким образом представить в виде однородных координат уже данные нам вершины модели? Поскольку «дополнение» до однородных координат происходит за счет добавления третьей координаты w, вопрос сводится к тому, какое значение w нам необходимо использовать. Ответ на этот вопрос — любое не равное нулю. Разница в использовании различных значений w заключается в удобстве работы с ними.
И, как будет понятно далее (и что отчасти ясно интуитивно), самым удобным значением w является единица. Преимущества этого выбора следующие:
Это позволяет в более естественном виде представить перемещение в виде матрицы (будет показано далее)
После некоторых трансформаций (включая перспективную проекцию) значение w будет произвольным, и нам нужно будет вернуться на выбранную нами изначально плоскость (т.е. вернуть изначально выбранное значение w): 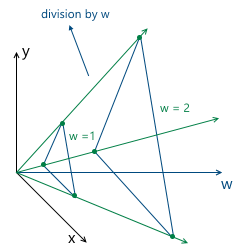
Если эта плоскость — w = 1, нам достаточно будет поделить все координаты на w — в результате, мы получим единицу в w координате
Таким образом, мы выбираем значение w = 1, а значит наши входные данные в однородных координатах теперь будут выглядить следующим образом (разумеется, единица уже добавлена будет нами, а не будет находиться в самом описании модели): v0 = (x0, y0, 1)v1 = (x1, y1, 1)v2 = (x2, y2, 1)Теперь нужно рассмотреть особый случай при работе с w-координатой. А именно — ее равенство нулю. Выше мы говорили, что мы можем выбрать любое значение w, не равное нулю, для расширения до однородных координат. Мы не может взять w = 0, в частности, потому, что это не позволит перемещать эту точку (поскольку, как мы увидим дальше, перемещение происходит именно за счет значения в w координате). Так же, если у точки координата w — нулевая, мы можем рассматривать ее как точку «в бесконечности», поскольку при попытке вернуться на плоскость w = 1 мы получим деление на ноль:
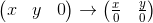
И, хотя мы не можем использовать нулевое значение для вершин модели, мы можем использовать его для векторов! Это приведет к тому, что вектор не будет подвержен перемещениям при трансформациях — что имеет смысл, ведь вектор не описывает положение. Например, при трансформации нормали мы не можем перемещать ее, иначе получим неверный результат. Мы рассмотрим это подробнее, когда возникнет необходимость в трансформации векторов.
В связи с этим, часто пишут, что при w = 1 мы описываем точку, а при w = 0 — вектор.
Как я уже писал, мы использовали пример двухмерных проективных проективных пространств, но в действительно будем использовать трехмерные проективные пространства, а значит каждая точка будет описываться 4-мя координатами: (x, y, z, w).
Перемещение с использование однородных координат
Теперь у нас есть все необходимые инструменты для описания афинных трансформаций. Афинные трансформации — линейные трансформации с последующим смещением. Они могут быть описаны следующим образом: 
Мы так же можем использовать 4×4 матрицы для описания афинных трансформаций, используя однородные координаты:
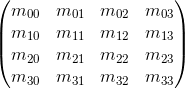
Рассмотрим результат умножения вектора, представленного в виде однородных координат, и умножения на 4×4 матрицу:
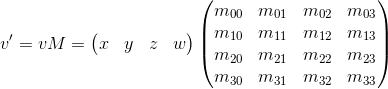
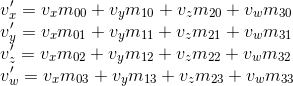
Как видно, отличие от трансформации, представленной в виде 3×3 матрица, состоит в наличии 4-й координаты, а так же новых слагаемых в каждой из координат вида vw · m3i. Используя это, и подразумевая w = 1, мы можем представить перемещение следующим образом:
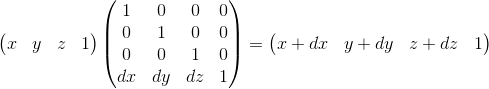
Тут можно убедиться в правильности выбора w = 1. Для представления смещения dx мы используем слагаемое вида w · dx / w. Соответственно, последняя строка матрицы выглядит как (dx/w, dy/w, dz/w, 1). В случае w = 1 мы можем просто опустить знаменатель.
У этой матрицы так же есть геометрическая интерпретация. Вспомним матрицу сдвига, которую мы рассматривала ранее. Она имеет в точности такой же формат, разница лишь в том, что происходит сдвиг четвертой оси, таким образом сдвигая трехмерное подпространство расположенное в гиперплоскости w = 1 на соответствующие значения.
Описание виртуальной камеры Виртуальная камера — это «глаз», которым мы смотрим на сцену. Прежде чем двигаться дальше, необходимо понять, каким образом можно описать положение камеры в пространстве, и какие параметры необходимы для формирования итогового изображения.Параметры камеры задают усеченную пирамиду обзора (view frustum), которая определяет, какая часть сцены попадет в итоговое изображение: