[Из песочницы] Reverse engineering тестового crackme от Лаборатории Касперского
Приветствую сообщество! Давным давно, в 2013 году на Хабре был опубликован пост «Reverse engineering на собеседовании: как мы нанимаем на работу». В нём был предложен тестовый crackme для претендентов на позицию вирусного аналитика. Убедившись, что полного разбора тестового файла в интернете нет, я решил написать свой разбор. И так, приступим. Crackme 64-разрядный. Запустим его в IDA Pro.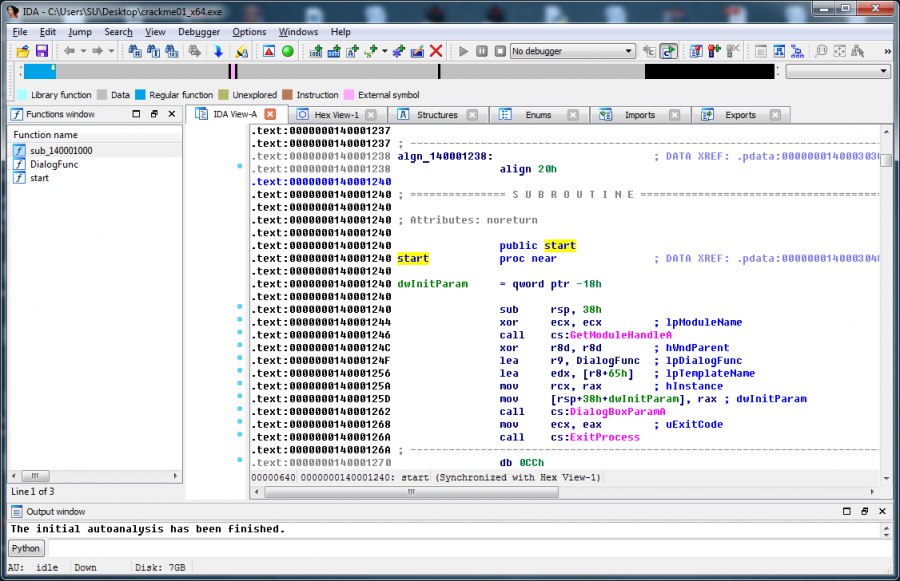
Видим слева в списке функций три функции: start — функция, с которой начинается выполнение программы, DialogFunc — эта функция общается с нами и некоторая функция sub_140001000. Рассмотрим диалоговую функцию. Декомпилируем её Hex Rays-ом.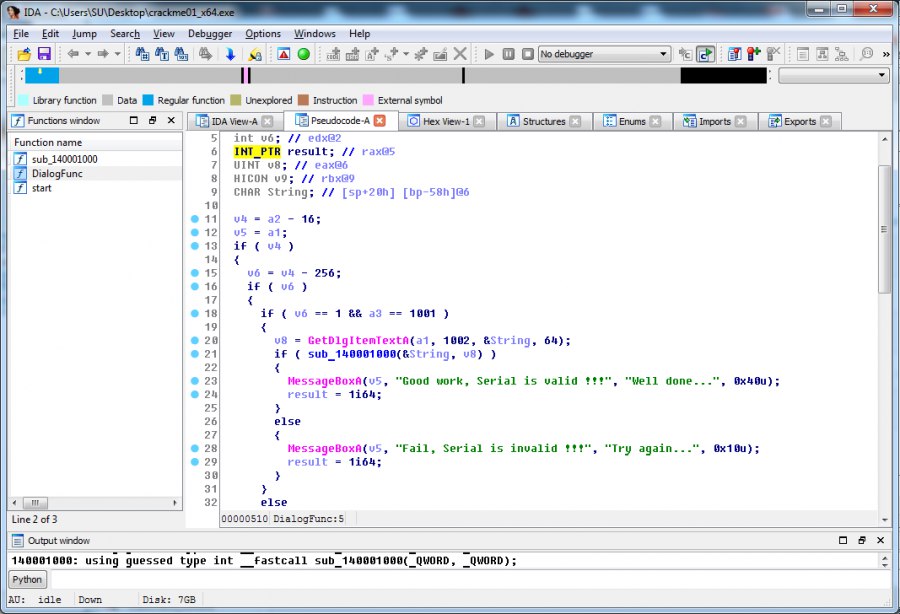
В глаза бросается ветвление условий, согласно которому, если некоторая функция sub_140001000 вернет TRUE, то появится сообщение, информирующее нас о отлично проделанной работе, иначе неверно. Разберем нашу заветную функцию sub_140001000. Если мы пропустим её через декомпилятор, то увидим, что в качестве аргумента передается указатель всего на одно значение. Вероятно, это значение берется из диалогового окна и является вводимым ключом. Теперь рассмотрим ассемблерный листинг. Имеется первая проверка условия верности введенных данных. Если условие выполняется, то программа исполняется дальше, если не выполняется, то идет возврат из подпрограммы.
Запустим наш crackme под отладчиком. Воспользуемся x64dbg. Поставим breakpoint на нашей первой проверке. В качестве вводимого ключа используем набор цифр 1234567.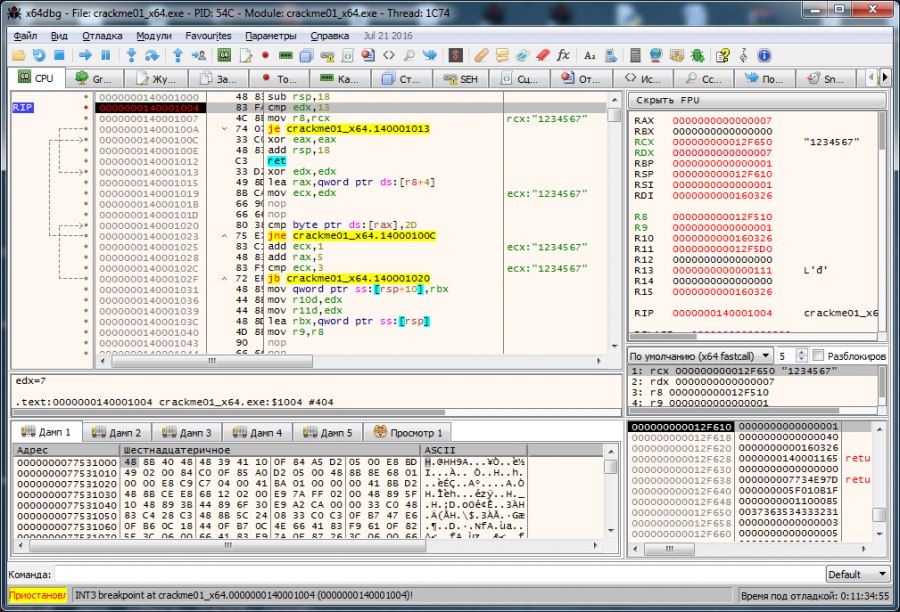
Как видно, происходит проверка значения регистра edx и числа 13h (в десятичной системе исчисления это 19). Вероятно, это проверка на количество введенных знаков ключа (у нас их 7 и в регистре edx число 7). Попробуем ввести другое количество символов. Запустим отладчик заново. Введем 9 цифр 123456789.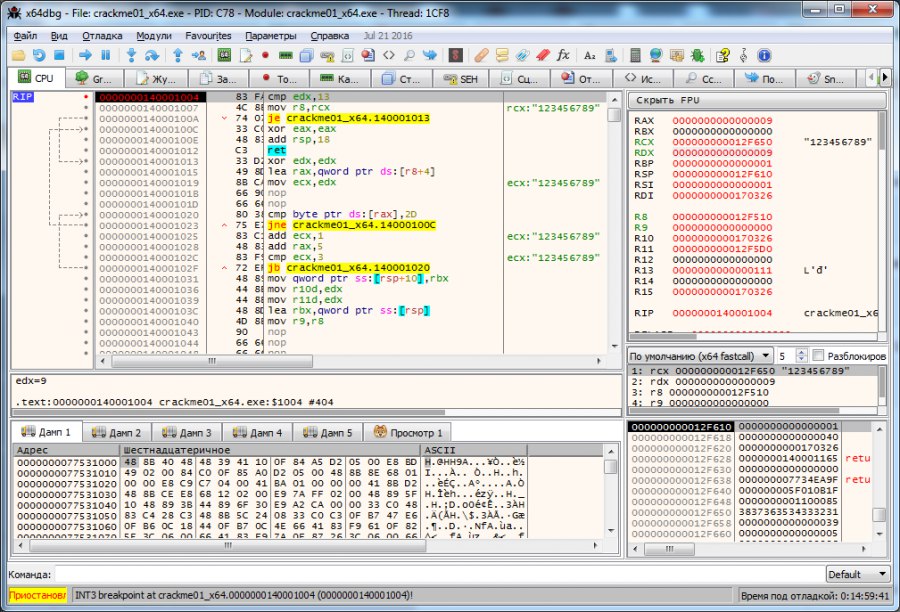
Похоже, что так оно и есть. Значит наш ключ должен содержать 19 символов. Вводим 19 символов 1234567890123456789 и переходим к следующему этапу проверки.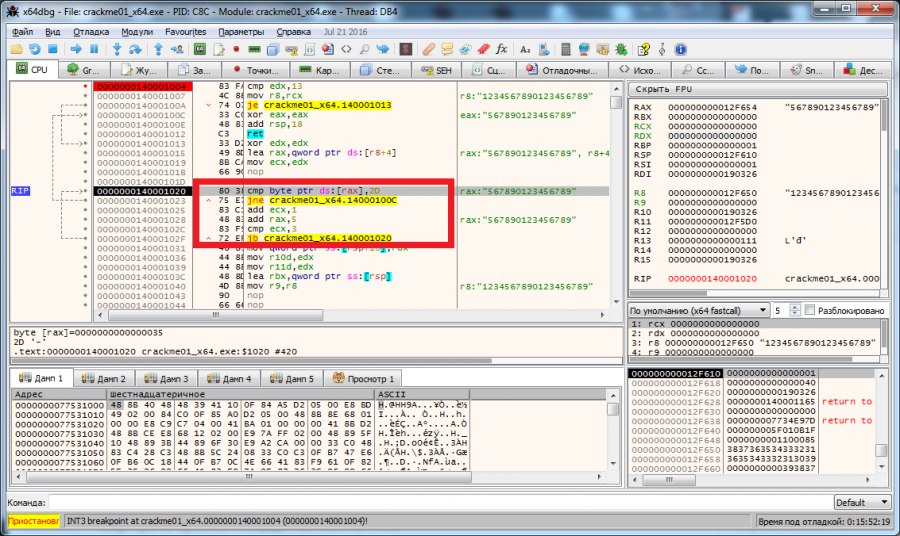
На этом шаге осуществляется проверка каждого пятого символа ключа на равенство значению 2Dh. Дело в том, что число 2Dh — это шестнадцатиричный код символа »-». Т.е. наш ключ должен иметь вид xxxx-xxxx-xxxx-xxxx. Используем в качестве ключа 1234–5678–9012–3456 и переходим к следующему шагу.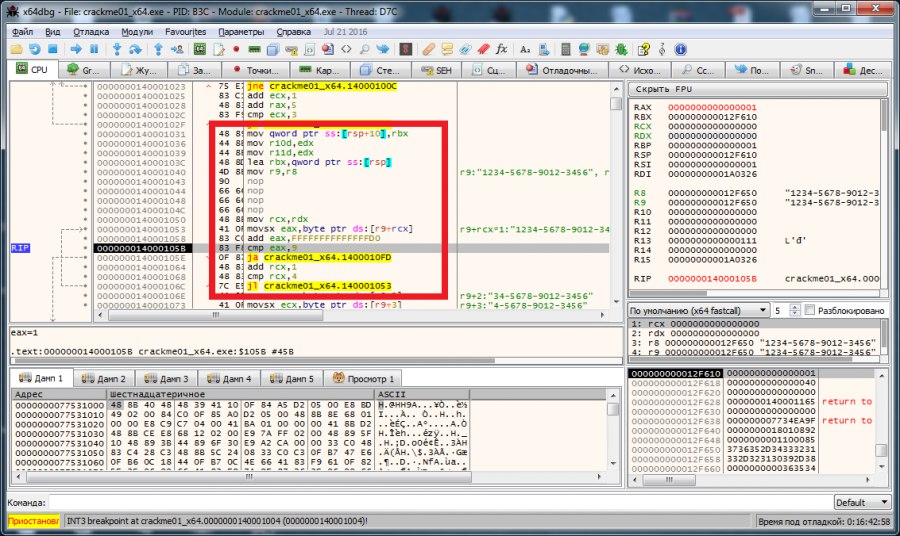
А на следующем шаге происходит проверка символов на числовую принадлежность. Порядок проверки такой: берется символ из ключа (в счет не идут каждый пятый символ ключа) и к его шестнадцатиричному коду прибавляется число -30 и полученный результат сравнивается с числом 9. Если меньше, то на проверку берется следующий символ ключа, если больше, то выводится сообщение, что ключ неверный. Идем дальше.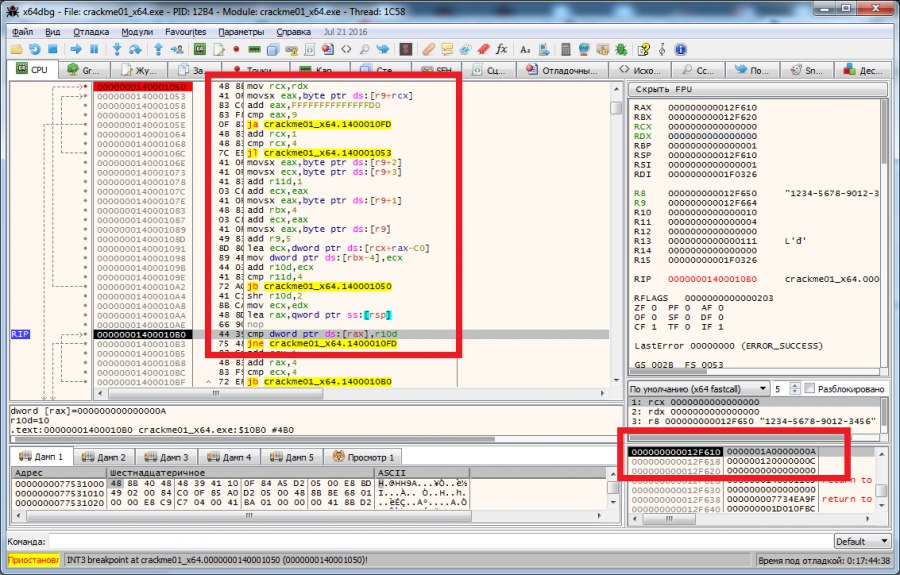
На этом шаге осуществляется проверка того, чтобы суммы чисел в блоках были равны. На рисунке выше выделен блок кода, который производит подсчет суммы чисел и область стека, куда эти суммы заносятся. Параллельно суммы блоков суммируются между собой и заносятся в регистр r10. Далее идет деление результата в регистре r10 на 4 (shr r10d,2 — сдвиг на 2 байта равносилен делению на 4) и сравнение значения из регистра r10 с ранее занесенными значениями в стеке. Отлично. Делаем так, чтобы суммы цифр каждого блока ключа были равны (например 1122–0123–2112–0006) и двигаемся дальше на следующий шаг проверки.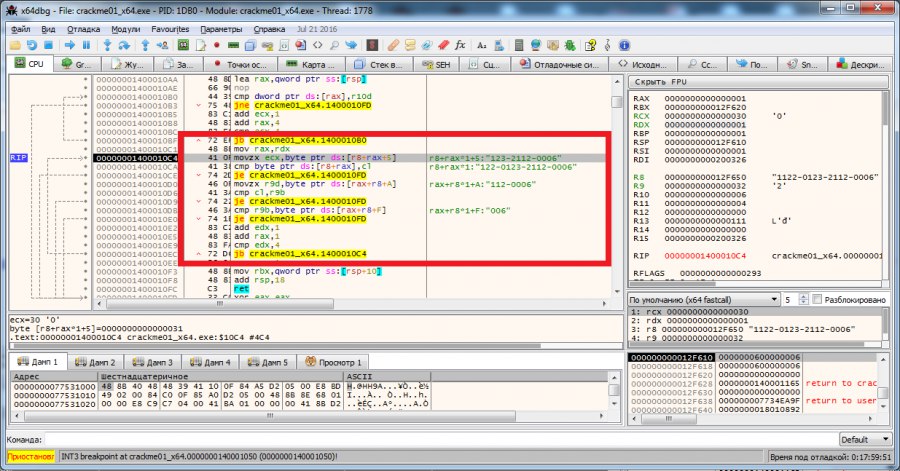
Участок кода, выделенный на рисунке выше, проверяет, чтобы расположение символов в каждом последующем блоке ключа не совпадало с предыдущим. В итоге наш ключ имеет вид 1478–7814–1478–7814. Проверяем.
Отличная работа!

Видим слева в списке функций три функции: start — функция, с которой начинается выполнение программы, DialogFunc — эта функция общается с нами и некоторая функция sub_140001000. Рассмотрим диалоговую функцию. Декомпилируем её Hex Rays-ом.

В глаза бросается ветвление условий, согласно которому, если некоторая функция sub_140001000 вернет TRUE, то появится сообщение, информирующее нас о отлично проделанной работе, иначе неверно. Разберем нашу заветную функцию sub_140001000. Если мы пропустим её через декомпилятор, то увидим, что в качестве аргумента передается указатель всего на одно значение. Вероятно, это значение берется из диалогового окна и является вводимым ключом. Теперь рассмотрим ассемблерный листинг. Имеется первая проверка условия верности введенных данных. Если условие выполняется, то программа исполняется дальше, если не выполняется, то идет возврат из подпрограммы.

Запустим наш crackme под отладчиком. Воспользуемся x64dbg. Поставим breakpoint на нашей первой проверке. В качестве вводимого ключа используем набор цифр 1234567.

Как видно, происходит проверка значения регистра edx и числа 13h (в десятичной системе исчисления это 19). Вероятно, это проверка на количество введенных знаков ключа (у нас их 7 и в регистре edx число 7). Попробуем ввести другое количество символов. Запустим отладчик заново. Введем 9 цифр 123456789.

Похоже, что так оно и есть. Значит наш ключ должен содержать 19 символов. Вводим 19 символов 1234567890123456789 и переходим к следующему этапу проверки.

На этом шаге осуществляется проверка каждого пятого символа ключа на равенство значению 2Dh. Дело в том, что число 2Dh — это шестнадцатиричный код символа »-». Т.е. наш ключ должен иметь вид xxxx-xxxx-xxxx-xxxx. Используем в качестве ключа 1234–5678–9012–3456 и переходим к следующему шагу.

А на следующем шаге происходит проверка символов на числовую принадлежность. Порядок проверки такой: берется символ из ключа (в счет не идут каждый пятый символ ключа) и к его шестнадцатиричному коду прибавляется число -30 и полученный результат сравнивается с числом 9. Если меньше, то на проверку берется следующий символ ключа, если больше, то выводится сообщение, что ключ неверный. Идем дальше.

На этом шаге осуществляется проверка того, чтобы суммы чисел в блоках были равны. На рисунке выше выделен блок кода, который производит подсчет суммы чисел и область стека, куда эти суммы заносятся. Параллельно суммы блоков суммируются между собой и заносятся в регистр r10. Далее идет деление результата в регистре r10 на 4 (shr r10d,2 — сдвиг на 2 байта равносилен делению на 4) и сравнение значения из регистра r10 с ранее занесенными значениями в стеке. Отлично. Делаем так, чтобы суммы цифр каждого блока ключа были равны (например 1122–0123–2112–0006) и двигаемся дальше на следующий шаг проверки.

Участок кода, выделенный на рисунке выше, проверяет, чтобы расположение символов в каждом последующем блоке ключа не совпадало с предыдущим. В итоге наш ключ имеет вид 1478–7814–1478–7814. Проверяем.


Отличная работа!
Комментарии (3)
25 августа 2016 в 19:04
0↑
↓
Круто!
Возможно я покажусь нубом в этом, хотя, так оно и есть, но нельзя ли просто поменять бинарники в местах, где происходит прыжок если условие не выполняется?
Например с je на jne?25 августа 2016 в 19:09
0↑
↓
Это можно, но совершенно некрасиво. Ваш вариант — это «патч» от жадности, вышла новая версия — повторяй заново. Вариант автора — это «кейген», вышла новая версия — ничего не надо делать, если алгоритм ключа не сменили. Плюс вдруг далее где-то проверяется целостность кода, какие-то участки проверки не только проверяют ключ и т.д.25 августа 2016 в 19:15
0↑
↓
Суть в том, что в статье алгоритм проверки ключа был полностью разбран.
А следовательно собеседование пройдет не тот, кто поменял первый je на jmp, а тот, кто смог разобрать все до конца.
