[Из песочницы] Решение квадратных уравнений через производные
Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
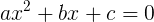
Представим искомое уравнение как функцию:
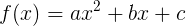
Где, очевидно, необходимо найти такие значения аргумента 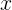 функции, в которых оная возвратила бы ноль.
функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант. Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную! 
Исходя из определения производной ясно, что подставляя аргумент 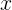 в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.
в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.
Что же дальше делать? Непонятно. А в любом непонятном случае нужно брать производную ещё раз:

На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси  при искомом движении:
при искомом движении:
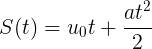
Где  — время,
— время, 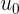 — начальная скорость,
— начальная скорость, 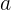 — ускорение.
— ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД. Также нельзя оставлять без внимания тот факт, что формула для РУД выше по факту есть результат взятия интеграла от формулы скорости такого движения. Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» 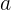 у нас уже есть — им является производная второго порядка
у нас уже есть — им является производная второго порядка 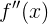 , выведенная выше. А вот чтобы получить начальную скорость
, выведенная выше. А вот чтобы получить начальную скорость 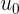 , нам нужно взять в общем-то любой
, нам нужно взять в общем-то любой 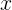 (обозначим его как
(обозначим его как 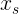 ) и подставить его в производную теперь уже первого порядка
) и подставить его в производную теперь уже первого порядка  — ибо она и будет искомым.
— ибо она и будет искомым.
В таком случае возникает вопрос, какой же 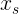 нужно взять? Очевидно, такой, чтобы начальная скорость
нужно взять? Очевидно, такой, чтобы начальная скорость 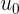 была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:

В таком случае составим уравнение для поиска 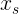 :
:
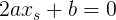 [подставили
[подставили 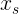 в производную первого порядка
в производную первого порядка  ]
]
Корнем такого уравнения относительно 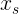 будет:
будет:

А значением исходной функции  при таком аргументе будет:
при таком аргументе будет:

Вспомним, какой целью мы задались в самом начале: «необходимо найти такие значения аргумента 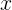 функции, в которых оная возвратила бы ноль». Иными словами, нам от положения
функции, в которых оная возвратила бы ноль». Иными словами, нам от положения  необходимо «дойти до нуля».
необходимо «дойти до нуля».
Так как теперь нам известна начальная скорость, ускорение и какой путь необходимо пройти, то настало время отметить следующее:
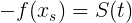 , также как и
, также как и 
Тогда, подставив все известные величины, получим:
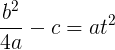
Поделим все на 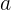 :
:

Теперь становится очевидно, что:

Соединим все «детали пазла» воедино:
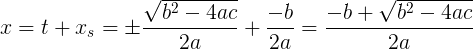
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
