[Из песочницы] Реализация скелетной анимации для трёхмерных моделей10.05.2020 09:07

Здравствуйте! В данный момент на Хабре существует большое количество статей, посвящённых компьютерной графике и реализации различных эффектов, однако текстов на тему реализации скелетной анимации (особенно «с нуля») достаточно немного. Постараюсь восполнить этот пробел с помощью данного текста с описанием технологии и примером несложной реализации на C++ и OpenGL 4.5 (SDL2).

Введение

Перед переходом непосредственно к реализации рассмотрим общие сведения о скелетной анимации и процесс её создания с точки зрения дизайнера. Предполагается, что читатель знаком с принципами работы графических конвейеров, а также с основными терминами и объектами из линейной алгебры (в противном случае можно для начала прочитать следующую статью на данную тему).

При создании компьютерных игр, анимационных фильмов, различных визуализаций повсеместно возникает необходимость использования анимации в том или ином виде. Всевозможные движения персонажей и различные деформации объектов при воздействиях отлично оживляют атмосферу сцены и способствуют погружению игрока или зрителя.

В настоящее время существуют различные технологии реализации анимации, и одной из самых распространённых является анимация скелетная.

Данный вид анимации является улучшенным вариантом более простого метода, который активно применялся в старых играх. Объект, который нужно анимировать, моделировался в виде иерархии (дерева) частей, и для каждой части задавались положения в пространстве в различные моменты времени относительно родительских частей. После этого можно было получить положение любой части объекта в пространстве сцены путём последовательного применения координатных преобразований от дочерних узлов к родительским.

Иерархия частей в таком случае могла выглядеть, например, так:

-  Объект
  - Корпус
      - Левая рука
      - Правая рука
  - Левая нога
  - Правая нога

В таком случае, например, при смещении корпуса в сторону за ним автоматически следовали бы руки из-за того, что их позиции и ориентации были заданы относительно.

Скелетная анимация строится на основе того же иерархического подхода к представлению объектов, но является более гибкой и удобной при использовании с современными видеокартами, обрабатывающими вершины и треугольники.

Подготовка модели на этапе дизайна

Рассмотрим обзорно процесс подготовки модели к анимации на этапе дизайна.

Наиболее часто трёхмерные модели представляются в памяти как набор вершин, образующих примитивы (обычно треугольники). Каждой вершине сопоставляется набор атрибутов, таких как позиция, нормаль, текстурные координаты. Подобный набор вершин позволяет рисовать статические модели.

Для того, чтобы сделать такую модель анимированной, сначала необходимо её подготовить. На первом этапе создаётся так называемый »скелет», то есть набор виртуальных »костей», образующих дерево и отражающих структуру модели. Процесс создания скелета называется риггингом.

На изображении ниже продемонстрирована структура и визуализация скелета трёхмерной модели человека (взята отсюда) при редактировании в Autodesk 3ds Max. Хотя на данной визуализации кости имеют объём, на самом деле они являются точками с привязанными системами координат, что будет более подробно описано ниже.

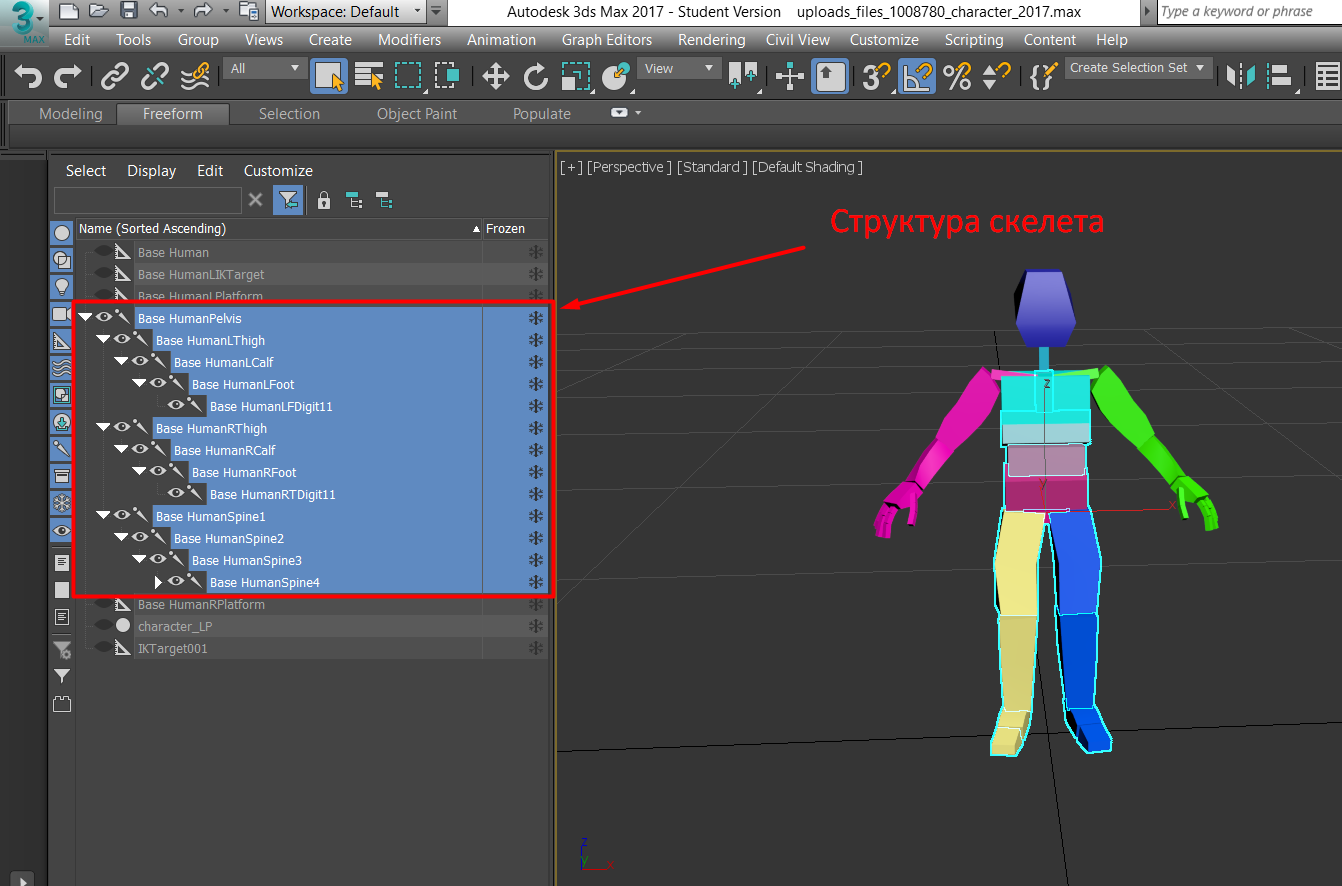
Как можно заметить, каждая кость скелета имеет родительскую кость. Корневая кость является исключением. Родительским объектом для неё является локальная система координат модели. Стоит заметить, что в общем случае 3D-редакторы позволяют размещать несколько моделей на сцене, но здесь системы координат сцены и модели совпадают.

На следующем этапе выполняется привязка вершин модели к созданному скелету (этот процесс называется скиннингом). Каждая вершина может быть привязана к любому количеству костей одновременно (но часто используют не более четырёх костей). В случае привязки к одной вершине нескольких костей, для каждой из них задаётся вес (обычно число от 0.0 до 1.0), определяющий степень влияния кости на данную вершину. Чем больше вес, тем активнее вершина перемещается при движении кости. Сумма весов всех костей для каждой вершины должна равняться единице.

На следующем изображении визуализировано влияние кости на связанные с ней вершины (более тёплые цвета обозначают высокую степень влияния — число более близкое к единице).

Здесь стоит обратить внимание на позу, в которой скелет привязывается к модели (персонаж находится в стоящей позе, руки вытянуты в стороны). Данная поза называется T-позой (так как напоминает букву T) или bind-позой и обычно используется дизайнерами при скиннинге в силу удобства при назначении весов и дальнейшем анимировании.

Анимация модели на этапе дизайна

Анимация (анимационный клип) представляет собой набор кадров, в которых сохраняется информация о положениях костей в соответствующие моменты времени. Атрибутами анимационного клипа являются его длина (количество кадров) и частота (количество кадров в единицу времени, например, секунду).

Так как скелеты могут состоять из большого количества костей, а клипы — из большого количества кадров, сохранять позиции всех костей для каждого кадра было бы слишком затратно, поэтому на самом деле обычно выбирают некоторое количество кадров, в которых и задают положение модели. Такие кадры называются ключевыми. При проигрывании анимации между двумя ключевыми кадрами происходит их интерполяция, в результате которой получается некоторое промежуточное положение.

При перемещении, повороте, масштабировании кости меняют положение все привязанные к ней вершины в соответствии с назначенными весами, а также все дочерние кости.

Когда анимационный клип готов, его можно экспортировать вместе с геометрией модели в одном из форматов, поддерживающих скелетную анимацию, например FBX или COLLADA. Рассмотрение данных форматов не относится напрямую к данной статье. Для работы с данными форматами (и многими другими) можно использовать библиотеку assimp.

Позиционирование модели

Прежде чем рассмотреть проигрывание анимации во времени, необходимо решить задачу о позиционировании модели с помощью скелета, которую можно сформулировать так: для каждой вершины, зная её положение в bind-позе (в ней модель была создана и связана с скелетом), а также имея положения костей в целевой поле, получить положение вершины в целевой позе в требуемый момент времени. Для решения данной задачи придётся обратиться к линейной алгебре.

С точки зрения математики кость представляет собой систему координат, заданную относительно системы координат родительской кости или модели для корневой кости. Для задания кости можно использовать матрицу или SRT-структуру (scale, rotation, translation — масштаб, поворот, перенос/позиция). Масштабирование на практике применяется к костям не очень часто, поэтому в дальнейшем будем считать, что для костей задаются только поворот и позиция относительно родителя, и будем хранить RT-структуру (без R-компонента). Для представления поворота будем использовать кватернионы.

Исходя из этого, на самом деле не очень правильно использовать в данном контексте слово «кость», так как здесь она представляет собой всего лишь материальную точку. Более правильным было бы использовать слово Joint (сустав, соединение), однако со временем данные понятия стали практически взаимозаменяемыми.

Предположим, что к вершине привязана только одна кость. В таком случае для решения поставленной задачи можно сначала перевести координаты вершины в пространство кости, а потом последовательно выполнить переходы между системами координат позиционированных дизайнером костей к корневой кости и обратно в пространство модели. Такая цепочка и даст искомый результат. Рассмотрим её более подробно.

Обозначим матрицу перехода из системы координат кости в систему координат её родителя как $inline$P_{i \to j}$inline$, где $inline$i$inline$ — индекс кости, а $inline$j$inline$ — индекс её родительской кости. Для родителя корневой кости будем использовать индекс $inline$M$inline$, символизирующий локальную систему координат модели в целом. Данную матрицу можно получить из RT-структуры как комбинацию матриц поворота и перемещения.

Другой важной характеристикой кости будет являться матрица перехода из пространства модели в систему координат кости в bind-позе (inverse bind pose matrix). Обозначим её за $inline$ B_{i} $inline$. Данная матрица создаётся на этапе привязки скелета и больше не изменяется.

Позицию вершины в bind-позе (xyz-вектор) обозначим за $inline$ v $inline$, а искомую позицию в анимированной позе — $inline$ v^{'} $inline$.

Рассмотрим на примере следующего скелета:

Пусть мы имеем вершину, привязанную к кости 3 и хотим её позиционировать в соответствии с положением костей. Последовательность преобразований будет выглядеть так:

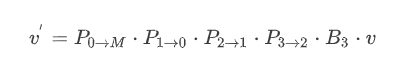
Другими словами, сначача мы переводим координаты вершины в систему координат кости 3 в bind-позе с помощью матрицы $inline$ B_3 $inline$, а затем последовательно применяем матрицы преобразований костей, следуя к корню скелета.

Так как на данном этапе система координат корневой кости не совпадает с системой координат модели, также требуется преобразование $inline$ P_{0 \to M} $inline$.

Можно заметить, что обратная матрица bind-позы является постоянной для кости, а матрицы перехода $inline$P_{i \to j}$inline$ будут определяться временем клипа, но являются общими для всех привязанных к кости вершин.

Для уменьшения количества матричных умножений в этом случае удобно сгенерировать так называемую матричную палитру (matrix palette), в которой для каждой кости хранится предварительно посчитанное произведение матриц bind-позы и матриц перехода. Данное произведение также представляет собой матрицу и позволяет для заданной вершины за одно умножение выполнить переход из bind-позы в анимированную позу.

При использовании современных видеокарт перевод вершинных координат в пространство проекции выполняется в вершинном шейдере, и умножение на матрицу кости из палитры будет выполняться там же. Для этого придётся передавать в шейдер помимо прочих параметров также матричную палитру.

В случае, когда к вершине привязано несколько костей одновременно, позицию в целевой позе можно получить как среднее взвешенное целевых позиций, рассчитанных для каждой позы отдельно.

Проигрывание анимации

Теперь, когда задача о позиционировании модели с помощью скелета решена, проигрывание анимации не должно составить труда. В произвольный момент времени $inline$ t $inline$ для каждой из костей можно найти два соседних ключевых кадра (предыдущий и следующий) и получить текущую позицию путём интерполяции значений в них. Для координат часто применяется линейная интерполяция, а для ориентации, если она задана кватернионом, — сферическая линейная (позволяет избежать резких поворотов и неестественных углов).

Реализация

Итак, настало время переходить к непосредственной реализации. Рассмотрим структуры данных, которые можно использовать для хранения анимированной модели и для проигрывания анимации.

Для работы с векторами, матрицами, кватернионами и другими математическими объектами будем использовать библиотеку glm.

Начнём с костей. Для их хранения создадим следующую структуру:

struct Bone {
  uint8_t parentId; // ID родительской кости (для корневой кости будем зарезервируем идентификатор ROOT_BONE_PARENT_ID, таким образом, скелет сможет содержать не более, чем 254 кости)
  glm::mat4 inverseBindPoseMatrix; // обратная bind-pose матрица для перехода в систему координат кости из пространства модели

  static constexpr uint8_t ROOT_BONE_PARENT_ID = 255; // ID корневой кости
};

Примечание: здесь и в дальнейшем для упрощения кода будем опускать get/set методы, конструкторы, деструкторы, операторы присваивания и подобные элементы структур и классов и будем рассматривать только конкретную часть кода, относящуюся к поставленной задаче. Также оставим реализации необходимых методов в заголовочных файлах.

Скелет будет представлять собой обычный массив костей (удобно будет заполнять этот массив так, чтобы дочерние кости находились в нём после родительских):

struct Skeleton {
  std::vector bones; // массив костей скелета
};

Хранить ключевые кадры будем для каждой кости отдельно. Более того, будем хранить отдельные массивы для ключевых кадров позиций и ориентаций. По сравнению с прямым подходом, когда ключевой кадр представляет собой список позиций и ориентаций всех костей, данный способ позволит существенно выиграть в используемой памяти за счёт удаления избыточных данных.

// Ключевой кадр с позицией кости
struct BoneAnimationPositionFrame {
  float time; // номер кадра
  glm::vec3 position; // позиция относительно родительской кости
};

// Ключевой кадр с ориентацией кости
struct BoneAnimationOrientationFrame {
  float time; // номер кадра
  glm::quat orientation; // ориентация относительно родительской кости
};

Номер кадра в данных структурах на самом деле по своему смыслу — целое число, но для использования в дальнейших расчётах будем хранить его как float.

// Набор ключевых кадров отдельной кости
struct BoneAnimationChannel {
  std::vector positionFrames;
  std::vector orientationFrames;
};

Используя данные структуры, можно загружать и хранить в памяти скелеты и клипы для них. Перейдём непосредственно к анимации. Определим структуры для хранения текущей позы отдельных костей и скелета в целом.

// Поза отдельной кости в заданный момент времени ()
struct BonePose {
  [[nodiscard]] glm::mat4 getBoneMatrix() const
  {
    return glm::translate(glm::identity(), position) * glm::mat4_cast(orientation);
  }

  glm::vec3 position = glm::vec3(0.0f);
  glm::quat orientation = glm::identity();
};

Метод getBoneMatrix() предназначен для получения матрицы перехода из пространства дочерней кости в пространство родительской, то есть той самой матрицы $inline$P_{i \to j}$inline$. Данная матрица является комбинацией перемещения и поворота, заданного кватернионом, причём поворот выполняется первым, так как ассоциативность операций правая. Позицию вершины мы также будем умножать на матрицу справа.

inline BonePose operator*(const BonePose& a, const BonePose& b)
{
  BonePose result;
  result.orientation = a.orientation * b.orientation;
  result.position = a.position + glm::vec3(a.orientation * glm::vec4(b.position, 1.0f));

  return result;
}

Определим структуру матричной палитры:

struct AnimationMatrixPalette {
  std::vector bonesTransforms;
};

Теперь создадим класс, представляющий позу скелета в заданный момент времени, и хранящий локальные позы всех костей (позы, заданные относительно родителей). Именно этот класс будет отвечать за генерацию матричной палитры. При реализации будем предполагать, что позы костей хранятся так, что поза родительской кости хранится перед позой дочерней кости. Это позволит сократить количество умножений и обойтись единственным циклом.

// Поза скелета в отдельный момент времени
class AnimationPose {
 public:
  // Получение матричной палитры для позы
  [[nodiscard]] const AnimationMatrixPalette& getMatrixPalette() const {
    // У корневой кости нет родительской матрицы, поэтому заносим в матричную палитру матрицу перехода как есть
    m_matrixPalette.bonesTransforms[0] = bonesLocalPoses[0].getBoneMatrix();

    auto bonesCount = static_cast(m_matrixPalette.bonesTransforms.size());

    // Пользуясь порядком хранения, проходим по всем локальным позам и выполняем умножения на родительские матрицы
    for (uint8_t boneIndex = 1; boneIndex < bonesCount; boneIndex++) {
      m_matrixPalette.bonesTransforms[boneIndex] =
        m_matrixPalette.bonesTransforms[m_skeleton.bones[boneIndex].parentId] *
          bonesLocalPoses[boneIndex].getBoneMatrix();
    }

    // Умножаем текущее содержимое матричной палитры справа на обратную матрицу bind-позы
    for (uint8_t boneIndex = 0; boneIndex < bonesCount; boneIndex++) {
      m_matrixPalette.bonesTransforms[boneIndex] *= m_skeleton.bones[boneIndex].inverseBindPoseMatrix;
    }

    return m_matrixPalette;
  }

 public:
  std::vector bonesLocalPoses;

 private:
  Skeleton m_skeleton;
  mutable AnimationMatrixPalette m_matrixPalette;
};

Теперь можно переводить модели в произвольные позы с помощью скелета. Осталось реализовать механизм проигрывания анимации во времени и связать данный механизм с отрисовкой модели.

Реализуем класс, представляющий отдельный анимационный клип (например, бег, прицеливание, ходьбу). Начнём с полей.

class AnimationClip {
 // ...
 private:
  Skeleton m_skeleton // скелет, для которого создан данный клип;
  std::vector m_bonesAnimationChannels // списки ключевых кадров для каждой кости скелета;

  mutable AnimationPose m_currentPose; // текущая поза скелета

  float m_currentTime = 0.0f; // счётчик времени (кадры)
  float m_duration = 0.0f; // длительность анимации (кадры)
  float m_rate = 0.0f; // частота анимации (кадры в секунду)

Далее, реализуем простой метода, который увеличивает счётчик прошедшего с начала анимации времени:

  void increaseCurrentTime(float delta) {
    m_currentTime += delta * m_rate;

    if (m_currentTime > m_duration) {
      int overflowParts = static_cast(m_currentTime / m_duration);
      m_currentTime -= m_duration * static_cast(overflowParts);
    }
  }

Данный метод имеет единственный параметр — приращение времени. Внутри происходит увеличение значения счётчика прошедших с начала анимации кадров (получить вещественный номер кадра в данном случае — нормальное явление).

Если оказалось так, что значение счётчика после приращения превысило длительность анимации, отбрасываем переполнение и таким образом зацикливаем анимацию. В общем случае здесь можно было бы действовать по-разному в зависимости от параметров клипа, например, останавливать воспроизведение или автоматически переходить к следующему клипу.

Пересчитывать позу будем при обращении к ней. Так как реализация построения матричной палитры из локальных поз костей уже реализована, нужно добавить лишь инициализацию объекта AnimationPose правильными локальными позами в зависимости от текущего времени. Напишем метод для получения текущей позы скелета.

  [[nodiscard]] const AnimationPose& getCurrentPose() const {
    m_currentPose.bonesLocalPoses[0] = getBoneLocalPose(0, m_currentTime);

    auto bonesCount = static_cast(m_skeleton.bones.size());

    for (uint8_t boneIndex = 1; boneIndex < bonesCount; boneIndex++) {
      m_currentPose.bonesLocalPoses[boneIndex] = getBoneLocalPose(boneIndex, m_currentTime);
    }

    return m_currentPose;
  }

Данный метод просто инициализирует локальные позы костей, получая их с помощью метода getBoneLocalPose(), принимающего индекс кости и текущее время.

  [[nodiscard]] BonePose getBoneLocalPose(uint8_t boneIndex, float time) const
  {
    const std::vector& positionFrames =
      m_bonesAnimationChannels[boneIndex].positionFrames;

    // получаем "среднее" значение позиции кости в текущий момент времени
    auto position = getMixedAdjacentFrames(positionFrames, time);

    const std::vector& orientationFrames =
      m_bonesAnimationChannels[boneIndex].orientationFrames;

    // получаем "среднее" значение ориентации кости в текущий момент времени
    auto orientation = getMixedAdjacentFrames(orientationFrames, time);

    return BonePose(position, orientation);
  }

Так как текущий кадр не обязательно будет являться ключевым, а клип может проигрываться в том числе при дробных номерах текущего кадра, реализуем шаблонный метод getMixedAdjacentFrames, который будет получать «среднее» значение позиции или ориентации в переданный момент времени.

Здесь может встретиться несколько различных ситуаций, которые нужно обработать. Например:

• Текущий кадр является ключевым. Просто используем значение в нём.
• Текущий кадр находится между двумя ключевыми кадрами. Интерполируем значения в них в соответствии с тем, к какому кадров находимся ближе. Если мы находимся в положении $inline$t$inline$, а соседние кадры в положениях $inline$t_0$inline$ и $inline$t_1$inline$ соответственно, то коэффициент интерполяции можно расчитать по формуле $inline$ k = \frac{t — t_0}{t_1 — t_0} $inline$.
• Ключевого кадра справа или слева от текущего не существует. Здесь нет однозначного способа разрешения проблемы. В таком случае можем, например, вернуть значение из ближайшего существующего кадра или принять недостающий кадр за отсутствие преобразований (нулевой вектор позиции, единичный кватернион);

Используя предположение о том, что ключевые кадры хранятся в порядке увеличения времени, для поиска соседних кадров можем использовать бинарный поиск.

  // получает "среднее" значение позиции или ориентации в зависимости от шаблонных параметров
  template
  [[nodiscard]] T getMixedAdjacentFrames(const std::vector& frames, float time) const
  {
    S tempFrame;
    tempFrame.time = time;

    // ищем ближайший следующий кадр
    auto frameIt = std::upper_bound(frames.begin(), frames.end(),
      tempFrame, [](const S& a, const S& b) {
        return a.time < b.time;
      });

    if (frameIt == frames.end()) {
      // если следующего кадра не существует, используем значение последнего
      return (frames.size() > 0) ? getKeyframeValue(*frames.rbegin()) : getIdentity();
    }
    else {
      T next = getKeyframeValue(*frameIt);

      // ищем ближайший предыдущий кадр, а если его не существует, то используем пустой кадр без транформаций
      T prev = (frameIt == frames.begin()) ? getIdentity() : getKeyframeValue(*std::prev(frameIt));

      // интерполируем и возвращаем значение
      float currentFrameTime = frameIt->time;
      float prevFrameTime = (frameIt == frames.begin()) ? 0 : std::prev(frameIt)->time;

      float framesTimeDelta = currentFrameTime - prevFrameTime;

      return getInterpolatedValue(prev, next, (time - prevFrameTime) / framesTimeDelta);
    }
  }

template<>
glm::vec3 AnimationClip::getIdentity() const
{
  return glm::vec3(0.0f);
}

template<>
glm::quat AnimationClip::getIdentity() const
{
  return glm::identity();
}

template<>
glm::vec3 AnimationClip::getKeyframeValue(const BoneAnimationPositionFrame& frame) const
{
  return frame.position;
}

template<>
glm::quat AnimationClip::getKeyframeValue(const BoneAnimationOrientationFrame& frame) const
{
  return frame.orientation;
}

template<>
glm::vec3 AnimationClip::getInterpolatedValue(const glm::vec3& first, const glm::vec3& second, float delta) const
{
  return glm::mix(first, second, delta);
}

template<>
glm::quat AnimationClip::getInterpolatedValue(const glm::quat& first, const glm::quat& second, float delta) const
{
  return glm::slerp(first, second, delta);
}

struct VertexPos3Norm3UVSkinned {
  glm::vec3 pos = {0.0f, 0.0f, 0.0f};
  glm::vec3 norm = {0.0f, 0.0f, 0.0f};
  glm::vec2 uv = {0.0f, 0.0f};
  glm::u8vec4 bonesIds = {0, 0, 0, 0};
  glm::u8vec4 bonesWeights = {0, 0, 0, 0};
};

#version 450 core

layout (location = 0) in vec3 attrPos;
layout (location = 1) in vec3 attrNorm;
layout (location = 2) in vec2 attrUV;
// добавим новые вершинные атрибуты
layout (location = 4) in uvec4 attrBonesIds;
layout (location = 5) in uvec4 attrBonesWeights;

// ...

// добавим структуру для хранения матричной палитры размеров до 128 костей
struct AnimationPalette {
    mat4 palette[128];
};

uniform AnimationPalette animation;

// ...

void main() {
    vec4 position = vec4(attrPos, 1.0);

    // рассчитаем новую позицию с учётом анимации как среднее взвешенное для отдельных костей
    vec4 newPosition = (float(attrBonesWeights[0]) / 255.0) * animation.palette[attrBonesIds[0]] * position + 
(float(attrBonesWeights[1]) / 255.0) * animation.palette[attrBonesIds[1]] * position +
                (float(attrBonesWeights[2]) / 255.0) * animation.palette[attrBonesIds[2]] * position +
                (float(attrBonesWeights[3]) / 255.0) * animation.palette[attrBonesIds[3]] * position;

    outVertexData.uv = attrUV;
    gl_Position = scene.cameraToProjection * scene.worldToCamera * transform.localToWorld * (vec4(newPosition.xyz, 1.0));
}

static void updateScene(float delta)
{
  g_animationClip->increaseCurrentTime(delta);
}

static void renderScene()
{
  // ...

  const AnimationMatrixPalette& currentMatrixPalette = g_animationClip->getCurrentPose().getMatrixPalette();

  setShaderArrayParameter(g_vertexShader, "animation.palette[0]", currentMatrixPalette.bonesTransforms);

  // ...
}