[Из песочницы] R*-tree или индексация геопространственных данных
Приветствую вас, хабражители! В этом посте пойдет речь о геопростарнственной индексации, а именно о такой структуре данных как R*-tree и о том, как я реализовал свой первый проект.Итак, приступим. Сразу же после окончания университета мне поступило предложение от преподавателей, держащих контору, предоставляющую услуги GPS-мониторинга автомобилей, которое я и принял. Вот оно! Наконец-то настоящие интересные проекты! Моей радости и энтузиазма не было границ. Первое же задание, которое мне было дано, имело примерно следующую формулировку: Есть десктопное приложение, в котором кроме всяких там отчетов о пробеге, потраченном топливе автомобилей и.т.д., отображаются векторные карты, с отрисовкой положения этих самых автомобилей в реальном времени, треков истории передвижений авто и всякими прочими плюшками. Сейчас это все работает неправильно и неэффективно. Как реализовать правильно никто не знает. Нужно переписать
…В руки мне были даны исходники приложения на 160 000 строк и все. Никакой документации, ничего. Единственным источником информации были эти самые преподаватели и редкие комментарии в исходниках плана «Убрал н*х по просьбе Васи». Проекту более 10 лет, контора очень лояльно и гибко подходит к просьбам заказчиков в кратчайшие сроки дорисовывая всякие хотелки и свистелки чуть ли не на коленках, которые не документировались. Чудовищная халатность! Зато такие проекты помогают прокачивать навыки разбора чужого кода.Ну что же, задача была поставлена, материал для работы был. Покопавшись в коде, позадавав вопросы я немного прояснил для себя текущее на тот момент положение вещей: Карты лежат массивом точек и объектов со ссылками на эти точки
Объекты, попавшие в область экрана, определяются полным перебором.
Отображать объект или нет, определялось «на лету», расчетом размера объекта на экране (нет смысла тратить ресурсы системы на отображение дома размером в 1 пиксель)
Отрисовка карт небольшого размера (город, район области) происходила сносно. Что происходило при загрузке карт размером с область\страну, содержащих сотни тысяч векторных объектов, состоящих в сумме из миллионов точек, можете себе представить. Погуглив и прочитав уйму материала по теме, я выделил для себя 2 варианта того, как же «правильно» все сделать: Разбить всю область карты на квадраты фиксированного размера, разбить объекты, попадающие на стыки, каждому объекту присвоить индекс квадрата, отсортировать данные и на ходу вычислять нужные объекты;
Использовать R-дерево.
Немного поразмыслив, я откинул первый вариант т.к. нужно было бы привязываться к определенному количеству уровней масштаба и для каждого строить сетку. Второй же вариант давал преимущество неограниченного масштабирования, да и в целом казался более универсальным. Дабы не изобретать велосипед, решил поискать существующие библиотеки под Delphi, т.к. проект писался именно на нем. Библиотеки так и не были найдены и я принял решение реализовать индексацию собственноручно.Что же из себя представляет R-дерево? Данная структура была предложена Антонином Гуттманом для индексации пространственных данных, является сбалансированным деревом и была разработана на основе эмпирических наблюдений. Дерево разбивает пространство на множество вложенных прямоугольников. Каждый узел дерева имеет минимальное (minCount) и максимальное (maxCount) количество объектов. Для корректной работы алгоритмов построения дерева нужно, что бы 2minCountmaxCount / 2. Каждый объект имеет свой ограничивающий прямоугольник — MBR (minimum bounding rectangle). MBR узла является прямоугольник, описывающий прямоугольники дочерних узлов\объектов.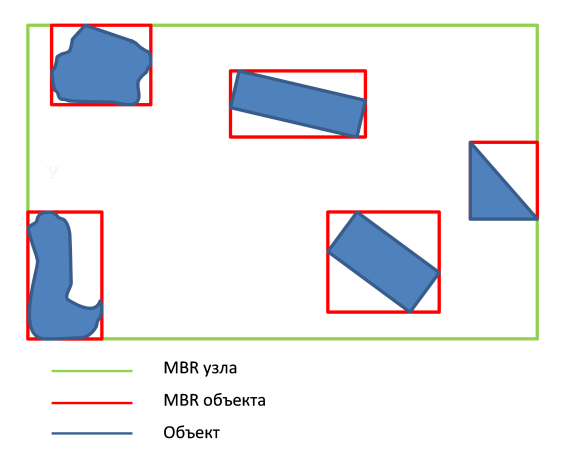
Дерево строится поочередной вставкой в него объектов. При переполнении узла происходит его деление с последующим делением всех родительских узлов при необходимости. Эффективность поисковых запросов для данной структуры данных зависит от нескольких критериев:
Минимизация площади MBR узлов (минимизация пустого пространства между объектами);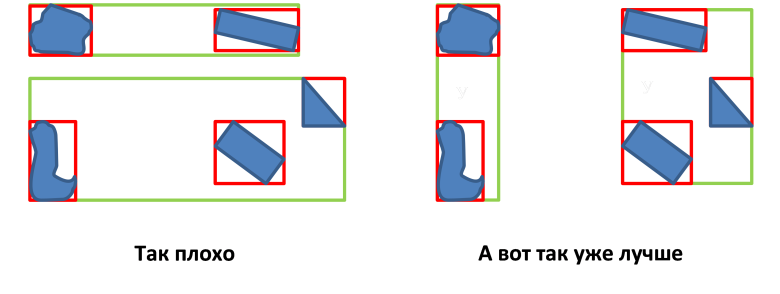 
Минимизация площади перекрытия областей MBR узлов; 
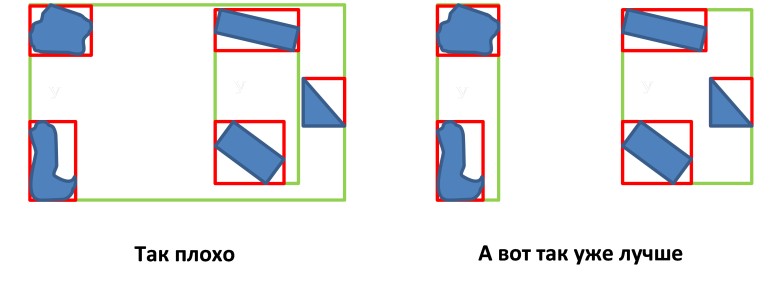Минимизация периметра MBR узла; 
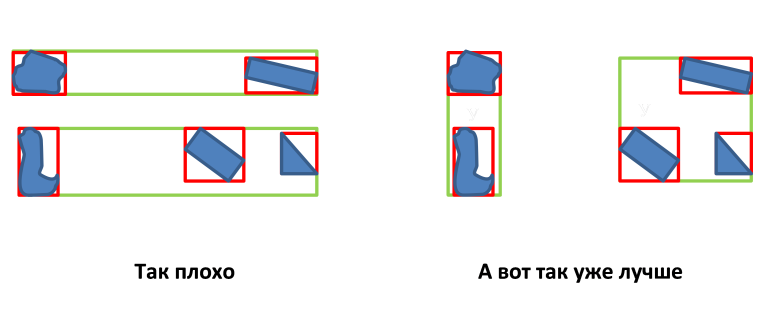Существуют разные типы R-деревьев, различающиеся только способом выбора конечного и деления переполненного узла.Почему я выбрал именно R*-tree? Классический подход, предложенный Антонином Гутманном (R-trees), по моей субъективной оценке совершенно не подходит для использования в реальных проектах. В качестве примера приведу материал из википедии, а именно R-tree, построенное для отделений почты Германии: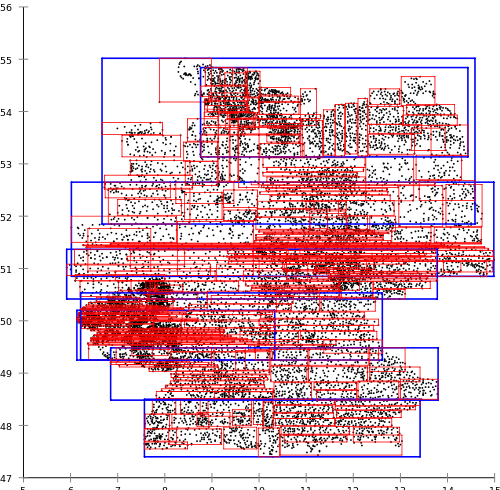 
Когда в то же время алгоритмы R*-дерева, предложенные Норбертом Бекманом (Norbert Beckmann), Ганс-Питер Кригелом (Hans-Peter Kriegel), Ральфом Шнайдером (Ralf Schneider), и Бернардом Зегером (Bernhard Seeger) дают следующий результат: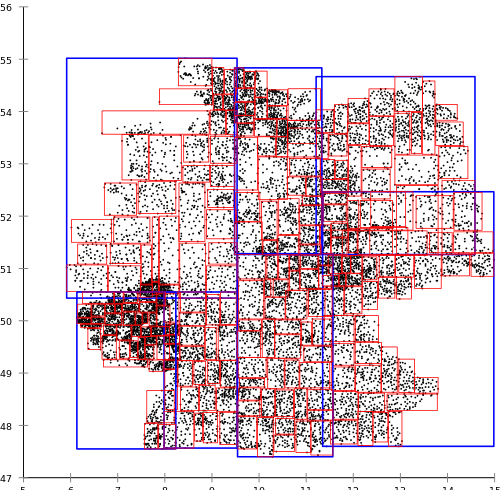 
R*-tree более ресурсоемок при построении, но дает лучшие результаты при поисковых запросах чем обычное R-tree.Рассмотрим, каким же образом происходит вставка: она включает в себя алгоритмы выбора ветки (поддерева)/узла, и алгоритм разделения узла при его переполнении.
Алгоритм выбора поддерева (chooseSubtree) 1.Установить N корневым узлом 2.Если N конечный узел, вернуть N 3.Иначе 4. Если дочерние узлы N являются конечными узлами (листьями), 5. Выбрать дочерний узел N, чей MBR требует наименьшего увеличения перекрытия при вставке объекта в узел 6. Если узлов с наименьшим увеличением перекрытия несколько, выбрать из них тот, который требует наименьшего увеличения площади 7. Если узлов с наименьшим увеличением площади несколько, выбрать из них узел с наименьшей площадью 8. Иначе 9. Выбрать дочерний узел N, чей MBR требует наименьшего увеличения площади 10. Если узлов с наименьшим увеличением площади несколько, выбрать узел с наименьшей площадью 11.Установить N выбранным узлом. 12.Повторить действия начиная с шага 2. Алгоритм деления узла (splitNode) Для нахождения варианта деления, R*- дерево использует следующий метод: узлы сортируются вдоль каждой из осей координат по левой и по правой границах. Для каждого отсортированного варианта узлы делятся на 2 группы таким образом, что для k = [1… (maxCount — 2 * minCount + 2)] в первую группу попадают (minCount — 1) + k узлов, оставшиеся во вторую. Для каждого такого распределения вычисляются следующие показатели: Площадь: Area = Area (MBR первой группы) + Area (MBR второй группы) Периметр: Margin = Margin (MBR первой группы) + Margin (MBR второй группы) Перекрытие: Overlap = Area (MBR первой группы ∩ MBR второй группы) Лучшее распределение определяется следующим алгоритмом: 1. Вызвать chooseSplitAxis для определения оси, по которой будет происходить распределение 2. Вызвать chooseSplitIndex для определения наилучшего распределения по выбранной оси 3. Распределить объекты по 2-м узлам chooseSplitAxis 1. Для каждой из осей 2. Отсортировать узлы по левой, а затем по правой границах их MBR. Распределить узлы как описано выше, вычислить S — сумму всех периметров каждого из распределений. 3. Выбрать ось, с минимальной S. chooseSplitIndex 1. Вдоль выбранной оси выбрать распределение с минимальным параметром перекрытия 2. Если распределений с минимальным параметром перекрытия несколько, выбрать распределение с наименьшей площадью. Собственно сама вставка (insertObject) 1. Вызвать chooseSubStree, передав корневой узел как параметр для определения узла N, в который будет происходить вставка объекта E 2. Если количество объектов в N меньше maxCount, 3. Вставить E в N 4. Обновить MBR для N и всех его родительских узлов 5. Иначе вызвать splitNode для N и E. Авторы R*-дерева в своей статье утверждают, что наилучшая производительность данной структуры достигается при minCount = maxCount * 40%.Вот и все. Наше дерево построено, и теперь найти нужные объекты в заданной области не составляет труда:
Алгоритм поиска объектов в заданной области (findObjectsInArea) 1. Если текущий узел N является конечным, 2. Для каждого дочернего объекта E в узле N, определить, 3. Если E пересекается с областью поиска, добавить E в результат поиска R. 4. Иначе 5. Для каждого дочернего узла n в узле N, определить, 6. Если n пересекается с областью поиска, вызвать для n findObjectsInArea Далее просто вызываем findObjectsInArea, передав ему корневой узел, и область поиска.Для того, что бы более наглядно продемонстрировать работу основных алгоритмов посмотрим на код: Сорцы //построение R*-tree для быстрого поиска геопространсвенных данных unit RStar_tree;
interface
uses Windows, SysUtils, Math;
const MAX_M = 16; // максимальное количество обьектов в узле MIN_M = Round (MAX_M * 0.4); // минимальное количество обьектов в узле
type
TObjArr = array of Integer; // определен для передачи динамического массива в процедуру с последующим изминением размерности этого массива
TAxis = (X, Y); // для chooseSplitAxis — по какой оси будет разделение TBound = (Left, Right); // граница по какой будет идти сортировка (левая\правая)
TGpsPoint = record // структура описывающая точку в системе GPS (X = lon\Y = lat) X, Y: Double; end;
TMBR = record // структура описывающая область покрытия фигуры\узла\итд MBR = Minimum Bounding Rectangle Left, Right: TGpsPoint; // left — координаы верхнего левого угла right — координаты нижнего правого угла end;
TRObject = record // структура описывающая объект в R-дереве. mbr: TMBR; // ограничивающий прямоугольник обьекта idx: Integer; // индекс, ссылка на обьект end;
TRNode = class // узел дерева private fmbr: TMBR; // ограничивающий прямоугольник узла FParent: Integer; // индекс в массиве узлов дерева, указывающий на узел-родитель FChildren: array of Integer; // список индексов дочерних детей в массиве узлов дерева FObjects: array of TRObject; // массив с обьектами. (объект хранит описывающий его прямоугольник и ссылку (индекс) на позициюв массиве фигур (дома, реки, итд) FisLeaf: Boolean; // свойство показывающее является ли этот узел конечным (листом) FLevel: Integer; // уровень узла в дереве (0=лист) protected function getIsLeaf: Boolean; // метод доступа к FisLeaf function getChild (Index: Integer): Integer; // метод доступа дочерним узлам function getObject (Index: Integer): TRObject; // метод доступа к обьектам в узле procedure setChild (Index: Integer; node_id: Integer); // метод присваивания дочернего узла procedure setObject (Index: Integer; obj: TRObject); // метод присваивания обьекта узлу procedure setParent (parent_id: Integer); // метод присваивания узла-родителя Procedure copy (node: TRNode); // метод копирования узла Procedure clearObjects (); // очистить массив обьектов Procedure clearChildren (); // очистит массив дочерних узлов public constructor Create; overload; constructor Create (node: TRNode); overload; destructor Destroy; override; property mbr: TMBR read fmbr write fmbr; // свойство предоставляющее доступ к полям через соответствующие методы property isLeaf: Boolean read FisLeaf; // свойство предоставляющее доступ к полям через соответствующие методы property Children[Index: Integer]: Integer read getChild write setChild; // свойство предоставляющее доступ к полям через соответствующие методы property Objects[Index: Integer]: TRObject read getObject write setObject; // свойство предоставляющее доступ к полям через соответствующие методы property Parent: Integer read FParent write setParent; // свойство предоставляющее доступ к полям через соответствующие методы property Level: Integer read FLevel write FLevel; // свойство предоставляющее доступ к полям через соответствующие методы function isIntersected (mbr1, mbr2: TMBR): Boolean; overload; // метод определяющий пересекаются ли две области mbr1, mbr2 function isIntersected (mbr: TMBR): Boolean; overload; // метод определяющий пересекается ли MBR узла и mbr переданный методу function Overlap (mbr_ovrl: TMBR): Double; // возыращает площадь перекрытия MBR узла и заданной области function Area: Double; overload; // возвращает площадь MBR узла function Area (mbr: TMBR): Double; overload; // возвращает площадь MBR function margin: Double; // возвращает периметр MBR end;
TRtree = class // дерево private FNodeArr: array of TRNode; // массив узлов дерева FRoot: Integer; // ссылка на положение корневого узла в массиве узлов FHeight: Integer; // высота дерева Procedure QuickSort (var List: array of TRObject; iLo, iHi: Integer; axe: TAxis; bound: TBound); overload; // быстрая сортировка для обьектов по их MBR. axe — ось по которой происходит сортировка, bound — граница по которой происходит сортировка (левая/правая) procedure QuickSort (var List: array of Integer; iLo, iHi: Integer; axe: TAxis; bound: TBound); overload; // быстрая сортировка для узлов по их MBR. axe — ось по которой происходит сортировка, bound — граница по которой происходит сортировка (левая/правая) Procedure splitNodeRStar (node_id: Integer; obj: TRObject); overload; // разделяет узел на 2 в соответствии с алгоритмами R*-tree (page 325:: The R*-tree: An Efficient and Robust Access Method for Points and Rectangles+) node_id = ссылка на узел для разделения obj = обьект для вставки Procedure splitNodeRStar (splited_Node_Id, inserted_Node_Id: Integer); overload; // разделяет узел на 2 в соответствии с алгоритмами R*-tree (page 325:: The R*-tree: An Efficient and Robust Access Method for Points and Rectangles+) splited_Node_Id = ссылка на узел для разделения, inserted_Node_Id = узел для вставки Procedure updateMBR (node_id: Integer); overload; // обновляет MBR узла Procedure updateMBR (node: TRNode); overload; // обновляет MBR узла Procedure chooseSubtree (obj: TRObject; var node_id: Integer); // выбор поддерева узла с индексом node_id для вставки обьекта obj. function chooseSplitAxis (obj: TRObject; node_id: Integer): TAxis; overload; // метод выбирающий ось по которой будет происходить деление узла (в соответствии с алгоритмами R*-tree) function chooseSplitAxis (nodeFather, nodeChild: Integer): TAxis; overload; // метод выбирающий ось по которой будет происходить деление узла (в соответствии с алгоритмами R*-tree) Procedure findObjectsInArea (mbr: TMBR; node_id: Integer; var obj: TObjArr); overload; // метод поиска обьектов пересекающихся с областью mbr function isRoot (node_id: Integer): Boolean; // метод определяющий является ли корнем узел с индексом node_id function newNode (): Integer; // метод создания нового узла. Возвращает индекс только что созданого узла protected
public constructor Create; destructor Destroy; override; Procedure insertObject (obj: TRObject); // метод для вставки обьекта в дерево Procedure findObjectsInArea (mbr: TMBR; var obj: TObjArr); overload; // метод для поиска обьектов попадающих в область mbr. Возвращает массив содержащий индексы на фигуры в массиве фигур (обьектов. т.е. домов, рек итд) property Height: Integer read FHeight; // свойство возвращающее высоту дерева end;
function toRObject (lx, ly, rx, ry: Double; idx: Integer): TRObject; overload; function toRObject (mbr: TMBR; idx: Integer): TRObject; overload;
implementation
function toRObject (lx, ly, rx, ry: Double; idx: Integer): TRObject; begin Result.mbr.Left.X:= Min (lx, rx); Result.mbr.Left.Y:= Min (ly, ry); Result.mbr.Right.X:= Max (lx, rx); Result.mbr.Right.Y:= Max (ly, ry); Result.idx:= idx; end;
function toRObject (mbr: TMBR; idx: Integer): TRObject; begin Result.mbr:= mbr; Result.idx:= idx; end; { TRNode }
function TRNode.Area: Double; begin Result:= (fmbr.Right.X — fmbr.Left.X) * (fmbr.Right.Y — fmbr.Left.Y); end;
function TRNode.Area (mbr: TMBR): Double; begin Result:= (mbr.Right.X — mbr.Left.X) * (mbr.Right.Y — mbr.Left.Y); end;
procedure TRNode.clearChildren; begin SetLength (FChildren, 0); end;
procedure TRNode.clearObjects; begin FisLeaf:= False; SetLength (FObjects, 0); end;
procedure TRNode.copy (node: TRNode); var i: Integer; begin SetLength (FObjects, Length (node.FObjects)); SetLength (FChildren, Length (node.FChildren));
if Length (FObjects) > 0 then begin for i:= 0 to High (node.FObjects) do begin FObjects[i].idx:= node.FObjects[i].idx; FObjects[i].mbr.Left.X:= node.FObjects[i].mbr.Left.X; FObjects[i].mbr.Left.Y:= node.FObjects[i].mbr.Left.Y; FObjects[i].mbr.Right.X:= node.FObjects[i].mbr.Right.X; FObjects[i].mbr.Right.Y:= node.FObjects[i].mbr.Right.Y; end; FisLeaf:= True; end else begin for i:= 0 to High (node.FChildren) do begin Children[i] := node.Children[i]; end; FisLeaf:= False; end;
fmbr.Left.X:= node.fmbr.Left.X; fmbr.Left.Y:= node.fmbr.Left.Y; fmbr.Right.X:= node.fmbr.Right.X; fmbr.Right.Y:= node.fmbr.Right.Y;
FParent:= node.Parent; FLevel:= node.Level; end;
constructor TRNode.Create (node: TRNode); begin Create; FParent:= -10; copy (node); end;
constructor TRNode.Create; begin inherited; FParent:= -10; end;
destructor TRNode.Destroy; begin SetLength (FObjects, 0); SetLength (FChildren, 0); inherited; end;
function TRNode.getChild (Index: Integer): Integer; begin if High (FChildren) >= Index then begin Result:= FChildren[Index]; end; end;
function TRNode.getIsLeaf: Boolean; begin if Length (FObjects) > 0 then Result:= True else Result:= False; end;
function TRNode.getObject (Index: Integer): TRObject; begin if High (FObjects) >= Index then begin Result:= FObjects[Index]; end; end;
function TRNode.isIntersected (mbr: TMBR): Boolean; begin Result:= False; if (fmbr.Left.X <= mbr.Right.X) and (fmbr.Left.Y <= mbr.Right.Y) then begin if (fmbr.Right.X >= mbr.Left.X) and (fmbr.Right.Y >= mbr.Left.Y) then begin Result:= True; end; end; end;
function TRNode.margin: Double; begin Result:= ((fmbr.Right.X — fmbr.Left.X) + (fmbr.Right.Y — fmbr.Left.Y)) * 2; end;
function TRNode.Overlap (mbr_ovrl: TMBR): Double; var X, Y: Double; begin X:= Min (mbr_ovrl.Right.X, fmbr.Right.X) — Max (mbr_ovrl.Left.X, fmbr.Left.X); if X <= 0 then begin Result := 0; Exit; end; Y := Min(mbr_ovrl.Right.Y, fmbr.Right.Y) - Max(mbr_ovrl.Left.Y, fmbr.Left.Y); if Y <= 0 then begin Result := 0; Exit; end; Result := X * Y; end;
function TRNode.isIntersected (mbr1, mbr2: TMBR): Boolean; begin Result:= False; if (mbr1.Left.X <= mbr2.Right.X) and (mbr1.Left.Y <= mbr2.Right.Y) then begin if (mbr1.Right.X >= mbr2.Left.X) and (mbr1.Right.Y >= mbr2.Left.Y) then begin Result:= True; end; end; end;
procedure TRNode.setChild (Index, node_id: Integer); begin if High (FChildren) >= Index then begin FChildren[Index] := node_id; FisLeaf:= False; end else begin if ((Index) <= (MAX_M - 1)) and (Index >= 0) then begin SetLength (FChildren, Index + 1); FChildren[Index] := node_id; FisLeaf:= False; end; end; end;
procedure TRNode.setObject (Index: Integer; obj: TRObject); begin if High (FObjects) >= Index then begin FObjects[Index] := obj; FisLeaf:= True; end else begin if ((Index) <= (MAX_M - 1)) and (Index >= 0) then begin SetLength (FObjects, Index + 1); FObjects[Index] := obj; FisLeaf:= True; end; end; end;
procedure TRNode.setParent (parent_id: Integer); begin if parent_id >= 0 then FParent:= parent_id; end;
{ TRtree }
function TRtree.chooseSplitAxis (obj: TRObject; node_id: Integer): TAxis; var arr_obj: array of TRObject; i, j, k, idx: Integer; node_1, node_2: TRNode; perimeter_min, perimeter: Double; begin SetLength (arr_obj, MAX_M + 1);
if not FNodeArr[node_id].isLeaf then Exit;
for i:= 0 to High (FNodeArr[node_id].FObjects) do begin arr_obj[i] := FNodeArr[node_id].FObjects[i]; end;
arr_obj[ High (arr_obj)] := obj;
node_1:= TRNode.Create; node_2:= TRNode.Create;
perimeter_min:= 999999;
for i:= 0 to 1 do // оси begin perimeter:= 0;
for j:= 0 to 1 do // левые и правые углы (границы) begin node_1.clearObjects; node_2.clearObjects;
QuickSort (arr_obj, 0, High (arr_obj), TAxis (i), TBound (j));
for k:= 1 to MAX_M — MIN_M * 2 + 2 do // высчитываем периметры во всех возможных комбинациях begin idx:= 0;
while idx < ((MIN_M - 1) + k) do // первому узлу присваиваются первые (MIN_M - 1) + k элементов begin node_1.Objects[idx] := arr_obj[idx]; idx := idx + 1; end;
for idx:= idx to High (arr_obj) do // второму узлу присваиваем остальные элементы begin node_2.Objects[idx — ((MIN_M — 1) + k)] := arr_obj[idx]; end;
updateMBR (node_1); updateMBR (node_2);
perimeter:= perimeter + ((node_1.mbr.Right.X — node_1.mbr.Left.X) * 2 + (node_1.mbr.Right.Y — node_1.mbr.Left.Y) * 2); end;
end;
if perimeter <= perimeter_min then begin Result := TAxis(i); perimeter_min := perimeter; end;
perimeter:= 0; end;
SetLength (arr_obj, 0); FreeAndNil (node_1); FreeAndNil (node_2); end;
function TRtree.chooseSplitAxis (nodeFather, nodeChild: Integer): TAxis; var arr_node: array of Integer; i, j, k, idx: Integer; node_1, node_2: TRNode; perimeter_min, perimeter: Double; begin SetLength (arr_node, MAX_M + 1);
for i:= 0 to High (FNodeArr[nodeFather].FChildren) do begin arr_node[i] := FNodeArr[nodeFather].FChildren[i]; end;
arr_node[ High (arr_node)] := nodeChild;
perimeter_min:= 999999;
node_1:= TRNode.Create; node_2:= TRNode.Create;
for i:= 0 to 1 do // оси begin perimeter:= 0;
for j:= 0 to 1 do // левые и правые углы (границы) begin node_1.clearChildren; node_2.clearChildren;
QuickSort (arr_node, 0, High (arr_node), TAxis (i), TBound (j));
for k:= 1 to MAX_M — MIN_M * 2 + 2 do // высчитываем периметры во всех возможных комбинациях begin idx:= 0;
while idx < ((MIN_M - 1) + k) do // первому узлу присваиваются первые (MIN_M - 1) + k элементов begin node_1.Children[idx] := arr_node[idx]; idx := idx + 1; end;
for idx:= idx to High (arr_node) do // второму узлу присваиваем остальные элементы begin node_2.Children[idx — ((MIN_M — 1) + k)] := arr_node[idx]; end;
updateMBR (node_1); updateMBR (node_2);
perimeter:= perimeter + node_1.margin + node_2.margin; end;
end;
if perimeter <= perimeter_min then begin Result := TAxis(i); perimeter_min := perimeter; end;
perimeter:= 0; end; FreeAndNil (node_1); FreeAndNil (node_2); SetLength (arr_node, 0); end;
procedure TRtree.chooseSubtree (obj: TRObject; var node_id: Integer); var i, id_child: Integer;
min_overlap_enlargement: Double; // минимальное увеличение перекрытия узла и обьекта Overlap_enlargement: Double; area_enlargement: Double;
idChild_overlap: array of Integer; { массив индексов узлов с минимальным расширением перекрытия. Требуется массив потому, что вставка обьекта может вообще не расширять перекрытие, для этого занесем все индексы в массив и выберем узел с минимальным расширением площади MBR }
idChild_area: array of Integer; { массив индексов узлов с минимальным расширением площади. Требуется массив потому, что вставка обьекта может вообще не расширять площадь MBR узла, для этого занесем все индексы в массив и выберем узел с минимальной площадью MBR }
id_zero: Integer; { перемення для хранения индекса дочернего узла при поиске узла с наименьшей площадью MBR (в случае когда имеется несколько узлов без расширения MBR) }
enlargement_mbr: TMBR; // для расчета ИЗМЕНЕНИЯ MBR dx, dy, dspace: Double; // для расчета УВЕЛИЧЕНИЯ MBR по x, y и площади has_no_enlargement: Boolean; // есть ли область без увеличения begin
if FNodeArr[node_id].isLeaf then // если узел конечный, возвращяем его begin Exit; end;
SetLength (idChild_overlap, 1); SetLength (idChild_area, 1);
dx:= 0; dy:= 0; dspace:= 9999999; id_zero:= 0; has_no_enlargement:= False; min_overlap_enlargement:= 999999;
if FNodeArr[FNodeArr[node_id].Children[0]].isLeaf then // если дочерние узлы являются конечными (листьями) begin { определяем узел с наименьшим увеличением перекрытия } for i:= 0 to High (FNodeArr[node_id].FChildren) do begin
id_child:= FNodeArr[node_id].FChildren[i]; Overlap_enlargement:= FNodeArr[id_child].Area (obj.mbr) — FNodeArr[id_child].Overlap (obj.mbr);
if Overlap_enlargement <= min_overlap_enlargement then begin if Overlap_enlargement = min_overlap_enlargement then // если увеличение перекытия равно предидущему минимальному begin SetLength(idChild_overlap, Length(idChild_overlap) + 1); idChild_overlap[ High(idChild_overlap)] := i; end else // если увеличение перекрытия строго меньше предидущего минимального begin min_overlap_enlargement := Overlap_enlargement; if Length(idChild_overlap) = 1 then // если до этого не встречались два узла с одинаковым минимальным значением idChild_overlap[0] := i else begin SetLength(idChild_overlap, 1); // если же встречались, тогда установим длину массива равной 1 idChild_overlap[0] := i end; end; end; end;
if Length (idChild_overlap) = 1 then // если в массиве всего 1 элемент тогда найден элемент с минимальным расширением перекрытия begin node_id:= FNodeArr[node_id].Children[idChild_overlap[0]]; chooseSubtree (obj, node_id); // рекурсивно вызываем процедуру выбора поддерева Exit; end; end else // если же дочерние узлы не конечные begin SetLength (idChild_overlap, Length (FNodeArr[node_id].FChildren)); for i:= 0 to High (FNodeArr[node_id].FChildren) do // скопируем индексы в массив idChild_overlap, так как дальше процедура работает с этим массивом (на случай если дочерние узлы конечные и имеется несколько узлов с одинаковым увеличением перекрытия, тогда в idChild_overlap будут индексы на эти узлы) idChild_overlap[i] := i; end;
{ определяем узел с наименьшим увеличением площади }
for i:= 0 to High (idChild_overlap) do begin id_child:= FNodeArr[node_id].FChildren[idChild_overlap[i]];
enlargement_mbr.Left.X:= Min (obj.mbr.Left.X, FNodeArr[id_child].mbr.Left.X); enlargement_mbr.Left.Y:= Min (obj.mbr.Left.Y, FNodeArr[id_child].mbr.Left.Y); enlargement_mbr.Right.X:= Max (obj.mbr.Right.X, FNodeArr[id_child].mbr.Right.X); enlargement_mbr.Right.Y:= Max (obj.mbr.Right.Y, FNodeArr[id_child].mbr.Right.Y);
area_enlargement:= FNodeArr[id_child].Area (enlargement_mbr) — FNodeArr[id_child].Area;
if area_enlargement <= dspace then begin if area_enlargement = dspace then // если увеличение площади равно предидущему минимальному begin SetLength(idChild_area, Length(idChild_area) + 1); idChild_area[ High(idChild_area)] := i; end else // если увеличение площади строго меньше предидущего минимального begin dspace := area_enlargement; if Length(idChild_area) = 1 then // если до этого не встречались два узла с одинаковым минимальным значением idChild_area[0] := i else begin SetLength(idChild_area, 1); // если же встречались, тогда установим длину массива равной 1 idChild_area[0] := i end; end; end;
end;
if Length (idChild_area) = 1 then // если в масиве всего один элемент, тогда найден узел с минимальным расширением MBR begin node_id:= FNodeArr[node_id].Children[idChild_area[0]]; chooseSubtree (obj, node_id); // рекурсивно вызываем процедуру выбора поддерева end else // в противном случае (имееться несколько узлов без расширения MBR либо с одинаковым расширением) находим узел с минимальной площадью MBR begin dspace:= 999999;
for i:= 0 to High (idChild_area) do begin id_child:= FNodeArr[node_id].Children[idChild_area[i]];
if FNodeArr[id_child].Area < dspace then begin id_zero := idChild_area[i]; dspace := FNodeArr[id_child].Area; end; end;
node_id:= FNodeArr[node_id].Children[id_zero]; chooseSubtree (obj, node_id); end; end;
constructor TRtree.Create; begin inherited; SetLength (FNodeArr, 1); FNodeArr[0] := TRNode.Create; FRoot:= 0; FNodeArr[FRoot].FisLeaf:= True; end;
destructor TRtree.Destroy; var i: Integer; begin for i:= 0 to High (FNodeArr) do FreeAndNil (FNodeArr[i]); SetLength (FNodeArr, 0); inherited; end;
procedure TRtree.findObjectsInArea (mbr: TMBR; node_id: Integer; var obj: TObjArr); var i: Integer; begin if isRoot (node_id) then SetLength (obj, 0);
if not FNodeArr[node_id].isLeaf then begin for i:= 0 to High (FNodeArr[node_id].FChildren) do begin if FNodeArr[FNodeArr[node_id].Children[i]].isIntersected (mbr) then findObjectsInArea (mbr, FNodeArr[node_id].Children[i], obj); end; end else begin for i:= 0 to High (FNodeArr[node_id].FObjects) do begin if FNodeArr[node_id].isIntersected (mbr, FNodeArr[node_id].Objects[i].mbr) then begin SetLength (obj, Length (obj) + 1); obj[ High (obj)] := FNodeArr[node_id].Objects[i].idx; end; end; end; end;
procedure TRtree.findObjectsInArea (mbr: TMBR; var obj: TObjArr); begin findObjectsInArea (mbr, FRoot, obj); end;
procedure TRtree.insertObject (obj: TRObject); var node_id: Integer; begin node_id:= FRoot; chooseSubtree (obj, node_id);
if Length (FNodeArr[node_id].FObjects) < MAX_M then // если количетсво обьектов в узле меньше максимально допустимого begin FNodeArr[node_id].Objects[ High(FNodeArr[node_id].FObjects) + 1] := obj; updateMBR(node_id); end else // если количество обьектов в узле достигло максимально допустимое begin splitNodeRStar(node_id, obj); // делим узел end;
end;
function TRtree.isRoot (node_id: Integer): Boolean; begin if node_id = FRoot then Result:= True else Result:= False; end;
function TRtree.newNode: Integer; begin SetLength (FNodeArr, Length (FNodeArr) + 1); FNodeArr[ High (FNodeArr)] := TRNode.Create; Result:= High (FNodeArr); end;
procedure TRtree.QuickSort (var List: array of TRObject; iLo, iHi: Integer; axe: TAxis; bound: TBound); var Lo: Integer; Hi: Integer; T: TRObject; Mid: Double; begin Lo:= iLo; Hi:= iHi;
case bound of Left: case axe of X: Mid:= List[(Lo + Hi) div 2].mbr.Left.X; Y: Mid:= List[(Lo + Hi) div 2].mbr.Left.Y; end; Right: case axe of X: Mid:= List[(Lo + Hi) div 2].mbr.Right.X; Y: Mid:= List[(Lo + Hi) div 2].mbr.Right.Y; end; end;
repeat
case bound of Left: case axe of X: begin while List[Lo].mbr.Left.X < Mid do Inc(Lo); while List[Hi].mbr.Left.X > Mid do Dec (Hi); end; Y: begin while List[Lo].mbr.Left.Y < Mid do Inc(Lo); while List[Hi].mbr.Left.Y > Mid do Dec (Hi); end; end; Right: case axe of X: begin while List[Lo].mbr.Right.X < Mid do Inc(Lo); while List[Hi].mbr.Right.X > Mid do Dec (Hi); end; Y: begin while List[Lo].mbr.Right.Y < Mid do Inc(Lo); while List[Hi].mbr.Right.Y > Mid do Dec (Hi); end; end; end;
if Lo <= Hi then begin T := List[Lo]; List[Lo] := List[Hi]; List[Hi] := T; Inc(Lo); Dec(Hi); end;
until Lo > Hi;
if Hi > iLo then QuickSort (List, iLo, Hi, axe, bound); if Lo < iHi then QuickSort(List, Lo, iHi, axe, bound); end;
procedure TRtree.QuickSort (var List: array of Integer; iLo, iHi: Integer; axe: TAxis; bound: TBound); var Lo: Integer; Hi: Integer; T: Integer; Mid: Double; begin Lo:= iLo; Hi:= iHi;
case bound of Left: case axe of X: Mid:= FNodeArr[List[(Lo + Hi) div 2]].mbr.Left.X; Y: Mid:= FNodeArr[List[(Lo + Hi) div 2]].mbr.Left.Y; end; Right: case axe of X: Mid:= FNodeArr[List[(Lo + Hi) div 2]].mbr.Right.X; Y: Mid:= FNodeArr[List[(Lo + Hi) div 2]].mbr.Right.Y; end; end;
repeat
case bound of Left: case axe of X: begin while FNodeArr[List[Lo]].mbr.Left.X < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Left.X > Mid do Dec (Hi); end; Y: begin while FNodeArr[List[Lo]].mbr.Left.Y < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Left.Y > Mid do Dec (Hi); end; end; Right: case axe of X: begin while FNodeArr[List[Lo]].mbr.Right.X < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Right.X > Mid do Dec (Hi); end; Y: begin while FNodeArr[List[Lo]].mbr.Right.Y < Mid do Inc(Lo); while FNodeArr[List[Hi]].mbr.Right.Y > Mid do Dec (Hi); end; end; end;
if Lo <= Hi then begin T := List[Lo]; List[Lo] := List[Hi]; List[Hi] := T; Inc(Lo); Dec(Hi); end;
until Lo > Hi;
if Hi > iLo then QuickSort (List, iLo, Hi, axe, bound); if Lo < iHi then QuickSort(List, Lo, iHi, axe, bound); end;
procedure TRtree.splitNodeRStar (splited_Node_Id, inserted_Node_Id: Integer); var axe: TAxis; parent_id, new_child_id: Integer; node_1, node_2, node_1_min, node_2_min: TRNode; i, j, k: Integer; arr_node: array of Integer; area_overlap_min, area_overlap, // для расчета текущей и минимальной площади перекрытия областей area_min, Area: Double; // для расчета текущей и минимальной площадей областей
begin
if FNodeArr[splited_Node_Id].isLeaf then Exit;
if isRoot (splited_Node_Id) then begin parent_id:= newNode; // создаем новый узел в массиве дерева и получаем его id FNodeArr[FRoot].Parent:= parent_id; // присваиваем этот id корневому узлу, как родитель FNodeArr[parent_id].Children[0] := FRoot; // присваиваем новому узлу id корня как дочерний узел FNodeArr[parent_id].Level:= FNodeArr[FNodeArr[parent_id].Children[0]].Level + 1; // увеличиваем уровень нового узла на 1 FRoot:= parent_id; // изменяем id корня на id нового узла FHeight:= FHeight + 1; // увеличиваем высоту дерева end else begin parent_id:= FNodeArr[splited_Node_Id].Parent; end;
SetLength (arr_node, MAX_M + 1);
for i:= 0 to High (arr_node) — 1 do arr_node[i] := FNodeArr[splited_Node_Id].Children[i];
arr_node[ High (arr_node)] := inserted_Node_Id;
node_1_min:= TRNode.Create; node_2_min:= TRNode.Create;
node_1:= TRNode.Create; node_2:= TRNode.Create;
axe:= chooseSplitAxis (splited_Node_Id, inserted_Node_Id);
area_overlap_min:= 9999999; area_min:= 9999999;
for i:= 0 to 1 do begin QuickSort (arr_node, 0, High (arr_node), axe, TBound (i));
for k:= MIN_M — 1 to MAX_M — MIN_M do begin
node_1.clearChildren; node_2.clearChildren;
j:= 0;
while j <= k do begin node_1.Children[j] := arr_node[j]; j := j + 1; end;
for j:= k to High (arr_node) — 1 do begin node_2.Children[j — k] := arr_node[j + 1]; end;
updateMBR (node_1); updateMBR (node_2);
area_overlap:= node_1.Overlap (node_2.mbr);
if area_overlap < area_overlap_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_overlap_min := area_overlap; end else begin if area_overlap = area_overlap_min then // если площади перекрытия одинаковые begin Area := node_1.Area + node_2.Area; // считаем площади узлов if Area < area_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_min := Area; end; end; end; end;
end;
node_1_min.Level:= FNodeArr[splited_Node_Id].Level; node_2_min.Level:= FNodeArr[splited_Node_Id].Level;
FNodeArr[splited_Node_Id].copy (node_1_min); // вставляем первый узел на место старого (переполненого) узла FNodeArr[splited_Node_Id].Parent:= parent_id;
new_child_id:= newNode; // создаем новый узел в массиве узлов дерева FNodeArr[new_child_id].copy (node_2_min); // вставляем в только что созданный узел второй узел FNodeArr[new_child_id].Parent:= parent_id; // присваиваем id узла родителя значению parent нового узла
FreeAndNil (node_1); FreeAndNil (node_2); FreeAndNil (node_1_min); FreeAndNil (node_2_min);
for i:= 0 to High (FNodeArr[new_child_id].FChildren) do // присваиваем значению Parent всех детей нового узла его id begin FNodeArr[FNodeArr[new_child_id].Children[i]].Parent:= new_child_id end;
if Length (FNodeArr[parent_id].FChildren) < MAX_M then // если хватает места для вставки второго узла begin FNodeArr[parent_id].Children[ High(FNodeArr[parent_id].FChildren) + 1] := new_child_id; // присваиваем id нового узла updateMBR(parent_id); end else // если места не хватает begin splitNodeRStar(parent_id, new_child_id); // вызываем процедуру деления родительского узла end;
end;
procedure TRtree.splitNodeRStar (node_id: Integer; obj: TRObject); var axe: TAxis; parent_id, new_child_id: Integer; node_1, node_2, node_1_min, node_2_min: TRNode; i, j, k: Integer; arr_obj: array of TRObject; area_overlap_min, area_overlap, // для расчета текущей и минимальной площади перекрытия областей area_min, Area: Double; // для расчета текущей и минимальной площадей областей
begin
if not FNodeArr[node_id].isLeaf then Exit;
if isRoot (node_id) then begin parent_id:= newNode; // создаем новый узел в массиве дерева и получаем его id FNodeArr[FRoot].Parent:= parent_id; // присваиваем этот id корневому узлу, как родитель FNodeArr[parent_id].Children[0] := FRoot; // присваиваем новому узлу id корня как дочерний узел FNodeArr[parent_id].Level:= FNodeArr[FNodeArr[parent_id].Children[0]].Level + 1; // увеличиваем уровень нового узла на 1 FRoot:= parent_id; // изменяем id корня на id нового узла FHeight:= FHeight + 1; // увеличиваем высоту дерева end else begin parent_id:= FNodeArr[node_id].Parent; end;
SetLength (arr_obj, MAX_M + 1);
for i:= 0 to High (arr_obj) — 1 do arr_obj[i] := FNodeArr[node_id].Objects[i];
arr_obj[ High (arr_obj)] := obj;
node_1_min:= TRNode.Create; node_2_min:= TRNode.Create;
node_1:= TRNode.Create; node_2:= TRNode.Create;
axe:= chooseSplitAxis (obj, node_id);
area_overlap_min:= 9999999; area_min:= 9999999;
for i:= 0 to 1 do begin QuickSort (arr_obj, 0, High (arr_obj), axe, TBound (i));
for k:= MIN_M — 1 to MAX_M — MIN_M do begin
node_1.clearObjects; node_2.clearObjects;
j:= 0;
while j <= k do begin node_1.Objects[j] := arr_obj[j]; j := j + 1; end;
for j:= k to High (arr_obj) — 1 do begin node_2.Objects[j — k] := arr_obj[j + 1]; end;
updateMBR (node_1); updateMBR (node_2);
area_overlap:= node_1.Overlap (node_2.mbr);
if area_overlap < area_overlap_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_overlap_min := area_overlap; end else begin if area_overlap = area_overlap_min then // если площади перекрытия одинаковые begin Area := node_1.Area + node_2.Area; // считаем площади узлов if Area < area_min then begin node_1_min.copy(node_1); node_2_min.copy(node_2); area_min := Area; end; end; end; end;
end;
node_1_min.Level:= 0; node_2_min.Level:= 0;
FNodeArr[node_id].copy (node_1_min); // вставляем первый узел на место старого (переполненого) узла FNodeArr[node_id].Parent:= parent_id;
updateMBR (node_id);
new_child_id:= newNode; // создаем новый узел в массиве узлов дерева FNodeArr[new_child_id].copy (node_2_min); // вставляем в только что созданный узел второй узел FNodeArr[new_child_id].Parent:= parent_id; // присваиваем id узла родителя значению parent нового узла updateMBR (new_child_id);
FreeAndNil (node_1); FreeAndNil (node_2); FreeAndNil (node_1_min); FreeAndNil (node_2_min);
if Length (FNodeArr[parent_id].FChildren) < MAX_M then // если хватает места для вставки второго узла begin FNodeArr[parent_id].Children[ High(FNodeArr[parent_id].FChildren) + 1] := new_child_id; // присваиваем id нового узла updateMBR(parent_id); end else // если места не хватает begin splitNodeRStar(parent_id, new_child_id); // вызываем процедуру деления родительского узла end;
end;
procedure TRtree.updateMBR (node: TRNode); var i, idx: Integer; changed: Boolean; begin changed:= False;
node.fmbr.Left.X:= 9999; node.fmbr.Left.Y:= 9999; node.fmbr.Right.X:= 0; node.fmbr.Right.Y:= 0;
if node.isLeaf then begin for i:= 0 to High (node.FObjects) do begin if node.FObjects[i].mbr.Left.X < node.mbr.Left.X then begin node.fmbr.Left.X := node.FObjects[i].mbr.Left.X; changed := True; end; if node.FObjects[i].mbr.Left.Y < node.mbr.Left.Y then begin node.fmbr.Left.Y := node.FObjects[i].mbr.Left.Y; changed := True; end; if node.FObjects[i].mbr.Right.X > node.mbr.Right.X then begin node.fmbr.Right.X:= node.FObjects[i].mbr.Right.X; changed:= True; end; if node.FObjects[i].mbr.Right.Y > node.mbr.Right.Y then begin node.fmbr.Right.Y:= node.FObjects[i].mbr.Right.Y; changed:= True; end; end; end else begin for i:= 0 to High (node.FChildren) do begin idx:= node.FChildren[i];
if FNodeArr[idx].mbr.Left.X < node.mbr.Left.X then begin node.fmbr.Left.X := FNodeArr[idx].mbr.Left.X; changed := True; end; if FNodeArr[idx].mbr.Left.Y < node.mbr.Left.Y then begin node.fmbr.Left.Y := FNodeArr[idx].mbr.Left.Y; changed := True; end; if FNodeArr[idx].mbr.Right.X > node.mbr.Right.X then begin node.fmbr.Right.X:= FNodeArr[idx].mbr.Right.X; changed:= True; end; if FNodeArr[idx].mbr.Right.Y > node.mbr.Right.Y then begin node.fmbr.Right.Y:= FNodeArr[idx].mbr.Right.Y; changed:= True; end; end; end;
if changed then begin if node.Parent >= 0 then updateMBR (node.Parent); end; end;
procedure TRtree.updateMBR (node_id: Integer); var i, idx: Integer; changed: Boolean; begin changed:= False;
FNodeArr[node_id].fmbr.Left.X:= 9999; FNodeArr[node_id].fmbr.Left.Y:= 9999; FNodeArr[node_id].fmbr.Right.X:= 0; FNodeArr[node_id].fmbr.Right.Y:= 0;
if FNodeArr[node_id].isLeaf then begin for i:= 0 to High (FNodeArr[node_id].FObjects) do begin if FNodeArr[node_id].FObjects[i].mbr.Left.X < FNodeArr[node_id].mbr.Left.X then begin FNodeArr[node_id].fmbr.Left.X := FNodeArr[node_id].FObjects[i].mbr.Left.X; changed := True; end; if FNodeArr[node_id].FObjects[i].mbr.Left.Y < FNodeArr[node_id].mbr.Left.Y then begin FNodeArr[node_id].fmbr.Left.Y := FNodeArr[node_id].FObjects[i].mbr.Left.Y; changed := True; end; if FNodeArr[node_id].FObjects[i].mbr.Right.X > FNodeArr[node_id].mbr.Right.X then begin FNodeArr[node_id].fmbr.Right.X:= FNodeArr[node_id].FObjects[i].mbr.Right.X; changed:= True; end; if FNodeArr[node_id].FObjects[i].mbr.Right.Y > FNodeArr[node_id].mbr.Right.Y then begin FNodeArr[node_id].fmbr.Right.Y:= FNodeArr[node_id].FObjects[i].mbr.Right.Y; changed:= True; end; end; end else begin for i:= 0 to High (FNodeArr[node_id].FChildren) do begin idx:= FNodeArr[node_id].FChildren[i];
if FNodeArr[idx].mbr.Left.X < FNodeArr[node_id].mbr.Left.X then begin FNodeArr[node_id].fmbr.Left.X := FNodeArr[idx].mbr.Left.X; changed := True; end; if FNodeArr[idx].mbr.Left.Y < FNodeArr[node_id].mbr.Left.Y then begin FNodeArr[node_id].fmbr.Left.Y := FNodeArr[idx].mbr.Left.Y; changed := True; end; if FNodeArr[idx].mbr.Right.X > FNodeArr[node_id].mbr.Right.X then begin FNodeArr[node_id].fmbr.Right.X:= FNodeArr[idx].mbr.Right.X; changed:= True; end; if FNodeArr[idx].mbr.Right.Y > FNodeArr[node_id].mbr.Right.Y then begin FNodeArr[node_id].fmbr.Right.Y:= FNodeArr[idx].mbr.Right.Y; changed:= True; end; end; end;
if changed then begin if FNodeArr[node_id].Parent >= 0 then updateMBR (FNodeArr[node_id].Parent); end; end;
end.
После реализации все, что оставалось сделать, так это разбить объекты векторной карты по слоям, задать этим слоям максимальный масштаб, при котором они бы отображались и построить для каждого слоя R*-tree.Результаты можно посмотреть на видео:[embedded content]
