[Из песочницы] Простой регулятор на базе нечеткой логики. Создание и настройка
Нечеткая логика для управления
Текст подготовлен на основе материалов книги Гостева В.В. «Нечеткие регуляторы в системах автоматического моделирования». Как все серьезные публикации по теме, данная книга перегружена математическими выкладками и тяжела для неподготовленного читателя. Между тем, сами по себе принципы создания и использования нечеткой логики достаточно просты и наглядны. Данный текст — попытка перевести пример из книги с математического языка на инженерный.
Показана возможную последовательность проектирования регулятора на базе нечеткой логики, путем последовательного усложнения логических правил и подбором параметров методами оптимизации.
Постановка задачи
Рассмотрим синтез цифрового ПИД-регулятора и нечеткого регулятора для системы управления ракетой по углу атаки. Методом математического моделирования определим процессы в системе и дадим сравнительную оценку качества системы при использовании синтезированных регуляторов.
Приняв за выходную координату ракеты угол атаки:  , а за входную координату угол поворота руля
, а за входную координату угол поворота руля 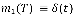 определим передаточную функцию ракеты в виде:
определим передаточную функцию ракеты в виде:  , где:
, где: 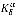 — коэффициент преобразования ракеты,
— коэффициент преобразования ракеты,  — постоянная времени,
— постоянная времени, 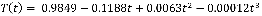 — коэффициент демпфирования.
— коэффициент демпфирования.
При исследовании системы управления предположим, что зависимости параметров ракеты от времени полета определяются так:
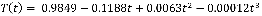
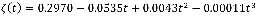
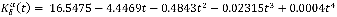
Для упрощения расчетов, рулевой механизм опишем передаточной функцией интегрирующего звена 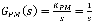 В этом случае вход системы
В этом случае вход системы 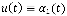 m (t) — управляющий сигнал на выходе регулятора, а объект управления описывается общей передаточной функцией:
m (t) — управляющий сигнал на выходе регулятора, а объект управления описывается общей передаточной функцией:

(В объект управления включены аналоговые рулевой механизм и ракета).
Закон изменения входного воздействия задан полиномом:
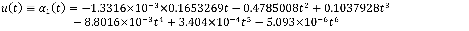
Необходимо разработать регулятор, обеспечивающий отработку входного воздействия с помощью ПИД-регулятора и регулятора на базе нечеткой логики.
Осуществить подбор коэффициентов регуляторов.
Произвести сравнение переходного процесса с ПИД-регулятором и c регулятором на базе нечеткой логики.
Динамическая модель объекта
Создадим динамическую модель в среде структурного моделирования.
Сама схема модели представлена на рисунке 1.
Заданное воздействие задаётся в виде блока константа, в качестве параметров задается переменная из скрипта. Параметры переходной функции задаются в виде переменных.
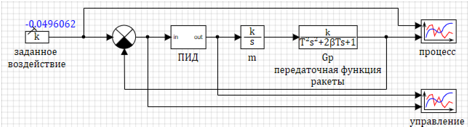
Рисунок 1. Схема динамической модели ракеты.
Настройка регулятора
Блок ПИД представляет из себя субмодель (рис. 2), в котором используется стандартный блок «Дискретный ПИД-регулятор». Частота дискретизации выбрана равной 0.001 сек.

Рисунок 2. ПИД регулятор с схемой настройки.
Параметры регулятора задаются в виде имен глобальных сигналов проекта Kp, Ki, Kd. Это позволяет изменять параметры во время моделирования, и настраивать регулятор.
Для настройки регулятора использовался блок «Оптимизация», критерием оптимизации является минимум среднего квадратичного отклонения.
Блок оптимизации осуществляет оптимизацию по всему переходному процессу. Результат оптимизации — вектор из трех коэффициентов, который направляется в блок «Запись в список сигналов», где вычисленные значения передаются в сигналы и, соответственно, меняются значения коэффициентов ПИД. Для настройки регулятора мы задаём следующие параметры оптимизации:
Исходные значения всех коэффициентов 1.
Диапазон для подбора задан от -50 до +50
Точность подбора 0.001
Максимальное среднеквадратичное отклонение после оптимизации 0.01
В рассматриваемом случае блок оптимизации рассчитал следующие оптимальные значения коэффициентов:
Kp = -1,7498597; Ki = 17.891995; Kd = 11.606602.
При таких коэффициентах среднеквадратичное отклонение в заданном переходном процессе составило 0.008738090
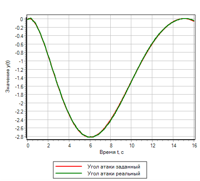 Рисунок 3. Переходной процесс. |
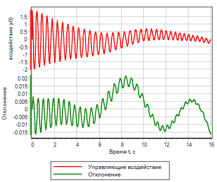 Рисунок 4. Управление. |
Регулятор на базе нечеткой логики
Основное преимущества регулятора на базе нечеткой логики — это простота и наглядность формирования правил управления объектом.
Для примера, в книге «Нечеткие регуляторы в системах автоматического моделирования», правила нечеткого регулирования для управления ракеты по углу атаки описаны в виде математического выражения:
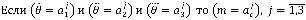
где, 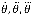 — ошибка системы, скорость изменяя (первая производная) ошибки, ускорение (вторая производная) ошибки;
— ошибка системы, скорость изменяя (первая производная) ошибки, ускорение (вторая производная) ошибки;
m — управляющие воздействие на объект;
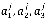 -лингвистические оценки ошибки, скорости изменения ошибки (первой производной) ошибки и второй производной ошибки, рассматриваемые как нечеткие множества, определенные на универсальном множестве
-лингвистические оценки ошибки, скорости изменения ошибки (первой производной) ошибки и второй производной ошибки, рассматриваемые как нечеткие множества, определенные на универсальном множестве 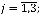
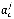 — лингвистические оценки управляющего воздействия на объект, выбираемые из терм-множеств переменной m
— лингвистические оценки управляющего воздействия на объект, выбираемые из терм-множеств переменной m
Читатель может спросить: это как же, вашу мать, извиняюсь, понимать?
Иногда у меня закрадываются сомнения в том, что авторы-математики сами понимают то, что они написали. За заумными математическими оборотами спрятана великая тайна правил нечеткого регулирования. Вот она:
много — уменьшай
норма — не трогай
мало — увеличивай
Если перевести с птичьего языка математики на русский, то выражения
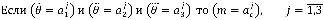 означает буквально следующее:
означает буквально следующее:
Если больше нормы и отклонение растет и скорость роста увеличивается, то уменьшаем.
Если норма, и не изменяется и скорость постоянна, то не изменяем.
Если меньше нормы и падает и скорость падения увеличивается, то увеличиваем.
Если понимать то, что реально скрывается за математическим туманном, то можно подходить к созданию регуляторов более осознано и получить более интересные результаты.
Немного теории
Для решения задачи регулировании угла атаки мы должны из непрерывной величины отклонения получить три терма — меньше, норма, больше. То же самое нужно сделать для первой производной отклонения и второй производной отклонения. Это первый этап нечеткого вывода — фазификация.
Чтобы получить термы, мы должны задать числовое значения параметра для каждого терма. Например: «Мало» = -1; «Норма» = 0; «Много» = 1. Для фазификации будем использовать треугольные функции. Функции растут по мере приближения к заданной величине, и уменьшаются по мере удаления. Два варианта треугольных функций приведены на рисунке 5: 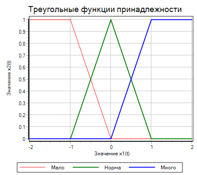
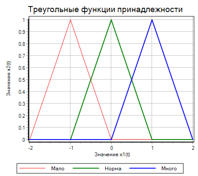
Рисунок 5. Треугольные функции принадлежности.
Зная величину отклонения (х1), мы можем найти значения функции принадлежности для термов больше (красная линия), норма (зеленая линия), меньше (синяя линия). Величины будут находится в диапазоне от 0 до 1.
Обратите внимание, что на левом графике крайние функции, не совсем «треугольные». Если рассматривать с точки зрения абстрактной математики, то функции на правом графике более «красивые». Но, если вспомнить «главную тайну правил нечеткого вывода», то левый график более правильный. В самом деле:
Рассмотрим правило «Мало — добавляй», если у нас значение -1, то «мало» = 1 (красная линия) верно для обоих графиков. А если у нас значение -2? По логике мы тоже должны «добавлять». На левом графике при -2 так и есть: «мало = 1», но на правом графике у нас «мало» = 0, что очевидно не верно. То же самое справедливо для правила «Много — уменьшай».
Фазификация «честными» треугольными функциями может приводить к тому что при выходе величины за диапазон определения функций мы получаем 0, для всех термов, что, в свою очередь, может приводит к отсутствию воздействия на объект.
Обратная задача — дефазификация. Для расчета воздействия нужно выполнить обратное преобразование — у нас есть значения функций принадлежности уменьшать, не изменять, увеличивать в диапазоне (0…1) (треугольные функции) и диапазон воздействий, которые мы можем оказать, и мы должны из трех термов получить одно число — конкретное воздействие.
Получить можно воздействие можно различными способами, например, по центру массы фигуры. На рисунке 6 приведено состояние регулятора, где значения термов уменьшать 0.3 не изменять 0.6 и увеличивать 0.8 при диапазоне регулирующего воздействия -30…30 результирующие воздействие = 4.1.
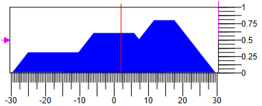
Рисунок 6. Дефазификация управляющего воздействия
Другой вариант дефазификации — по центру масс точек. На рисунке 7 приведен вариант, где при тех же значениях термов и диапазону регулирования, мы получаем другой вариант ответа 8.82:
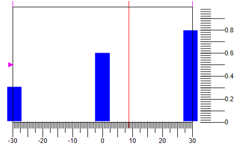
Рисунок 7. Дефазификация методом центра массы точек.
Надо понимать, что кроме способа вывода, на результат влияет также форма функции принадлежности. Например, можно выбрать такие треугольные функции, у которых основание треугольника одинаковое, отличаются только вершины. (см. рис. 8).
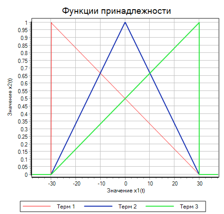
Рисунок 8. Треугольные функции принадлежности с одним основанием.
В этом случае результат фазификации при таких же значениях термов уменьшать 0.3, не изменять 0.6 и увеличивать -0.8 при диапазоне регулирующего воздействия -30, 30 результирующие воздействие = 5.27.
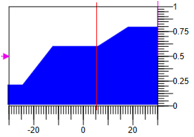
Рисунок 9. Дефазификация методом расчета площади.
Вооружившись тайными знаниями о нечеткой логике, создадим модель регулятора. Модель ракеты оставляем такую же как и для ПИД-регулятора (см. рис. 1), а вот в субмодели регулятора соберем схему, изображенную на рисунке 10.
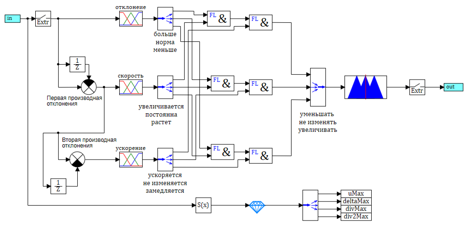
Рисунок 10. Схема регулятора на базе нечеткой логики.
На вход в регулятор подается рассогласование между заданным углом атаки и реальным (измеренным). После входа стоит блок «Экстраполятор», который обеспечивает преобразование непрерывного сигнала в дискретный с заданным периодом дискретизации (0.001 с — такой же, как у дискретного ПИД-регулятора).
После этого происходит вычисление первой и второй производной отклонения. Для этого мы вычисляем разность межу текущем значением и значением с задержкой на период квантования, делим ее на время задержки (коэффициент в сравнивающем блоке). Таким образом мы получаем три входа: ошибка системы, скорость изменения (первая производная) ошибки, ускорение (вторая производная) ошибки.
Значение входных переменных преобразуются блоками фазификации треугольными функциями. Для каждой переменной получаем три лингвистические переменные (всего девять).
Блоки «Демультиплексор» разводят вектора в лингвистические переменные для формирования правил. На схеме названия переменных подписаны в порядке их распоряжения в векторах.
Отклонение в нашем случае — это разность заданного и измеренного, если отрицательное значение — значит угол атаки больше заданного, мы должны уменьшать. И соответственно наоборот, если отклонение положительно, то измеренный угол меньше заданного, мы должны увеличивать.
(Больше — уменьшай, меньше — увеличивай, норма — не трогай).
Выход тоже имеет три лингвистические переменные «уменьшать», «не изменять», «увеличивать». Мультиплексор собирает значения в вектор и отдает в блок нечеткого вывода. Теперь, когда у нас есть все переменные, мы можем записать правила нечеткого вывода в виде схемы.
- Если больше нормы и отклонение растет и скорость роста увеличивается => уменьшаем.
- Если норма и не изменяется и постоянна => не изменяем.
- Если меньше нормы и падает и скорость падения увеличивается => увеличиваем.
Все лингвистические переменные в правилах у нас связаны через логические блоки «и» и подключены к выходам. Как видно из рисунка 10, схема логическая нечеткого вывода практически не отличается от обычной логической схемы, только используются блоки нечеткой логики.
Аналогично настройке ПИД-регулятора, мы используем блок оптимизации.
Остается вопрос с параметрами блоков.
Синтез регулятора на базе нечеткой логики
В жизни ничего не дается даром и поэтому, простота правил регулирования, компенсируется количеством параметров, описывающих функции принадлежности. В самом деле, если для ПИД-регулятора нужно подобрать три коэффициента, то в случае нечеткой логики, только для одной треугольной функции нужно 3 числа для вершин. Если для каждой входной переменной нам нужно 3 функции принадлежности + 3 для выходной, получается, что нам нужно задать 3×3 x 3 + 3×3 = 36 параметров!
Но не все так печально. Для первого приближения и первичной настройки можно все упростить.
Сделав некоторые допущения для первоначальной настройки регулятора:
- Задаем симметричность функций, относительно нуля, тогда вместо двух чисел для максимума и минимума можно задать одно — Мах, и, соответственно диапазонно будет определен как [-Мах… Мах].
- Задаем, равномерное распределение функций, тогда можно рассчитать положение всех вершин треугольников исходя из заданного диапазона.
- Для трех функций координаты вершин определятся как –Max, 0, Max.
- Задаем, что основание треугольника всех функций принадлежности одинаковы.
Таким образом, вместо 36 независимых параметров мы должны задать только 4, максимальное отклонение от 0 для трех входных переменных и одного выхода, а именно:
uMax — амплитуда управляющего воздействия (-uMax… uMax);
deltaMax — максимальное отклонение (-deltaMax… deltaMax);
divMax — максимальная производная отклонения (-divMax… divMax);
div2Max — максимальная вторая производная отклонения (-div2Max… div2Max)
В функциях фазификации и нечеткого вывода используем эти сигналы для расчёта параметров с учетом принятых допущений.
Настройки регулятора, предложенные в книге Гостева В.В. «Нечеткие регуляторы в системах автоматического моделирования», для случая фазификации тремя функциями принадлежности предлагаются следующие параметры:
uMax = 30 — амплитуда управляющего воздействия;
deltaMax = 0.01 — максимальное отклонение;
divMax = 0.07 — максимальная производная отклонения;
div2Max = 1 — максимальная вторая производная отклонения.
Сравнение переходных процессов
На графике переходных процессов совпадение заданного воздействия и полученного результат практически полное:
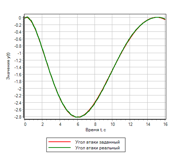 Рисунок 11.а Переходной процесс. ПИД регулятор |
 Рисунок 11.б Переходной процесс. Нечеткая логика |
Явные отличия можно посмотреть на графиках полученного отклонения и управляющего воздействия:
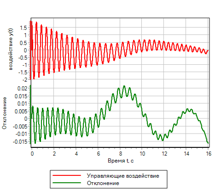 Рисунок 12.а. Управление. ПИД регулятор |
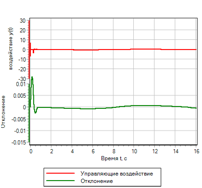 Рисунок 12.б. Управление. Нечеткая логика |
Из сравнения рисунков видно, что нечеткий регулятор обеспечивает меньшую ошибку, и лучше отрабатывает переходной процесс.
Сравним переходные процессы в системе, если задать ступенчатое управляющее воздействие. Результаты на рисунке 13:
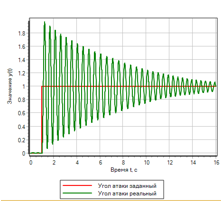 Рисунок 13.а. Ступенчатое воздействие. ПИД регулятор. |
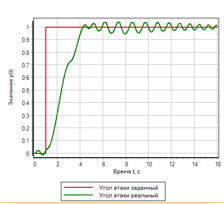 Рисунок 13.б. Ступенчатое воздействие. Нечеткая логика. |
Для ступенчатого воздействия, регулятор на основе нечеткой логики обеспечивает лучшее качество переходного процесса. ПИД-регулятор, настроенный автоматически на плавный процесс, вызывает колебания с перерегулированием в два раза превосходящие заданную ступеньку.
Настройка регулятора на базе нечеткой логики методом оптимизации
Попробуем подобрать параметры нечеткого регулятора методом оптимизации, так же как мы подбирали их для ПИД-регулятора. В качестве критерия зададим средне квадратичное отклонение менее 0.001.
Надо заметить, что данный метод не совсем правильный, поскольку для профессионалов понятно какие углы и какие скорости являются максимальными и минимальными для каждого концертного изделия, что позволяет задавать ограничения на оптимизируемые параметры более осознанно, мы же задаем параметры по умолчанию и смотрим, что получается.
Метод оптимизации с настройками по умолчанию рассчитал следующие значения диапазонов параметров оптимизации:
uMax = 19.377 — амплитуда управляющего воздействия;
deltaMax = 1.095 — максимальное отклонение;
divMax = 0.01 — максимальная производная отклонения;
div2Max = 2.497 — максимальная вторая производная отклонения.
В случае простой оптимизации по отклонению, полученные параметры обеспечивают заданную точность, однако при этом вызывают высокочастотные колебания управляющего воздействия.
Переходная функция и управляющие воздействия представлены на рисунке 14.а
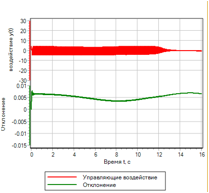 Рисунок 14.а. Нечеткая логика. Настройка по отклонению. |
 Рисунок 14.б. Нечеткая логика. Настройка по отклонению и количеству срабатываний. |
Для того, чтобы улучшить переходной процесс, можно добавить в критерий оптимизации количество переключений регулятора с отрицательного на положительное значение регулирующего воздействия (схема на рис. 15).

Рисунок 15. Схема для оптимизации по 2 критериям.
Расчет методом оптимизации по двум критериям дает следующие значения параметров:
uMax = 19.714 — амплитуда управляющего воздействия;
deltaMax = 1.0496 — максимальное отклонение;
divMax = 0.01 — максимальная производная отклонения;
div2Max = 1.7931 — максимальная вторая производная отклонения.
Видно, что при добавлении в критерий оптимизации числа срабатываний, удалось сократить частоту переключения регулятора (см. рис. 14.б). Таким образом можно сказать, что метод оптимизации работает, даже когда мы ничего не знаем о физике объекта и просто подбираем числовые параметры, не задумываясь об их физическом смысле.
Создание собственного регулятора на базе нечеткой логики
Выше мы создали регулятор по уже готовой и достаточно простой схеме, все термы лингвистических переменных соединили логическим оператором И. Поскольку у нас количество термов на входах и выходах одинаково, то это самое простое и очевидное решение.
Попробуем сделать регулятор, у которого на выходе не 3 терма, а, например, 5: уменьшать быстро, уменьшать, не изменять, увеличивать, увеличивать быстро. А на входе те же самые.
Изменим логику работы регулятора, для начала максимально упростив алгоритм управления.
Запишем правила:
1) Если больше и растет => уменьшать быстро.
2) Если больше =>уменьшать.
3) Если норма => не изменять.
4) Если меньше => увеличивать.
5) Если меньше и уменьшается => увеличивать быстро.
В этом случае у нас для выходной переменной 5 термов (5 треугольных функций). Принимаем, что они распложены равномерно между -uMax и +uMax.
Принимаем, что треугольные функции составлены таким образом, что когда функции принадлежности терма принимает максимальное значения, соседние функции принимают нулевые значения (см. рис. 5).
В качестве параметров для вывода будут использоваться только отклонение и скорость изменения отклонения.
Для ускорения расчетов используем фазификацию вывода методом центра тяжести точек (см.рис. 7).
Схема регулятора в этом случае будет в выглядеть как показано на рисунке 15.
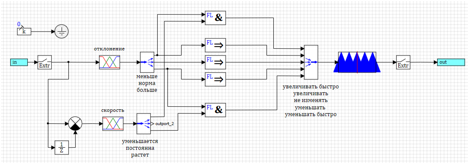
Рисунок 15. Упрощенный регулятор на базе нечеткой логики.
Вместо диапазона второй производной оптимизатора будет побираться значение для терма «увеличивать». Попытка настроить подобный регулятор методом оптимизации показывает, что регулятор настраивается, но качество регулирования управления системой оставляет желать лучшего.
Наилучший результат показан на рисунке 16.
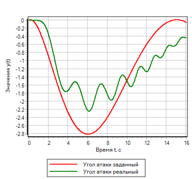
Рисунок 16. Переходной процесс для упрощенного регулятора.
Видно, что регулирование происходит, однако совсем не так как нам бы хотелось. Дело в том, что мы осуществляем воздействие, когда уже произошло отклонение. Попробуем включение регулирования в моменте, когда у нас отклонение в норме, но скорость показывает, что оно будет расти или уменьшатся.
1) Если меньше и уменьшается => увеличивать быстро.
2) Если норма и увеличивается => уменьшать.
3) Если норма => не изменять.
4) Если норма и уменьшается => увеличивать.
5) Если больше и растет => уменьшать быстро.
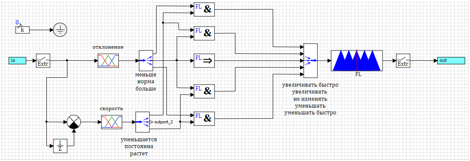
Рисунок 17. Управление по скорости изменения отклонения.
Результаты работы регулятора настроенного методом оптимизации, представлены на рисунках 18а и 18 б.
 Рисунок 18.а. Переходной процесс. |
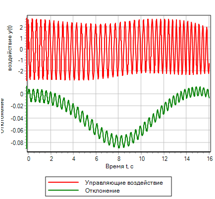 Рисунок 18.б. Управление |
Управление по скорости изменения отклонения значительно улучшило переходной процесс. Однако, если внимательно посмотреть на набор логических правил, то мы видим что отклонение не участвует в управлении. Если дать ступенчатое воздействие, контроллер управления не будет формировать управляющее воздействие. На рисунках 19 приведен пример переходного процесса при ступенчатом управляющем воздействии, видно, что регулятор не выдает управляющего воздействия, хотя отклонении равно 1.
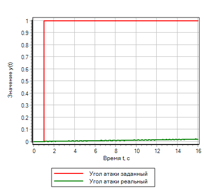 Рисунок 19.а. Переходной процесс. Ступенька |
 Рисунок 19.б. Управление. Ступенька |
Для того, чтобы отработать быстрые отклонения, добавим управляющее воздействие при отклонении. Будем увеличивать, если меньше и уменьшать, если больше. Поскольку в наборе правил уже есть правила, при которых мы уменьшаем и увеличиваем, мы используем логический оператор или:
1) Если меньше и уменьшается => увеличивать быстро.
2) Если (норма и увеличивается) или больше => уменьшать.
3) Если норма => не изменять.
4) Если (норма и уменьшается) или меньше => увеличивать.
5) Если больше и растет => уменьшать быстро.
Схема регулятора по данным правилам представлена на рисунке 20.
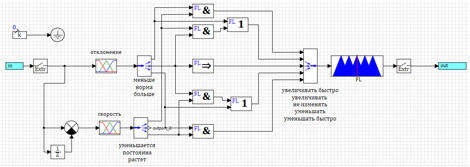
Рисунок 20. Регулятор с управлением по отклонению и скорости изменения.
В результате модификации, качество переходного процесса при плавном воздействии практически не изменилось, однако при ступенчатом воздействии регулятор начал отрабатывать ступеньку и приводить угол атаки ракеты к заданному (см. рис. 21).
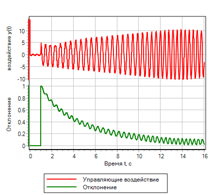 Рисунок 21.а. Переходной процесс. Ступенька |
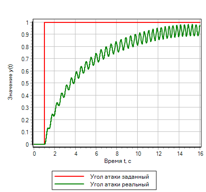 Рисунок 21.б. Управление. Ступенька |
В заключение, давайте еще раз «улучшим» наш регулятор.
Попробуем использовать вторую производную отклонения, для начала воздействия, до того как изменилось отклонение и его скорость. В самом деле, при приложении силы, у нас появляется ускорение, на которое уже можно реагировать.
Попробуем добавить в закон регулирования вместо первой производной скорости, вторую производную. Будем оказывать дополнительно регулирующее воздействие в случае, когда у нас вторая производная показывает, что будет отклонение. Общие правила будут выглядеть практически так же, только в скобках у нас три терма, отклонение и скорость в норме, а отклоняется вторая производная:
1) Если меньше и уменьшается => увеличивать быстро.
2) Если (норма и постоянна и разгоняется) или больше => уменьшать.
3) Если норма => не изменять.
4) Если (норма и постоянна и замедляется) или меньше => увеличивать.
5) Если больше и растет => уменьшать быстро.
Схема данного регулятора приведена на рисунке 22. Для экономии места на схеме логические выражения «и», записанные в правилах в скобках, вычисляются в субмодели, обозначенной »&».
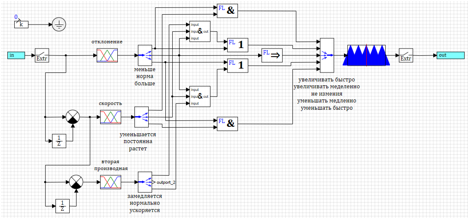
Рисунок 22. Регулятор нечеткой логики с контролем второй производной.
После подбора параметров методом оптимизации по отклонению и количеству включений, получены следующие параметры:
uMax = 27.4983 — амплитуда управляющего воздействия;
deltaMax = 0.0433— максимальное отклонение;
divMax = 0.0966 — максимальная производная отклонения;
div2Max = 1.0828 — максимальная вторая производная отклонения.
Переходной процесс показан на рисунке 23. Видно, что полученный регулятор обладает наилучшими показателями из всех рассмотренных выше, но для заданного воздействия. Отклонения и управляющие воздействия — минимальные из всех рассмотренных в данном тексте.
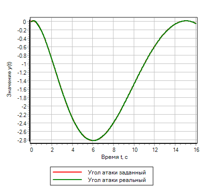 Рисунок 23.а. Переходной процесс. |
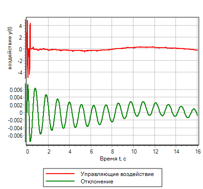 Рисунок 23.б. Управление. |
Выводы
Регулятор на базе нечеткой логики может обеспечить более высокое качество переходного процесса для управления ракетой, чем ПИД-регулятор.
Настройку регулятора на базе нечеткой логики можно осуществлять средствами оптимизации.
Регулятора на базе нечёткой логики обеспечивает большую гибкость в настройке и лучшее качество переходного процесса. Но требует настройки большего количества параметров.
Скачать архив моделей, использованных при подготовки данного текста, для самостоятельного изучения можно здесь…
