[Из песочницы] Попытки открытия новой шашечной тактики или что делать с несбыточной мечтой22.12.2016 14:34

Введение

Спортивная игра «Шашки» является одной из игр человечества, которые компьютер ещё не просчитал полностью. Есть новости о том, что ученые нашли стратегию, при которой компьютер никогда не проиграет. За свои 9 лет, посвящённых этой игре, я встретил лишь одну программу, которую никак не мог выиграть. Пожалуй, мой спортивный опыт позволит сделать предположение, что это была программа реализующая стратегию описанную выше. К моему большому удивлению, она занимала лишь 60 Мбайт. А может быть, там была хорошо обученная нейронная сеть в основе? Но всё же мне не верится, что просчитать их невозможно. Там всего лишь 10^20 позиций, неужели мой компьютер не справится с такой задачей? А также, неужели нет тактики, в которой в начале партии соперник отдаёт шашку и оказываются в тактическом преимуществе?! Ни одного дебюта такого я не встречал. Пойду проверю…

Реализация алгоритма для решений комбинационных задач

Первая попытка была предпринята в конце 2-го курса. После качественного изучения языка Си, я считал, что не помешало бы изучить С++. После просмотра большого количества лекций по данному языку, я хотел взяться за какой-нибудь проект. И взялся за шашки. Более тонкая работа с переменными позволила более рационально тратить время на просчёт позиций. Если данные действия уподобить действиям с графами, то этот алгоритм можно было бы назвать поиском в ширину. Остановкой работы алгоритма являлось полное прохождение по графу.

Один объект описывал сложившуюся ситуацию на доске. В одном объекте хранилось:

class Queue
{
public:
Queue *pnr;	/*pointer to next record*/
Queue *ppr;	/*pointer to prev record*/
Map *pdb;	/*pointer to draught board*/
char *action;	/*actions of parents*/
Queue *pp;	/*pointer to parent*/
Queue *pfc;	/*pointer to first child*/
int nmd;	/*Approval of the number of moves to a draw*/
int color;
};

Так как здесь был реализован алгоритм поиска в ширину, то данные можно было складировать в двусвязный лист, где pnr и ppr указатели реализующие эту коллекцию.

pdb — Указатель на расстановку доски.
action — данные о ходе совершённом родителем, для того, чтобы достичь эту позицию. Она выглядела как обычная запись ходов в шашках «c3–d4» при передвижении шашки или «c3: e5» при срубе. Переменная была необходима для более точной отладки сложившейся ситуации.
pp, pfc — указатели на родителя и на первую порождённую позицию. Т.к. алгоритм поиска был реализован в ширину, то все порождённые позиции в двусвязном списке располагались рядом, один за другим. Поэтому для того, чтобы сохранить данные в виде дерева достаточно хранить указатель на первого дитя, а все остальные последующие дети ссылались на одного и того же родителя. Данный алгоритм позволял извлекать родителю результаты детей, то есть анализировать текущую ситуацию, смотря лишь на то, к чему может привести тот или иной ход породивший ребёнка.
nmd — Число показывающее, сколько ходов осталось, до того, как партия будет считаться ничейной. Например, при ситуации 3-ёх дамок против 1-ой, на завершение партии выделяется лишь 15 ходов. При изменении количества шашек, а также после становления шашки дамкой данное число пересчитывается.
color — Чей сейчас ход.

Я очень боялся переполнения стека и считал, что передавать указатели в функции будет всё же лучше, поэтому решил избегать прямой передачи объекта в качестве параметра. Реализация была проста: берём элемент из очереди, рассматривает его, порождая последующие позиции, затем брали следующий элемент из очереди и так по кругу.

Результат:

Просмотрено: 61.133 позиций
Хранится записей в очереди: 264.050 позиций
Оперативная память (2 ГБ) закончилась лишь на таких данных. Такие результаты подходят лишь для коротких комбинационных задач.
Зато такой способ работы с шашечными позициями позволил тщательно отладить работу «ядра» программы.

Переход к «системе контроля версий»

В алгоритме очень много памяти уходило на сохранение данных о доске. Каждая позиция требовала выделить участок памяти. Тем более, как закодировать текущую шашечную расстановку лучше, я не придумал:

/* info about one checker */
class Checkers
{
public:
chlive live;
chstatus status;
};

/* info about position a checker */
class PosCheckers
{
public:
chcolor color;
Checkers *ptrCheckers;
};

/* battlefield */
class Map
{
public:
PosCheckers coordinate[8][8];
};

color — Цвет шашки. Чёрная, белая, либо пусто.
ptrCheckers — Если шашки на данном поле нет, то не выделяем память.
status — Дамка или шашка.
live — Жива ли шашка. Лишь для того, чтобы не срубить эту шашку повторно.

Понимаю, что вместо coordinate[8][8] можно было обойтись лишь coordinate[8][4], но понимание собственного кода бы весьма сильно пострадало.

В общем, очень много памяти требовалось на сохранение позиции, поэтому я решил возложить ответственность за идентификацию позиций шашек на action — запись о ходе родителя, в которой содержались данные типа «c3-d4».

Теперь, когда берём элемент из очереди, мы, начиная с самого начала. Берём исходную позицию шашек и от неё уже по обратному пути, выполняем ходы, привлёкшие к этому ребёнку. Так строилась расстановка шашек на доске для каждого элемента очереди.

Результат:

Просмотрено: 1.845.265 позиций
Хранится записей в очереди: 8.209.054 позиций

Отказ от «системы контроля версий»; переход к поиску в глубину

К сожалению, у поиска в ширину было как минимум несколько существенны проблем: Иногда он создавал одинаковые расстановки партий. А распознать, уже созданную партию, при большом количестве данных, было трудоёмко. Также не понятно было, что делать, когда нам не хватало памяти. Все хранящиеся данные были необходимы, чтобы восстановить идеологическую цепочку, так что при необходимости «черпнуть» откуда-нибудь памяти, её не оказывалось.

Поиск «в глубину» позволил перейти от задач локального характера (решений комбинационных задач) к глобальным (просчёт всей партии). Данный алгоритм рассматривает текущую расстановку шашек, порождая потомков, выбирает из них первого и назначает его на роль текущего. Если потомков нет, то указываем, что в данной позиции мы проиграли и переходим рассматривать следующую расстановку у родителя.

Также дабы не просчитывать повторные позиции при наличии дамок, было решено просматривать все позиции-родители. При наличии таковой я не рассматриваю её, а перехожу к следующей.

Было решено убирать из памяти правнуков у расстановки, у которой был известен результат. Тем самым можно было избежать её переполнения. Если же переполнения не произойдёт при поиске самого глубинного элемента.

Также было решено добавить новый способ хранения позиции — список из фигур:

class ListCheckers
{
public:
ListCheckers *pnr;
chcolor color;
chstatus status;
int x,y;	/* coordinate */
};

При помощи него мы стали более быстро находить возможность сруба, а также перебирать шашки для проверки возможности хода. Теперь наш объект «позиция» хранившийся в очереди, имел такие поля:

class Queue
{
public:
ListCheckers *plch;	/*pointer to list of checkers*/
ListChilds *pcs;	/*pointer to list of childs*/
chcolor color;
int draw;
chresult result;
};

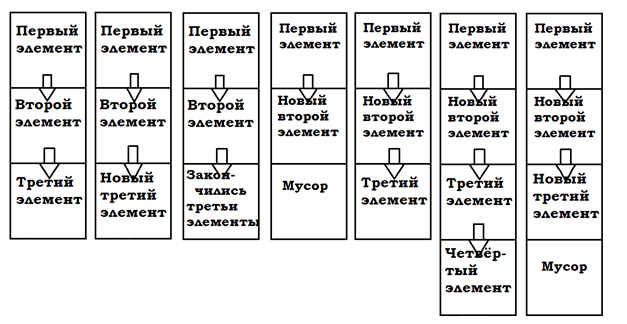
Я никак не ожидал, что команда free не гарантирует 100% освобождения памяти. При отладке выяснилось, что после выполнения команды free память не освобождалась вовсе. Где-то в потёмках форумов я узнал, что free лишь подаёт инструкцию ОС об освобождении памяти, а уже ОС сама решает, освобождать ли память или нет. В общем, ОС у меня оказалась «жадной», поэтому пришлось работать с памятью по-другому. Я выделял память по мере необходимости для удержания цепочки из первых «детей». А вместо удаления «первого» ребёнка, которого мы просмотрели, данные о нём перезаписывались данными о следующем ребёнке.

Для этого был разработан элемент отвечающий за динамическую работу с памятью:

class MainQueue
{
public:
MainQueue* parent;	/*pointer to parent’s record*/
MainQueue* next_record;	/*pointer to child’s record*/
Queue* now;	/*pointer to record on data with position*/
int draw;
};

Результат:

За 1 день непрерывной работы:
создано было 2.040.963 партии
просмотрено было 1.241.938 партии
Занимаемое место на оперативной памяти: 1.378 МБ

Работа с файлами

К сожалению, при таком выборе следующего элемента мы подолгу бы «подвисали» с одинаковыми позициями. Особенно при просчётах для дамок. Поэтому хотелось реализовать базу данных, где хранились бы результаты уже просмотренных позиций. Поэтому я решил хранить данные о каждой партии.

Уходя от проблемы с памятью, я снова с ней столкнулся. Так как оперативной памяти мне не хватало, я решил использовать внешний носитель. Все позиции я записывал в файл index.txt и queue.txt. В queue.txt у меня хранились данные о каждой партии. А в index.txt — идентификатор партии и расположение информации о этой партии в queue.txt, то есть смещение. Хотелось сжать данные, но оставить их в читабельном виде. Потому что я считал, что до финиша было всё равно далеко. Поэтому я сохранял данные в таком виде:

queue.txt :
aaaaeaaaaacaaaaa aaaaeaaaaaakaaaa 50 U
Aaaaaaeaaacaaaaa Aaaaaaauaacaaaaa 49 U
aaaaaaeakaaaaaaa aaaaaaeacaaaaaaa 48 W
Aaaaaaaaaauaaaaa 47 L
…

index.txt :
Aaaaeaaaaaaacaaa000000000000000000000
aaaaeaaaaacaaaaa000000000000000000040
aaaaeaaaaaakaaaa---------------------
Aaaaaaeaaacaaaaa000000000000000000080
Aaaaaaauaacaaaaa000000000000000000178
…

На доске игровая клетка может принимать 5 состояний: белая/чёрная шашка, белая/чёрная дамка, либо пусто. Значит, у двух клеток будет 25 состояний в различных комбинациях. Заметим, что в латинском алфавите 26 букв и он вполне подходит, для того, чтобы одной буквой описать состояние сразу 2-ух игровых клеток. Значит, что всю доску с 32-мя игровыми клетками можно описать 16-ю буквами латинского алфавита, которые имеют более-менее читабельный вид. Также на необходимо сохранить, чей в данной позиции ход. Тогда, пускай, если первая буква будет заглавной, то ход сейчас чёрных. Также нам следует запомнить количество ходов от текущей расстановки, до принятия позиционной ничьи. А также и результат: W-win, L-lose, D-draw, U-unknown. И отлаживаться не стало сложней.

Результат:

За два часа программа потребовала лишь 4 MB оперативной памяти, но партий просчитала крайне мало. В queue.txt находилось 2918 записей и равен был 401 КB. Файл index.txt содержал 6095 записей и весил 232 KB. С такими темпами получится просчитать лишь 500 млн = 5×10^8 позиций и мой диск в 1TB сообщил, что памяти у него не достаточно. Да и произойдёт это весьма и весьма не скоро. Мои просчитанные позиции слабо скажутся на всю игру в целом.

Сжатие данных

Я смог придумать лишь 3 варианта продвижения проекта:

5^32 — различных расстановок фигур,
2×5^32 — учитывая, чей ход
2*(2×5^32) — максимальное количество занимаемого места ~ 9,32×10^22 бит при условии, что достаточно будет у каждой расстановки указать результат равным в 2 бита.
Причём, в обычной партии имеется 5×10^20 различных позиций.
А значит, около 2*(2×5*10^20) = 2×10^21 бит будут информационными, а остальные ~(9,12×10^21) будут обозначать, что такой расстановки шашек в данной партии не существует.
В распоряжении имеется 1TB = 8×10^12 бит
Необходимо разработать алгоритм сжатия для данной задачи, сохранив быструю индексацию данных.
В обычной партии имеется 5×10^20 различных позиций.
Для быстрой индексации сохраним у каждой позиции её «детей», а также результат. В среднем у позиции около Y потомков.
Закодируем «ссылки» на потомков в Х бит, а результат в 2 бита, а также разделитель между записями в Z. Получаем (Х*Y+2+Z) бит на каждую позицию. Итого (Х*Y+2+Z)*5×10^20 бит требуется выделить для хранения всех позиций, используемых в начальной расстановке.
В распоряжении имеется 1TB = 8×10^12 бит
Необходимо разработать алгоритм сжатия для данной задачи, сохранив быструю индексацию данных.
Попробуем найти повторяющиеся закономерности в записях и реализовать замену повторов на более короткие записи. Идейно алгоритм похож на код Хаффмана.
Отрицательно скажется на не столь быстрой индексации.

Итого нужно сжать данные c ≈10^22 до 10^13 бит. А значит, необходимо было написать алгоритм, который позволил бы сжимать данные всего лишь на 99.9999999914163%. Сомневаюсь, что какой-либо алгоритм на это способен, причём, не учитывая ещё, что необходимо сохранить быструю индексацию.

Результат:

Сохранение каких-либо данных обо всех партиях совсем не применимо.

Возврат к работе проекта только на оперативной памяти. Создание «процессора»

Было принято хранить данные, которые хранились в файлах, в оперативной памяти. Для этого было решено изменить структуру хранения данных:

class list_strings
{
public:
list_strings* next;
char* data;

list_strings()
{
data = new char[17];
data[0] = '\0';
next = nullptr;
}
};

class Queue
{
public:
ListCheckers *plch;	/*pointer to list of checkers*/
list_strings *pcs;	/*list of data of childs*/
chcolor color;
chresult result;
int to_draw; 
}

А также изменён принцип хранения объекта Queue. После того, как перезаписывался MainQueue, перезаписывается и объект Queue, на который указывает MainQueue.

Поле «pcs» предназначенное для хранения «детей» теперь реализовано как односвязный список с данными типа «Aaaaaaeaaacaaaaa», расширяющийся по мере необходимости. Дабы использовать выделенную память повторно (при перезаписи) поля с данными становились равными »\0» — нулю, для обозначения того, что поля не содержат важную информацию. Т.к. «объект» изменился.

Результат:

Максимальное занимаемое место на оперативной памяти: 844 КБ. Запуск на 7 часов позволил просмотреть 8.865.798.818 позиций. Но, позиции могут повторяться. Данные результаты являются недостаточным, для достижения полного просчёта партии за приемлемое время выполнения.

Теперь можно сказать, что есть «процессор», который будет перемалывать позиции и ему потребуется лишь 844 КБ оперативной памяти, а значит, оставшуюся память можно потратить с пользой, например, реализовать «cash-память», дабы не просчитывать позиций, которые уже просчитаны.

Создание «cash-памяти»

Для наиболее быстрой выборки данных из памяти была выбрана hash-таблица, заполоняющая максимально-возможное пространство в оперативной памяти. В качестве hash-функции были выбраны последние числа алгоритма md5, на вход которой подавалась зашифрованное описанное позиции. То есть позиция «Aaauaueaaacckaaa» с md5 0237d0d0b76bcb8872ecc05a455e5dcf будет хранится по адресу: f * 2^12 + c * 2^8 + d * 2^4 + 5 = 15×4096 + 12×256 + 13×16 + 5 = 64725.

Единицей хранения записи в hash-таблице была ячейка. Данный подход позволяет удалять данные из «устаревших» ячеек и использовать их пространство повторно. «Устаревание» реализовано при помощи кольцевого буфера:

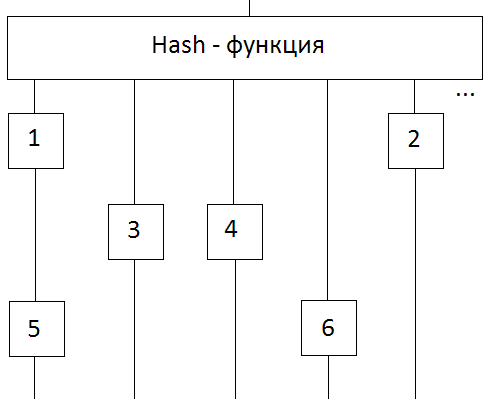
По первому адресу в cash-памяти хранятся ячейки №1 и №5, во второй №3… А в кольцевом буфере ячейки хранятся в хронологическом порядке. Если бы максимум мы могли хранить 5 ячеек, то ячейку с №1 «выдернули» из того места, где находится сейчас и поместили бы на место 6-ой ячейки. Причём, теперь в cash-памяти по первому адресу будет храниться только ячейка №5.

class mem_cel
{
public:
mem_cel* pnhc; /* pointer to next in hash collection */
mem_cel* pphc; /* pointer to prev in hash collection */
mem_cel* pnrb; /* pointer to next "mem_cel" record in ring buffer */
mem_cel* pprb; /* pointer to prev "mem_cel" record in ring buffer */
chresult result;
int draw;
stringMap condition;
};

Поле condition необходимо для идентификации искомой расстановки шашек, потому что различные расстановки могут храниться по одному и тому же адресу cash-памяти.

Поле draw необходимо для выявления совпадения запроса. Если в памяти хранится ничейный результат позиции, для которой было выделено лишь 3 хода, то при наличии большего количества ходов можно как добиться выигрыша, так и успеть проиграть.

Результат:

Запуск на 1 час позволил просмотреть 10.400.590 позиций. Необходимо реализовать что-то, позволяющее ускорять данный просчёт. Но, если производить расчёты, то мой компьютер, в лучшем случае, будет вычислять 10^20 позиций в течении: 10^20 / 10.400.590 = 9,6×10^12 часов = 4×10^11 дней.

Посмотрим, какой кусок кода является «узким горлышком». Для этой цели я использовал профилировщик OProfile:

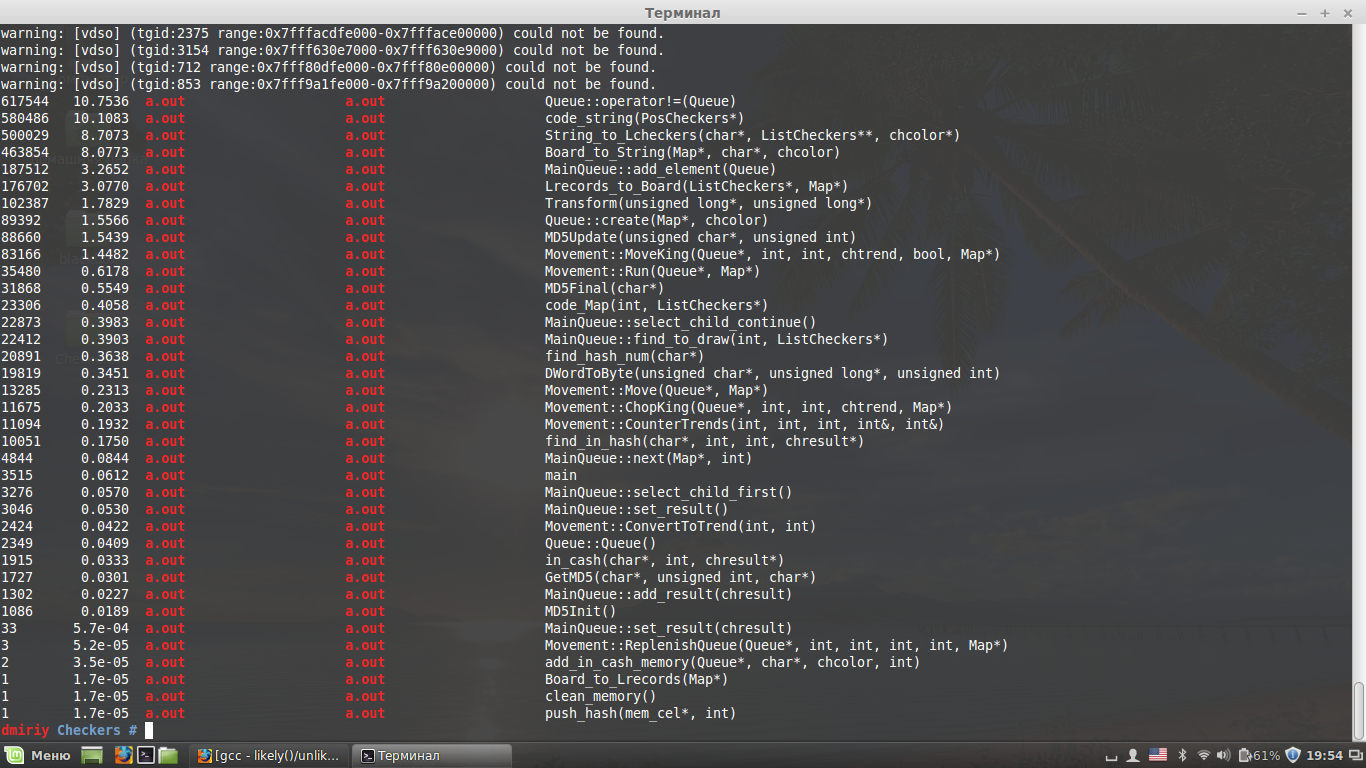
1.

Queue::operator!=(Queue)

Проверка различности элементов очереди. Вызывается при добавлении нового элемента в очередь для проверки троекратного повторения позиции. Проверка производится со всеми элементами, которые привели к текущей позиции.

Оптимизация: При изменении количества шашек на доске или их статуса, отметить. Для того чтобы с позициями, которые имеют другой набор фигур, не производить проверку.

2.

code_string(PosCheckers*)

Используется для преобразования элемента шашечной позиции в букву. Необходим для функции Board_to_String (Map*, char*, chcolor).

Оптимизация: Для начала уменьшить количество вызова функции Board_to_String (Map*, char*, chcolor)

3.

String_to_Lcheckers(stringMap, ListCheckers**, chcolor*)

4.

Board_to_String(Map*, char*, chcolor)

Вызываются достаточно часто. А значит необходимо уменьшить количество обращений к ним.
String_to_Lcheckers необходим для преобразования текста в коллекцию из данных о шашках.
Board_to_String необходим для перевода позиции в текст, который можно хранить в ОП.

Оптимизация: Так как для представления одной и той же позиции на доске мне необходимо работать с тремя структурами данных:

Lcheckers — список шашек на поле. Необходим для быстрого выбора шашки для просмотра возможности хода. Map или «Board» — массив [8][8]. Содержит в себе полную расстановку сил.
stringMap или «String» — строка для хранения данных. Значит необходимо уменьшить количество конвертаций из одного представления данных, в другой или попытаться уменьшить количество структур данных.

Магические bitBoard«ы

Неожиданно для себя я нашёл решение на habrahabr: Магические битборды и русские шашки. В котором автор статьи предлагает закодировать информацию о доске при помощи 4-ёх 32-битных слов.

Слова:

1) позиции всех фигур белого цвета
2) позиции всех фигур черного цвета
3) позиции шашек белого цвета
4) позиции шашек чёрного цвета

Причём позиции фигур нумеруются следующим образом:

Теперь для выяснения возможности сруба хотя бы одной шашкой достаточно позиции всех шашек передвинуть в соответствующем направлении:

bitboard_t try_left_up = ((((checkers & possible_left_up) << 1) & enemy) << 1) & empty;

Тем самым ускоряется поиск возможности, как сруба, так и простого хода. К своему большому сожалению, я так и не понял автора данной статьи, как он решил работать с дамкой. У меня на данный момент стоит не красивый for, который, конечно, в дальнейшем нужно исправить.

Тем самым можно заменить 3 структуры данных, описанных выше на одну:

typedef uint32_t bitboard_t;
bitboard_t bbMap[4];

Также, это изменение позволило не использовать md5 для нахождения номера в hash-таблице. Эта миссия была поручена данной формуле:

#define HASH_NUM 0xFFFFFF
hash_num = ((bbMap[0] ^ ~bbMap[1]) ^ ReverseBits(~bbMap[2] ^ bbMap[3])) & HASH_NUM;

Где ReverseBits — это разворот бит. Пример: было число 0×80E0, стало 0×0701.

Результат:

Запуск на 1 час позволил просмотреть 754.000.000 позиций, что, несомненно, лучше. Но этого всё ещё не достаточно для полного просчёта.

Считаю, что алгоритм проекта реализован. Поэтому, можно сделать упор на ускорении работы функций.

Ускорение работы функций

Начитавшись о likely/unlikely я решил проверить насколько проверить его «ускорение» кода. В общем говоря, likely/unlikely указывает какие инструкции следует загружать процессору во время выполнения оператора if. Либо те, которые находятся после then, либо после else. При неудачном выборе инструкций, например then, процессор простаивает, ожидая инструкций, указанных после else. Под Windows такая инструкция называется __assume.

Реализовав каждый if этим способом, я решил затестить:

__assume(selected == nullptr);
if (selected != nullptr)
{
return selected;
}

Результат:

К своему большому удивлению, код ускорился действительно на много. За первый час было просчитано 840 млн. позиций.

Реализовывать ассемблерные вставки я не решился. Код у меня становится сразу нечитаемым, а это является для меня важным аспектом. Так как перерывы в проекте у меня иногда достигали несколько месяцев.

Ограничитель количества просчитанных ходов в глубь

К сожалению, это можно назвать так: со временем, я действительно осознал, что просчитать все позиции пока невозможно. Поэтому я добавил ограничитель ходов с результирующей функцией:
шашка = +1 балл, дамка = +3 балла. Я осознаю, что такой подход не совсем верен, но в большинстве своём он будет выдавать валидные значения. Поэтому я решил остановиться на этом.

Результат:

Я вернулся к тому, с чего начал. С ограничителем количества просчитанных ходов моя программа на данный момент является программой для решений комбинационных задач. Но это не страшно, ограничитель можно отдалить.

Общий результат:

За первый час просчитывается ≈850 млн. позиций. Что делать дальше? Непонятно. Можно использовать CUDA, распараллелить вычисления… Но не думаю, что с помощью этого можно добиться просчёта хотя бы 50 ходов для каждого игрока на одном компьютере. Знать бы ещё сколько позиций перебрать придётся…

Нужно менять алгоритм… Как? Идей нет… Может использовать разрекламированные нейронные сети? Не думаю, что нейронная сеть оценит по достоинству потерю шашки в начале партии.

Пока что подожду грядущее время появление/удешевления более быстрых компьютеров. Авось, тогда уже появятся более продвинутые технологии в ускорении кода. А я пока пойду изучать нейронные сети, возможно я не прав и они будут во главе вычислительного алгоритма… Поживём-посмотрим.

Комментарии (1)

impwx

22 декабря 2016 в 14:21

0

↑

↓

Добро пожаловать в безжалостный мир алгоритмической сложности :)
При вашей скорости 10^20 комбинаций будут обсчитываться порядка 13 миллионов лет. Я бы не рассчитывал дожить до момента, когда это можно будет сделать в разумное время на машине, доступной простому обывателю. Судя по тому, что игра до сих пор не просчитана полностью, это даже на кластере невозможно сделать.
Разве что случится революция в виде квантовых вычислений, но до этого момента можно смело изучать нейронные сети.