[Из песочницы] Поиск похожих документов с MinHash + LHS
В этой публикации я расскажу о том, как можно находить похожие документы с помощью MinHash + Locality Sensitive Hashing. Описание LHS и Minhash в «Википедии» изобилует ужасающим количеством формул. На самом деле все довольно просто.1. Выделение признаков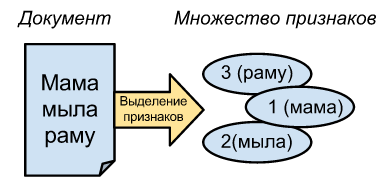
Под документом в этой статье я понимаю обычный текст, но в общем случае это может быть любым массивом байт. Штука в том, что для сравнения любого документа с помощью MinHash его необходимо сначала преобразовать в множество элементов.
Для текстов неплохо подойдет преобразование в множество ID слов. Скажем, «мама мыла раму» → [1, 2, 3], а «мама мыла» → [1, 2].
Похожесть этих множеств равна 2/3, где 2 — количество похожих элементов, а 3 — общее количество разных слов.
Также можно разбить эти тексты на N-граммы, например, «мама мыла раму» разбивается на триграммы «мам, ама, ма_, а_м, …», что даст похожесть 7/12.
2. Создание сигнатуры с MinHash
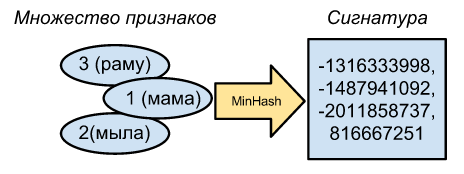Капитан очевидность говорит нам, что MinHash — это минимальный хэш из всех хэшей нашего множества. Скажем, если у нас есть хэшфункция, которая возвращает значение на входе, то множество ID слов [1, 2, 3] преобразуется в множество хэшей [1, 2, 3] где минимальный хэш равен 1, а минимальный хэш для [1, 2] очевидно тоже даст единицу. Вроде несложно.
Вероятность того, что минимальные хэши для двух множеств совпадут, весьма точно равна похожести этих двух множеств. Доказывать я это не хочу, т.к. у меня аллергия на формулы, но это очень важно.
Окей, имея один минхэш, мы особо много не сделаем, но уже понятно, что одинаковые множества дадут одинаковый минхэш, а для совершенно разных множеств и идеальной хэш-функции он гарантированно будет разным.
Для закрепления результата мы можем взять много разных хэш-функций и для каждой из них найти минхэш. Довольно просто можно получить много разных хэш-функций, сгенерировав много случайных, но различных чисел, и ксорить нашу первую хэшфункцию на эти числа. Скажем, сгенерируем совершенно случайные числа 7 и 8, что даст нам две дополнительные хэш-функции. Тогда минхэши для [1, 2, 3] будут 1, 4, 9, а для [1, 2] сигнатура будет равна 1, 5, 9. Как видно, первые и последние пары минхэшей совпадают, из чего очень грубо можно предположить, что похожесть исходных множеств равна 2/3. Понятно, что чем больше хешфункций, тем точнее можно определить похожесть исходных множеств.
3. Создание ключей с Locality Sensitive Hashing
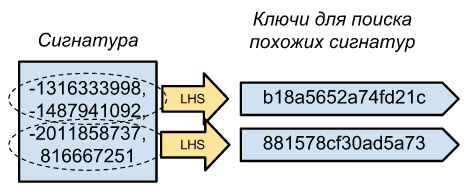Мы теперь можем определить, насколько похожи документы используя только их сигнатуры (N значений минхэшей), но что нужно писать в хранилище key-value для возможности выборки по всем более-менее похожим документам? Если использовать целые сигнатуры в качестве ключей, то мы сделаем выборку только по практически идентичным документам, т.к. вероятность того что N минхешей совпадет равна s^N где s — одинаковость документов.
Решение простое — допустим наши сигнатуры состоят из 100 чисел, мы можем разбить ее на несколько частей (скажем, 10 частей по 10 чисел), после чего все эти части сделать ключами целой сигнатуры.
Вот и все, теперь для определения того что у нас в базе уже есть похожий документ. Нужно получить его сигнатуру из 100 минхешей, разбить на десять ключей и для всех соответствующих им полных сигнатур вычислить ее похожесть (количество совпадающих минхешей).
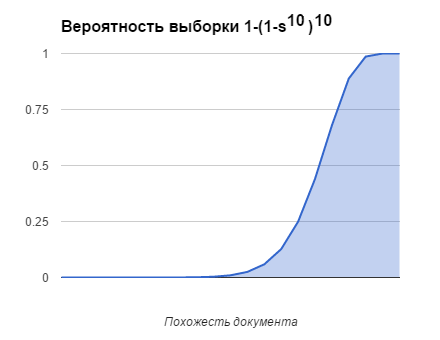
Для десяти ключей с десятью элементами в каждом вероятность выборки документа в зависимости от похожести документа будет такая:
