[Из песочницы] Персистентное декартово дерево по неявному ключу
Осторожно, персистентность Сегодня достаточно необычный день, не правда ли? Как часто на Хабре появляются статьи про персистентные структуры данных? И именно сегодня я желаю вам рассказать про незаслуженно забытую персистентную дерамиду по неявному ключу. Итак, начнем.1. Что вообще автор подразумевает под персистентностью? Согласно источнику знаний, персистентная структура данных — это такая структура данных, которая хранит информацию о всех своих предыдущих версиях, когда происходили операции ее изменения.Есть несколько вариантов того, как можно сделать структуру данных персистентной. В данном случае мы будем создавать полностью персистентную структуру данных за счет копирования только тех вершин, в которых что-либо поменялось. Таким образом, нам не надо как-то менять структуру обычной дерамиды или полностью копировать все дерево при каком-то изменении. Хорошо? Конечно!2. Как же это сделать? Рассмотрим обычную структуру дерамиды по неявному ключу. Для того, чтобы не быть голословными, будем считать сумму на отрезке. struct PersistentTreap { int size; long long sum, key; PersistentTreap *left, *right; //сюда будут добавлены еще переменные PersistentTreap () { left = NULL; right = NULL; key = sum = 0; size = 0; } PersistentTreap (int x) { left = right = NULL; sum = key = x; size = 1; link = 0; } //И это тоже еще не все };
typedef PersistentTreap* PtrPersistentTreap;
int getSize (PtrPersistentTreap root) { if (! root) return 0; return root→size; }
long long getSum (PtrPersistentTreap root) { if (! root) return 0; return root→sum; }
void addLink (PtrPersistentTreap root) { if (! root) return; root→link++; }
void update (PtrPersistentTreap root)
{
if (! root)
return;
root→size = 1 + getSize (root→left) + getSize (root→right);
root→sum = root→key + getSum (root→left) + getSum (root→right);
}
Как вы видите, это довольно тривиальная часть кода, которая известна всем, кто хоть раз писал дерамиду по неявному ключу. Теперь перейдем к самому интересному: как сделать так, чтобы операции split, merge и push (как вариант) не меняли необратимо структуру дерева? Рассмотри несколько картинок, которые помогут нам в этом разобраться.Исходное декартово дерево до операции split. (в вершинах указаны числа, которые им соответствуют в массиве). То есть это аналогично массиву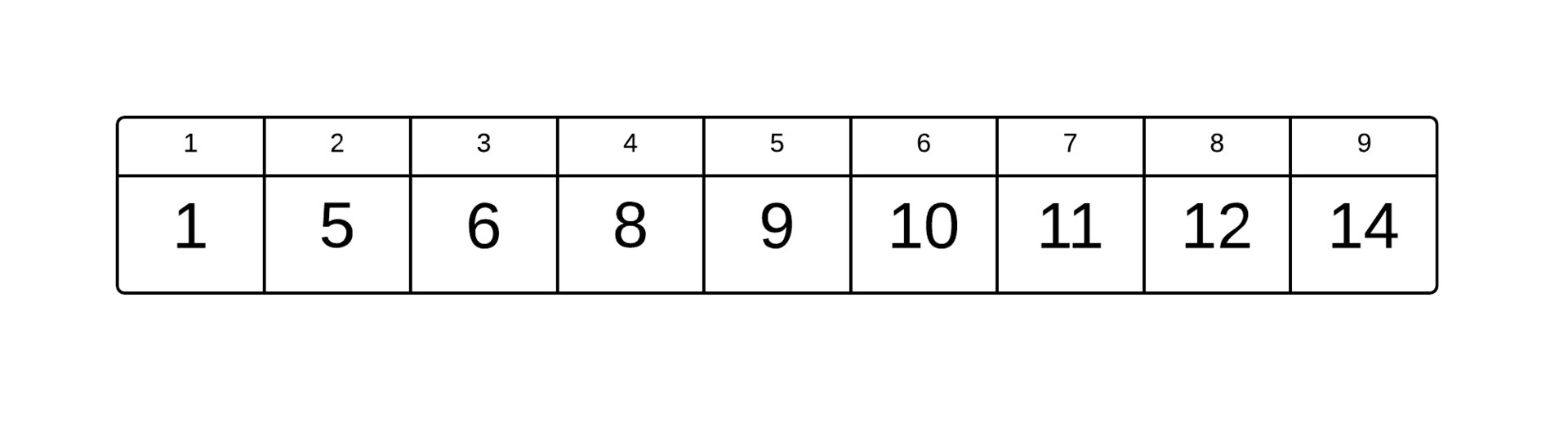 
.
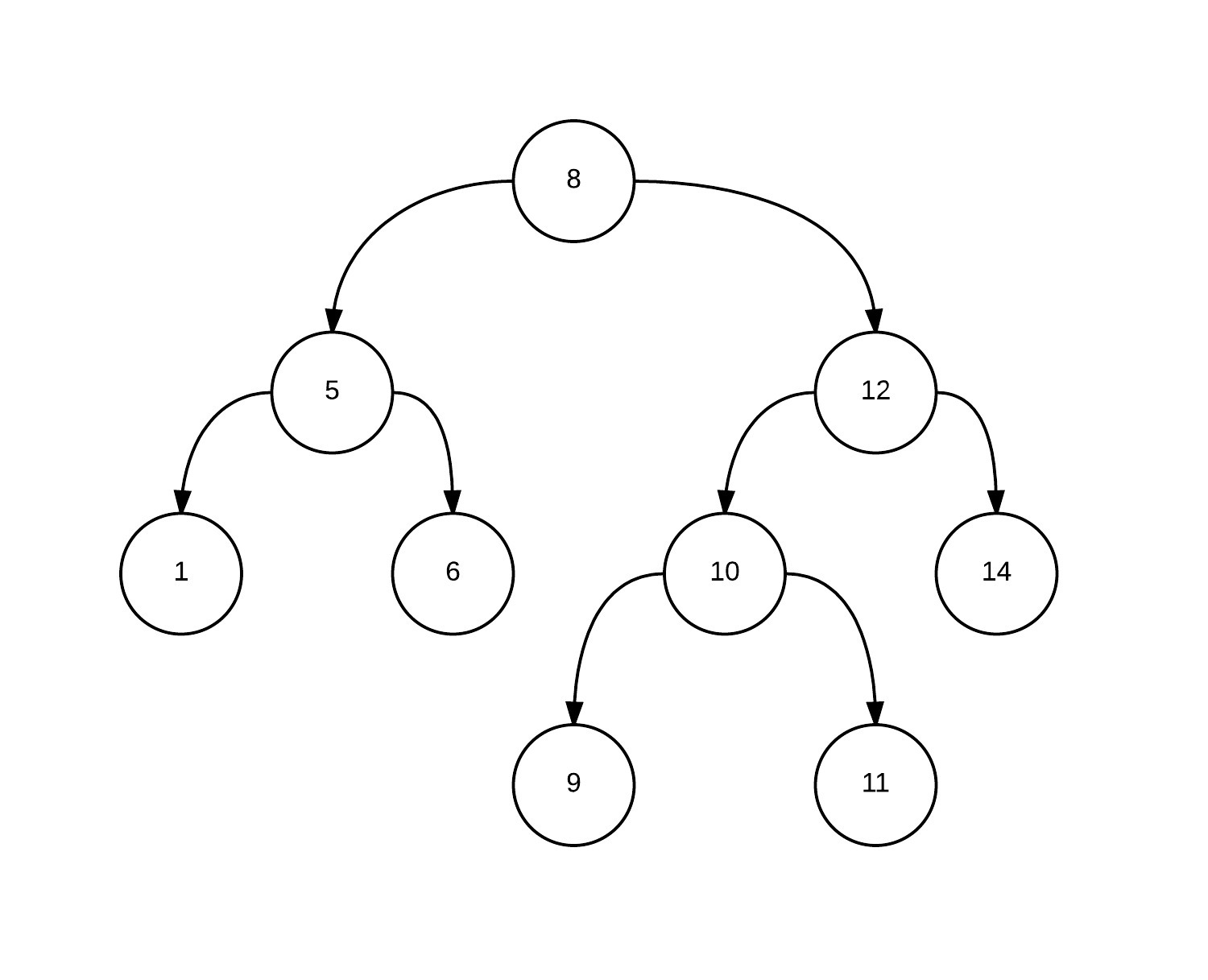После персистентной операции split, в которой мы запросили в правом дерево 5 элементов, мы получаем следующий лес. Синим обозначены вершины исходной дерамиды, зеленым — созданные новые вершины. Пунктирными стрелками — связи между новыми вершинами.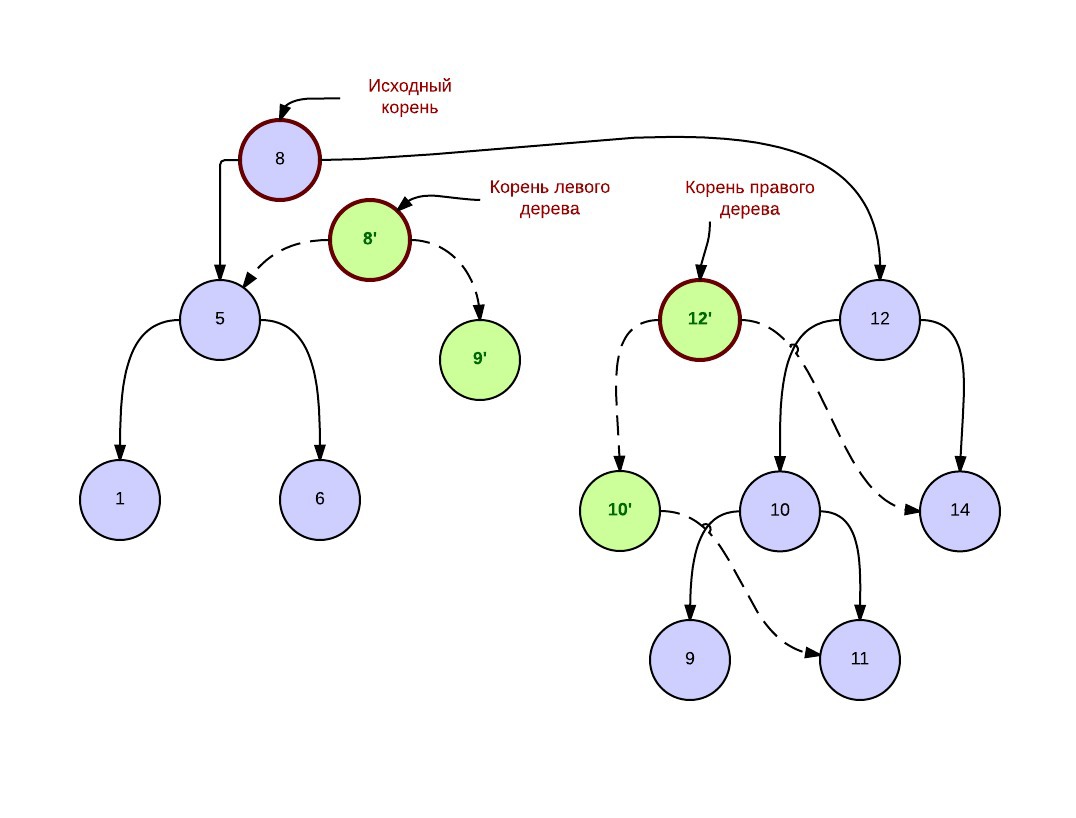
Итак, при каждом рекурсивном вызове операции split мы не имеем права каким-либо образом модифицировать уже имеющиеся дерево, нам необходимо создать новую вершину, которая является точно копией данной и проводить все операции изменения только с ней. Буквально это мы и напишем. Для этого мы первым долгом создадим конструктор копирования:
PersistentTreap (PersistentTreap* cur)
{
if (! cur)
{
return;
}
left = cur→left;
right = cur→right;
sum = cur→sum;
key = cur→key;
size = cur→size;
}
Все, теперь можно писать персистентный вариант операции split. Ее единственное различие с обычной только в том, что мы просто копируем корень, который требуется изменить, и дальше продолжаем выполнять свою обычную работу.
void Split (PtrPersistentTreap root, PtrPersistentTreap &L, PtrPersistentTreap &R, int size)
{
if (! root)
{
L = R = NULL;
return;
}
PtrPersistentTreap cur = new PersistentTreap (root);
if (getSize (cur→left) + 1 <= size)
{
split(cur->right, cur→right, R, size — getSize (cur→left) — 1);
L = cur;
}
else
{
split (cur→left, L, cur→left, size);
R = cur;
}
update (L);
update®;
}
Прекрасно, треть все работы выполнена. Теперь необходимо разобраться с персистентной операцией merge. Рассмотри две дерамиды, которые были получены каким-то образом (опять же, считаем, что все получено из исходного массива). Для корректной работы операции merge, присвоим им приоритеты так, чтобы в корне был максимальный (выделены красным цветом в скобочках). Позже будет показано, что они на самом деле не нужны для правильной работы алгоритма.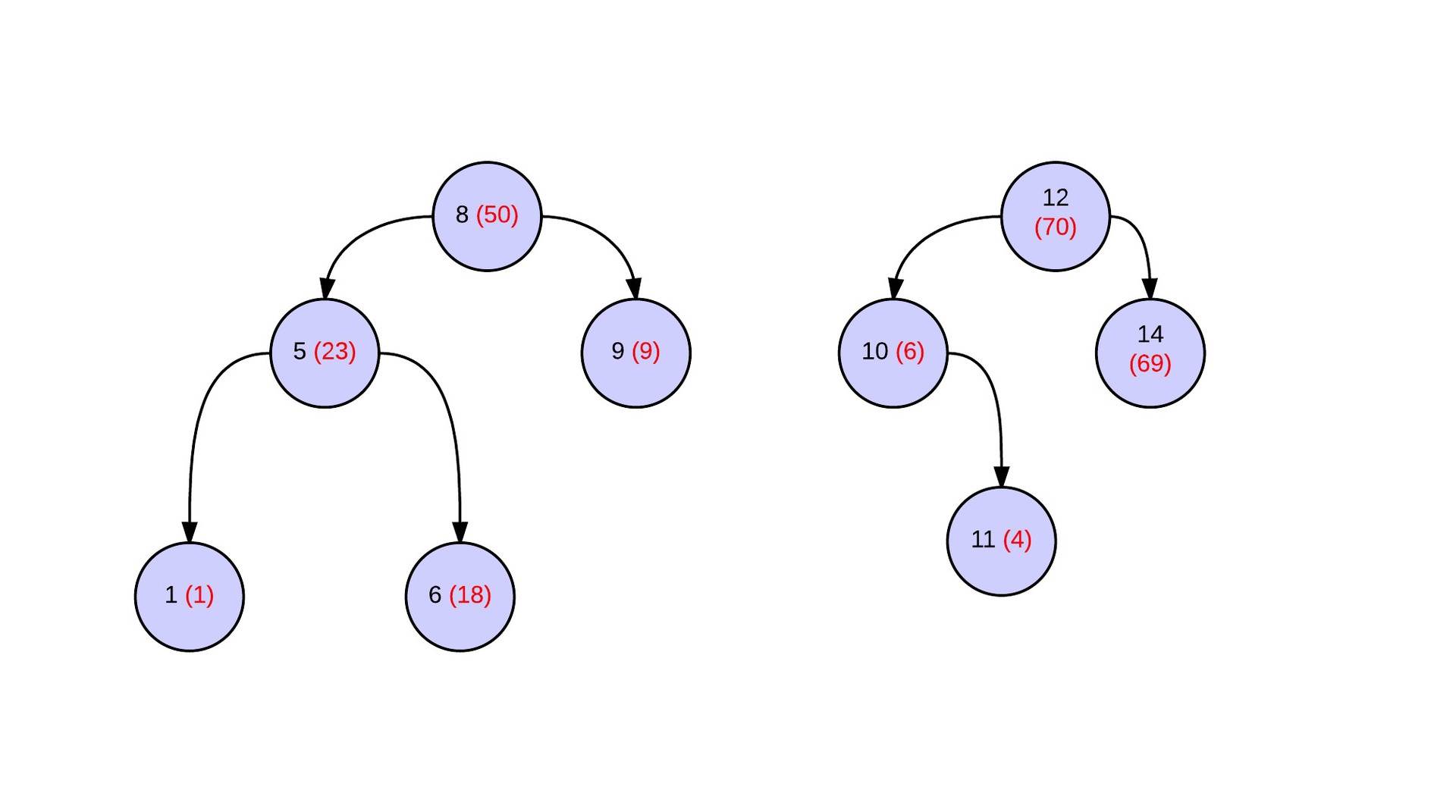
Результатом операции merge является дерамида, в которой выполняются свойства кучи для приоритетов вершин. Ниже приведена картинка дерева после операции merge. Синим обозначены вершины исходной дерамиды, зеленым — созданные новые вершины. Пунктирными стрелками — связи между новыми вершинами.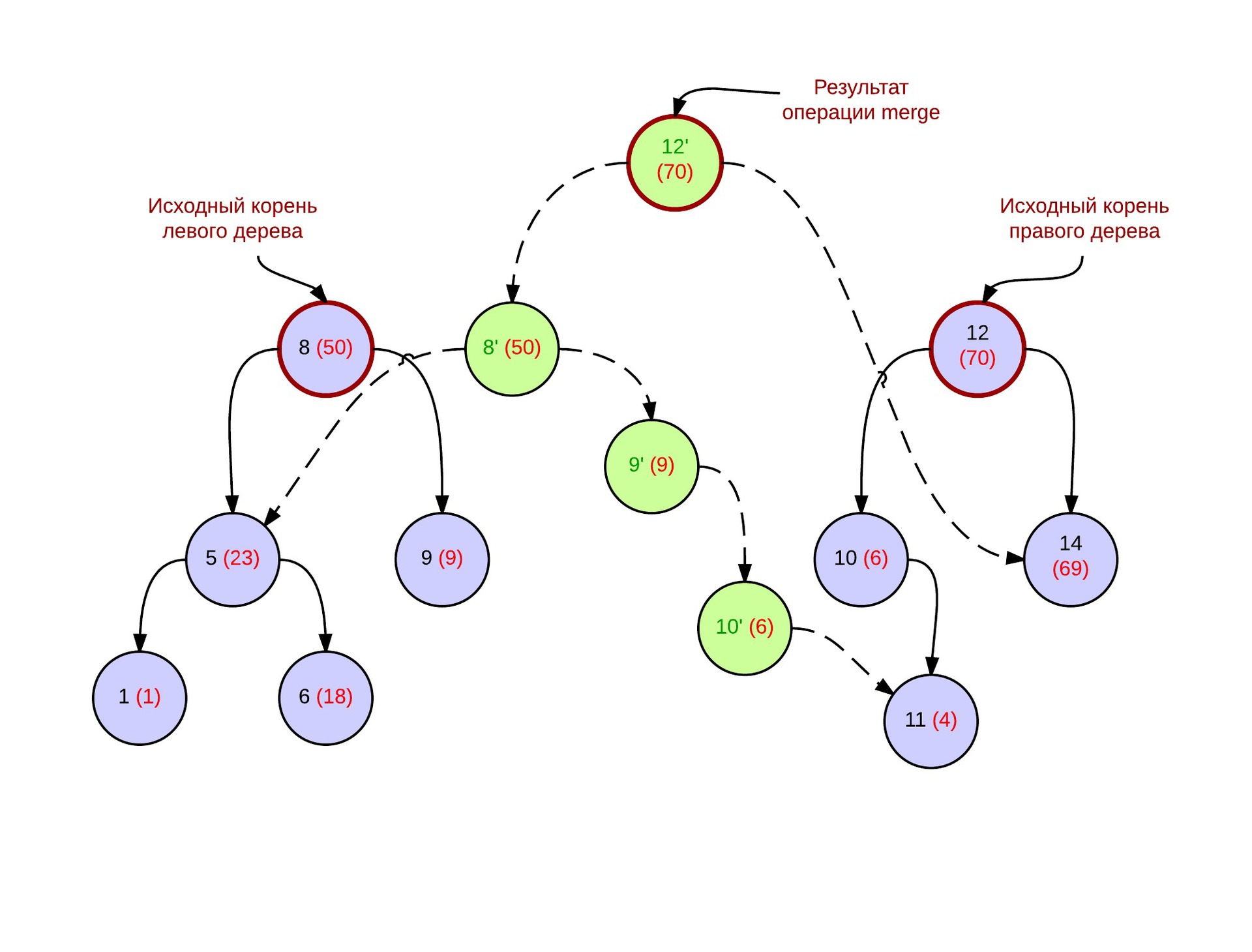
В нашей реализации мы будем требовать, чтобы merge возвращал указатель на новую вершину дерева. Таким образом на каждом вызове мы копируем вершину, которая станет корнем, и меняем у нее указатель на одного из ее сыновей. На какого — зависит от того, левое или правое дерево это было.
PtrPersistentTreap Merge (PtrPersistentTreap L, PtrPersistentTreap R)
{
PtrPersistentTreap ptrNode = NULL;
if (! L || ! R)
{
ptrNode = new PersistentTreap ((! L? R: L));
return ptrNode;
}
if (L→prior > R→prior)
{
ptrNode = new PersistentTreap (L);
ptrNode→right = Merge (L→right, R);
update (ptrNode);
return ptrNode;
}
else
{
ptrNode = new PersistentTreap®;
ptrNode→left = Merge (L, R→left);
return ptrNode;
}
}
Однако было обещано, что в вершинах совершенно не нужно хранить целое поле prior, сейчас я расскажу вам, как можно от него избавиться (исключительно полезно для персистентной реализации). Действительно, при совпадении приоритетов дерево может выродиться в обыкновенный бамбук, что сводит его пользу сразу на нет. Выставлять же при каждом обращении к вершине новый приоритет — дорогое удовольствие, не факт, что он точно не совпадет с каким-либо другим, да и не факт, что сохранится структура дерева. Оказывается есть простое и элегантное решение.Каждая вершина дерамиды хранит в размер дерева, которое она представляет. Значит с этой величиной можно попытаться связать приоритет вершины на то, чтобы стать корнем. Достаточно логично сделать так, чтобы приоритет вершины, у которой больший размер дерева, был больше. Докажем теперь, что в таком случае каждая вершина имеет одинаковую вероятность стать корнем дерева. Сделаем это по индукции. Пусть мы хотим выбрать корень из двух вершин. Очевидно, что вероятности стать корнем для них равны. Теперь рассмотрим случай, когда у нас в левом дереве всего L вершин, а в правом — R. Тогда, согласно алгоритму, вершина из левого дерева может стать корнем с вероятностью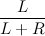 
. Но каждая вершина вершина дерева L могла стать корнем с вероятность 
. А значит каждая вершина дерева L может стать корнем с вероятностью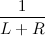 
. Аналогично рассматривается случай для правого дерева. Все, переход доказан, так как вероятности для всех вершин одинаковые.Таким образом, в операции merge вместо
if (L→prior > R→prior) можно написать int l = getSize (L), r = getSize®, rang = rand () % (l + r); if (rang > r) и ничего не изменится.3. Добавления подсчета ссылок на вершину. Ура, основная часть персистентной структуры данных написана. Следующие изменения, которые нужно внести — это реализация подсчета ссылок. Для этого в стоит добавить поле link, отвечающие за хранения количества вершин, которые ссылаются на данную. Логично предположить, что если данное поле не пусто, то мы ни в коем случае не можем просто так удалить текущую вершину, ибо это повлияет как-то на оставшиеся версии дерева. И да, при удалении какой-то вершины мы также уменьшаем link в ее детях и вызываем рекурсивное удаление, если это требует.Операции split и merge с этим добавлением и дополнение самой структуры дерева struct PersistentTreap { short link; int size; long long sum, key; PersistentTreap *left, *right; PersistentTreap () { left = NULL; right = NULL; key = sum = 0; size = 0; link = 0; } PersistentTreap (PersistentTreap* cur) { if (! cur) { return; } left = cur→left; right = cur→right; sum = cur→sum; key = cur→key; size = cur→size; link = 0; } PersistentTreap (int x) { left = right = NULL; sum = key = x; size = 1; link = 0; } void del () { link--; if (link <= 0) { if (left != NULL) left->del (); if (right!= NULL) right→del (); delete this; } } };
void addLink (PtrPersistentTreap root) { if (! root) return; root→link++; }
void DelNode (PtrPersistentTreap root) { if (! root) return; root→del (); }
void Split (PtrPersistentTreap root, PtrPersistentTreap &L, PtrPersistentTreap &R, int size) { if (! root) { L = R = NULL; return; } PtrPersistentTreap cur = new PersistentTreap (root); if (getSize (cur→left) + 1 <= size) { Split(cur->right, cur→right, R, size — getSize (cur→left) — 1); addLink (cur→left); addLink (cur→right); L = cur; } else { Split (cur→left, L, cur→left, size); addLink (cur→left); addLink (cur→right); R = cur; } update (L); update®; }
PtrPersistentTreap Merge (PtrPersistentTreap L, PtrPersistentTreap R) { PtrPersistentTreap ptrNode = NULL; if (! L || ! R) { ptrNode = new PersistentTreap ((! L? R: L)); addLink (ptrNode→left); addLink (ptrNode→right); return ptrNode; } int l = getSize (L), r = getSize®, rang = rand () % (l + r); if (rang > r) { ptrNode = new PersistentTreap (L); ptrNode→right = Merge (ptrNode→right, R); addLink (ptrNode→left); addLink (ptrNode→right); update (ptrNode); return ptrNode; } else { ptrNode = new PersistentTreap®; ptrNode→left = Merge (L, ptrNode→left); addLink (ptrNode→left); addLink (ptrNode→right); update (ptrNode); return ptrNode; } } Теперь мы можем с полным правом утверждать, что окончательно написали персистентную дерамиду по неявному ключу. Для чего же оно может нам понадобиться? Оно умеет делать абсолютно такие же операции, как и обычная дерамида по неявному ключу, но в отличие от нее, теперь мы можем копировать куски массива, вставлять копии кусков массива обратно в массив, не опасаясь совпадения приоритетов или возрастания затрат времени связи с полным копированием дерамиды. Пример использования персистентной дерамиды.
