[Из песочницы] Парадокс дней рождений на данных ВКонтакте
Привет!
Я решил проверить парадокс дней рождений на данных, которые доступны из ВК.
Что такое парадокс дней рождений?
Попробуйте ответить на вопрос: Какое количество людей в комнате необходимо, чтобы у двух людей были одинаковые дни рождения с вероятностью 0.5? (дата и месяц). Парадокс дней рождений отвечает на этот вопрос.
Для того, чтобы решить задачу стоит выделить несколько предпосылок:
- В модели не будет 29 февраля => в модели 365 дней в году
- Каждый из 365 дней равновероятен.
Конечно, это не совсем реалистично, что дни рождения равновероятны — есть сезонные эффекты, влияющие на даты рождения детей, думаю вы сами можете догадаться какие…
Большинство людей интуитивно отвечают на вопрос задачи: 180. Выглядит логично, 180 человек необходимо для того, чтобы иметь вероятность 0.5 одинаковых дней рождений (всего же 365 дней). Примерна такая интуиция у всех, кто никогда не слышал про парадокс дней рождений. Правильный ответ на самом деле сильно меньше 180, и даже 150, и даже 100: 23.
Необходим как минимум 1 совпадающий день рождения — поэтому я могу найти вероятность, отсутствия совпадающих дней рождений:
$$display$$P («различные \space ДР») = \frac {365×364 * 363 * … * (365 — k + 1)} {365 ^ k} = \frac {365!} {365^k * (365 — k)!}$$display$$
.
Идея такая: я беру первого человека и запоминаю его день рождения, далее второго и вычисляю вероятность, что его день рождения не совпадает с днем рождения первого; далее третьего и его вычисляю вероятность, что его день рождение не совпадет с днями рождения первого и второго.
Решая уравнение, получается, что необходимо 23 человека и вероятность совпадающих дней рождений будет 0.5073, при 100 людях, вероятность равна 0.9999.
Посмотрим парадокс на данных ВК?
В теории у нас при 23 людях вероятность совпадающих дней рождений 0.5073, при 50 людях 0.97, а при 100 0.99. Проверим это через VK API.
1. Выбираю большое сообщество в ВК. Я решил взять группу MDK во Вконтакте…
В начале я создаю csv файл с колонками, которые мне необходимы.
with open('vk_data.csv', 'w') as new_file:
# csv
fieldnames = ['id', 'bdate', 'bmonth', 'byear', 'dandm']
csv_writer = csv.DictWriter(new_file, fieldnames=fieldnames, delimiter=',')
csv_writer.writeheader()
newDict = dict()
Логинюсь в ВК через API и задаю необходимый мне паблик
vk_session = vk_api.VkApi('username', 'password')
vk_session.auth()
vk = vk_session.get_api()
vk_group = vk.groups.getMembers(group_id = 'mudakoff', fields = 'bdate')
Начинаем парсить ВКонтакте, их API позволяет запарсить только 1000 юзеров, поэтому создаю цикл.
for i in range(0, 20):
vk_group = vk.groups.getMembers(group_id = 'mudakoff', offset = 1000 * i, fields = 'bdate')
for k in range(0, 1000):
try:
new_file.write(str(vk_group['items'][k]["id"]) + ',' + str(vk_group['items'][k]["bdate"]).replace('.', ','))
new_file.write('\n')
except:
pass
В теории мы предполагали, что дни рождения равновероятны, а что происходит на практике? Построю гистограмму дней рождений.
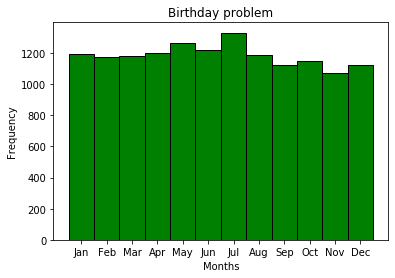
Дни рождения по месяцам не являются равновероятнотными событиями, что в целом достаточно логично — это всего лишь предпосылка для решения проблемы дней рождений. Очевидно, что будут наблюдаться различные сезонные являения, для различных локаций. Почему-то июль наиболее популярный месяц для дня рождения подписчиков МДК.
Эмпирически оценю вероятность того, что в группе из 50 произвольных людей найдутся хотя бы двое с одинаковым днём рождения. Для этого я написал цикл, в ходе которого из таблички происходит подвыборка из 50 строк. Для этих 50 строк внутри условия я проверил совпадение дней рождений. Если совпало, то я запомнил это в переменную счётчик, которую я впоследствии, чтобы получить вероятность, поделю на длину цикла.
fifty = df["dandm"].sample(n = 50)
for i in range(0, 1000):
fifty = df["dandm"].sample(n = 50)
for j in fifty.duplicated():
if j == True:
counter = counter + 1
break
print('Вероятность:', counter / 1000)
Вероятность получается в районе 0.97, что совпадает с теоретическими данными.
Вывод
Интересно было посмотреть, как теория соотносится с эмпирикой и в данном случае данные подтверждают теорию. Стоит отметить, что результат репрезентативен, так как выборка достаточно большая — 20000 человек.
Ресурсы
- Harvard University. Birthday Problem, Properties of Probability | Statistics 110. URL: www.youtube.com/watch? v=LZ5Wergp_PA&t=150s. Accessed: 08.07.2020
- Birthday Problem. URL: en.wikipedia.org/wiki/Birthday_problem. Accessed: 08.07.2020>
