[Из песочницы] Оптимизация портфеля облигаций с применением библиотеки ALGLIB
В статье пойдет речь об опыте разработки программы для составления эффективного портфеля облигаций с точки зрения минимизации его дюрации. Возможно, я не буду оригинален и для всех, кто инвестирует в облигации вопросы определения оптимальных весов давно решены, но все же, надеюсь, описанный подход и приведенный программный код будут кому-то полезны.
Статья, ввиду наличия в ней не малого объема математики, кому-то может показаться усложненной. Но если уж Вы решили заняться инвестициями, то нужно быть готовым к тому, что в финансовой реальности часто встречается математика и еще значительно сложнее.
Исходные коды программы и пример портфеля для оптимизации выложены на GitHub.
Итак, имеем задачу сформировать эффективный портфель облигаций.
С точки зрения минимизации несистемных рисков (ради чего и диверсифицируется портфель) выбор бумаг осуществлялся рассмотрением параметров конкретного выпуска, эмитента (если не ограничиваться ОФЗ), поведением бумаги и т.д. (подходы к такому анализу достаточно индивидуальны для каждого инвестора и в данной статье не рассматриваются).
Отобрав, несколько бумаг, наиболее предпочтительных для инвестирования, возникает естественный вопрос: сколько штук облигаций каждого выпуска нужно купить? Это и есть задача оптимизации портфеля так, чтобы риски портфеля были минимальны.
В качестве оптимизируемого параметра естественно рассмотреть дюрацию. Таким образом, задача сводится к тому, чтобы определить веса бумаг в портфеле, такие, при которых дюрация портфеля была бы минимальной при некоторой фиксированной доходности портфеля. Здесь необходимо сделать несколько оговорок:
- Дюрация портфеля облигаций определяется входящими в его состав бумагами. Эти дюрации известны (они в открытом доступе). Дюрация портфеля не равна максимальной дюрации, входящих в него бумаг (есть такое заблуждение). Зависимость между дюрациями отдельных бумаг и дюрацией всего портфеля не линейна, т.е. не равна средневзвешенной дюрации составляющих его облигаций (Для того, чтобы убедиться в этом достаточно рассмотреть формулу дюрации (см. ниже (1)) и попытаться вычислить средневзвешенную дюрацию условного портфеля, состоящего, например, из двух бумаг. Подставив в такое выражение формулу для дюрации каждой бумаги, на выходе получим не формулу для дюрации портфеля, а некий «бред», с двумя ставками дисконтирования и несогласованными денежными потоками в качестве весов).
- В отличие от дюрации, доходность портфеля, зависит от доходностей, входящих в него инструментов линейно. Т.е. разместив деньги в несколько инструментов с фиксированной доходностью, мы получим доходность, прямо пропорциональную объемам вложений в каждый инструмент (причем это работает и для сложной ставки, а не только для простой). Убедиться в этом еще проще.
- В качестве ставки доходности облигаций используется доходность к погашению (YTM). Она обычно и применяется для расчета дюрации. Однако, доходность к погашению всего портфеля здесь довольно условна, т.к. срок до погашения у всех бумаг разный. При формировании портфеля эту особенность необходимо учитывать в том смысле, что портфель должен пересматриваться, не реже чем инструменты, из которых он составлен, выходят из оборота.
Итак, первой задачей является корректное вычисление дюрации самого портфеля. Непосредственным способом сделать это является: определение всех платежей по портфелю, вычисление доходности к погашению, дисконтирование платежей, умножение полученных величин на сроки этих платежей и суммирование. Для того, чтобы это проделать нужно объединить календари платежей всех инструментов в единый календарь платежей по всему портфелю, составить выражение для расчета доходности к погашению, вычислить её, дисконтировать по ней каждый платеж, умножить на его срок выплаты, сложить…. В общем, кошмар. Даже для двух бумаг проделать такое — очень трудоемкая задача, не говоря уж о том, чтобы в дальнейшем портфель регулярно пересчитывать. Такой путь нам не подходит.
Следовательно, необходимо искать возможность определить дюрацию портфеля иным, более быстрым способом. Приемлемым вариантом будет такой, который позволяет определить дюрацию портфеля по известным дюрациям инструментов. Исследования формулы дюрации показали, что такой путь имеется и здесь я бы хотел привести его подробно (если кому-то математические детали вычислений не интересны, можно смело пропустить несколько абзацев с формулами и перейти сразу к рассмотрению примера).
Дюрация долгового инструмента определяется следующим образом:
$$display$$ \begin{equation} D = \frac{\sum_{i}PV_i\cdot t_i}{\sum_{i}PV_i} ~~~~~~~~~~~~~(1) \end{equation} $$display$$
где:
- ti — момент времени i-го платежа;
- $inline$\begin{equation} PV_i = \frac{CF_i}{(1+r)^{t_i}} \end{equation}$inline$ — i-ый дисконтированный платеж;
- CFi — i-ый платеж;
- r — ставка дисконтирования.
Введем коэффициент дисконтирования k=(1+r) и будем рассматривать сумму дисконтированных платежей P как функцию от k:
$$display$$\begin{equation} P (k) = \sum_{i}PV_i = \sum_{i}{\frac{CF_i}{k^{t_i}}} ~~~~~~~~~~~~~(2) \end{equation}$$display$$
Дифференцируя P по k получаем
$$display$$\begin{equation} P'(k) = -\sum_{i}{t_i\frac{CF_i}{k^{t_i+1}}} = -\frac{1}{k}\sum_{i}{t_i\frac{CF_i}{k^{t_i}}} ~~~~~~~~~~~~~(3) \end{equation}$$display$$
С учетом последнего, выражение для дюрации облигации приобретает вид
$$display$$ \begin{equation} D = -k\frac{P'(k)}{P (k)} ~~~~~~~~~~~~~(4) \end{equation} $$display$$
При этом напомним, что в качестве ставки дисконтирования r в случае с облигацией применяется доходность к погашению (YTM).
Полученное выражение справедливо для одной облигации, но нас интересует портфель облигаций. Перейдем к определению дюрации портфеля.
Введем следующие обозначения:
- Pi — цена i-ой облигации;
- zi — количество бумаг i-ой облигации в портфеле;
- ki — коэффициент дисконтирования i-ой облигации в портфеле;
- $inline$\begin{equation} P_p = \sum_{i}{z_iP_i} \end{equation}$inline$ — цена портфеля;
- $inline$\begin{equation} w_i = \frac{z_iP_i}{\sum_{i}z_iP_i} = \frac{z_iP_i}{P_p} \end{equation}$inline$ — вес i-ой облигации в портфеле; очевидно требование $inline$\begin{equation} \sum_{i}w_i = 1 \end{equation}$inline$;
- $inline$\begin{equation} k_p = \sum_{i}w_ik_i \end{equation}$inline$ — коэффициент дисконтирования портфеля;
В силу линейности дифференцирования справедливо следующее:
$$display$$ \begin{equation} P'_p (k) = \left (\sum_{i}z_iP_i (k)\right)' = \sum_{i}z_iP'_i (k) ~~~~~~~~~~~~~(5) \end{equation} $$display$$
Таким образом, с учетом (4) и (5), дюрация портфеля может быть выражена как
$$display$$ \begin{equation} D_p = -k_p\frac{P'_p}{P_p} = -\sum_{i}w_ik_i\left (\frac{\sum_{j}z_jP'_j}{\sum_{j}z_jP_j}\right) ~~~~~~~~~~~~~(6) \end{equation} $$display$$
Из (4) однозначно следует $inline$\begin{equation} P'_j = -\frac{D_jP_j}{k_j} \end{equation}$inline$.
Подставляя данное выражение в (6) приходим к следующей формуле для дюрации портфеля:
$$display$$ \begin{equation} D_p = \sum_{i}w_ik_i\left (\frac{\sum_{j}\frac{D_j}{k_j}z_jP_j}{\sum_{j}z_jP_j}\right) = \left (\sum_{i}w_ik_i\right)\left (\sum_{j}w_j\frac{D_j}{k_j}\right) ~~~~~~~~~~~~~(7) \end{equation} $$display$$
В условиях, когда дюрация и доходность к погашению каждого инструмента известны (а мы, напомню, находимся именно в таких условиях) выражение (7) и есть искомая формула для определения дюрации портфеля на основе дюрации входящих в него облигаций. Она только с виду кажется сложной, но на самом деле она уже готова к применению на практике с помощью простейших функций MS Excel, что мы сейчас и проделаем на примере.
Пример
Для расчета дюрации портфеля по формуле (7) нам необходимы исходные данные, включающие собственно набор бумаг, входящих в портфель, их дюраций и доходностей к погашению. Как было сказано выше, данная информация имеется в открытом доступе, например, на сайте rusbonds.ru в разделе анализ облигаций. Исходные данные можно скачать в формате Excel.
В качестве примера рассмотрим портфель бумаг, состоящий из 9 облигаций. Исходная таблица с данными, скачанная с rusbonds, имеет следующий вид.
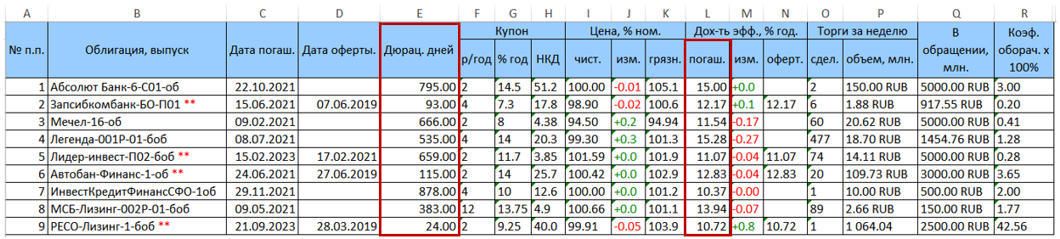
Красным выделены две интересующие нас колонки с дюрацией (колонка Е) и доходностью к погашению (колонка L = YTM).
Зададим веса w облигациям в данном портфеле (пока произвольным образом, но так, чтобы их сумма равнялась единице) и рассчитаем k = (1 + YTM/100) и D/k = («колонка Е»/k). Преобразованная таблица (без лишних колонок) будет иметь вид
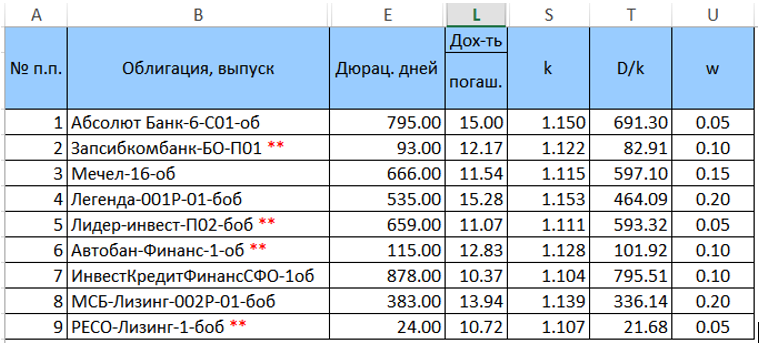
Далее рассчитаем произведения $inline$\begin{equation}w_j\frac{D_j}{k_j}\end{equation}$inline$ и $inline$\begin{equation}w_ik_i\end{equation}$inline$ и просуммируем их, а полученные суммы умножим одну на другую. Результат этого умножения и составит искомую дюрацию при заданном распределении весов.
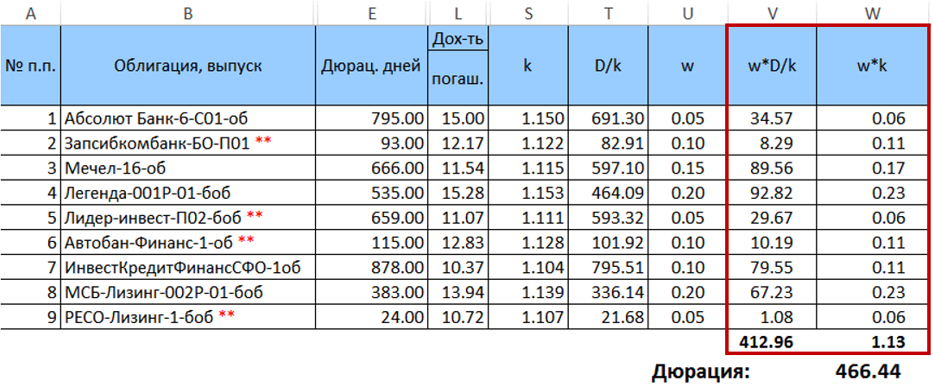
Итак, искомая дюрация портфеля равна 466,44 дня. Важно отметить, что в данном конкретном случае рассчитанная по формуле (7) дюрация очень незначительно отличается от средневзвешенной дюрации, рассчитанной с теми же весами (отклонение <0,5 дня). Однако эта разница увеличивается при увеличении разброса весов. Также она будет возрастать и при увеличении разброса дюраций бумаг.
После того, как нами получена формула для расчёта дюрации портфеля, следующим шагом является определение таких весов бумаг, чтобы при некоторой заданной доходности расчетная дюрация портфеля была бы минимальна. Переходим к следующей части — оптимизации портфеля.
Выражение (7) является квадратичной формой, с матрицей
$$display$$\begin{equation} A = \left\{ k_i\frac{D_j}{k_j}\right\} = \begin{pmatrix} D_1 & \ldots & k_1\frac{D_n}{k_n}\\ \vdots & D_j & \vdots\\ k_n\frac{D_1}{k_1} & \ldots & D_n \end{pmatrix} \end{equation}$$display$$
Соответственно, в матричной форме выражение для дюрации портфеля (7) можно записать так:
$$display$$\begin{equation} D_p = w^TAw ~~~~~~~~~~~~~(8) \end{equation}$$display$$
где w — вектор-столбец весов облигаций в портфеле. Как было сказано выше, сумма элементов вектора w должна быть равна единице. С другой стороны, выражение $inline$k_p = \sum_{i} w_i k_i$inline$ (которое, по сути, является простым скалярным произведением (w, k), где k — вектор коэффициентов дисконтирования облигаций) должно равняться целевой ставке дисконтирования портфеля, а значит задана и целевая доходность портфеля.
Таким образом, задача оптимизации портфеля облигаций сводится к минимизации квадратичной функции (8) с линейными ограничениями.
Классическим способом нахождения условного экстремума функции нескольких переменных является метод множителей Лагранжа. Однако здесь данный метод не применим хотя бы потому, что матрица A вырождена по построению (но не только в силу этого; подробности анализа применимости метода Лагранжа здесь опускаем, чтобы не перегружать статью избыточным математическим контентом).
Невозможность применить легкий и доступный аналитический метод приводит к необходимости использования численных методов. Задача оптимизации квадратичной функции хорошо известна и имеет несколько давно разработанных эффективных алгоритмов, реализованных в общедоступных библиотеках.
Для решения конкретно этой задачи применялась библиотека ALGLIB и реализованные в ней алгоритмы квадратичной оптимизации — QP-Solvers, входящие в пакет minqp.
Задача квадратичной оптимизации в общем виде выглядит следующим образом:
Требуется найти n-мерный вектор w, минимизирующий функцию
$$display$$\begin{equation} F = \frac{1}{2} w^T Qw+b^T w ~~~~~~~~~~~~~(9) \end{equation}$$display$$
С заданными ограничениями
1) l ≤ w ≤ u;
2) Cw * d;
где w, l, u, d, b — n-мерные действительнозначные векторы, Q — симметричная матрица квадратичной части, а знак * означает любое из отношений ≥=≤.
Как видно из (8) линейная часть bTw в нашей целевой функции равна нулю. Однако матрица А не является симметричной, что, впрочем, не мешает привести её к симметричному виду, не изменяя самой функции. Для этого достаточно положить вместо A выражение $inline$\begin{equation}\frac{A^T+A}{2}\end{equation}$inline$.Так как в формулу (9) входит коэффициент $inline$\frac{1}{2}$inline$, то мы в качестве Q мы можем принять $inline$A^T+A$inline$.
Координаты векторов l и u задают границы изменения искомого вектора и лежат в диапазоне [-1,1]. Так как мы не предполагаем коротких продаж облигаций, то координаты векторов в нашем случае все не меньше 0. В приведенном ниже примере программы, для простоты, вектор l принят равным нулю, а коэффициенты вектора u все равны 0,3. Ничто, впрочем, не мешает усовершенствовать программу и сделать вектора ограничений более настраиваемыми.
Матрица С в нашем случае будет состоять из двух строк: 1) коэффициенты дисконтирования, которые при скалярном умножении на веса (то самое (w, k)) должны давать целевую ставку доходности портфеля; 2) строка, состоящая из единиц. Она нужна для задания ограничения $inline$\sum_{i}w_i=1$inline$.
Таким образом, выражение Cw*d для нашей задачи будет выглядеть так:
$$display$$\begin{equation} \left\{\begin{array}{ccc} ({\bf w, k}) = k_p \\ \sum_{i}w_i = 1 \\ \end{array} \right. ~~~~~~~~~~~~~(10) \end{equation}$$display$$
Перейдем теперь к программной реализации поиска оптимального портфеля. Основу квадратичного оптимизатора в ALGLIB составляет объект $inline$\tt \small minqpstate$inline$
alglib::minqpstate state;
Для инициализации оптимизатора этот объект передается функции minqpcreate вместе с параметром размерности задачи n
alglib::minqpcreate(n, state);
Следующим важнейшим моментом является выбор алгоритма оптимизации (солвера). Библиотека ALGLIB для квадратичной оптимизации предлагает три солвера:
- QP-BLEIC — наиболее универсальный алгоритм, предназначенный для решения задач с не очень большим (до 50 по рекомендациям документации) числом линейных ограничений (вида Cw*d). Может при этом быть эффективным на задачах большой размерности (как утверждает документация — до n=10000).
- QuickQP — очень эффективный алгоритм, особенно когда оптимизируется выпуклая функция. Однако, к сожалению, не может работать с линейными ограничениями — только с граничными условиями (вида l≤w≤u).
- Dense-AUL — оптимизирован для случая очень больших размерностей и большого количества ограничений. Но, по утверждению документации, задачи небольшой размерности и числа ограничений будут эффективней решаться с помощью других алгоритмов.
С учетом приведенных характеристик, очевидно, что для нашей задачи наиболее подходит солвер QP-BLEIC.
Для того, чтобы дать указание оптимизатору использовать данный алгоритм необходимо вызвать функцию $inline$\tt \small minqpsetalgobleic$inline$. Этой функции передаются сам объект и критерии остановки, на которых мы не будем подробнее останавливаться: в рассматриваемой здесь программе используются значения по-умолчанию. Вызов функции выглядит следующим образом:
alglib::minqpsetalgobleic(state, 0.0, 0.0, 0.0, 0);
Дальнейшая инициализация солвера включает:
- Передачу матрицы квадратичной части Q — $inline$\tt \small alglib: minqpsetquadraticterm (state, qpma);$inline$
- Передачу вектора линейной части (в нашем случае — нулевого вектора) — $inline$\tt \small alglib: minqpsetlinearterm (state, b);$inline$
- Передачу векторов граничных условий l и u — $inline$\tt \small alglib: minqpsetbc (state, bndl, bndu);$inline$
- Передачу линейных ограничений — $inline$\tt \small alglib: minqpsetlc (state, c, ct);$inline$
- Настройку масштаба координат векторного пространства $inline$\tt \small alglib: minqpsetscale (state, s);$inline$
Остановимся подробней на каждом пункте:
Для задания векторов и матриц в библиотеке ALGLIB применяются объекты специальных типов (целых и действительнозначных): $inline$\tt \small alglib: integer\_1d\_array$inline$, $inline$\tt \small alglib: real\_1d\_array$inline$, $inline$\tt \small alglib: integer\_2d\_array$inline$, $inline$ \tt \small alglib: real\_2d\_array$inline$. Для подготовки матрицы нам необходим тип $inline$\tt \small real\_2d\_array$inline$. В программе сначала создадим матрицу А ($inline$\tt \small alglib: real\_2d\_array~ qpma$inline$), а затем по формуле $inline$Q=A^T+A$inline$ из нее построим матрицу Q ($inline$\tt \small alglib: real\_2d\_array~ qpmq$inline$). Задание размерности матриц в ALGLIB производится отдельной функцией $inline$\tt \small setlength (n, m)$inline$.
Для построения матриц нам понадобятся вектора коэффициентов дисконтирования (ki) и отношения дюрации к этим коэффициентам ($inline$\frac{D_j}{k_j}$inline$):
std::vector disfactor;
std::vector durperytm;
Фрагмент кода, реализующий построение матриц приведен в следующем листинге:
size_t n = durations.size();
alglib::real_2d_array qpma; qpma.setlength(n,n); // matrix nxn
alglib::real_2d_array qpmq; qpmq.setlength(n,n); // matrix nxn
for(size_t j=0; j < n; j++)
{
for (size_t i = 0; i < n; i++) qpma(i,j) = durperytm[j]*disfactor[i]; //i,j элемент матрицы
}
for(size_t j=0; j < n; j++)
{
for (size_t i = 0; i < n; i++) qpmq(i,j) = qpma(i,j) + qpma(j,i);
}
Вектор линейной части, как уже было указано, в нашем случае нулевой, поэтому с ним всё просто:
alglib::real_1d_array b;
b.setlength(n);
for (size_t i = 0; i < n; i++) b[i] = 0;
Вектора граничных условий передаются одной функцией. Для решения рассматриваемой задачи применяются очень простые граничные условия: веса каждой бумаги не должны быть меньше нуля (мы не допускаем отрицательные позиции) и не должны превышать 30%. При желании ограничения можно усложнить. Эксперименты с программой показали, что даже простое изменение данного диапазона может сильно повлиять на результаты. Так, увеличение нижней границы и/или снижение верхней приводит к большей диверсификации итогового портфеля, ибо при оптимизации солвер может некоторые бумаги исключить из результирующего вектора (присвоить им вес 0%) как не подходящие. Если задать нижнюю границу весов, скажем, в 5%, то все бумаги гарантировано войдут в портфель. Однако расчетная дюрация при таких настройках будет, разумеется, больше, чем в случае, когда оптимизатор может исключать бумаги.
Итак, граничные условия задаются двумя векторами и передаются солверу:
alglib::real_1d_array bndl; bndl.setlength(n);
for (size_t i = 0; i < n; i++) bndl[i] = 0.0; // low boundary
alglib::real_1d_array bndu; bndu.setlength(n);
for (size_t i = 0; i < n; i++) bndu[i] = 0.3;// high boundary
alglib::minqpsetbc(state, bndl, bndu);
Далее оптимизатору необходимо передать линейные ограничения, задаваемые системой (10). В ALGLIB это делается с помощью функции $inline$\tt \small alglib: minqpsetlc (state, c, ct)$inline$, где с — это матрица, объединяющая левую и правую части системы (10), т.е. матрица вида $inline$(C ~~ d)$inline$, а ct — вектор отношений (т.е. соответствий вида ≥, = или ≤). В нашем случае ct = (0,0), что соответствует отношению '=' для обеих строк системы (10).
for (size_t i = 0; i < n; i++)
{
c(0,i) = disfactor[i]; //первая строка системы - коэффициенты дисконтирования облигаций
c(1,i) = 1; //вторая строка системы – единичная – для суммы весов
}
c(0,n) = target_rate; // первая строка (правая часть) – целевая доходность портфеля
c(1,n) = 1; // вторая строка (правая часть) – сумма весов, равная единице
alglib::integer_1d_array ct = "[0,0]"; // вектор отношений
alglib::minqpsetlc(state, c, ct);
Документация к библиотеке ALGLIB очень рекомендует задавать масштаб переменных перед запуском оптимизатора. Это особенно важно, если переменные измеряются в единицах, изменение которых отличается на порядки (например, при поиске решения, тонны могут изменяться в сотых или тысячных долях, а метры в единицах; задача при этом может решаться в пространстве «тонна-метр»), что влияет на критерии оставки. Есть, впрочем, оговорка, что при одинаковом шкалировании переменных, задание масштаба не обязательно. В рассматриваемой программе мы все же проводим задание масштаба ради большей строгости подхода, тем более, что сделать это очень просто.
alglib::real_1d_array s;
s.setlength(n);
for (size_t i = 0; i < n; i++) s[i] = 1; // масштаб всех переменных одинаков
alglib::minqpsetscale(state, s);
Далее зададим оптимизатору начальную точку. Вообще, этот шаг тоже не является обязательным, и программа благополучно справляется с поставленной задачей без заданной явно начальной точки. Аналогично, из соображений строгости начальную точку зададим. Мудрить не будем: начальной точкой будет являться точка с одинаковыми весами для всех облигаций.
alglib::real_1d_array x0;
x0.setlength(n);
double sp = 1/n;
for (size_t i = 0; i < n; i++) x0[i] = sp;
alglib::minqpsetstartingpoint(state, x0);
Остается определить переменную, в которую оптимизатор вернет найденное решение и переменную статуса. После чего можно запускать оптимизацию и обрабатывать результат
alglib::real_1d_array x; // результирующая точка
alglib::minqpreport rep; // статус
alglib::minqpoptimize(state); // запуск оптимизатора
alglib::minqpresults(state, x, rep); // получение статуса расчетов и результата
alglib::ae_int_t tt = rep.terminationtype;
if (tt>=0) // проверка на завершение оптимизации без ошибок
{
std::cout << "Веса облигаций в портфеле:" << '\n';
for(size_t i = 0; i < n; i++) // Выводим список облигаций с рассчитанными весами
{
std::cout << (i+1) << ".\t" << bonds[i].bondname << ":\t\t\t " << (x(i)*100) << "\%" << std::endl;
}
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
{
qpmq(i,j) /= 2;
}
}
}
Специально время работы программы в проводимых экспериментах не измерялось, но всё работает очень быстро. При этом, понятно, что частный инвестор вряд ли будет оптимизировать портфель более чем из 10–15 облигаций.
Важно еще заметить следующее. Оптимизатор возвращает именно вектор весов. Чтобы получить саму расчетную дюрацию необходимо непосредственно воспользоваться формулой (8). Программа умеет это делать. Для этого специально были добавлены две функции перемножения векторов и матриц. Здесь их приводить не будем. Желающие сами без труда найдут их в опубликованных исходных кодах.
На этом всё. Всем эффективных инвестиций в долговые инструменты.
P.S. Понимая, что ковыряния в чужом коде, занятие не самое привлекательное, а для многих людей, желающих заниматься инвестированием, и вовсе не профильное, постараюсь чуть позже переложить эту программу в форму простого веб-сервиса, которым смогут пользоваться все желающие независимо от знания математики и программирования.
