[Из песочницы] Оптимизация на примере. Имитационный отжиг против муравьиного алгоритма. Часть 1

Мне нравится сайт Хабр, особенно нравится как люди умеют грамотно излагать свои «технические» мысли на бумаге, чего не могу сказать о себе. Поэтому максимально постарался все описать в комментариях — мне так намного легче, да и Вам удобнее будет разобраться.
Код написан на MATLAB. При определенном написании синтаксис понять несложно. При написании алгоритмов старался сохранить баланс между «пониманием» кода и скоростью выполнения, исключив векторизацию, а где она есть — в комментариях написан альтернативный код. Если возникнут вопросы — постараюсь ответить в комментариях. Это первая часть серий «Оптимизация на примере», дальнейшие публикации будут выходить в зависимости от Ваших комментариев. То есть если нужно сравнение с другими эвристическими методами, либо если у Вас возникнет какое-то предложение (скажем изменить формулу температуры, либо начальное расположение муравьев), где можно доработать, а где изменить часть алгоритма — пишите. Будет интересно всем, да и мне тоже. Я же по возможности реализую и также опубликую.
Цель публикации, в первую очередь, показать на подробных комментариях в коде принцип работы двух алгоритмов, сравнение — второстепенная цель. В данной статье сравнить «чисто» не получится, так как в двух алгоритмах, особенно в муравьином, содержится приличное число начальных изменяемых параметров. Более того, возникли некоторые вопросы, но об этом чуть позже. В имитационном отжиге проще, однако, тоже есть свои нюансы. Для тех, кто только знакомится с данными алгоритмами рекомендую сначала ознакомиться с полезным материалом, расположенным в конце статьи.
Теория двух алгоритмов есть на Хабре да и на других сайтах, однако открытого кода муравьиного алгоритма с поясняющими комментариями толком не нашел, есть псевдокод, есть отдельные его части. Код же имитационного отжига на MATLAB был выложен ранее, однако, для сравнения с другими видами оптимизации у него небольшая скорость. Поэтому написал свой, увеличив скорость в разы. Оба алгоритма написал без встроенных собственных функций, потому что при небольшом коде, по-моему мнению, так воспринимать структуру алгоритма легче. В местах, где можно запутаться старался дать более развернутые комментарии. Исходя из этого, в теорию вдаваться не буду, приведу лишь следующее:
Имитационный отжиг
Метод имитации отжига отражает поведение материального тела при управляемом охлаждении. Как показали исследования, при отвердевании расплавленного материала его температура должна уменьшаться постепенно, вплоть до момента полной кристаллизации. Если процесс остывания протекает слишком быстро, образуются значительные нерегулярности структуры материала, которые вызывают внутренние напряжения. Быстрая фиксация энергетического состояния тела на уровне выше нормального аналогична сходимости оптимизационного алгоритма к точке локального минимума. Энергия состояния тела соответствует целевой функции, а абсолютный минимум этой энергии — глобальному минимуму [1].
Муравьиный алгоритм
Один из эффективных полиномиальных алгоритмов для нахождения приближённых решений задачи коммивояжёра, а также решения аналогичных задач поиска маршрутов на графах. Суть подхода заключается в анализе и использовании модели поведения муравьёв, ищущих пути от колонии к источнику питания и представляет собой метаэвристическую оптимизацию [2].
Есть множество модификаций муравьиных алгоритмов. Где-то разное обновление феромонов, где-то имеются «элитные» муравьи, а где-то различные расположения муравьев при старте. В коде просто что-то закомментируйте, что-то раскомментируйте.
% метод отжига ( на примере задачи коммивояжера )
%--------------------------------------------------------------------------
tic
% clearvars -except cities
clearvars
% -----------------------------ИТЕРАЦИИ------------------------------------
% кол-во итераций
m = 100000;
% -----------------------------ПАРАМЕТРЫ-----------------------------------
% начальная температура
Tstart = 10000;
% конечная температура
Tend = 0.1;
% начальная температура для вычислений
T = Tstart;
% расстояние
S = inf;
% количество городов
n = 100;
% --------------------------------ПАМЯТЬ-----------------------------------
% матрица расстояний
dist = zeros(n,n);
% -------------------------------------------------------------------------
% генерация городов (x,y)
cities = rand(n,2)*100;
% задаем случайный маршрут
ROUTE = randperm(n);
% создаем матрицу расстояний
for i = 1:n
for j = 1:n
% dist ( расстояния )
dist(i,j) = sqrt((cities(i,1) - cities(j,1))^2 + ...
(cities(i,2) - cities(j,2))^2);
end
end
% поехали оптимизировать, время от кол-ва итераций
for k = 1:m
% сбрасываем потенциальное расстояние
Sp = 0;
% здесь условие создания потенциальных маршрутов, ROUTEp -
% потенциальный маршрут
% потенциальный маршрут
ROUTEp = ROUTE;
% два случайных города
transp = randperm(n,2);
% переворот вектора, взяли два сгенерированных числа transp и
% перевернули маршрут между ними
if transp(1) < transp(2)
ROUTEp(transp(1):transp(2)) = fliplr(ROUTEp(transp(1):transp(2)));
else
ROUTEp(transp(2):transp(1)) = fliplr(ROUTEp(transp(2):transp(1)));
end
% вычисляем энергию (расстояние) потенциального маршрута
for i = 1:n-1
Sp = Sp + dist(ROUTEp(i),ROUTEp(i+1));
end
Sp = Sp + dist(ROUTEp(1),ROUTEp(end));
% если он меньше то, потенциальный маршрут становится основным ...
% если нет, смотрим, осуществляется ли переход
if Sp < S
S = Sp;
ROUTE = ROUTEp;
else
% случайно выбранное число от 0 до 1
RANDONE = rand(1);
% вычисляем вероятность перехода
P = exp((-(Sp - S)) / T);
if RANDONE <= P
S = Sp;
ROUTE = ROUTEp;
end
end
% уменьшаем температуру
T = Tstart / k;
% проверяем условие выхода
if T < Tend
break;
end;
end
% рисуем графику
citiesOP(:,[1,2]) = cities(ROUTE(:),[1,2]);
plot([citiesOP(:,1);citiesOP(1,1)],[citiesOP(:,2);citiesOP(1,2)],'-r.')
% очищаем переменые
clearvars -except cities ROUTE S
% смотрим время
toc
% муравьиный алгоритм ( на примере задачи коммивояжера )
% -------------------------------------------------------------------------
tic
% clearvars -except cities
clearvars
% ------------------------------ИТЕРАЦИИ-----------------------------------
% кол-во итераций ( поколений )
age = 50;
% кол-во муравьев в поколении
countage = 30;
% кол-во городов
n = 30;
% ------------------------------ПАРМЕТРЫ-----------------------------------
% альфа - коэффициент запаха, при 0 будем ориентироваться только на
% кратчайший путь
a = 1;
% бета - коэффициент расстояния, при 0 будем
% ориентироваться только на оставляемый запах
b = 2.5;
% коэффициент испарения ( память поколений )
e = 0.5;
% количество выпускаемых феромонов
Q = 1;
% кол-во элитных муравьев ( увеличение лучшей дистанции в elite раз )
elite = 1;
% начальный феромон
ph = 0.01;
% -------------------------------ПАМЯТЬ------------------------------------
% матрица расстояний
dist = zeros(n,n);
% матрица обратных расстояний
returndist = zeros(n,n);
% матрица маршрута муравьев в одном поколении
ROUTEant = zeros(countage,n);
% вектор расстояний муравьев в одном поколении
DISTant = zeros(countage,1);
% вектор лучших дистанций на каждой итерации
bestDistVec = zeros(age,1);
% лучший начальный маршрут
bestDIST = inf;
% оптимальные маршруты
ROUTE = zeros(1,n+1);
% перестановка городов без повторений ( для выхода муравьев )
RANDperm = randperm(n);
% матрица вероятностей
P = zeros(1,n);
% -------------------------------------------------------------------------
% генерация городов (x,y)
cities = rand(n,2)*100;
% матрица начальных феромонов
tao = ph*(ones(n,n));
% создаем матрицу расстояний и матрицу обратных расстояний
for i = 1:n
for j = 1:n
% dist ( расстояния )
dist(i,j) = sqrt((cities(i,1) - cities(j,1))^2 + ...
(cities(i,2) - cities(j,2))^2);
% nn ( обратные расстояния )
if i ~= j
returndist(i,j) = 1/sqrt((cities(i,1) - cities(j,1))^2 + ...
(cities(i,2) - cities(j,2))^2);
end
end
end
% итерации
for iterration = 1:age
% муравьи ( одно поколение)
for k = 1:countage
% ****************** НАЧАЛЬНОЕ РАСПОЛОЖЕНИЕ МУРАВЬЕВ ******************
% выбирайте какой нужно
% каждый муравей располагается случайно
% ROUTEant(k,1) = randi([1 n]);
% с каждого города выходит один муравей ( без совпадений ), кол-во
% городов и кол-во муравьев в поколении должны быть равны
ROUTEant(k,1) = RANDperm(k);
% с конкретного города выходят все муравьи в данном случа с 1-ого
% ROUTEant(k,1) = 1;
% тут маршрут первому поколению задаем либо произвольный, либо с каждого
% города разный, либо с одного города все, а следующее поколение выходит по
% концам первых
% if iterration == 1
% ROUTEant(k,1) = randi([1 n]);
% % ROUTEant(k,1) = RANDperm(k);
% % ROUTEant(k,1) = 1;
% else
% ROUTEant(k,1) = lastROUTEant(k);
% end
% *********************************************************************
% путь каждого муравья, начиная со второго, так как первый выбран
for s = 2:n
% полуаем индекс выбранного города
ir = ROUTEant(k,s-1);
% вероятность посещения городов ( числитель ) , в числителе у нас
% следующее: tao^a*(1/S)^b
% 1/S -это returndist.
% поскольку данное значение будет повторяться (кол-во муравьев * на
% колонию * кол-во городов) раз, то еще один цикл писать не выгодно,
% скорость работы при таких вычислениях падает. Поэтому написал в
% этом моменте векторно. На обычном языке будет так:
% for c = 1:n
% P(1,c) = tao(ir,c).^a * returndist(ir,c).^b;
% end
P = tao(ir,:).^a .* returndist(ir,:).^b;
% получили числители (в формуле вероятности перехода к k-ому городу)
% для n городов, однако в некоторых мы уже побывали, нужно исключить
% их
% проставляем нули в числитель туда, где уже были, чтобы
% вероятность перехода была 0, следовательно в сумме знаменателя
% формулы данный город учитываться не будет
P(ROUTEant(k,1:s-1)) = 0;
% получаем вероятности перехода ( сумма строк должна быть = 1 )
P = P ./ sum(P);
% смотрим в какой город осуществляется переход
RANDONE = rand;
getcity = find(cumsum(P) >= RANDONE, 1, 'first');
% если с вероятностями что-то не так, выдача ошибки
if isempty(getcity) == 1
disp 'Ошибка в вероятностях!'
end
% присваем s-ый город в путь k-ому муравью
ROUTEant(k,s) = getcity;
end
% получаем маршрут k-ого муравья
ROUTE = [ROUTEant(k,1:end),ROUTEant(k,1)];
% сброс длины
S = 0;
% вычисляем маршрут k-ого муравья
for i = 1:n
S = S + dist(ROUTE(i),ROUTE(i+1));
end
% путь k-ого муравья, массив дистанций k-ых муравьев
DISTant(k) = S;
% присваевыем лучший маршрут и S
if DISTant(k) < bestDIST
bestDIST = DISTant(k);
bestROUTE = ROUTEant(k,1:end);
end
% вектор "последних" городов k-ых муравьев ( выбирается для старта
% муравьев нового поколения с тех городов, где закончили путь
% предыдущее поколение)
% lastROUTEant = ROUTEant(1:end,end);
end
% -----------------------ИЗМЕНЯЕМ КОЛИЧЕСТВО ФЕРОМОНОВ---------------------
% Испаряем феромоны "старого" пути е - коэффициент испарения
tao = (1-e)*tao;
for u = 1:countage
% получаем маршрут u-ого муравья
ROUTE = [ROUTEant(u,1:end), ROUTEant(u,1)];
% для каждого города
for t = 1:n
x = ROUTE(t);
y = ROUTE(t+1);
% считаем новый феромон
if DISTant(u) ~= max(DISTant)
% тут по формуле добавки феромона в зависимости от
% дистанции
tao(x,y) = tao(x,y) + Q / DISTant(u);
else
% усиливаем ребера лучшего пути
tao(x,y) = tao(x,y) + (elite*Q) / DISTant(u);
end
end
end
end
% строим графику
citiesOP(:,[1,2]) = cities(bestROUTE(:),[1,2]);
plot([citiesOP(:,1);citiesOP(1,1)],[citiesOP(:,2);citiesOP(1,2)],'.r-')
clearvars -except cities ROUTE bestDIST bestROUTE ROUTEant
toc
Итак, давайте сравним, сгенерируем для начала 30 городов.
Имитационный отжиг:
Параметры:
- Количество городов — 30
- Начальная температура — 10 000
- Конечная температура — 0,01
- Формула температуры — начальную температуру / k-ую итерацию
- Число итераций — 100 000
- Функция вероятности принятия — exp (-ΔE/T)
- Определение потенциального маршрута (порождающего семейства) — разворот части вектора (текущего маршрута) от двух случайно выбранных чисел равномерным распределением
Теперь посмотрим на работу муравьиного алгоритма на тех же координатах.
Муравьиный алгоритм:
Параметры:
- Количество итераций (поколений) — 60
- Количество муравьев в поколении — 30
- Количество городов — 30
- альфа (коэф. ориентации на феромоны) — 0,85
- бета (коэф. ориентации на длину пути) — 3,8
- е (коэф. испарение феромонов) — 0,5
- elite (количество элитных муравьев) — нет
- расположение муравьев в первых городах — разные, без повторений. Кол-во городов = числу муравьев в поколении
- обновление феромонов — глобальное (феромоны обновляются после прохода 1-ого поколения)
- вероятность перехода из одной вершины в другую —
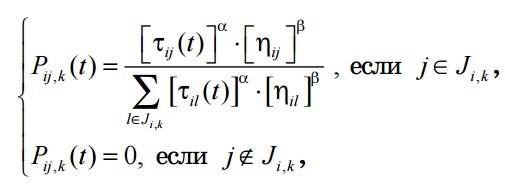
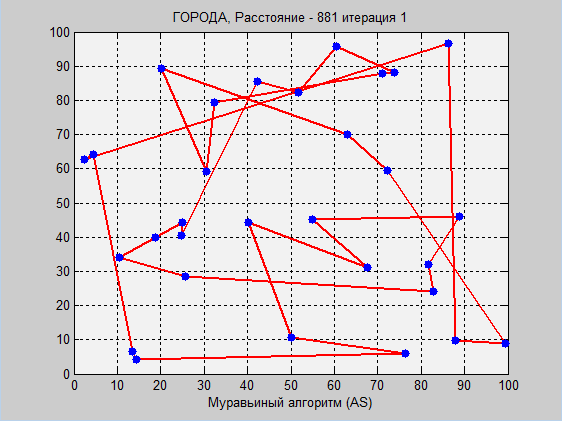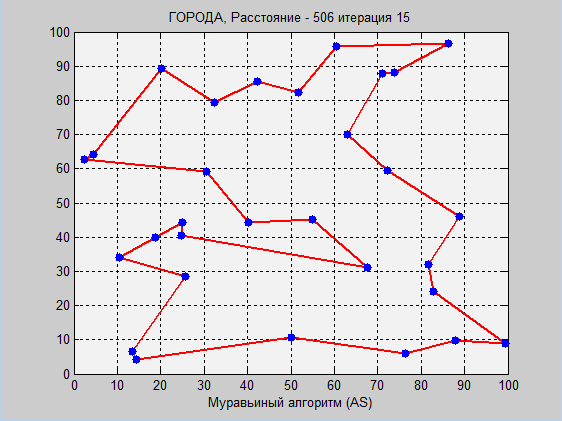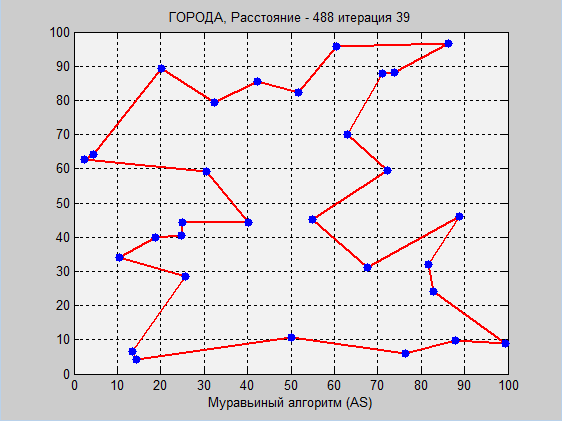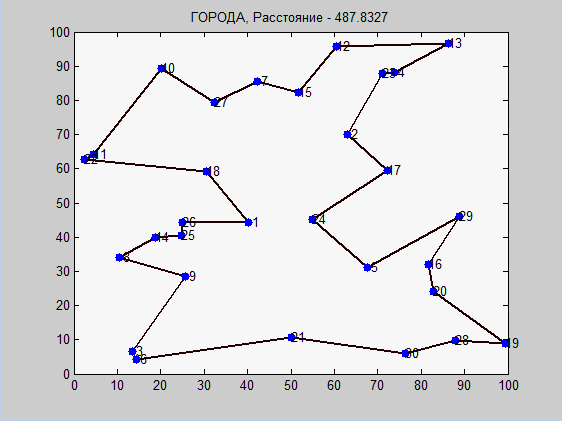
Перед Вами наглядная работа двух алгоритмов. Еще раз отмечу, что подробное объяснение (особенно муравьиного алгоритма) в комментариях кода.
Обратите внимание, что в имитационном отжиге оптимум нашелся уже на 20000 итерации, дальше, когда температура стала достаточно низкой, вероятность перехода на новые маршруты значительно снизилась, поэтому алгоритм «встал». Тут можно ввести критерии остановки. Чем выше начальная температура, тем больше вероятность попасть на оптимальный маршрут, и тем больше итераций будет совершено, однако, далеко не факт, что мы найдем глобальный оптимум.
В муравьином алгоритме же все иначе. Главный плюс муравьиного алгоритма заключается в том, что он никогда не остановится, он всегда будет искать лучшие пути. При бесконечном числе итераций (поколений) вероятность найти глобальный оптимум будет стремиться к 1. Однако, уже в самом начале встал вопрос: какие начальные параметры выбрать? Ответ: методом подбора. Снова оптимизируем. Данные параметры муравьиной оптимизации оптимизировал с помощью генетического алгоритма не на данных координатах. Там были другие координаты и количество городов было 50. Толком не получив хорошей сходимости, получил некоторые параметры, которые примерно соответствуют на данном примере.
На одном тесте далеко не уехать, поэтому привожу таблицу из серий тестов.

Видно стабильность двух алгоритмов, однако разброс от среднего значения у муравьиного алгоритма меньше.
Теперь посмотрим работу двух алгоритмов на 100 сгенерированных городов.
Имитационный отжиг:
Параметры:
- Количество городов — 100
- Начальная температура — 42 000
- Конечная температура — 0,01
- Формула температуры — начальную температуру / k-ую итерацию
- Число итераций — 420 000
- Функция вероятности принятия — exp (-ΔE/T)
- Определение потенциального маршрута (порождающего семейства) — разворот части вектора (текущего маршрута) от двух случайно выбранных чисел равномерным распределением
Теперь посмотрим на работу муравьиного алгоритма на тех же координатах.
Муравьиный алгоритм:
Параметры:
- Количество итераций (поколений) — 50
- Количество муравьев в поколении — 100
- Количество городов — 100
- альфа (коэф. ориентации на феромоны) — 1
- бета (коэф. ориентации на длину пути) — 3
- е (коэф. испарение феромонов) — 0,5
- elite (количество элитных муравьев) — нет
- расположение муравьев в первых городах — разные, без повторений. Кол-во городов = числу муравьев в поколении
- обновление феромонов — глобальное (феромоны обновляются после прохода 1-ого поколения)
Здесь параметры взял «на глаз».
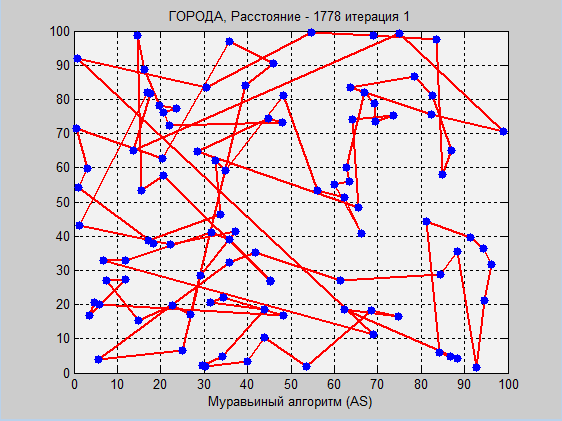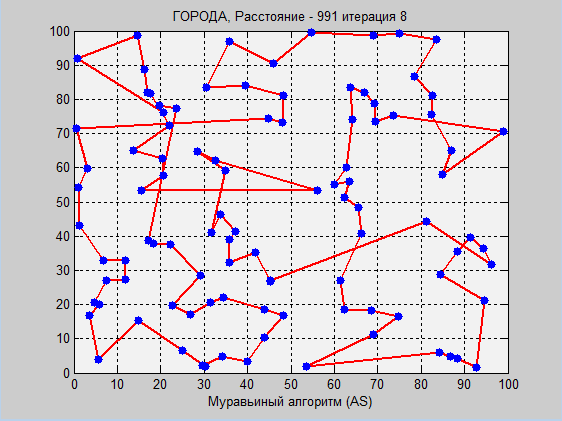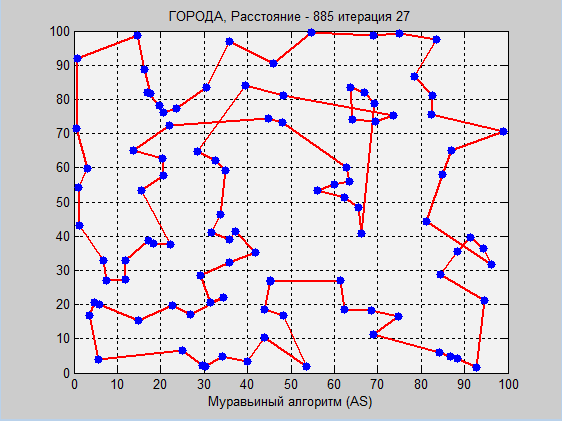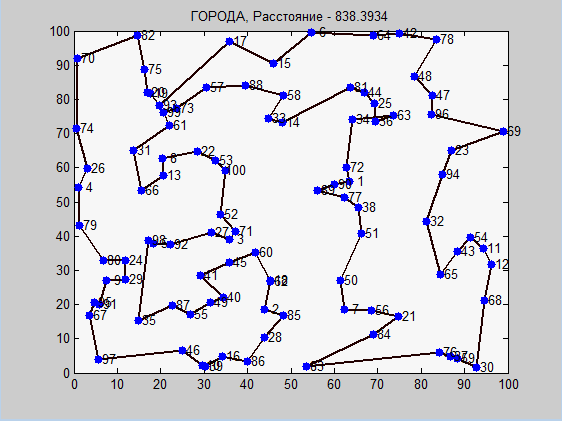
Снова муравьиный алгоритм показал результат получше, однако, давайте снова посмотрим на таблицу из серий тестов:
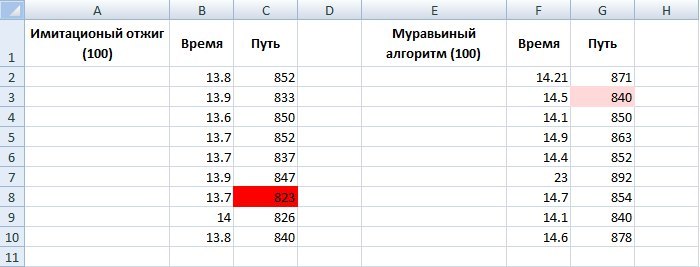
Здесь далеко ушел вперед имитационный отжиг. Вообще, до того как я прочитал статью, к имитационному отжигу относился скептически. В разработке торговых систем (в чем я замешан) и их оптимизации метод отжига не подходит, так как нам важен не сам локальный оптимум, а «разброс» вокруг него. На условном примере: есть скользящая средняя в 15 дней на какой-то бумаге, за год доходность показала 10000, а при 14 днях (-1000). Здесь нам важно, чтобы около параметра оптимального равномерно убывала прибыль. Поэтому в разных ситуациях — разная оптимизация.
Что касается задачи коммивояжера, то я, пусть даже и не в «чистом» соревновании (потому как правильно подобрать параметры для муравьиного алгоритма не вышло), отдаю победу имитационному отжигу. При добавлении критерия остановки, тех же расстояний без особого изменения стандартного отклонения можно добиться за 2,5 секунды, чего не скажешь о муравьином алгоритме. По серии тестов, значительная часть которых не попала сюда, муравьиный алгоритм блестяще работает до 50 городов, дальше начинает «моросить», время оптимизации сильно замедляется, что в принципе и логично. Однако он уверено идет к глобальному оптимуму, пусть даже и медленно.
Где-то в глубине души все равно хочется, чтобы муравьиный алгоритм проявил себя лучше. Может быть поэтому не покидает чувство, что допустил где-то ошибку, и не одну. Поэтому те, кого заинтересовал, и те, кто только начинает путь в этом направлении — присоединяйтесь. Пишите комментарии с предложениями, как по поводу алгоритмов, так и по поводу того, как лучше подавать материал.
А пока посмотрим на сегодняшнего победителя. 500 городов, 86 секунд оптимизации (и это далеко не предел).
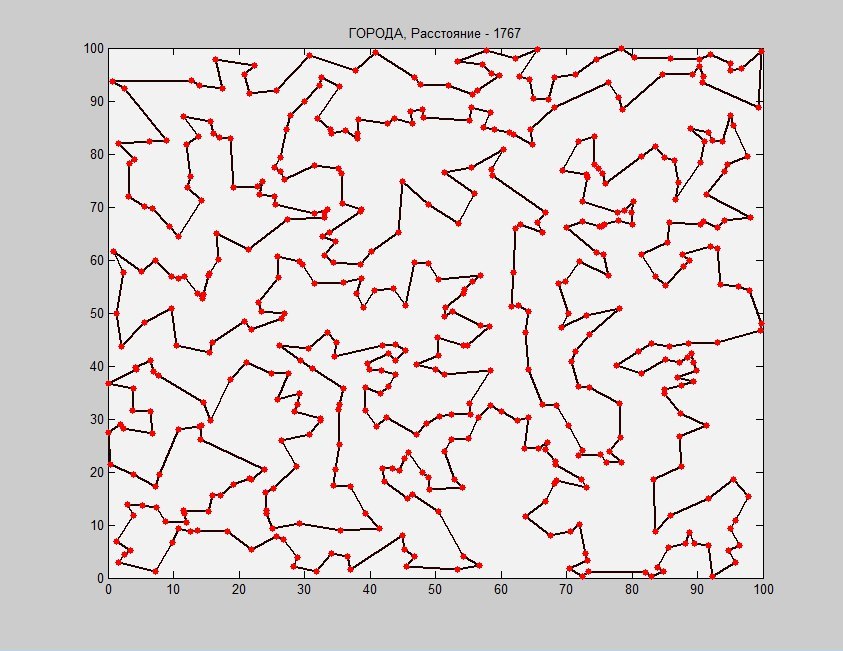
Очень круто!
Догонит или нет муравьиный алгоритм? Обгонит ли его генетический? Кто будет эффективнее? Об этом и другом в следующих публикациях.
Полезный материал:
» Видео про муравьиный алгоритм (на русском)
» Видео про имитационный отжиг (на русском)
» Статья про муравьиный алгоритм (на русском)
» Статья про имитационный отжиг (на русском)
