[Из песочницы] О разрешимости beltway проблемы в полиномиальное время
С beltway проблемой студенты знакомятся, проходя курсы биоинформатики, в частности, один из наиболее качественных и наиболее близкий по духу для программистов — курс Bioinformatics (Павла Певзнера) на coursera от University of California San Diego. Проблема привлекает внимание простотой постановки, практической важностью, ну и тем, что она до сих пор считается нерешенной при кажущейся возможностью решить ее простым кодированием. Проблема ставится таким образом. Возможно ли в полиномиальное время восстановить координаты множества точек $inline$X$inline$, если известно множество всех парных расстояний между ними $inline$\Delta X$inline$?
Эта с виду простая задача до сих пор находится в списке нерешенных проблем вычислительной геометрии. Причем ситуация даже не касается точек в многомерных пространствах, тем более искривленных, проблемой является уже самый простой вариант — когда все точки имеют целочисленные координаты и локализованы на одной линии.
За прошедшие почти полвека с тех пор, как эта задача была осознана математиками как вызов (Shamos, 1975), были получены некоторые результаты. Рассмотрим два случая возможных для одномерной задачи:
- точки расположены на прямой (turnpike проблема)
- точки расположены на окружности (beltway проблема)
Эти два случая получили разные названия не просто так — требуются различные усилия, чтобы их решить. И действительно, первая задача была решена достаточно быстро (за 15 лет) и построен backtracking алгоритм, восстанавливающий решение в среднем за квадратичное время $inline$O (n^2 \log n)$inline$, где $inline$n$inline$ — число точек (Skiena, 1990); для второй задачи этого сделать не удалось до сих пор, и лучший предложенный алгоритм имеет экспоненциальную вычислительную сложность $inline$O (n^n \log n)$inline$ (Lemke, 2003). На картинке ниже приведена оценка того, как долго будет работать ваш компьютер, чтобы получить решение для множества с разным числом точек.

То есть, за психологически приемлемое время (~10 сек) можно восстановить множество $inline$X$inline$ объемом до 10 тысяч точек в turnpike случае и только ~10 точек для beltway случая, что совершенно никуда не годится для практических приложений.
Небольшое уточнение. Считается, что turnpike проблема решена с точки зрения использования в практике, то есть для подавляющего большинства встречаемых данных. При этом игнорируются возражения чистых математиков на то, что существуют специальные наборы данных для которых время получения решения экспоненциально $inline$O (2^n \log n) $inline$ (Zhang, 1982). В противоположность turnpike, beltway проблема с ее экспоненциальным алгоритмом никак не может считаться решенной практически.
Важность решение beltway проблемы с точки зрения биоинформатики
В конце 20 века был обнаружен новый путь синтеза биомолекул, названный нерибосомальным путем синтеза. Главное его отличие от классического пути синтеза в том, что конечный результат синтеза вообще не закодирован в ДНК. Вместо этого, в ДНК записан только код «инструментов» (множества различных синтетаз), которые могут собирать эти объекты. Таким образом, биомашинная инженерия существенно обогащается, и клетке вместо одного типа сборщика (рибосомы), выполняющего работы только с 20 стандартными деталями (стандартные аминокислоты, также называемые протеиногенными) появляются множество других типов сборщиков, которые могут работать с более чем 500 стандартными и нестандартными деталями (непротеиногенные аминокислоты и различные их модификации). И эти сборщики могут не просто соединять детали в цепочки, но и получать весьма замысловатые конструкции — циклические, ветвящиеся, а также конструкции со многими циклами и ветвлением. Все это существенно повышает арсенал клетки на разные случаи ее жизни. Биологическая активность таких конструкций высока, специфичность (избирательность действия) тоже, разнообразие свойств — не ограничено. Класс этих продуктов клетки в англоязычной литературе имеет название NRPs (non-ribosomal products, или non-ribosomal peptides). Биологи надеются, что именно среди таких продуктов метаболизма клетки можно найти новые фармакологические препараты, обладающие высокой эффективностью и за счет специфичности не имеющие побочных эффектов.
Вопрос состоит только в том, а как и где искать NRPs? Они весьма эффективны, следовательно клетке совершенно незачем продуцировать их в большом количестве, и концентрации их ничтожны. Значит химические методы извлечения с их низкой точностью ~1% и огромными затратами по реактивам и времени бесполезны. Далее. Они не кодированы в ДНК, значит все базы данных, что накоплены при расшифровке генома, и все методы биоинформатики и геномики также бесполезны. Единственным способом что-то найти остаются физические методы, а, именно, масс-спектроскопия. Тем более, что уровень обнаружения вещества у современных спектрометров настолько высок, что позволяет найти ничтожные количества, всего >~ 800 молекул (атто-молярный диапазон, или концентрации $inline$10^{-18}$inline$).
 »
»
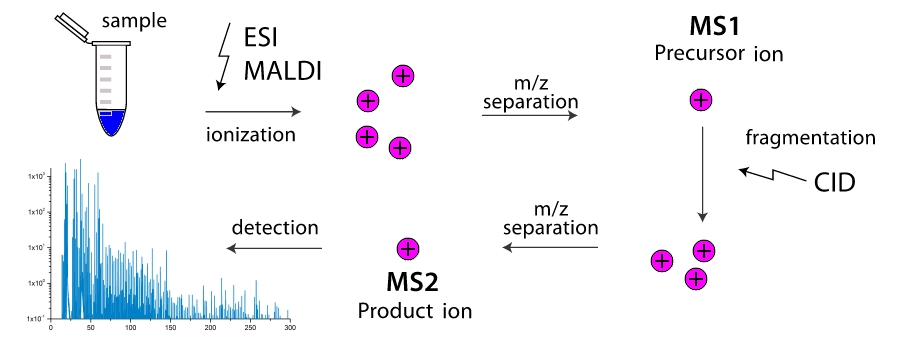
А как работает масс-спектрометр? В рабочей камере прибора происходит разрушение молекул на фрагменты (чаще путем их столкновений друг с другом, реже за счет внешнего воздействия). Эти фрагменты ионизуются, а затем разгоняются и разделяются во внешнем электромагнитном поле. Разделение происходит либо по времени достижения детектора, либо по углу разворота в магнитном поле, ведь больше масса фрагмента и ниже его заряд, тем более неповоротливым он является. Таким образом, масс-спектрометр как бы «взвешивает» массы фрагментов. Причем, «взвешивание» можно сделать многоэтапным, многократно отфильтровывая фрагменты с одной массой (точнее с одним значением $inline$m/z$inline$) и прогоняя их через фрагментацию с дальнейшим разделением. Двухэтапные масс-спектрометры широко распространены и называются тандемными, многоэтапные — крайне редки, и просто обозначаются как $inline$МС^n$inline$, где $inline$n$inline$ — число этапов. А вот тут то и появляется задача, как зная только массы всевозможных фрагментов какой либо молекулы узнать ее структуру? Вот мы и пришли к turnpike и beltway проблемам, для линейных и циклических пептидов, соответственно.
Поясню более детально, как задача восстановления структуры биомолекулы сводится к указанным проблемам на примере циклического пептида.
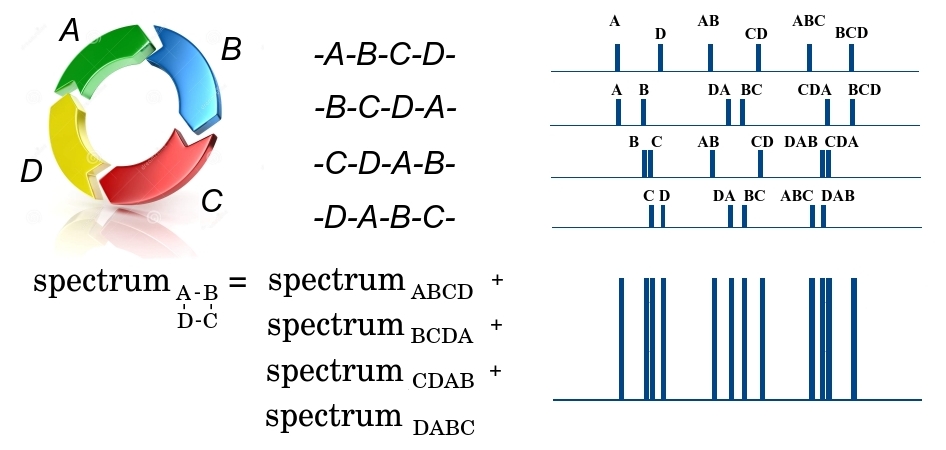
Циклический пептид ABCD на первом этапе фрагментации может быть разорван в 4-х местах, либо по связи D-A, либо по A-B, B-C или C-D, образуя 4 возможных линейных пептида — либо ABCD, BCDA, CDAB или DABC. Поскольку через спектрометр проходит огромное число одинаковых пептидов, то на выходе будем иметь фрагменты всех 4-х типов. Причем заметим, что все фрагменты имеют одинаковую массу, и не могут быть разделены на первом этапе. На втором этапе, линейный фрагмент ABCD может быть разорван в трех местах, образуя более мелкие фрагменты с разной массой A и BCD, AB и CD, ABC и D, и формируя соответствующий масс-спектр. В этом спектре по оси x откладывается масса фрагмента, а по оси y — число мелких фрагментов с данной массой. Аналогично формируются спектры для остальных трех линейных фрагментов BCDA, CDAB и DABC. Так как все 4 крупных фрагмента прошли на второй этап, то все их спектры складываются. Итого, на выходе получается некоторое множество масс $inline$\{m_1^{n_1}, m_2^{n_2}, …, m_q^{n_q}\}$inline$, где $inline$m_i$inline$ — некоторая масса, а $inline$n_i$inline$ — кратность ее повторения. При этом мы не знаем, к какому фрагменту относится эта масса и уникален ли этот фрагмент, поскольку различные фрагменты могут иметь одну массу. Чем далее связи в пептиде находятся друг от друга, тем большая масса фрагмента пептида находится между ними. То есть, задача восстановления порядка элементов в циклическом пептиде сводится к beltway проблеме, в которой элементами множества $inline$X$inline$ являются связи в пептиде, а элементами множества $inline$\Delta X$inline$ — массы фрагментов между связями.
Предчувствие возможности существования алгоритма с полиномиальным временем решения beltway проблемы
Из своего опыта и из общения с людьми, кто пытался или реально что-то сделал для решения этой проблемы, я заметил, что подавляющее большинство людей пытаются решить ее либо в общем случае, либо для целочисленных данных в узком диапазоне, вроде такого (1, 50). Оба варианта обречены на неудачу. Для общего случая было доказано, что полное число решений для beltway проблемы в одномерном случае $inline$ S_1(n) $inline$ ограничено значениями (Lemke, 2003)
$$display$$e^{2^{\frac{\ln n}{\ln \ln n} + o (1)}} \leq S_1(n) \leq \frac{1}{2} n^{n-2}$$display$$
что означает наличие экспоненциального числа решений в асимптотике $inline$n \rightarrow \infty$inline$. Очевидно, что если число решений растет по экспоненте, то и время их получения медленней расти не может. То есть для общего случая получить полиномиальное время решение невозможно. Что же касается целочисленных данных в узком диапазоне, то здесь все можно проверить экспериментально, поскольку не слишком сложно написать код, который ищет решение методом полного перебора. Для небольших $inline$n$inline$ такой код будет считать не очень долго. Результаты испытания такого кода покажут, что при таких условиях на данные полное число различных решений для любого множества $inline$\Delta X$inline$ уже при малых $inline$n$inline$ также растет крайне резко.
Узнав о этих фактах можно смириться и махнуть рукой на эту задачу. Допускаю, что это является одной из причин по которой beltway проблема до сих пор считается нерешенной. Однако лазейки все же существуют. Вспомним, что экспоненциальная функция $inline$e^{\alpha x}$inline$ ведет себя очень интересно. Сначала она растет страшно медленно, поднимаясь от 0 до 1 за бесконечно большой промежуток от $inline$\infty$inline$ до 0, затем ее рост все более и более ускоряется. Однако, чем меньше значение $inline$\alpha$inline$, тем больше должно быть значение $inline$x$inline$, чтобы результат функции перешагнул некоторое заданное значение $inline$y = \xi $inline$. В качестве такого значения удобно выбрать число $inline$\xi = 2$inline$, до него решение единственное, после него решений много. Вопрос. А проверял ли кто-нибудь зависимость числа решений от того, какие данные попадают на вход? Да, проверял. Есть замечательная phD диссертация хорватской женщины математика Тамары Дакис (Dakic, 2000), в которой она определила каким условиям должны удовлетворять входные данные, чтобы проблема решалась в полиномиальное время. Наиболее важные из них — единственность решения и отсутствие дублирования во множестве входных данных $inline$\Delta X$inline$. Уровень ее phD диссертации очень высок. Очень жаль, что эта студентка ограничилась только turnpike проблемой, убежден, что обрати она свой интерес к beltway проблеме та давно была бы решена.
Получение алгоритма с полиномиальным временем решения beltway проблемы
Обнаружить данные для которых возможно построить нужный алгоритм удалось случайно. Потребовались дополнительные идеи. Основная идея возникла из наблюдения (см. выше), что спектр циклического пептида является суммой спектров всех линейных пептидов, которые образуются при однократных разрывах кольца. Поскольку последовательность аминокислот в пептиде может быть восстановлена из любого такого линейного пептида, то полное число линий в спектре существенно (в $inline$n$inline$ раз, где $inline$n$inline$ — число аминокислот в пептиде) избыточно. Вопрос заключается только в том, какие линии нужно исключить из спектра, чтобы не потерять возможность восстановления последовательности. Поскольку математически обе задачи (восстановления последовательности циклического пептида из масс-спектра и beltway проблема) изоморфны, то так же можно прореживать множество $inline$\Delta X$inline$.
Операции прореживания $inline$\Delta X$inline$ были построены с использованием локальных симметрий множества $inline$\Delta X$inline$ (Fomin, 2016a).
- Симметризация. Первая операция заключается в том, чтобы выбрать произвольный элемент множества $inline$ x_{\mu} \in \Delta X$inline$ и удалить из $inline$\Delta X$inline$ все элементы, кроме тех, которые имеют симметричные пары относительно точек $inline$ x_{\mu}/2$inline$ и $inline$ (L + x_{\mu})/2 $inline$, где $inline$L$inline$ — длина окружности (напомню, что в beltway случае все точки расположены на окружности).
- Конволюция по частичному решению. Вторая операция использует наличие догадки о решении, то есть знание отдельных точек, которые принадлежат решению, так называемое частичное решение. Здесь из множества $inline$\Delta X$inline$ также удаляются все элементы, кроме тех, которые удовлетворяют условию — если мы измерим расстояния от проверяемой точки до всех точек частичного решения, то все полученные значения имеются в $inline$\Delta X$inline$. Уточню, что если хотя бы одно из полученных расстояний отсутствует в $inline$\Delta X$inline$, то точка игнорируется.
Были доказаны теоремы, что обе операции прореживают множество $inline$\Delta X$inline$, но в нем все равно останется достаточно элементов для восстановления решения $inline$X$inline$. С использованием этих операция был построен и реализован на c++ алгоритм для решения beltway проблемы (Fomin, 2016b). Алгоритм мало отличается от классического backtracking алгоритма (то есть пытаемся строить решение путем перебора возможных вариантов и делаем возвраты, если при построении получили ошибку). Отличие заключается только в том, что для счет сужения множества $inline$\Delta X$inline$ опробовать нам становится существенно меньше вариантов.
Вот пример, как резко сужается множество $inline$\Delta X$inline$ при прореживании.

Вычислительные эксперименты выполнялись для случайно генерированных циклических пептидов длиной $inline$n$inline$ от 10 до 1000 аминокислот (ось ординат в логарифмическом масштабе). По оси абсцисс также в логарифмическом масштабе отложено число элементов в прореженных разными операциям множествах $inline$\Delta X$inline$ в единицах $inline$n$inline$. Такое представление абсолютно непривычно, потому расшифрую, как это читается на примере. Смотрим левую диаграмму. Пусть пептид имеет длину $inline$n=100$inline$. Для него число элементов во множестве $inline$\Delta X$inline$ равно $inline$n^2 = 10000$inline$ (это точка на верхней пунктирной прямой $inline$y=n^2$inline$). После удаления из множества $inline$\Delta X$inline$ повторяющихся элементов, число элементов в $inline$\Delta X$inline$ уменьшается до $inline$n_D \approx n^{1.9} \approx 6300$inline$ (кружки с крестиками). После симметризации число элементов падает до $inline$n_S \approx n^{1.75} \approx 3100$inline$ (черные кружки), а после конволюции по частичному решению до $inline$n_C \approx n^{1.35} \approx 500$inline$ (крестики). Итого, общий объем множества $inline$\Delta X$inline$ сокращается всего в 20 раз. Для пептида такой же длины, но на правой диаграмме, сокращение происходит от $inline$n^2 = 10000$inline$ до $inline$N_C \approx n \approx 100$inline$, то есть в 100 раз.
Заметим, что генерация тестовых примеров для левой диаграммы выполняется таким образом, чтобы уровень дублирования $inline$k_{dup}$inline$ в $inline$\Delta X$inline$ был в диапазоне от 0.1 до 0.3, а для правой — менее 0.1. Уровень дублирования определяется как $inline$k_{dup} = 2-\log {N_u}/ \log{n}$inline$, где $inline$N_u$inline$ — число уникальных элементов во множестве $inline$\Delta X$inline$. Такое определение дает естественный результат: при отсутствии дубликатов во множестве $inline$\Delta X$inline$ его мощность равна $inline$N_u = n^2$inline$ и $inline$k_{dup} = 0$inline$, при максимально возможном дублировании $inline$N_u = n$inline$ и $inline$k_{dup} = 1$inline$. Как сделать обеспечить разный уровень дублирования, скажу чуть позже. По диаграммам видно, что чем меньше уровень дублирования, тем сильнее прореживается $inline$\Delta X$inline$, при $inline$k_{dup} < 0.1$inline$ число элементов в прореженном $inline$\Delta X$inline$ вообще достигает своего предела $inline$O(n^2) \rightarrow O(n)$inline$, поскольку в прореженном множестве меньше чем $inline$O(n)$inline$ элементов получить невозможно (операции сохраняют достаточно элементов, чтобы получить решение, в котором $inline$n$inline$ элементов). Факт сужения мощности множества $inline$\Delta X$inline$ до нижнего предела очень важен, именно он приводит к кардинальным изменениям в вычислительной сложности получения решения.
После вставка операций прореживания в backtracking алгоритм и в решении beltway проблемы выявился полный аналог того, о чем говорила Тамара Дакис относительно turnpike проблемы. Напомню. Она говорила, что для turnpike проблемы возможно получить решение за полиномиальное время, если решение единственно и отсутствует дублирование в $inline$\Delta X$inline$. Оказалось, что не обязательно нужно полное отсутствие дублирования (вряд ли оно возможно для реальных данных), достаточно, что его уровень будет достаточно малым. На рисунке ниже показано, сколько времени требуется для получения решения beltway проблемы в зависимости от длины пептида и уровня дублирования в $inline$\Delta X$inline$.

На рисунке обе оси абсцисс и ординат даны в логарифмическом масштабе. Это позволяет четко увидеть является ли зависимость времени счета от длины последовательности $inline$T = f (n)$inline$ экспоненциальной (прямая линия) или полиномиальной (log-форма кривой). Как видно на диаграммах, при низком уровне дублирования (правая диаграмма) решение получается в полиномиальное время. Ну, а если быть более точным, то решение получается за квадратичное время. Это происходит, когда операции прореживания снижают мощность множества до нижнего предела $inline$O (n^2) \rightarrow O (n)$inline$, в нем остается мало точек, возвраты при переборе вариантов становятся единичными, и по сути алгоритм перестает перебирать варианты, а просто конструирует решение из того, что осталось.
P.S. Ну и раскрою последний секрет относительно генерации множеств в разным уровнем дублирования. Это связано с разной точностью представления данных. Если данные генерятся с низкой точностью (например округляя до целых чисел), то уровень дублирования становится высоким, более 0.3. Если данные генерить с хорошей точностью, например, до 3 знака после запятой, то уровень дублирования резко снижается, менее 0.1. И отсюда следует последнее наиболее важное замечание.
Для реальных данных, в условиях постоянно увеличивающейся точности измерений, beltway проблема становится разрешима в реальном времени.
Литература.
1. Dakic, T. (2000). On the Turnpike Problem. PhD thesis, Simon Fraser University.
2. Fomin. E. (2016a) A Simple Approach to the Reconstruction of a Set of Points from the Multiset of n^2 Pairwise Distances in n^2 Steps for the Sequencing Problem: I. Theory. J Comput Biol. 2016, 23(9):769–75.
3. Fomin. E. (2016b) A Simple Approach to the Reconstruction of a Set of Points from the Multiset of n^2 Pairwise Distances in n^2 Steps for the Sequencing Problem: II. Algorithm. J Comput Biol. 2016, 23(12):934–942.
4. Lemke, P., Skiena, S., and Smith, W. (2003). Reconstructing Sets From Interpoint Distances. Discrete and Computational Geometry Algorithms and Combinatorics, 25:597–631.
5. Skiena, S., Smith, W., and Lemke, P. (1990). Reconstructing sets from interpoint distances. In Proceedings of the Sixth ACM Symposium on Computational Geometry, pages 332–339. Berkeley, CA
6. Zhang, Z. 1982. An exponential example for a partial digest mapping algorithm. J. Comp. Biol. 1, 235–240.
