[Из песочницы] Методы имитационного моделирования вероятностных распределений на языке программирования Python
В данной статье рассмотрим методы имитационного моделирования на основе теории систем массового обслуживания, в которых широко используются элементы математической статистики и теории вероятностей. Целью данной статьи является разработка методов, которые можно использовать для создания моделей, в основе которых фигурируют вероятностные распределения и элементы массового обслуживая.
Прежде, чем приступить к разработке методов, определим ключевые подходы, которые мы будем использовать в процессе: генерация случайных величин, вероятностные распределения, а также некоторые элементы теории вероятностей и математической статистики. В результатах опытов увидим экспериментальную демонстрацию поведения вероятностных распределений и имитации случайных процессов. Всё это и даст нам инструментальную основу для создания различных имитационных моделей, в которых фигурируют вероятностные распределения.
Все методы моделирования данного исследования представлены на программном языке Python. Этот язык является распространённым инструментов в сфере научных исследований и сфере обучения.
В дальнейших этапах исследования, которые будут представлены в будущих статьях, перейдём к более сложным экспериментам: рассмотрим вероятностные распределения, которые не вошли рамки данной статьи, рассмотрим имитационное моделирования систем и сетей массового обслуживания, и также продемонстрируем программирование подобных моделей с использованием параллельных вычислений.
Методы моделирование случайных величин и генераторы случайных чисел python
Рассмотрим простые модели подбрасывания одного или нескольких игральных кубиков. Моделирование начнём с генерации случайных чисел. Задача генерации чисел и вопросы об истинной и квази-случайности в наши исследования не входят, но Вы можете найти данные обсуждения в других источниках. В наших моделях используется генератор псевдо-случайных величин Python. На начальном этапе, для наглядности изучения, можно повышать количество испытаний, наблюдая результат моделирования.
Начнём с генерации случайных величин. Методы их генерирования сводятся к использованию стандартных библиотек Python.
Модуль random из стандартной библиотеки предоставляет возможность получения случайных вещественных чисел в диапазоне от 0 до 1, случайных целых чисел в заданном диапазоне, случайного выбора элементов последовательности и многое другое:
Модуль random может использоваться, например, для перемешивания колоды карт в игре, случайного выбора изображения в программе демонстрации слайдов, в программах статистического моделирования и так далее. За дополнительной информацией обращайтесь к руководству по стандартной библиотеке языка Python.
Расширение NumPy, содержащее реализацию математических вычислений для Python благодаря комбинированию компилированных и оптимизированных библиотек расширения с языком Python NumPy превращает Python в мощный, эффективный и удобный инструмент математических вычислений.
Подробное описание модуля NumPy вы найдёте в официальной документации по этому пакету.
Методы моделирование вероятностных распределений с помощью python
Приступим к моделированию: будем подбрасывать игральный кубик. Ниже представлен листинг программирования модели подбрасывания одного кубика (рис. 1). Кубик может принимать одно из шести значений.
import pylab
import numpy
# Количество испытаний
trials = 500
# Массив значений
values = numpy.random.randint(1, 7, size=trials)
pylab.hist(values, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5], edgecolor='white')
pylab.xlabel('Значение')
pylab.ylabel('Количества раз')
pylab.title('Подбрасывание кубика ' + str(trials) + ' раз')
pylab.show()
Рис. 1. Листинг программирования модели подбрасывания одного кубика
В представленной программе задаём количество испытаний: сколько раз подбрасывается кубик, и массив: какое значение выпадает в каждом испытании. Результат выводим в виде гистограммы (рис. 2).
Рассматривая результат, можно предположить, что распределение имеет равномерный характер. Увеличив число испытаний до 10 000 раз можно увидеть, что гистограмма имеет вид, подобный гистограмме равномерного распределения.
Следующим испытанием рассмотрим модель подбрасывания двух игральных кубиков. Код программы при этом незначительно измениться (рис. 3).

Рис. 2. Результаты моделирования подбрасывания одного кубика
...
# Массив значений
values = []
for i in range(trials):
values.append(numpy.random.randint(1, 7) + numpy.random.randint(1, 7))
pylab.hist(values, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5,
7.5, 8.5, 9.5, 10.5, 11.5, 12.5, 13.5],
facecolor='green', edgecolor='white')
...
Рис. 3. Часть изменённого листинга для программирования модели подбрасывания двух кубиков
В представленном листинге значительным изменением является присвоение значения массиву, в который записываем выпавшие значения уже двух кубиков. Вторым изменением, менее значительным, является представления гистограммы соответствующих вариантов значений. Результат выполнения программы представлен на рис. 4.
Получив результат моделирования подбрасывания двух кубиков рассмотрим задачу моделирования нормального (Гаусс) распределения и насколько она коррелирует с задачей моделирования подбрасывания нескольких кубиков. Код программы также меняется незначительно: меняется всего одна строка присваивания значений массиву (рис. 5).
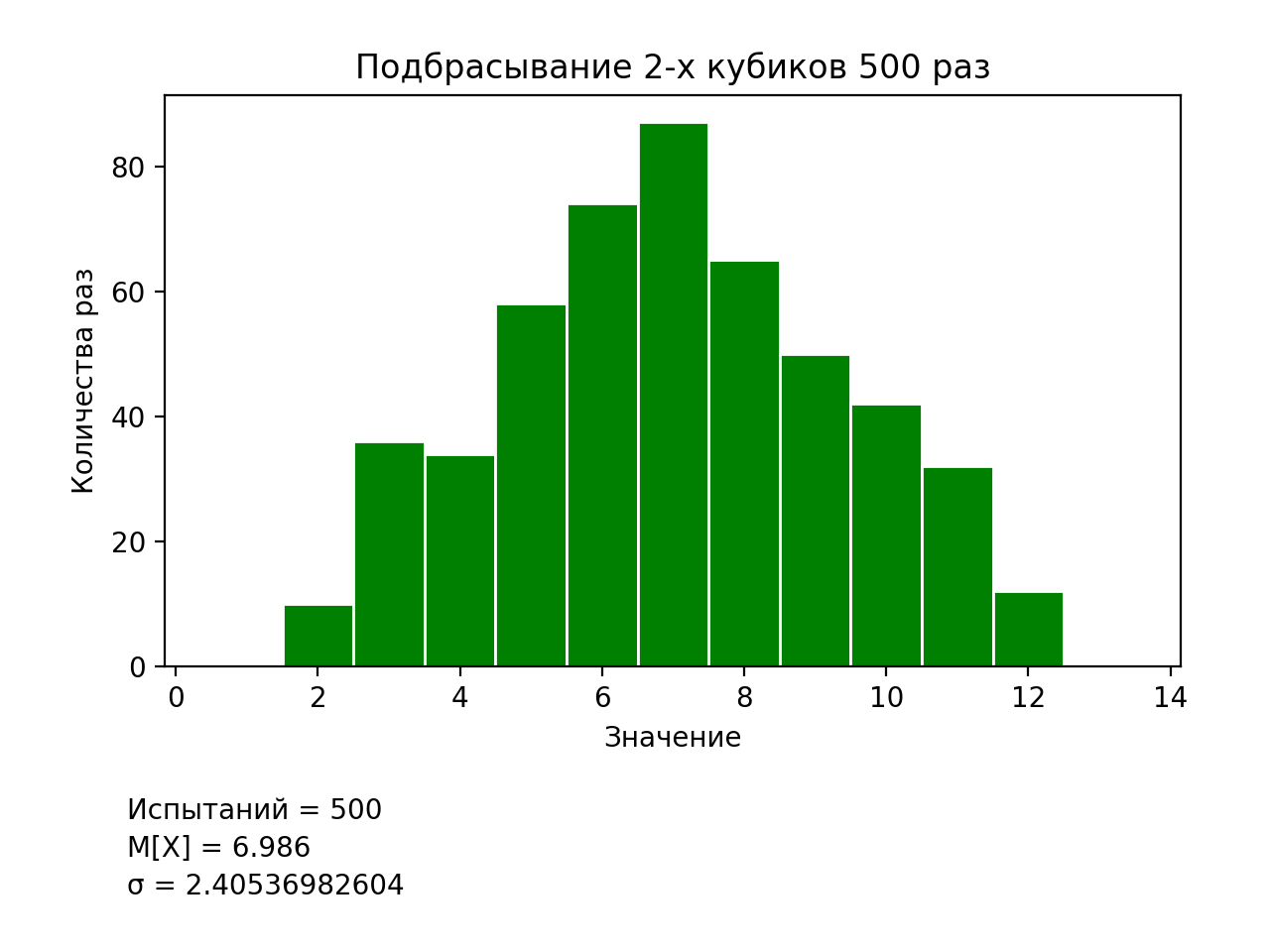
Рис. 4. Результаты моделирования подбрасывания двух кубиков
...
# Массив значений
values = []
for i in range(trials):
mu = 7
sigma = 2.4
values.append(random.normalvariate(mu, sigma))
...
Рис. 5. Часть изменённого листинга для программирования модели нормального распределения
На представленном листинге используется метод normalvariate библиотеки random, генерирующий величины с нормальным вероятностным распределением со параметрами mu и sigma, которые являются среднем значением и стандартным отклонением распределения соответственно. Результат выполнения программы представлен на рис. 6.
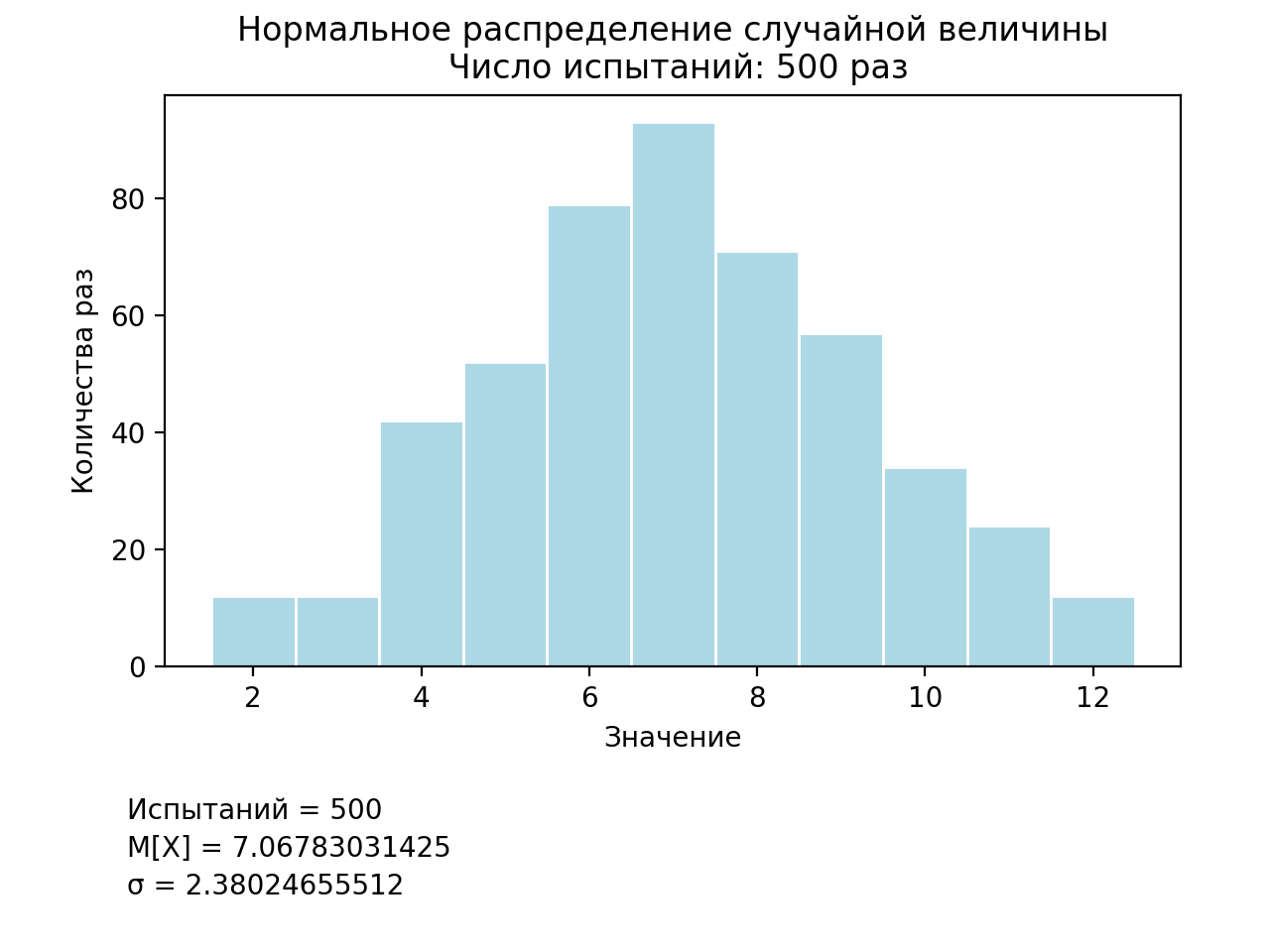
Рис. 6. Результаты моделирования нормального распределения
Заключительным этапом является моделирование экспоненциального распределения. Экспоненциальное распределение часто используется при моделировании распределения (длительности) интервалов между моментами поступления заявок в системах массового обслуживания разного типа. Листинг также отличается незначительно от остальных листингов программ, представленных в нашем исследовании (рис. 7).
Результат моделирования представлен на рис. 8.
...
lambd = 10
# Массив значений
values = []
for i in range(trials):
values.append(random.expovariate(lambd))
pylab.hist(values, 20, facecolor='lightgreen', edgecolor='white')
...
Рис. 7. Часть изменённого листинга для программирования модели экспоненциального распределения
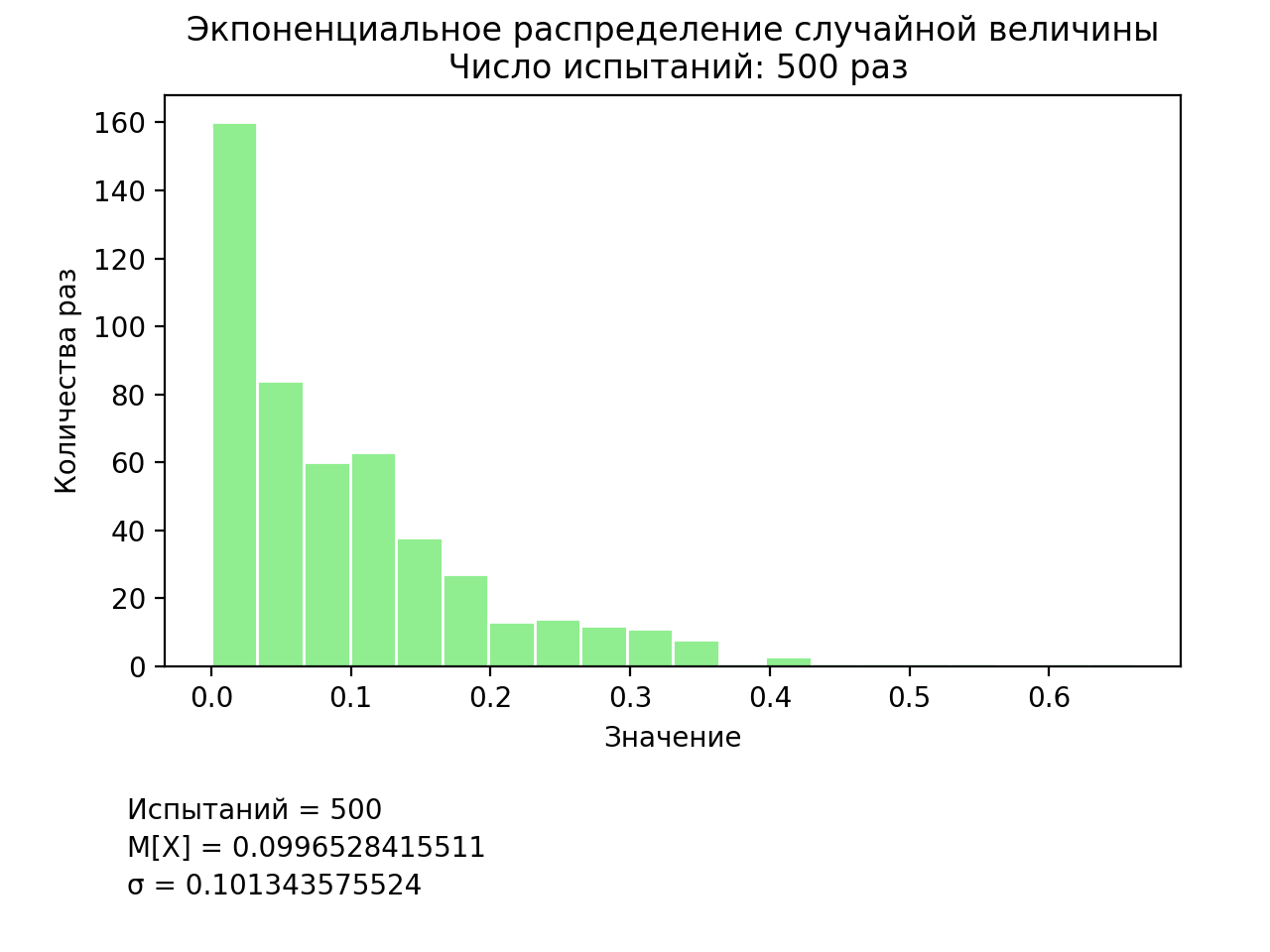
Рис. 8. Результаты моделирования экспоненциального распределения
Заключение
В этой статье были рассмотрены несколько программных реализаций моделей вероятностных распределений на языке Python. Эти модели дают основу для проведения собственных экспериментов и исследований.
На данном этапе представлены только некоторые методы и подходы, и в дальнейшем, автор представит дополнительные методы для моделирования с использованием вероятностных распределений, языка программирования Python и теории массового обслуживания.
