[Из песочницы] Методика создания образов на примере Docker

Пришло время разложить информацию о контейнерах «по полочкам» в голове в статье и формализовать подход к построению образов Docker. Еще при первом знакомстве с Docker все запущенные контейнеры напоминали костыли и велосипеды избыточные наборы файлов, библиотек, поверх которых запускались процессы. Что бы такого не было, хотелось объединить дублирующие слои в один, но в то же время предоставить каждому исполняемому файлу свой контейнер. Так постепенно начал формироваться свой подход к построению образов. Но чем же плохи «костыли и велосипеды»? Ответ один — они могут появиться в конечном продукте.
На самом деле, если разработчику не хочется в будущем что-то менять в запущенном контейнере, который собирался временно или только для тестирования, нет необходимости в продумывании структуры образов, его слоев и размера. В готовом же продукте каждый избыточный слой выливается в лишние мегабайты информации, которую приходится скачивать или через медленное подключение к Docker Hub, либо перекидывать сжатыми файлами. А когда приходится обновлять версию продукта, то полезнее заменять какой-то образ и зависимый от него один контейнер, чем всю систему. В этом случае и возникают мысли как лучше собрать образ для контейнера, чтобы его удобно было использовать в «продакшен», своевременно обновить продукт и облегчить жизнь при развертывании его в кластере.
Для начала определимся — что такое слой образа. Если максимально подробно расписывать Doсkerfile, то каждый новый слой будет представлять из себя добавляемый или модифицируемый файл (даже если это переменная окружения внутри будущего контейнера).
Теперь представим такие файлы, как — как множество однотипных элементов Q. Также определим все процессы или контейнеры, которые будут существовать в нашей системе, составим множество X. Каждому такому процессу соответствует какой-то исполняемый файл, который в свою очередь зависит от других элементов файловой системы. Будем считать такие множества A, B, C, D и E проекциями процессов (элементов множества X) на множестве Q.

Представим зависимости между файлами (библиотеками и т. п.) в виде линий над элементами, получим множества A (a1-a2, a2-a3, a3-a4), B (b1-b2), C (c1-c2, c2-c3, c3-c4, c5-c6, c6-c4), D (d1-d2, d2-d3, d3-d4, d5-d6, d6-d4, d7-d4). Справа показаны процессы из множества Х, слева соответствующие им исполняемые файлы (a4, b2, c4, d4, e1) и их зависимости. Для исполняемых файлов определяем библиотеки, переменные окружения, устройства и отражаем в виде соответствующих элементов. Так как у каждого процесса не существует более одного исполняемого файла, то эти элементы будут являться ключевыми при создании контейнера. Дополнительно хотелось бы отметить, что нет необходимости подробно описывать каждый файл. Достаточно лишь описать утилиту, если ее библиотеки нигде больше не используются и, например, считать утилиту curl, как один элемент.
В соответствии с теми условиями, что определили вначале статьи для конечного продукта, компонуем все элементы множества Q в контейнеры и шаблоны. Для каждого отражения определим общие элементы (узлы), присутствующие одновременно в нескольких множествах, промаркируем их Q (q1)=A (a1)=C (c1)=D (d1), Q (q2)=A (a3)=B (b1), Q (3)=C (c5)=D (d5), Q (4)=C (c6)=D (d6) и установим соответствующие зависимости, пренебрегая отдельными элементами.
В дальнейшем будем работать с этими элементами и на их основе компоновать шаблоны контейнеров. Так как элементы в каждом множестве будут постоянно изменяться (некоторые элементы чаще, другие реже), необходимо выделить их особым образом. Для этого найдем самую длинную цепочку по зависимостям среди множеств, начиная с элемента, соответствующего исполняемому файлу, например a1-a2-a3-a4. Количество узлов в такой цепочке будет соответствовать максимальной степени обновления элементов в множестве, т. е. равна четырем. Будем считать, что при степени равной одному данный элемент в системе не обновляется или изменяется очень редко, вследствие чего его выделяем в отдельный шаблон. При максимальной степени этот элемент будет постоянно меняться, и его следует выделить уже в контейнере.
Так как отображение каждого процесса представляет собой множество зависящих между собой элементов, то данную структуру также необходимо проиндексировать. Узловые элементы присутствуют во всех множествах, они индексируются для каждого набора отдельно. Например: A (a1=1, a2=2, a3=3, a4=4), B (b1=2, b2=3), C (c1=1, c2=2, c3=2, c4=3, c5=2, c6=2), D (d1=2, d2=2, d3=3, d4=4, d5=2, d6=3), E (e1=3). Итоговой степенью обновления узлового элемента будет являться максимальный индекс среди всех множеств. Получаем: q1=2, q2=3, q3=2, q4=3.
Следует учесть, что узловые элементы не могут образовываться двумя одинаковыми шаблонами, так как по определению каждый контейнер строится только на одном шаблоне. Из этого следует, что все зависимости элементов с одинаковой степенью необходимо включить в один шаблон.

Данную операцию следует повторять несколько раз, так как вследствие объединения появляются новые зависимости.
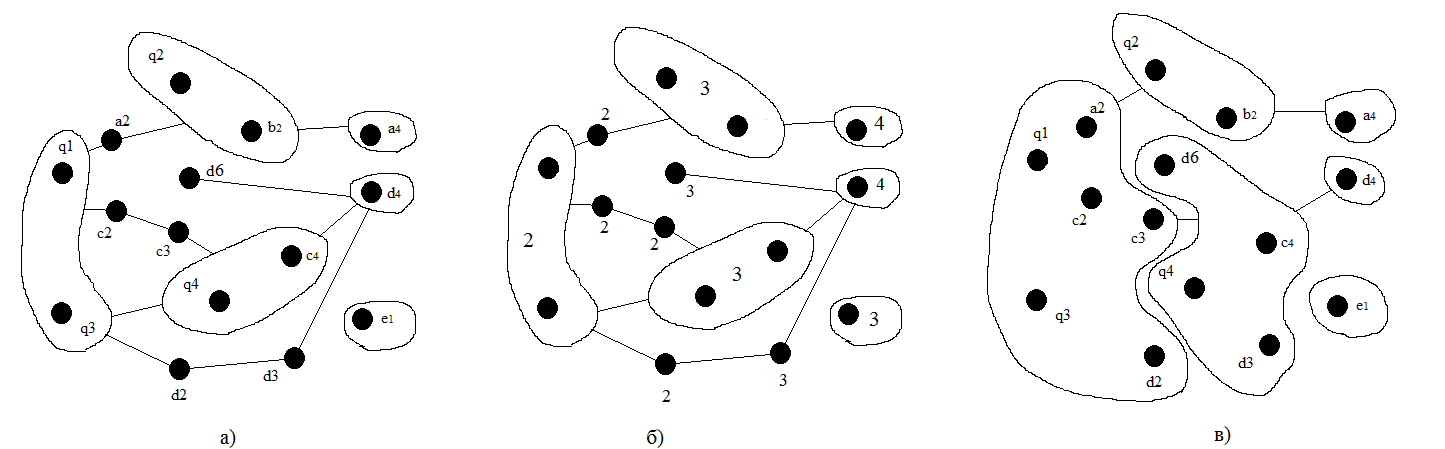
В последнюю очередь необходимо выделить все элементы, от которых зависят шаблоны, и объединить их либо в один (если их индексы соответствуют), либо с шаблоном, который от них зависит. В получившейся структуре отражены взаимосвязи, при образовании которых учитывалась степень обновления элементов и их зависимости. В получившейся структуре отражены взаимосвязи, при образовании которых учитывалась степень обновления элементов и их зависимости.
Окончательную структуру получившихся образов и контейнеров можно увидеть на рисунке:

Итогом данной статьи является подход к формированию образов Docker, когда вся используемая файловая система разбивается на элементы. Эти элементы маркируются в зависимости от частоты их обновления в конечном продукте или на этапе разработки. И далее объединяются в логически завершенные образы, на основе которых запускаются контейнеры.
PS: Прошу простить из-за возможных ошибок в статье и немного сумбурном изложении, но думаю смысл статьи можно уловить, просто посмотрев картинки и прочитав вывод.
