[Из песочницы] Линейная регрессия и градиентный спуск
Пусть в некоторой предметной области исследуются показатели X и Y, которые имеют количественное выражение.
При этом есть все основания полагать, что показатель Y зависит от показателя X. Это положение может быть как научной гипотезой, так и основываться на элементарном здравом смысле. К примеру, возьмем продовольственные магазины.
Обозначим через:
X — торговую площадь (кв. м.)
Y — годовой товарооборот (млн. р.)
Очевидно, что чем выше торговая площадь, тем выше годовой товарооборот (предполагаем линейную зависимость).
Представим, что у нас есть данные о некоторых n магазинах (торговая площадь и годовой товарооборот) — наш датасет и k торговых площадей (X), для которых мы хотим предсказать годовой товарооборот (Y) — наша задача.
Выдвинем гипотезу, что наше значение Y зависит от X в виде: Y = a + b * X
Чтобы решить нашу задачу, мы должны подобрать коэффициенты a и b.
Для начала зададим a и b случайные значения. После этого нам нужно определиться с функцией потерь и оптимизационным алгоритмом.
Для этого мы можем воспользоваться среднеквадратичной функцией потерь (MSELoss). Вычисляется по формуле:
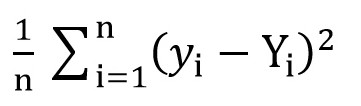
Где y[i] = a + b * x[i] после a = rand () и b = rand (), а Y[i] — правильное значение для x[i].
На данном этапе мы имеем среднеквадратичное отклонение (некую функцию от a и b). И очевидно, что, чем меньше значение этой функции, тем более точно подобраны параметры a и b относительно тех параметров, которые описывают точную зависимость между площадью торгового помещения и товарооборотом в этом помещении.
Теперь мы можем приступить к использованию градиентного спуска (как раз для минимизации функции потерь).
Градиентный спуск
Суть его очень проста. Например, мы имеем функцию:
y = x*x + 4 * x + 3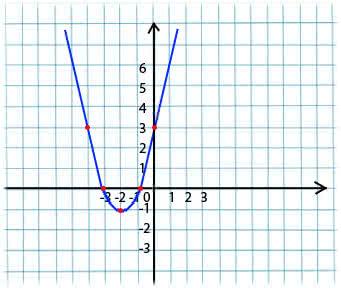
Берем произвольное значение x из области определения функции. Представим, что это точка x1 = -4.
Далее мы берем производную по x от этой функции в точке x1(если функция зависит от нескольких переменных (например, от a и b), то нужно брать частные производные по каждой из переменных). y»(x1) = -4 < 0
Теперь получаем новое значение для x: x2 = x1 — lr * y»(x1). Параметр lr (learning rate) позволяет устанавливать размер шага. Таким образом получаем:
Если частная производная в заданной точке x1 < 0 (функция убывает), то мы движемся к точке локального минимума. (x2 будет больше, чем x1)
Если частная производная в заданной точке x1 > 0 (функция возрастает), то мы все по-прежнему движемся к точке локального минимума. (x2 будет меньше, чем x1)
Выполняя этот алгоритм итерационно, мы приблизимся к минимуму (но не достигнем его).
На практике это все выглядит куда более просто (однако я не берусь утверждать, какие коэффициенты a и b подойдут максимально точно к вышеописанному случаю с магазинами, поэтому возьмем зависимость вида y = 1 + 2 * x для генерации датасета, а потом обучим нашу модель на этом датасете):
(Код написан здесь)
import numpy as np
# инициализация повторяемой последовательности случайных чисел
np.random.seed(42)
# создаём np-массив из 1000 случайных чисел в диапазоне 0..1
sz = 1000
x = np.random.rand(sz, 1)
# строим функцию y = f(x) и добавляем немного гауссова шума
y = 1 + 2 * x + 0.1 * np.random.randn(sz, 1)
# формируем индексы от 0 до 999
idx = np.arange(sz)
# случайно их тасуем
np.random.shuffle(idx)
train_idx = idx
# формируем наборы обучающих данных
x_train, y_train = x[train_idx], y[train_idx]
# задаём начальные случайные значения коэффициентам линейной регрессии
a = np.random.randn(1)
b = np.random.randn(1)
print(a,b)
# скорость обучения
lr = 0.01
# количество эпох
n_epochs = 10000
# основной цикл
for epoch in range(n_epochs):
# рассчитываем результирующий массив с текущими коэффициентами a и b
# на основе обучающей выборки
yhat = a + b * x_train
# 1. определяем лосс
# считаем отклонение нового результата от обучающего:
error = (y_train - yhat)
# 2. считаем градиенты (вспоминая формулу производной)
# для коэффициента a
a_grad = -2 * error.mean()
# для коэффициента b
b_grad = -2 * (x_train * error).mean()
# 3. обновляем параметры, используя коэффициент скорости обучения
a = a - lr * a_grad
b = b - lr * b_grad
print(a,b)
Скомпилировав код, можно заметить, что начальные значения a и b были далеки от требуемых 1 и 2 соответсвенно, а итоговые значения весьма близки.
Немного проясню моменты того, почему у нас a_grad и b_grad считаются именно так.F(a, b) = (y_train - yhat) ^ 2 = (1 + 2 * x_train – a + b * x_train). Частная производная F по a будет равняться -2 * (1 + 2 * x_train – a + b * x_train) = -2 * error. Частная производная F по b будет равняться -2 * x_train * (1 + 2 * x_train – a + b * x_train) = -2 * x_train * error. Мы берем среднее значение (mean()) в виду того, что error и x_train, и y_train — это массивы значений, a и b — это скаляры.
Материалы, используемые в статье:
towardsdatascience.com/understanding-pytorch-with-an-example-a-step-by-step-tutorial-81fc5f8c4e8e
www.mathprofi.ru/metod_naimenshih_kvadratov.html
