[Из песочницы] Криптографический алгоритм «Кузнечик»: просто о сложном
В данной статье будет подробно рассмотрен алгоритм блочного шифрования, определенный в ГОСТ Р 34.12–2015 как «Кузнечик». На чем он основывается, какова математика блочных криптоалгоритмов, а так же как реализуется данный алгоритм в java.
Кто, как, когда и зачем разработал данный алгоритм останется за рамками статьи, так как в данном случае нас это мало интересует, разве что:
КУЗНЕЧИК = КУЗнецов, НЕЧаев И Компания.

Так как криптография в первую очередь основана на математике, то чтобы дальнейшее объяснение не вызвало уймы вопросов сначала стоит разобрать базовые понятия и математические функции, на которых строится данный алгоритм.
Поля Галуа
Арифметика полей Галуа — полиномиальная арифметика, то есть каждый элемент данного поля представляет собой некий полином. Результат любой операции также является элементом данного поля. Конкретное поле Галуа состоит из фиксированного диапазона чисел. Характеристикой поля называют некоторое простое число p. Порядок поля, т.е. количество его элементов, является некоторой натуральной степенью характеристики pm, где m ϵ N. При m=1 поле называется простым. В случаях, когда m>1, для образования поля необходим еще порождающий полином степени m, такое поле называется расширенным. $inline$GF (p^m) $inline$ — обозначение поля Галуа. Порождающий полином является неприводимым, то есть простым (по аналогии с простыми числами делится без остатка на 1 и на самого себя). Так как работа с любой информацией — это работа с байтами, а байт представляет из себя 8 бит, в качестве поля берут $inline$GF (2^8)$inline$ и порождающий полином:
$$display$$x^8 + x^7 + x^6+x+1.$$display$$
Однако для начала разберем основные операции в более простом поле $inline$GF (2^3)$inline$ с порождающим полиномом $inline$f (x)=x^3+x+1$inline$.
Операция сложения
Самой простой является операция сложения, которая в арифметике полей Галуа является простым побитовым сложением по модулю 2 (ХОR).
Сразу обращаю внимание, что знак »+» здесь и далее по тексту обозначает операцию побитового XOR, а не сложение в привычном виде.
Таблица истинности функции ХОR
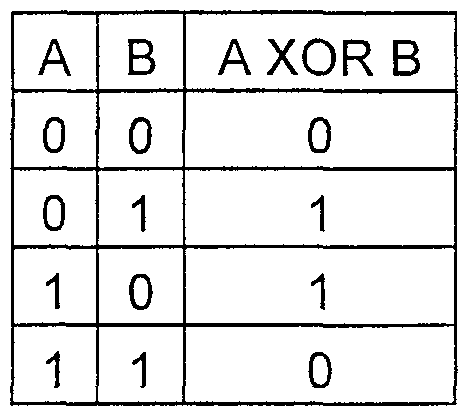
Пример: $inline$5 + 3 = 101 + 011 = 110_2 = 6_{10}$inline$
В полиномиальном виде данная операция будет выглядеть как
$$display$$(x^2 + 1) + (x + 1) = x^2 + x = 110_2 = 6_{10}$$display$$
Операция умножения
Чтобы осуществить операцию умножения, необходимо преобразовать числа в полиномиальную форму:
$$display$$5 = 101_2 =1*x^2 +0*x^1+1*x^0=x^2 + 1$$display$$
Как можно заметить число в полиномиальной форме представляет собой многочлен, коэффициентами которого являются значения разрядов в двоичном представлении числа.
Перемножим два числа в полиномиальной форме:
$$display$$5×7=(x^2+1)*(x^2+x+1)=x^4+x^3+x^2+x^2+x+1=$$display$$
$$display$$=x^4+x^3+x+1=11011_2=27_{10}$$display$$
Результат умножения 27 не входит в используемое поле $inline$GF (2^3)$inline$ (оно состоит из чисел от 0 до 7, как было сказано выше). Чтобы бороться с этой проблемой, необходимо использовать порождающий полином.
Также предполагается, что x удовлетворяет уравнению $inline$f (x)=x^3+x+1=0$inline$, тогда

Составим таблицу умножения:
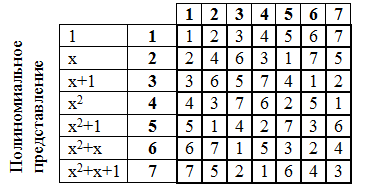
Большое значение имеет таблица степеней элементов поля Галуа. Возведение в степень также осуществляется в полиномиальной форме, аналогично умножению.
Пример:
$$display$$5^2=(x^2+1)^2=x^4+x^2+x^2+1=x^4+x^2+x+x^2+x+1=$$display$$
$$display$$=x (x^3+x+1)+x^2+x+1=x^2+x+1=111_2=7_{10}$$display$$
Таким образом, составим таблицу степеней:

Таблица степеней обладает цикличностью: седьмая степень соответствует нулевой, значит восьмая соответствует первой и т.д. При желании можно это проверить.
В полях Галуа существует понятие примитивного члена — элемент поля, чьи степени содержать все ненулевые элементы поля. Просмотрев таблицу степеней видно, что этому условию соответствуют все элементы (ну кроме 1 естественно). Однако это выполняется не всегда.
Для полей, которые мы рассматриваем, то есть с характеристикой 2, в качестве примитивного члена всегда выбирают 2. Учитывая его свойство, любой элемент поля можно выразить через степень примитивного члена.
Пример:$inline$5=2^6,7=2^5$inline$
Воспользовавшись этим свойством, и учитывая цикличность таблицы степеней, попробуем снова перемножить числа:
$$display$$5×7=2^6×2^5=2^{(6+5)}=2^{(11mod7)}=2^4=6$$display$$
Результат совпал с тем, что мы вычислили раньше.
А теперь выполним деление:
$$display$$6/5=2^4/2^6=2^{(4–6)}=2^{((-2)mod7)}=2^5=7$$display$$
Полученный результат тоже соответствует действительности.
Ну и для полноты картины посмотрим на возведение в степень:
$$display$$5^2=(2^6)^2=2^{(6×2)}=2^{(12mod7)}=2^5=7$$display$$
Такой подход к умножению и делению гораздо проще, чем реальные операции с использование полиномов, и для них нет необходимости хранить большую таблицу умножения, а достаточно лишь строки степеней примитивного члена поля.
Теперь вернемся к нашему полю $inline$GF (2^8)$inline$
Нулевой элемент поля — это единица, 1-ый — двойка, каждый последующий со 2-ого по 254-ый элемент вычисляется как предыдущий умноженный на 2, а если элемент выходит за рамки поля, то есть его значение больше чем $inline$(2^8–1)$inline$, то делается XOR с числом $inline$195_{10}$inline$, это число представляет неприводимый полином поля $inline$x^8 + x^7 + x^6+x+1=2^8 + 2^7 ++ 2^6+2+1=451$inline$, приведем это число в рамки поля $inline$451–256=195$inline$. А 255-ый элемент снова равен 1. Таким образом у нас есть поле, содержащее 256 элементов, то есть полный набор байт и мы разобрали основные операции, которые выполняются в этом поле.
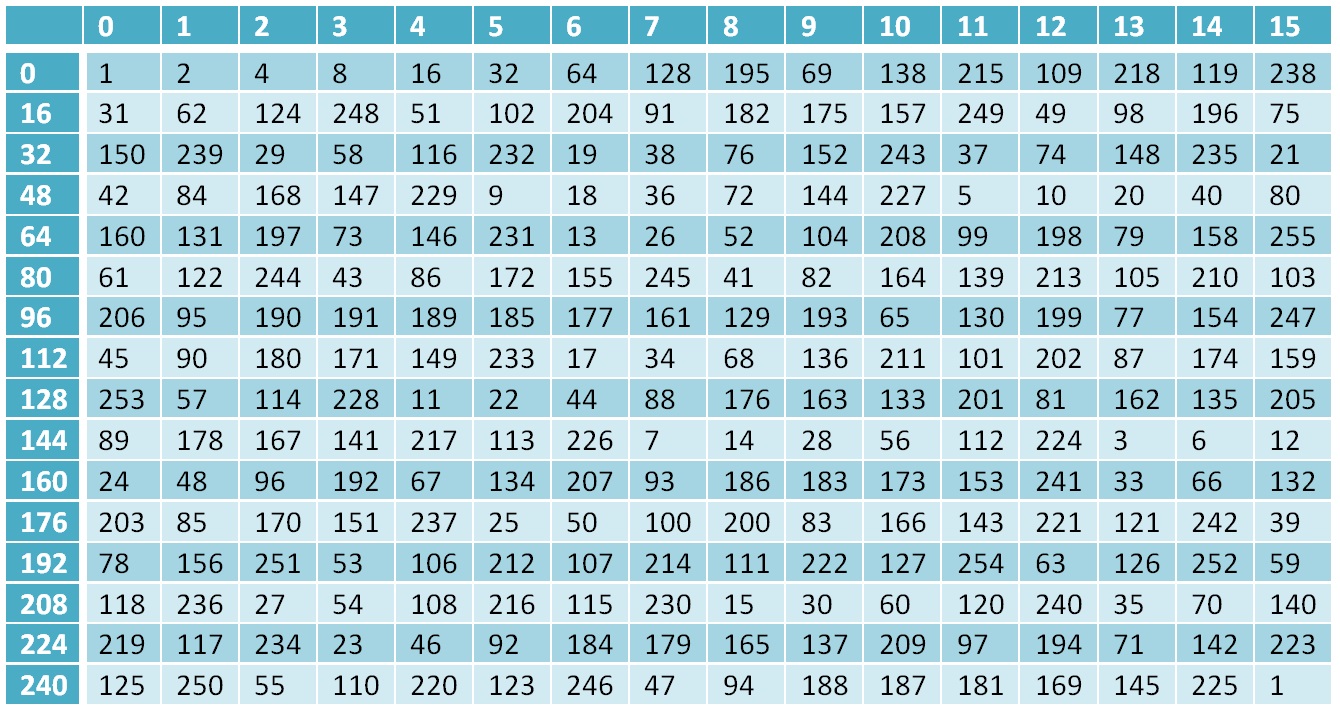
Таблица степеней двойки для поля $inline$GF (2^8)$inline$
Для чего это было нужно — часть вычислений в алгоритме Кузнечик выполняются в поле Галуа, а результаты вычислений соответственно являются элементами данного поля.
Сеть Фейстеля
Сеть Фейстеля —это метод блочного шифрования, разработанный Хорстом Фейстелем в лаборатории IBM в 1971 году. Сегодня сеть Фейстеля лежит в основе большого количества криптографических протоколов.
Сеть Фейстеля оперирует блоками открытого текста:
- Блок разбивается на две равные части — левую L и правую R.
- Левый подблок L изменяется функцией f с использованием ключа K: X = f (L, K). В качестве функции может быть любое преобразование.
- Полученный подблок X складывается по модулю 2 с правым подблоком R, который остался без изменений: X = X + R.
- Полученные части меняются местами и склеиваются.
Эта последовательность действий называется ячейкой Фейстеля.

Рисунок 1. Ячейка Фейстеля
Сеть Фейстеля состоит из нескольких ячеек. Полученные на выходе первой ячейки подблоки поступают на вход второй ячейки, результирующие подблоки из второй ячейки попадают на вход третьей ячейки и так далее.
Алгоритм шифрования
Теперь мы познакомились с используемыми операциями и можем перейти к основной теме —, а именно криптоалгоритму Кузнечик.
Основу алгоритма составляет так называемая SP сеть — подстановочно-перестановочная сеть (Substitution-Permutationnetwork). Шифр на основе SP-сети получает на вход блок и ключ и совершает несколько чередующихся раундов, состоящих из стадий подстановки и стадий перестановки. В «Кузнечике» выполняется девять полных раундов, каждый из которых включает в себя три последовательные операции:
- Операция наложения раундового ключа или побитовый XOR ключа и входного блока данных;
- Нелинейное преобразование, которое представляет собой простую замену одного байта на другой в соответствии с таблицей;
- Линейное преобразование. Каждый байт из блока умножается в поле Галуа на один из коэффициентов ряда (148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1) в зависимости от порядкового номера байта (ряд представлен для порядковых номеров от 15-ого до 0-ого, как представлено на рисунке). Байты складываются между собой по модулю 2, и все 16 байт блока сдвигаются в сторону младшего разряда, а полученное число записывается на место считанного байта.

Последний десятый раунд не полный, он включает в себя только первую операцию XOR.
Кузнечик — блочный алгоритм, он работает с блоками данных длинной 128 бит или 16 байт. Длина ключа составляет 256 бит (32 байта).

Рисунок 2. Схема шифрования и расшифрования блока данных
На схеме показана последовательность операций, где S — нелинейное преобразование, L — линейное преобразование, Ki — раундовые ключи. Сразу возникает вопрос — откуда берутся раундовые ключи.
Формирование раундовых ключей
Итерационные (или раундовые) ключи получаются путем определенных преобразований на основе мастер-ключа, длина которого, как мы уже знаем, составляет 256 бит. Этот процесс начинается с разбиения мастер-ключа пополам, так получается первая пара раундовых ключей. Для генерации каждой последующей пары раундовых ключей применяется восемь итераций сети Фейстеля, в каждой итерации используется константа, которая вычисляется путем применения линейного преобразования алгоритма к значению номера итерации.

Схема получения итерационных (раундовых) ключей
Если вспомнить рисунок 1, то левый подблок L — левая половина исходного ключа, правый подблок R — правая половина исходного ключа, K — константа Ci, функция f — последовательность операций R XOR Ci, нелинейное преобразование, линейное преобразование.
Итерационные константы Ci получаются с помощью L-преобразования порядкового номера итерации.
Значит чтобы осуществить шифрование блока текста нам надо сначала рассчитать 32 итерационные константы, затем на основе ключа вычислить 10 раундовых ключей, и потом выполнить последовательность операций, представленных на рисунке 2.
Давайте начнем с вычисления констант:
Первая констант $inline$C_1 = 1_{10} = 00000001_2 = 01_{16}$inline$, однако все преобразования в нашем алгоритме выполняются с блоками длиной 16 байт, поэтому необходимо дополнить константу до длины блока, то есть дописать справа 15 нулевых байт, получим
$$display$$C_1 = 01000000000000000000000000000000$$display$$
Умножим ее на ряд (1, 148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148) следующим образом:
$$display$$a_{15}=a_{15}*148+a_{14}*32+a_{13}*133+a_{12}*16+$$display$$
$$display$$+a_{11}*194+a_{10}*192+a_9×1+a_8×251+a_7×1+a_6×192+$$display$$
$$display$$+a_5×194+a_4×16+a_3×133+a_2×32+a_1×148+a_0×1$$display$$
(данное равенство приведено в операциях полей Галуа)
Так как все кроме нулевого байта равны 0, а нулевой байт умножается на 1, то получим 1 и запишем его в старший разряд числа, сдвинув все байты в сторону младшего разряда, получим:
$$display$$C_1 = 00000000000000000000000000000001$$display$$
Повторим те же операции. На этот раз $inline$a_{15}=1$inline$, все остальные байты 0, следовательно из слагаемых остается только первое $inline$ a_{15}*148=1×148=148_{10}=94_{16}$inline$, получаем:
$$display$$C_1 = 00000000000000000000000000000194$$display$$
Делаем третью итерацию, здесь два ненулевых слагаемых:
$$display$$a_{15}*148+a_{14}*32=148×148+1×32=$$display$$
$$display$$=10010100×10010100+00000001×00100000=$$display$$
$$display$$=(x^7+x^4+x^2)*(x^7+x^4+x^2)+1*x^5=x^{14}+x^8+x^4+x^5=$$display$$
$$display$$=x^6 (x^8+x^7+x^6+x+1)+x^{13}+x^{12}+x^7+x^6+x^8+x^4+x^5=$$display$$
$$display$$=x^5 (x^8+x^7+x^6+x+1)+x^{11}+x^5+x^7+x^8+x^4+x^5=$$display$$
$$display$$=x^3 (x^8+x^7+x^6+x+1)+x^{10}+x^9+x^3+x^8+x^7=$$display$$
$$display$$=x^2 (x^8+x^7+x^6+x+1)+x^2+x^7=x^7+x^2=132_{10}$$display$$
$$display$$132_{10}=84_{16}$$display$$
По таблице степеней можно было решить это гораздо проще:
$$display$$148×148+1×32=2^{45}*2^{45}+2^5=2^{90}+2^5=164+32=132$$display$$
$$display$$C_1 = 00000000000000000000000000019484$$display$$
Далее все точно также, всего 16 итераций на каждую константу
$$display$$C_1 = 000000000000000000000000019484DD$$display$$
$$display$$C_1 = 0000000000000000000000019484DD10$$display$$
$$display$$C_1 = 00000000000000000000019484DD10BD$$display$$
$$display$$C_1 = 000000000000000000019484DD10BD27$$display$$
$$display$$C_1 = 0000000000000000019484DD10BD275D$$display$$
$$display$$C_1 = 00000000000000019484DD10BD275DB8$$display$$
$$display$$C_1 = 000000000000019484DD10BD275DB87A$$display$$
$$display$$C_1 = 0000000000019484DD10BD275DB87A48$$display$$
$$display$$C_1 = 00000000019484DD10BD275DB87A486C$$display$$
$$display$$C_1 = 000000019484DD10BD275DB87A486C72$$display$$
$$display$$C_1 = 0000019484DD10BD275DB87A486C7276$$display$$
$$display$$C_1 = 00019484DD10BD275DB87A486C7276A2$$display$$
И конечная константа:
$$display$$C_1 = 019484DD10BD275DB87A486C7276A2E6$$display$$
Остальные константы:
$$display$$C_2 = 02EBCB7920B94EBAB3F490D8E4EC87DC$$display$$
$$display$$C_3 = 037F4FA4300469E70B8ED8B4969A25B2$$display$$
$$display$$C_4 = 041555F240B19CB7A52BE3730B1BCD7B$$display$$
$$display$$C_5 = 0581D12F500CBBEA1D51AB1F796D6F15$$display$$
$$display$$C_6 = 06FE9E8B6008D20D16DF73ABEFF74AA7$$display$$
$$display$$C_7 = 076A1A5670B5F550AEA53BC79D81E8C9$$display$$
$$display$$C_8 = 082AAA2780A1FBAD895605E6163659F6$$display$$
$$display$$C_9 = 09BE2EFA901CDCF0312C4D8A6440FB98$$display$$
$$display$$C_{10} = 0AC1615EA018B5173AA2953EF2DADE2A$$display$$
$$display$$C_{11} = 0B55E583B0A5924A82D8DD5280AC7C44$$display$$
$$display$$C_{12} = 0C3FFFD5C010671A2C7DE6951D2D948D$$display$$
$$display$$C_{13} = 0DAB7B08D0AD40479407AEF96F5B36E3$$display$$
$$display$$C_{14} = 0ED434ACE0A929A09F89764DF9C11351$$display$$
$$display$$C_{15} = 0F40B071F0140EFD27F33E218BB7B13F$$display$$
$$display$$C_{16} = 1054974EC3813599D1AC0A0F2C6CB22F$$display$$
$$display$$C_{17} = 11C01393D33C12C469D642635E1A1041$$display$$
$$display$$C_{18} = 12BF5C37E3387B2362589AD7C88035F3$$display$$
$$display$$C_{19} = 132BD8EAF3855C7EDA22D2BBBAF6979D$$display$$
$$display$$C_{20} = 1441C2BC8330A92E7487E97C27777F54$$display$$
$$display$$C_{21} = 15D54661938D8E73CCFDA1105501DD3A$$display$$
$$display$$C_{22} = 16AA09C5A389E794C77379A4C39BF888$$display$$
$$display$$C_{23} = 173E8D18B334C0C97F0931C8B1ED5AE6$$display$$
$$display$$C_{24} = 187E3D694320CE3458FA0FE93A5AEBD9$$display$$
$$display$$C_{25} = 19EAB9B4539DE969E0804785482C49B7$$display$$
$$display$$C_{26} = 1A95F6106399808EEB0E9F31DEB66C05$$display$$
$$display$$C_{27} = 1B0172CD7324A7D35374D75DACC0CE6B$$display$$
$$display$$C_{28} = 1C6B689B03915283FDD1EC9A314126A2$$display$$
$$display$$C_{29} = 1DFFEC46132C75DE45ABA4F6433784CC$$display$$
$$display$$C_{30} = 1E80A3E223281C394E257C42D5ADA17E$$display$$
$$display$$C_{31} = 1F14273F33953B64F65F342EA7DB0310$$display$$
$$display$$C_{32} = 20A8ED9C45C16AF1619B141E58D8A75E$$display$$
Теперь произведем расчет раундовых ключей согласно схеме, представленной выше, возьмем ключ шифрования:
$$display$$K=7766554433221100FFEEDDCCBBAA9988$$display$$
$$display$$EFCDAB89674523011032547698BADCFE$$display$$
Тогда
$$display$$K_1=7766554433221100FFEEDDCCBBAA9988$$display$$
$$display$$K_2=EFCDAB89674523011032547698BADCFE$$display$$
$inline$K_1$inline$ будет левым подблоком сети Фейстеля, а $inline$K_2$inline$ — правым.
Выполним операцию $inline$K_1+C_1$inline$
Первый байт $inline$K_1$inline$ равен $inline$77_{16}=01110111_2$inline$
Первый байт $inline$C_1$inline$ равен $inline$01_{16}=00000001_2$inline$
$$display$$01110111_2+00000001_2=01110110_2=76_{16}$$display$$
остальные байты преобразовываются аналогично, в итоге $inline$X (K_1, C_1)=K_1+C_1$inline$:
$$display$$X (K_1, C_1)=76F2D199239F365D479495A0C9DC3BE6$$display$$
Далее выполняем нелинейное преобразование $inline$S (X (K_1, C_1))$inline$. Выполняется оно по таблице:
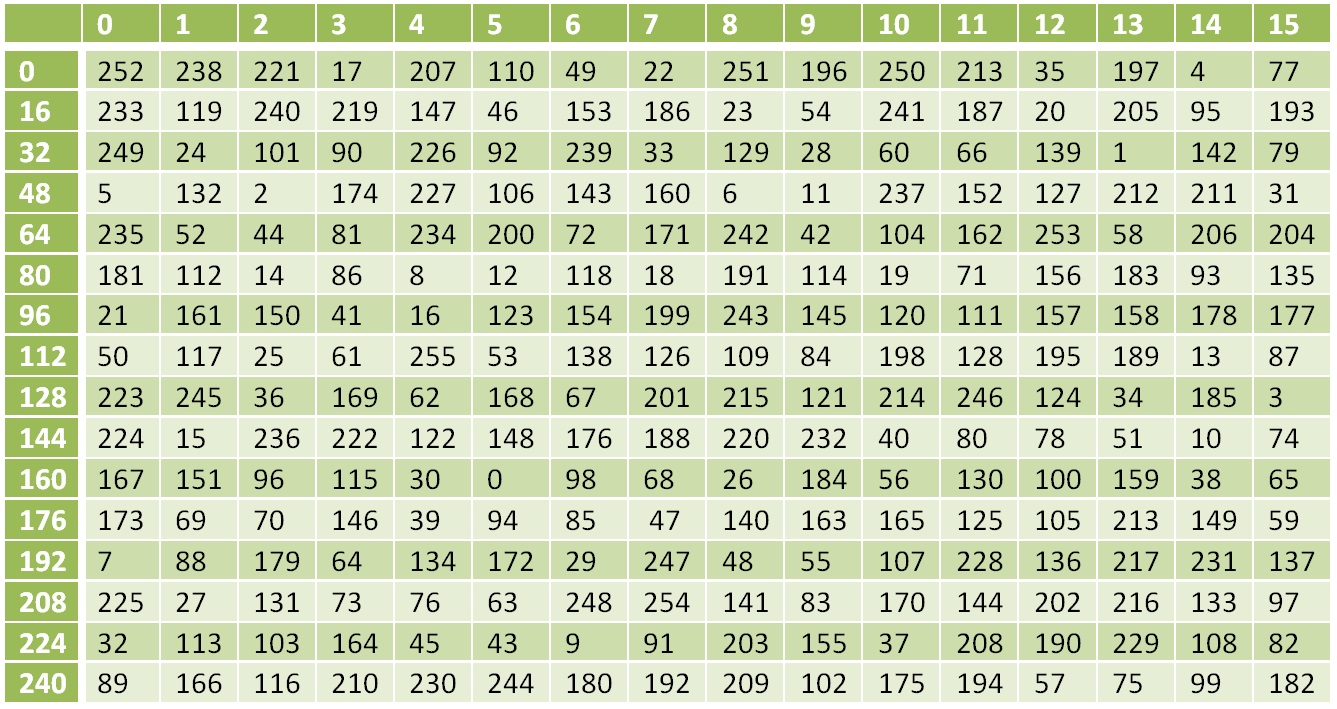
Таблица нелинейного преобразования
Число 0 заменяется на 252, 1 на 238, 17 на 119 и т.д.
$$display$$76_{16}=118_{10}$$display$$
$$display$$S (118)=138_{10}=8A_{16}$$display$$
$$display$$S (X (K_1, C_1))=8A741BE85A4A8FB7AB7A94A737CA9809$$display$$
Теперь выполним линейное преобразование $inline$L (S (X (K_1, C_1)))$inline$, оно было подробно рассмотрено при расчете итерационных констант, поэтому здесь приведем только конечный результат:
$$display$$L (S (X (K_1, C_1)))=A644615E1D0757926A5DB79D9940093D$$display$$
Согласно схеме ячейки Фейстеля выполним XOR с правым подблоком, то есть с $inline$K_2$inline$:
$$display$$X (L (S (X (K_1, C_1))), K_2)=4989CAD77A4274937A6FE3EB01FAD5C3$$display$$
И результат полученный на выходе первой ячейки Фейстеля:
$$display$$EFCDAB89674523011032547698BADCFE4989CAD77A4274937A6FE3EB01FAD5C3$$display$$
Это значение разбивается пополам и идет на вход второй ячейки Фейстеля, где используется уже вторая константа $inline$C_2$inline$. Пройдя восемь ячеек мы получим 2 следующих ключа $inline$K_3$inline$ и $inline$K_4$inline$. Выполним с ними восемь итераций сети Фейстеля, получим следующую пару ключей и так далее. Восемь итераций на пару ключей, так как первая пара у нас изначально есть, то всего выполняется 32 итерации, на каждую своя константа.
Оставшиеся ключи:
$$display$$K_3=448CC78CEF6A8D2243436915534831DB$$display$$
$$display$$K_4=04FD9F0AC4ADEB1568ECCFE9D853453D$$display$$
$$display$$K_5=ACF129F44692E5D3285E4AC468646457$$display$$
$$display$$K_6=1B58DA3428E832B532645C16359407BD$$display$$
$$display$$K_7=B198005A26275770DE45877E7540E651$$display$$
$$display$$K_8=84F98622A2912AD73EDD9F7B0125795A$$display$$
$$display$$K_9=17E5B6CD732FF3A52331C77853E244BB$$display$$
$$display$$K_{10}=43404A8EA8BA5D755BF4BC1674DDE972$$display$$
Шифрование блока
Мы рассчитали все ключи и теперь наконец-то можем перейти непосредственно к шифрованию блока текста и если вы внимательно прочли все написанное выше, то зашифровать текст уже не составит труда, так как все используемые при этом операции и их последовательность были подробно рассмотрены.
Возьмем блок открытого текста:
$$display$$T=8899AABBCCDDEEFF0077665544332211$$display$$
выполним последовательность операций X, S, L
$$display$$X (T, K_1)=FFFFFFFFFFFFFFFFFF99BB99FF99BB99$$display$$
$$display$$S (X (T, K_1))=B6B6B6B6B6B6B6B6B6E87DE8B6E87DE8$$display$$
$$display$$L (S (X (T, K_1)))=30081449922F4ACFA1B055E386B697E2$$display$$
$$display$$T_1=30081449922F4ACFA1B055E386B697E2$$display$$
$$display$$X (T_1, K_2)=DFC5BFC0F56A69CEB18201951E0C4B1C$$display$$
$$display$$S (X (T_1, K_2))=61AC3B07F47891E74524EE945F23A214$$display$$
$$display$$L (S (X (T_1, K_2)))=7290C6A158426FB396D562087A495E28$$display$$
$$display$$T_2=7290C6A158426FB396D562087A495E28$$display$$
и так далее, конечный результат будет выглядеть следующим образом:
$$display$$T_{10}=CDEDD4B9428D465A3024BCBE909D677F$$display$$
Расшифровка блока
Для расшифрования текста нужно использовать обратные операции в обратной последовательности (см. рис2).
Операция XOR обратна сама себе, обратной к операции S будет подстановка по следующей таблице:
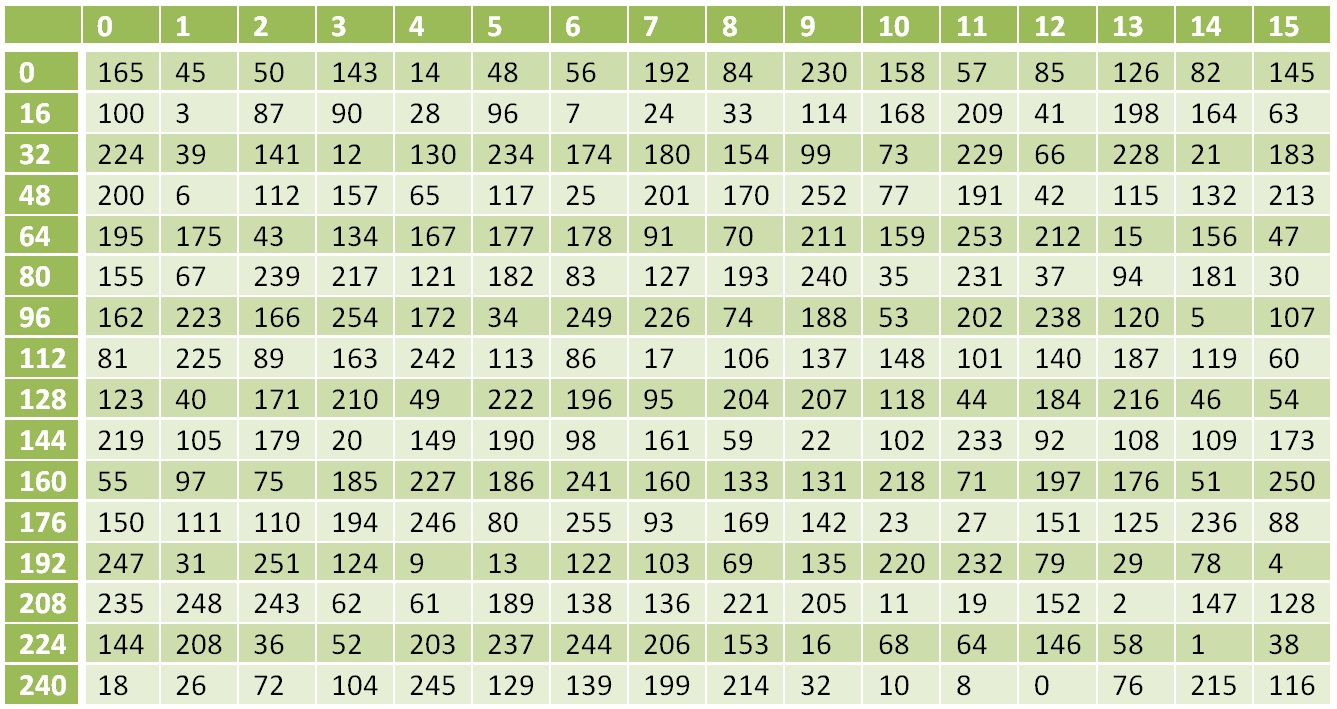
Таблица обратного нелинейного преобразования
Обратным преобразованием к функции L будет:
$$display$$a_0=a_{15}*148+a_{14}*32+a_{13}*133+a_{12}*16+$$display$$
$$display$$+a_{11}*194+a_{10}*192+a_9×1+a_8×251+a_7×1+a_6×192+a_5×194+$$display$$
$$display$$+a_4×16+a_3×133+a_2×32+a_1×148+a_0×1$$display$$
и сдвиг в сторону старшего разряда. (Повторить операции 16 раз)
Реализация в Java
Для начала определим необходимые константы
static final int BLOCK_SIZE = 16; // длина блока
// таблица прямого нелинейного преобразования
static final byte[] Pi = {
(byte) 0xFC, (byte) 0xEE, (byte) 0xDD, 0x11, (byte) 0xCF, 0x6E, 0x31, 0x16,
(byte) 0xFB, (byte) 0xC4, (byte) 0xFA, (byte) 0xDA, 0x23, (byte) 0xC5, 0x04, 0x4D,
(byte) 0xE9, 0x77, (byte) 0xF0, (byte) 0xDB, (byte) 0x93, 0x2E, (byte) 0x99, (byte) 0xBA,
0x17, 0x36, (byte) 0xF1, (byte) 0xBB, 0x14, (byte) 0xCD, 0x5F, (byte) 0xC1,
(byte) 0xF9, 0x18, 0x65, 0x5A, (byte) 0xE2, 0x5C, (byte) 0xEF, 0x21,
(byte) 0x81, 0x1C, 0x3C, 0x42, (byte) 0x8B, 0x01, (byte) 0x8E, 0x4F,
0x05, (byte) 0x84, 0x02, (byte) 0xAE, (byte) 0xE3, 0x6A, (byte) 0x8F, (byte) 0xA0,
0x06, 0x0B, (byte) 0xED, (byte) 0x98, 0x7F, (byte) 0xD4, (byte) 0xD3, 0x1F,
(byte) 0xEB, 0x34, 0x2C, 0x51, (byte) 0xEA, (byte) 0xC8, 0x48, (byte) 0xAB,
(byte) 0xF2, 0x2A, 0x68, (byte) 0xA2, (byte) 0xFD, 0x3A, (byte) 0xCE, (byte) 0xCC,
(byte) 0xB5, 0x70, 0x0E, 0x56, 0x08, 0x0C, 0x76, 0x12,
(byte) 0xBF, 0x72, 0x13, 0x47, (byte) 0x9C, (byte) 0xB7, 0x5D, (byte) 0x87,
0x15, (byte) 0xA1, (byte) 0x96, 0x29, 0x10, 0x7B, (byte) 0x9A, (byte) 0xC7,
(byte) 0xF3, (byte) 0x91, 0x78, 0x6F, (byte) 0x9D, (byte) 0x9E, (byte) 0xB2, (byte) 0xB1,
0x32, 0x75, 0x19, 0x3D, (byte) 0xFF, 0x35, (byte) 0x8A, 0x7E,
0x6D, 0x54, (byte) 0xC6, (byte) 0x80, (byte) 0xC3, (byte) 0xBD, 0x0D, 0x57,
(byte) 0xDF, (byte) 0xF5, 0x24, (byte) 0xA9, 0x3E, (byte) 0xA8, (byte) 0x43, (byte) 0xC9,
(byte) 0xD7, 0x79, (byte) 0xD6, (byte) 0xF6, 0x7C, 0x22, (byte) 0xB9, 0x03,
(byte) 0xE0, 0x0F, (byte) 0xEC, (byte) 0xDE, 0x7A, (byte) 0x94, (byte) 0xB0, (byte) 0xBC,
(byte) 0xDC, (byte) 0xE8, 0x28, 0x50, 0x4E, 0x33, 0x0A, 0x4A,
(byte) 0xA7, (byte) 0x97, 0x60, 0x73, 0x1E, 0x00, 0x62, 0x44,
0x1A, (byte) 0xB8, 0x38, (byte) 0x82, 0x64, (byte) 0x9F, 0x26, 0x41,
(byte) 0xAD, 0x45, 0x46, (byte) 0x92, 0x27, 0x5E, 0x55, 0x2F,
(byte) 0x8C, (byte) 0xA3, (byte) 0xA5, 0x7D, 0x69, (byte) 0xD5, (byte) 0x95, 0x3B,
0x07, 0x58, (byte) 0xB3, 0x40, (byte) 0x86, (byte) 0xAC, 0x1D, (byte) 0xF7,
0x30, 0x37, 0x6B, (byte) 0xE4, (byte) 0x88, (byte) 0xD9, (byte) 0xE7, (byte) 0x89,
(byte) 0xE1, 0x1B, (byte) 0x83, 0x49, 0x4C, 0x3F, (byte) 0xF8, (byte) 0xFE,
(byte) 0x8D, 0x53, (byte) 0xAA, (byte) 0x90, (byte) 0xCA, (byte) 0xD8, (byte) 0x85, 0x61,
0x20, 0x71, 0x67, (byte) 0xA4, 0x2D, 0x2B, 0x09, 0x5B,
(byte) 0xCB, (byte) 0x9B, 0x25, (byte) 0xD0, (byte) 0xBE, (byte) 0xE5, 0x6C, 0x52,
0x59, (byte) 0xA6, 0x74, (byte) 0xD2, (byte) 0xE6, (byte) 0xF4, (byte) 0xB4, (byte) 0xC0,
(byte) 0xD1, 0x66, (byte) 0xAF, (byte) 0xC2, 0x39, 0x4B, 0x63, (byte) 0xB6
};
// таблица обратного нелинейного преобразования
static final byte[] reverse_Pi = {
(byte) 0xA5, 0x2D, 0x32, (byte) 0x8F, 0x0E, 0x30, 0x38, (byte) 0xC0,
0x54, (byte) 0xE6, (byte) 0x9E, 0x39, 0x55, 0x7E, 0x52, (byte) 0x91,
0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18,
0x21, 0x72, (byte) 0xA8, (byte) 0xD1, 0x29, (byte) 0xC6, (byte) 0xA4, 0x3F,
(byte) 0xE0, 0x27, (byte) 0x8D, 0x0C, (byte) 0x82, (byte) 0xEA, (byte) 0xAE, (byte) 0xB4,
(byte) 0x9A, 0x63, 0x49, (byte) 0xE5, 0x42, (byte) 0xE4, 0x15, (byte) 0xB7,
(byte) 0xC8, 0x06, 0x70, (byte) 0x9D, 0x41, 0x75, 0x19, (byte) 0xC9,
(byte) 0xAA, (byte) 0xFC, 0x4D, (byte) 0xBF, 0x2A, 0x73, (byte) 0x84, (byte) 0xD5,
(byte) 0xC3, (byte) 0xAF, 0x2B, (byte) 0x86, (byte) 0xA7, (byte) 0xB1, (byte) 0xB2, 0x5B,
0x46, (byte) 0xD3, (byte) 0x9F, (byte) 0xFD, (byte) 0xD4, 0x0F, (byte) 0x9C, 0x2F,
(byte) 0x9B, 0x43, (byte) 0xEF, (byte) 0xD9, 0x79, (byte) 0xB6, 0x53, 0x7F,
(byte) 0xC1, (byte) 0xF0, 0x23, (byte) 0xE7, 0x25, 0x5E, (byte) 0xB5, 0x1E,
(byte) 0xA2, (byte) 0xDF, (byte) 0xA6, (byte) 0xFE, (byte) 0xAC, 0x22, (byte) 0xF9, (byte) 0xE2,
0x4A, (byte) 0xBC, 0x35, (byte) 0xCA, (byte) 0xEE, 0x78, 0x05, 0x6B,
0x51, (byte) 0xE1, 0x59, (byte) 0xA3, (byte) 0xF2, 0x71, 0x56, 0x11,
0x6A, (byte) 0x89, (byte) 0x94, 0x65, (byte) 0x8C, (byte) 0xBB, 0x77, 0x3C,
0x7B, 0x28, (byte) 0xAB, (byte) 0xD2, 0x31, (byte) 0xDE, (byte) 0xC4, 0x5F,
(byte) 0xCC, (byte) 0xCF, 0x76, 0x2C, (byte) 0xB8, (byte) 0xD8, 0x2E, 0x36,
(byte) 0xDB, 0x69, (byte) 0xB3, 0x14, (byte) 0x95, (byte) 0xBE, 0x62, (byte) 0xA1,
0x3B, 0x16, 0x66, (byte) 0xE9, 0x5C, 0x6C, 0x6D, (byte) 0xAD,
0x37, 0x61, 0x4B, (byte) 0xB9, (byte) 0xE3, (byte) 0xBA, (byte) 0xF1, (byte) 0xA0,
(byte) 0x85, (byte) 0x83, (byte) 0xDA, 0x47, (byte) 0xC5, (byte) 0xB0, 0x33, (byte) 0xFA,
(byte) 0x96, 0x6F, 0x6E, (byte) 0xC2, (byte) 0xF6, 0x50, (byte) 0xFF, 0x5D,
(byte) 0xA9, (byte) 0x8E, 0x17, 0x1B, (byte) 0x97, 0x7D, (byte) 0xEC, 0x58,
(byte) 0xF7, 0x1F, (byte) 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67,
0x45, (byte) 0x87, (byte) 0xDC, (byte) 0xE8, 0x4F, 0x1D, 0x4E, 0x04,
(byte) 0xEB, (byte) 0xF8, (byte) 0xF3, 0x3E, 0x3D, (byte) 0xBD, (byte) 0x8A, (byte) 0x88,
(byte) 0xDD, (byte) 0xCD, 0x0B, 0x13, (byte) 0x98, 0x02, (byte) 0x93, (byte) 0x80,
(byte) 0x90, (byte) 0xD0, 0x24, 0x34, (byte) 0xCB, (byte) 0xED, (byte) 0xF4, (byte) 0xCE,
(byte) 0x99, 0x10, 0x44, 0x40, (byte) 0x92, 0x3A, 0x01, 0x26,
0x12, 0x1A, 0x48, 0x68, (byte) 0xF5, (byte) 0x81, (byte) 0x8B, (byte) 0xC7,
(byte) 0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, (byte) 0xD7, 0x74
};
// вектор линейного преобразования
static final byte[] l_vec = {
1, (byte) 148, 32, (byte) 133, 16, (byte) 194, (byte) 192, 1,
(byte) 251, 1, (byte) 192, (byte) 194, 16, (byte) 133, 32, (byte) 148
};
// массив для хранения констант
static byte[][] iter_C = new byte[32][16];
// массив для хранения ключей
static byte[][] iter_key = new byte[10][64];
Создадим все основные функции:
// функция X
static private byte[] GOST_Kuz_X(byte[] a, byte[] b)
{
int i;
byte[] c = new byte[BLOCK_SIZE];
for (i = 0; i < BLOCK_SIZE; i++)
c[i] = (byte) (a[i] ^ b[i]);
return c;
}
// Функция S
static private byte[] GOST_Kuz_S(byte[] in_data)
{
int i;
byte[] out_data = new byte[in_data.length];
for (i = 0; i < BLOCK_SIZE; i++)
{
int data = in_data[i];
if(data < 0)
{
data = data + 256;
}
out_data[i] = Pi[data];
}
return out_data;
}
Для реализации функции L нам понадобится несколько вспомогательных функций, одна для расчета умножения чисел в поле Галуа, и одна для сдвига.
// умножение в поле Галуа
static private byte GOST_Kuz_GF_mul(byte a, byte b)
{
byte c = 0;
byte hi_bit;
int i;
for (i = 0; i < 8; i++)
{
if ((b & 1) == 1)
c ^= a;
hi_bit = (byte) (a & 0x80);
a <<= 1;
if (hi_bit < 0)
a ^= 0xc3; //полином x^8+x^7+x^6+x+1
b >>= 1;
}
return c;
}
// функция R сдвигает данные и реализует уравнение, представленное для расчета L-функции
static private byte[] GOST_Kuz_R(byte[] state)
{
int i;
byte a_15 = 0;
byte[] internal = new byte[16];
for (i = 15; i >= 0; i--)
{
if(i == 0)
internal[15] = state[i];
else
internal[i - 1] = state[i];
a_15 ^= GOST_Kuz_GF_mul(state[i], l_vec[i]);
}
internal[15] = a_15;
return internal;
}
static private byte[] GOST_Kuz_L(byte[] in_data)
{
int i;
byte[] out_data = new byte[in_data.length];
byte[] internal = in_data;
for (i = 0; i < 16; i++)
{
internal = GOST_Kuz_R(internal);
}
out_data = internal;
return out_data;
}
Обратные функции:
// функция S^(-1)
static private byte[] GOST_Kuz_reverse_S(byte[] in_data)
{
int i;
byte[] out_data = new byte[in_data.length];
for (i = 0; i < BLOCK_SIZE; i++)
{
int data = in_data[i];
if(data < 0)
{
data = data + 256;
}
out_data[i] = reverse_Pi[data];
}
return out_data;
}
static private byte[] GOST_Kuz_reverse_R(byte[] state)
{
int i;
byte a_0;
a_0 = state[15];
byte[] internal = new byte[16];
for (i = 1; i < 16; i++)
{
internal[i] = state[i - 1];
a_0 ^= GOST_Kuz_GF_mul(internal[i], l_vec[i]);
}
internal[0] = a_0;
return internal;
}
static private byte[] GOST_Kuz_reverse_L(byte[] in_data)
{
int i;
byte[] out_data = new byte[in_data.length];
byte[] internal;
internal = in_data;
for (i = 0; i < 16; i++)
internal = GOST_Kuz_reverse_R(internal);
out_data = internal;
return out_data;
}
// функция расчета констант
static private void GOST_Kuz_Get_C()
{
int i;
byte[][] iter_num = new byte[32][16];
for (i = 0; i < 32; i++)
{
for(int j = 0; j < BLOCK_SIZE; j++)
iter_num[i][j] = 0;
iter_num[i][0] = (byte) (i+1);
}
for (i = 0; i < 32; i++)
{
iter_C[i] = GOST_Kuz_L(iter_num[i]);
}
}
// функция, выполняющая преобразования ячейки Фейстеля
static private byte[][] GOST_Kuz_F(byte[] in_key_1, byte[] in_key_2, byte[] iter_const)
{
byte[] internal;
byte[] out_key_2 = in_key_1;
internal = GOST_Kuz_X(in_key_1, iter_const);
internal = GOST_Kuz_S(internal);
internal = GOST_Kuz_L(internal);
byte[] out_key_1 = GOST_Kuz_X(internal, in_key_2);
byte key[][] = new byte[2][];
key[0] = out_key_1;
key[1] = out_key_2;
return key;
}
// функция расчета раундовых ключей
public void GOST_Kuz_Expand_Key(byte[] key_1, byte[] key_2)
{
int i;
byte[][] iter12 = new byte[2][];
byte[][] iter34 = new byte[2][];
GOST_Kuz_Get_C();
iter_key[0] = key_1;
iter_key[1] = key_2;
iter12[0] = key_1;
iter12[1] = key_2;
for (i = 0; i < 4; i++)
{
iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[0 + 8 * i]);
iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[1 + 8 * i]);
iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[2 + 8 * i]);
iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[3 + 8 * i]);
iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[4 + 8 * i]);
iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[5 + 8 * i]);
iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[6 + 8 * i]);
iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[7 + 8 * i]);
iter_key[2 * i + 2] = iter12[0];
iter_key[2 * i + 3] = iter12[1];
}
}
// функция шифрования блока
public byte[] GOST_Kuz_Encript(byte[] blk)
{
int i;
byte[] out_blk = new byte[BLOCK_SIZE];
out_blk = blk;
for(i = 0; i < 9; i++)
{
out_blk = GOST_Kuz_X(iter_key[i], out_blk);
out_blk = GOST_Kuz_S(out_blk);
out_blk = GOST_Kuz_L(out_blk);
}
out_blk = GOST_Kuz_X(out_blk, iter_key[9]);
return out_blk;
}
//функция расшифрования блока
public byte[] GOST_Kuz_Decript(byte[] blk)
{
int i;
byte[] out_blk = new byte[BLOCK_SIZE];
out_blk = blk;
out_blk = GOST_Kuz_X(out_blk, iter_key[9]);
for(i = 8; i >= 0; i--)
{
out_blk = GOST_Kuz_reverse_L(out_blk);
out_blk = GOST_Kuz_reverse_S(out_blk);
out_blk = GOST_Kuz_X(iter_key[i], out_blk);
}
return out_blk;
}
Ну, и функция main
static byte[] key_1 =
{0x77, 0x66, 0x55, 0x44, 0x33, 0x22, 0x11, 0x00, (byte) 0xff, (byte) 0xee,
(byte) 0xdd, (byte) 0xcc, (byte) 0xbb, (byte) 0xaa, (byte) 0x99, (byte) 0x88};
static byte[] key_2 =
{(byte) 0xef, (byte) 0xcd, (byte) 0xab, (byte) 0x89, 0x67, 0x45, 0x23, 0x01,
0x10, 0x32, 0x54, 0x76, (byte) 0x98, (byte) 0xba, (byte) 0xdc, (byte) 0xfe};
static byte[] blk = DatatypeConverter.parseHexBinary("8899aabbccddeeff0077665544332211");
public static void main(String[] args)
{
GOST_Kuz_Expand_Key(key_1, key_2);
byte[] encriptBlok = GOST_Kuz_Encript(blk);
System.out.println(DatatypeConverter.printHexBinary(encriptBlok));
byte[] decriptBlok = GOST_Kuz_Decript(encriptBlok);
System.out.println(DatatypeConverter.printHexBinary(decriptBlok));
}
Мы научились шифровать блок данных, чтобы зашифровать текст, длина которого больше длины блока, существует несколько режимов, описанных в стандарте — ГОСТ 34.13–2015:
- режим простой замены (Electronic Codebook, ECB);
- режим гаммирования (Counter, CTR);
- режим гаммирования с обратной связью по выходу (Output Feedback, OFB);
- режим простой замены с зацеплением (Cipher Block Chaining, CBC);
- режим гаммирования с обратной связью по шифротексту (Cipher Feedback, CFB);
- режим выработки имитовставки (Message Authentication Code, MAC).
Во всех режимах длина текста всегда должна быть кратна длине блока, поэтому текст всегда дополняется справа одним единичным битом и нулями до длины блока.
Самый простой режим — это режим простой замены. В этом режиме текст разбивается на блоки, затем каждый блок зашифровывается отдельно от остальных, затем блоки зашифрованного текста склеиваются вместе и мы получаем шифрованное сообщение. Данный режим является как самым простым, так и самым уязвимым и почти не применяется на практике.
Остальные режимы возможно будут рассмотрены подробно чуть позже.
