[Из песочницы] Коронавирус: мы все умрём?
Что мы говорим Богу смерти? — Не сегодня.
Сирио Форель, сериал «Игра престолов».
Насколько действительно опасен коронавирус COVID-19? Сколько людей умрёт от коронавируса в мире? А сколько — в России? Так ли необходимы жесткие меры, принимаемые для борьбы с коронавирусом в большинстве стран мира? Что принесет больше ущерба: смерть людей от коронавируса или падение экономики, вызванное ограничительными мерами?
Чтобы ответить на эти актуальные вопросы, необходимо провести математическое моделирование и спрогнозировать ущерб от коронавируса для отдельных стран и для мира в целом. Построению таких прогнозов посвящена данная статья.
Чтобы сделать материал доступным для всех читателей, в начале статьи мы сконцентрируемся на качественном анализе, и красивых картинках. А в самом конце для интересующихся приведем исходный код для расчетов, выполненных на языке Python.
Считаем только смерти
Заметим, что ущерб от COVID-19 мы будем оценивать в количестве человеческих смертей, связанных с этим заболеванием. Прогнозированию количества умерших от коронавируса будет посвящена большая часть статьи. Мы вообще отказались от рассмотрения количества заболевших коронавирусом и прогнозирования их числа. Тому есть несколько причин. Главная состоит в том, что невозможно сопоставить статистику по количеству заболевших COVID-19 в разных странах. В одних странах методы экспресс-тестирования доступны гораздо больше, чем в других. В одних странах проводится практически поголовная проверка населения, а в других проверяют только людей с выраженными симптомами. Учитывая, что в значительном количестве случаев заболевание проходит практически бессимптомно, мы видим огромный разброс в количестве умерших среди заболевших: от менее чем 0,5% до более чем 3,5%.
Скорее всего, в значительной степени разброс в данных по смертности обусловлен в качестве выявления заболевших COVID-19.
Статистика смертности в данном случае выглядит гораздо более надежно. Естественно, мы можем сталкиваться как с занижением количества смертей, когда причиной смерти указывается не коронавирус, а сопутствующее заболевание, так и наоборот, завышения, когда COVID-19 диагностируется ошибочно, а человек умирает, например, от сезонного гриппа. Однако можно ожидать, что статистика по смертям более достоверна, т.к. бессимптомное заболевание с высокой степенью вероятности может вообще пройти мимо внимания специалистов, а каждый случай смерти медики вынуждены анализировать.
Также заметим, что реальный ущерб обществу причиняет смерть его членов, а не легкое заболевание, которое относительно быстро проходит.
Вы думали, миром правит экспонента? А вот и нет!
Как только мы начинаем прогнозировать количество смертей, сразу сталкиваемся с первым мифом: от коронавируса умрут десятки, а то и сотни миллионов человек. Этот миф основан на убеждении, что миром правит экспонента. Взгляните на график.
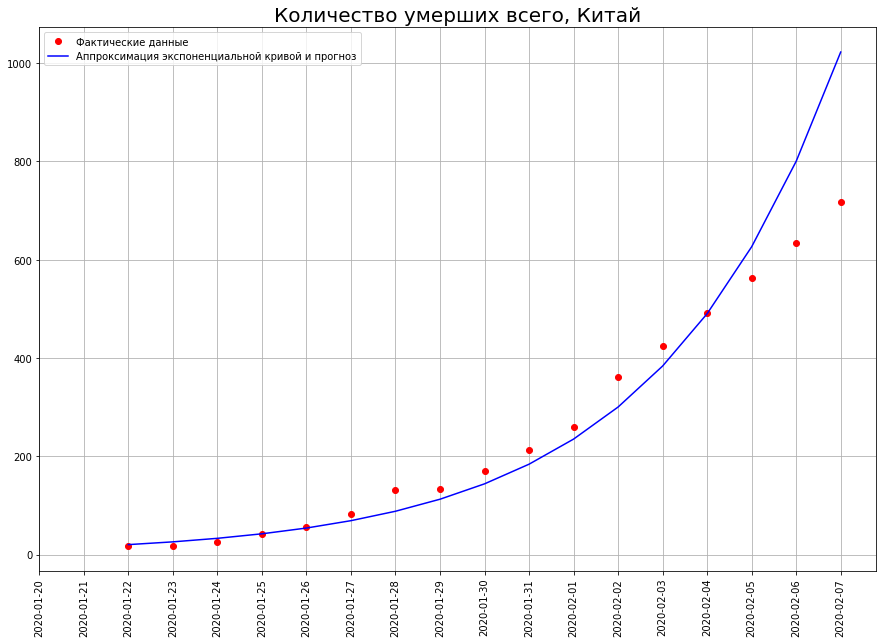
На нём изображено количество умерших от COVID-19 в Китае по состоянию на 7 февраля. Если мы построим на основе этого графика прогноз, используя экспоненциальную функцию, то получим, что уже к 29 февраля в Китае должно было бы умереть 50 миллионов человек!

А сколько умерло в действительности? 2837 человек. Откуда такая колоссальная разница?
Все дело в том, что миром правит не экспонента, а логистическая кривая.
В отличие от экспоненты, логистическую кривую не проходят не только в школе, но даже в ведущих технических университетах (например, на Физфаке МГУ и на Физтехе). Поэтому физики и вообще технари нередко не имеют о ней представления.
Тем не менее, огромное количество явлений в экономике, биологии, социологии, науке и технике развивается в полном соответствии с этой математической моделью. Давайте приглядимся к ней повнимательнее. Вот она. По оси х отложено время, по у — число, которое характеризует исследуемое нами явления (в нашем случае, количество смертей от коронавируса).
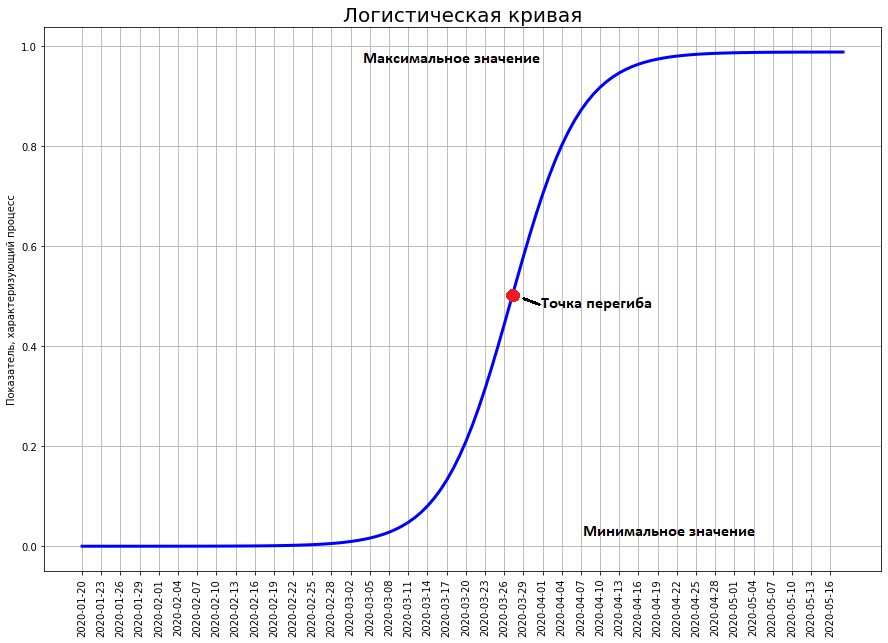
Коварная кривая, которая обламывает весь хайп
Логистическая кривая показывает переход между двумя устойчивыми состояниями. Нижнее состояние традиционно считается равным нулю. Верхнее состояние — это максимум, который в принципе может достичь исследуемое явление. Кривая приближается к нему как угодно близко, но никогда не достигает максимального значения.
Самая важная точка на кривой — это точка перегиба. Она расположена ровно посередине между минимум и максимумом. Именно в этой точке максимально скорость роста кривой. Но в ней происходит перегиб. До этой точки рост кривой только ускоряется. После — только затухает.
Обычно некоторое явление поначалу никто не замечает (как не замечали коронавирус до конца января). В этот момент значение кривой близко к нулю. Постепенно явление нарастает, его начинают замечать, вокруг него возникает хайп. Хайп может быть как положительным (как, например, в момент полета Гагарина люди на всей Земле заболели космосом), так и отрицательным (ситуация с нынешним коронавирусом). В момент хайпа все предсказывают, что явление приобретет невероятные масштабы и перевернет мир. Так, в момент полета Гагарина, даже профессионалы думали, что покорение Солнечной системы произойдет еще в ХХ веке. И совершенно не ожидали, что все успехи космонавтики закончатся в 1969 году с высадкой человека на Луну.
Именно в момент максимального хайпа кривая достигает половины от своего будущего максимума. Затем рост затухает и явление совершенно не оправдывает возлагавшихся на него надежд (равно как и опасений).
Китайская логистическая кривая
Давайте посмотрим, что произошло в Китае.
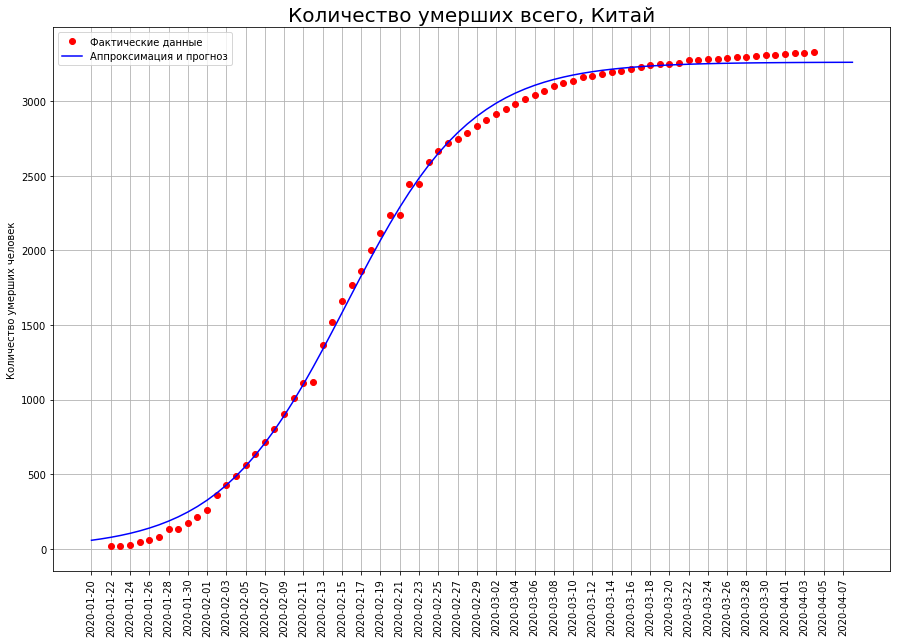
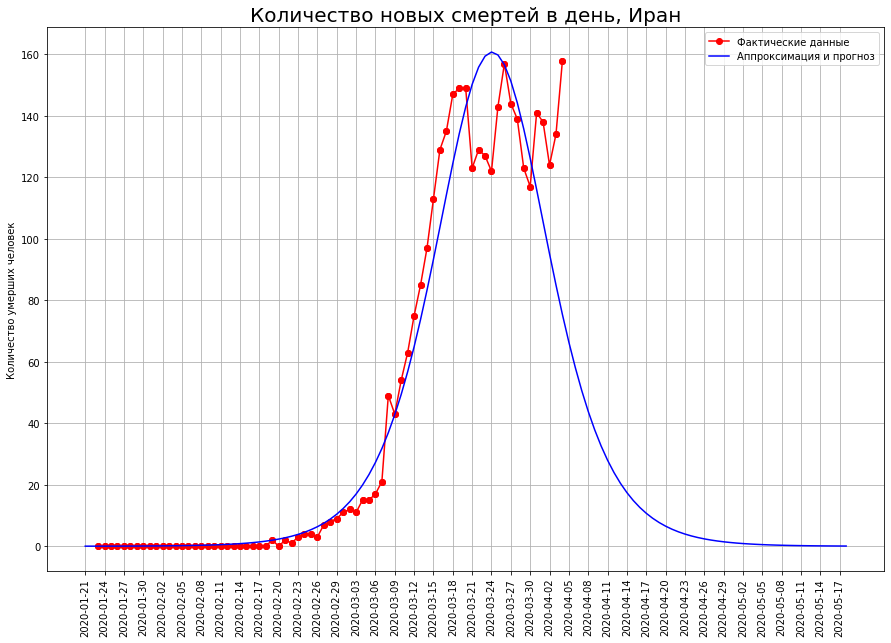
На графике ниже красными точками отмечено количество смертей от вируса на заданную дату. Синяя кривая — это логистическая кривая, аппроксимирующая реальные данные. Мы видим, что данные ложатся на нее практически идеально. На графике ниже показано количество смертей, произошедших в определённую дату. Фактически, это разница между значениями логистической кривой на сегодня и на вчера. С математической точки зрения, это первая производная от логистической кривой.
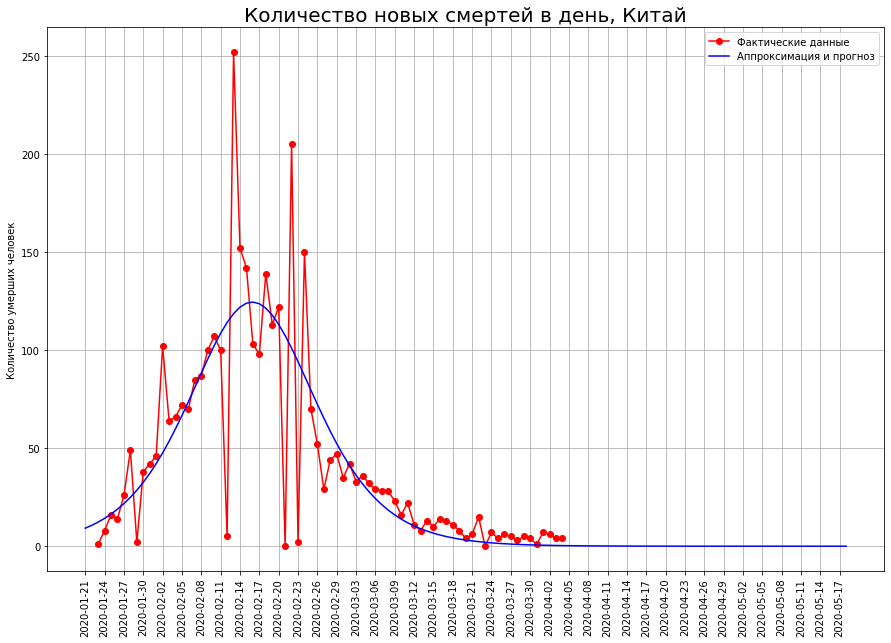
Мы видим, что сначала количество новых смертей растет практически по экспоненте. Затем рост начинает замедляться, кривая новых смертей достигает максимума в точке перегиба, когда логистическая кривая достигает половины от своего максимального значения. Затем количество новых смертей снижается, и устремляется к нулю. Красными точками отмечены новые смерти, синяя кривая — аппроксимирующая их производная от логистической кривой.
Заметим, что логистическая кривая симметрична относительно точки ее перегиба, а ее первая производная — относительно вертикальной линии, проходящей через эту точку. Также отметим, что реальные данные идеально лежат на логистической кривой, но «пляшут» относительно ее первой производной. Дело в том, что показатель смерти в точке подвержен высокому разбросу, а показатель общего количества смертей — это сумма таких показателей. Она сглаживается в соответствии с центральной предельной теоремой.
Итак, мы видим, что логистическую кривую можно эффективно использовать для прогнозирования смертей от коронавируса. Тут важным свойством является ее симметричность. Когда точка перегиба достигнута, по одной половинке кривой мы можем с высокой точностью восстановить другую половинку.
В свою очередь, для того, чтобы определить, достигнута ли точка перегиба, надо просто посмотреть на график первой производной. Как только он пошел вниз — соответствующая точка достигнута.
Чем закончится итальянская катастрофа?
Обратим наш взгляд на три страны на букву «И»: Италию, Иран и Испанию. Глядя на кривые смертей в конкретную дату, мы видим, что, скорее всего, пик катастрофы там пройден, и настало время подводить итоги.


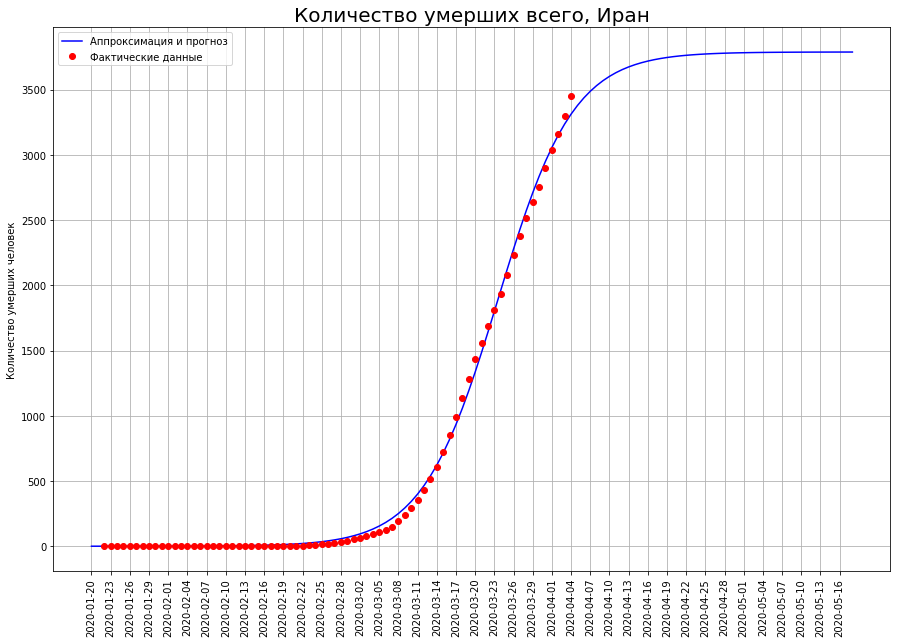
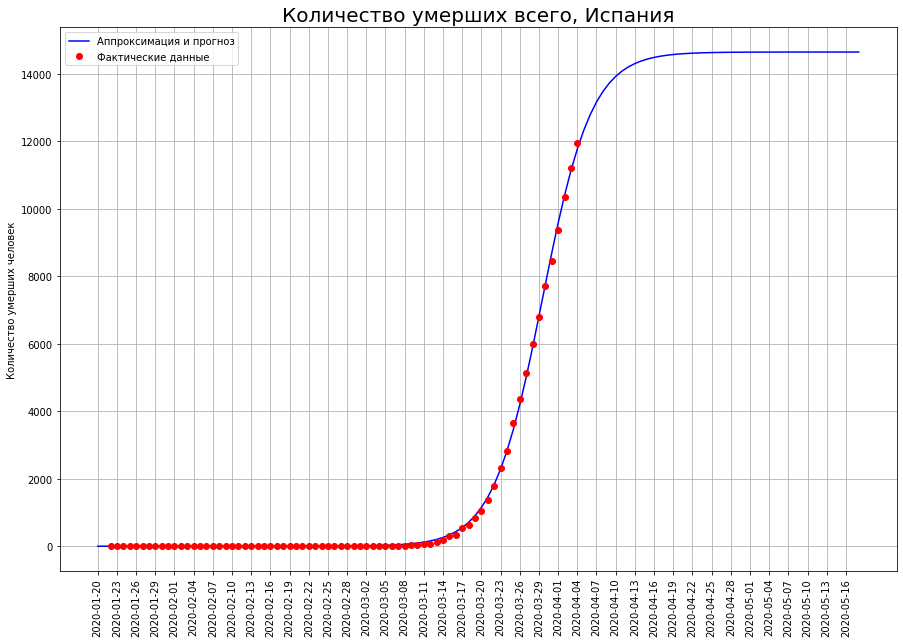

По нашим прогнозам, всего от COVID-19 умрут:
в Италии — около 19 тысяч человек,
в Иране — около 4 тысяч человек,
в Испании — около 15 тысяч человек.
На полпути к финальной смертности
Эпидемия в Германии, кажется, достигла своего пика и общее количество умерших от коронавируса в этой стране составит около 2,6 тысяч человек.


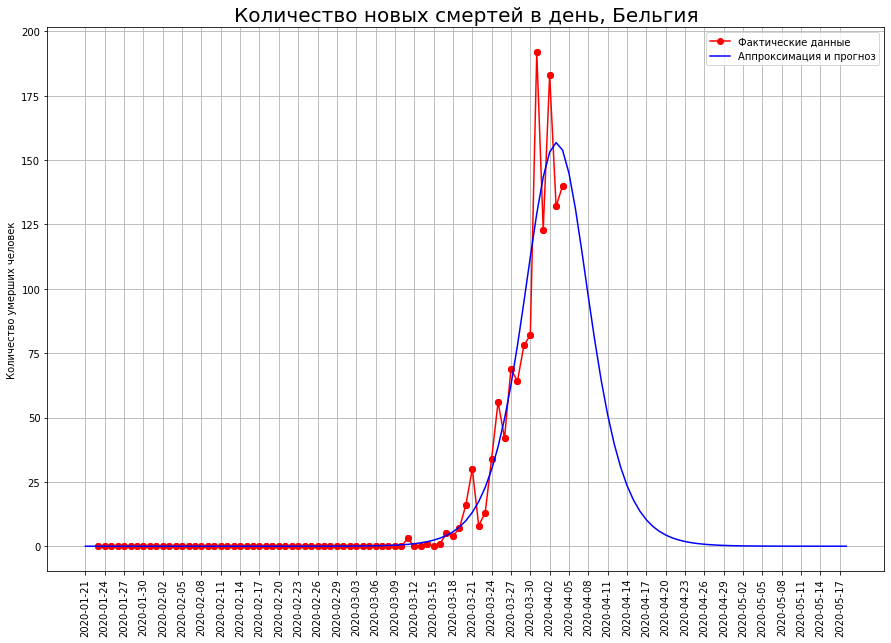
В таких странах, как Нидерланды, Швейцария и Бельгия, математическое моделирование показывает, что эпидемия находится в точке перегиба. Если этот так, то ожидаемое количество умерших в них:
в Нидерландах — около 2,5 тысяч человек,
в Швейцарии — около 1,1 тысячи человек,
в Бельгии — около 2,2 тысяч человек.




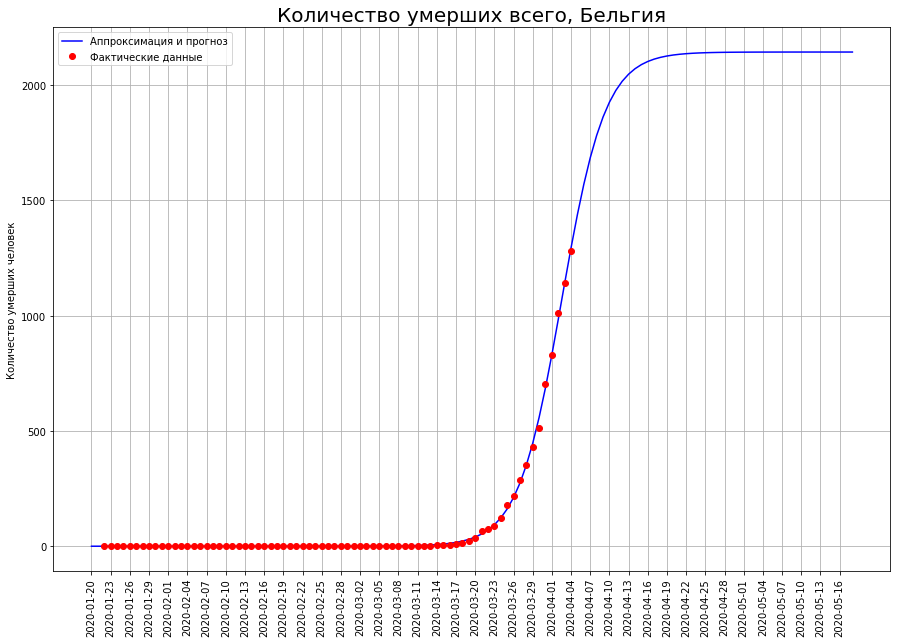
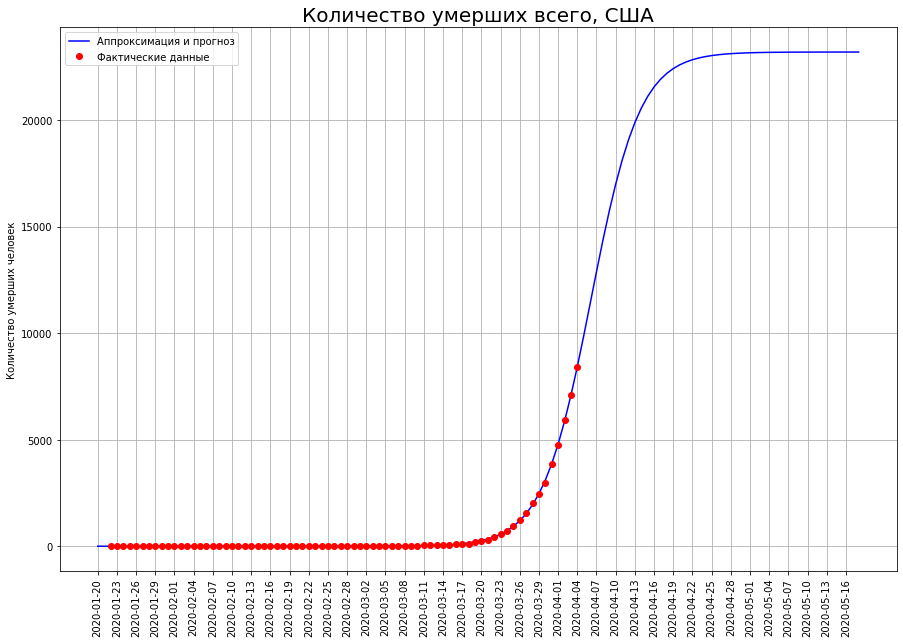
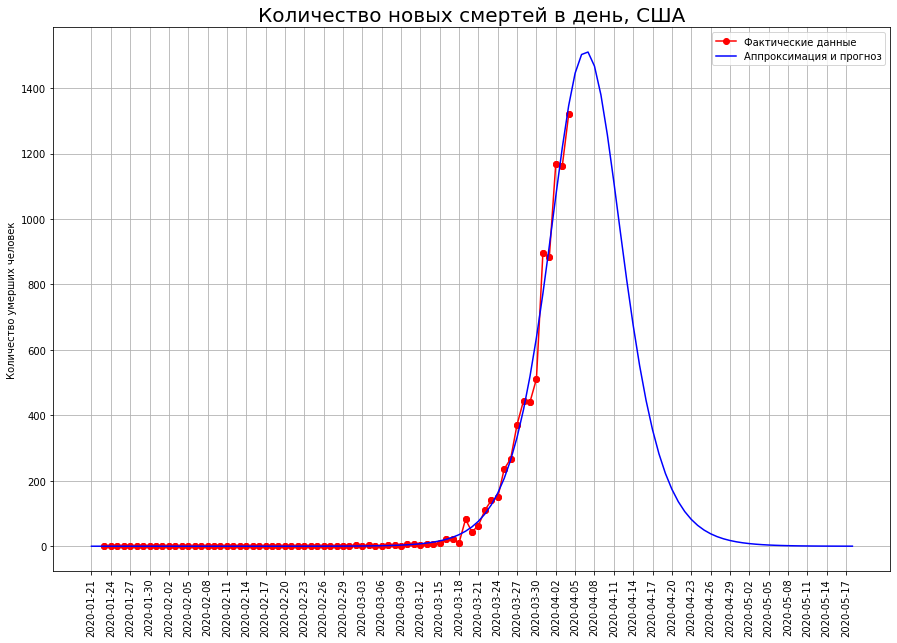
Для кого-то все только начинается
В США точка перегиба еще не пройдена, поэтому прогноз по ним может значительно скорректироваться. В настоящее время он составляет 23 тысячи человек.
Великобритания — новый эпицентр трагедии?
Наконец, для двух стран сохраняется высокая неопределенность в достижении точки перегиба. Это Великобритания и Франция.


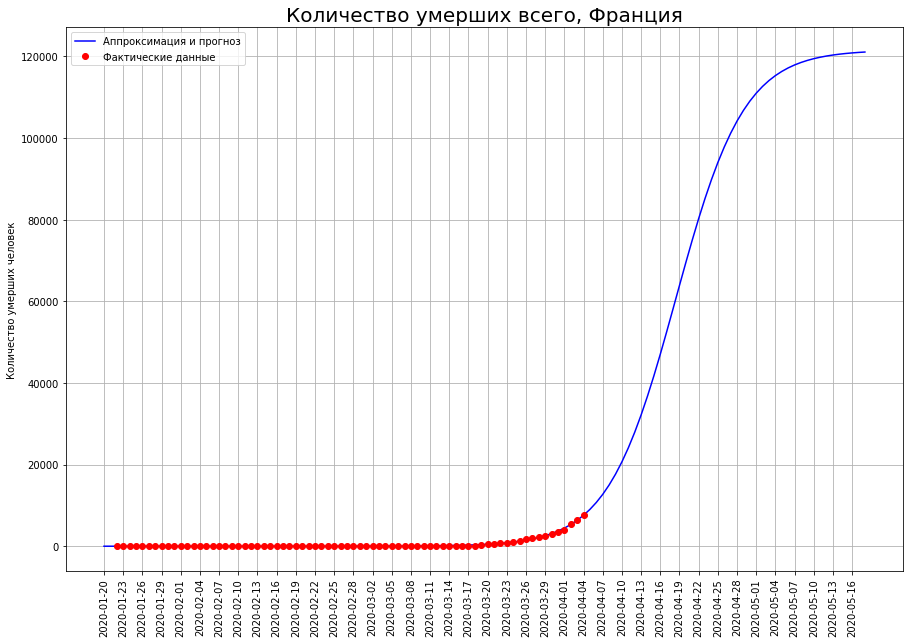
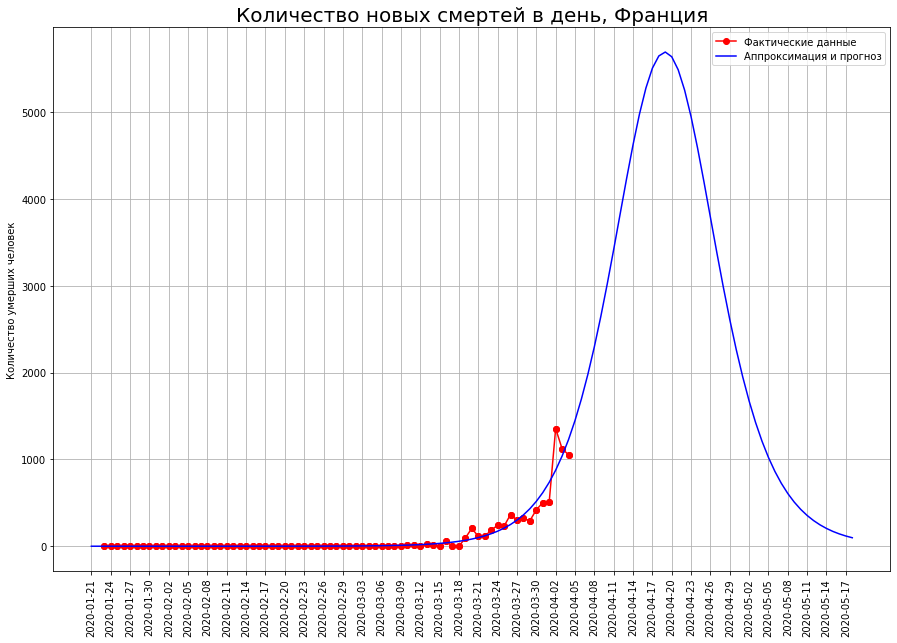
Прогнозы конечного числа смертей по ним постоянно повышаются. В настоящее время они составляют:
- по Великобритании — около 33 тысяч человек,
- по Франции — около 12 тысяч человек.
Автор надеется, что данные прогнозы являются результатом случайных флуктуаций, и в ближайшие дни они скорректируются в меньшую сторону.
Особое беспокойство у автора вызывает Великобритания. По данным на 25.03 автор прогнозировал в этой стране смертность на уровне 1 тысячи человек, по данным на 01.04 — на уровне 8 тысяч, теперь прогноз показывает уже 33 тысячи. Ни по одной другой стране прогнозы не имеют такой волатильности.
Возможно, в Великобританию постепенно перемещается эпицентр трагедии смертей от коронавируса. Также возможно, что развитие ситуации в стране связано с изначально безответственной политикой Бориса Джонсона, который до последнего отказывался вводить жесткие ограничения и надеялся на «иммунизацию стада». В этом случае, автор надеется, что граждане, о которых Джонсон выразился столь непочтительным образом, вспомнят ему эту политику на очередных, а скорее — внеочередных выборах.
Прогноз по России
Поскольку в России эпидемия только начинается, прогнозировать количество умерших с помощью логистической кривой не получится. Ниже мы применим другой метод прогноза.
А что в мировом масштабе?
Пришло время простроить прогноз для всего мира.

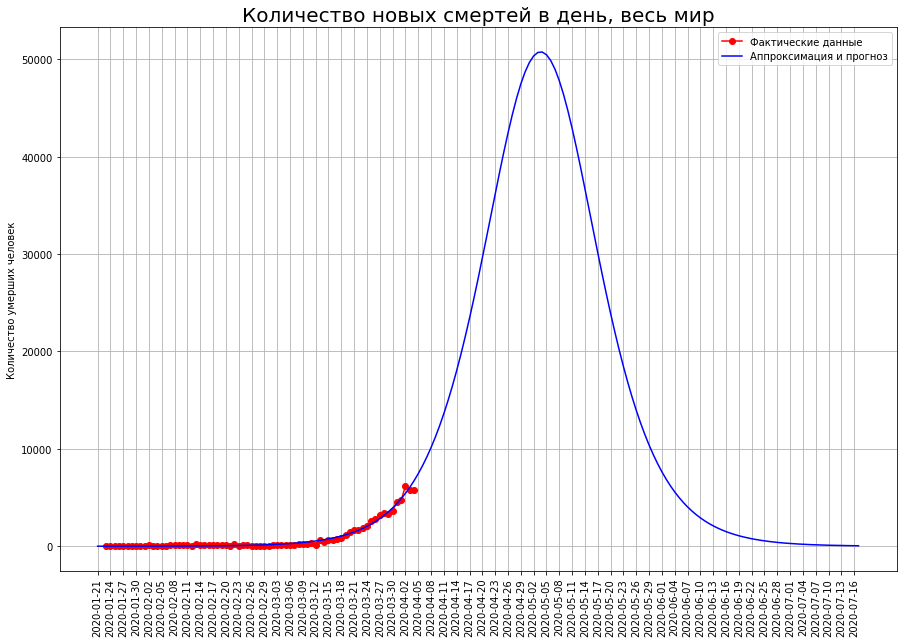
Построенная нами логистическая кривая дает такие результаты: пик кризиса придется на первую декаду мая, закончится эпидемия в середине июля. Она унесет жизни примерно 1 миллиона 800 тысяч человек.
Поскольку эпидемия в мировом масштабе только разгорается, прогноз на основе логистической кривой может дать неверный результат, поэтому воспользуемся альтернативным методом прогнозирования.
Рассмотрим страны, для которых мы сделали прогнозы.
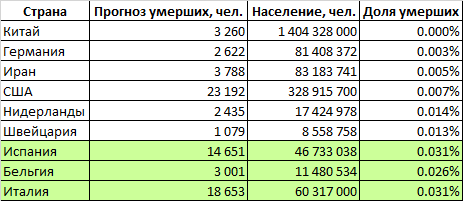
В таблице определена доля населения, этих стран, которая умрет от коронавируса (Великобритания и Франция временно исключены ввиду высокой неопределенности прогнозов). Мы видим, что значительно отличаются две группы стран. В таких странах как Италия, Испания и Бельгия, смертность прогнозируется на уровне 0,029% от населения. В более благополучной группе стран (Китай, Германия, Иран, США, Нидерланды, Швейцария) уровень смертности ожидается в районе 0,007% — в 4 раза ниже.
Можно предположить, что для мира в целом будет характерен более высокий уровень смертности. Дело в том, что в нашем анализе мы рассмотрели относительно богатые страны с дееспособными правительствами, имеющие как финансовые, так и организационные ресурсы для борьбы с эпидемией. Но на Земле много государств, которые обладают гораздо более скромными возможностями, как с финансовой точки зрения, так и с организационной. Многие из этих стран весьма густо населены. Можно предположить, что в этих странах эпидемия соберет даже больший процент жертв, чем в богатых Италии, Испании и Бельгии. С другой стороны, и доля пожилого населения в таких странах меньше, что снижает потенциальную смертность.
Если оценить мировую смертность на уровне худшей группы стран, то в мире умрет около 2 миллиона 100 тысяч человек. Если использовать средние значения — то около 900 тысяч.
Наш пессимистический прогноз для числа умерших в мире, рассчитанный на основе доли умершего населения, оказался удивительно близок с прогнозом, рассчитанным на основе логистической кривой.
Таким образом, в мире умрет 1–2 миллиона человек, причем цифра 2 миллиона более вероятна.
Что же будет с Родиной и с нами?
Что касается России, то при численности населения 148 миллионов человек оптимистический прогноз (на основании среднего по всем странам, кроме тройки аутсайдеров) составляет 10 тысяч человек. А пессимистический (основанный на смертности на уровне Италии, Испании и Бельгии) — 40 тысяч.
При этом цифра 10 тысяч гораздо более вероятна. Дело в том, что у России есть несколько благоприятных факторов: низкая плотность населения, большие расстояния между крупными городами, относительно низкие миграционные потоки между регионами (исключая столичный регион), решительность, адекватность и своевременность действий властей по борьбе с эпидемией. Эти факторы дают надежду избежать развития ситуации по итальяно-испанско-бельгийскому варианту.
Что касается сроков завершения эпидемии в России, обратимся на график ниже. На нем мы изобразили логистические кривые для разных стран на одном графике. При этом мы отнормировали все кривые по высоте так, чтобы максимальным значением была единица, и совместили точку перегиба, расположив ее в нуле.
Из графика видно, что эпидемия завершается за 40–60 дней. Если взять в качестве точки отсчета 30 марта, то в России эпидемия должна будет завершиться к 10–30 мая.
Оправданны ли жертвы?
И, наконец, последний вопрос, который поднимался в начале статьи: насколько оправданны жесткие карантинные меры, которые принимаются правительствами большинства стран мира?
Ежегодно в мире умирает около 58 миллионов человек. 2 миллиона, которые по пессимистическому прогнозу умрут от коронавируса, увеличат эту цифру на 3,5%. С другой стороны, масштабный мировой карантин грозит перерасти в самый большой экономический кризис со времен Великой депрессии. В результате без работы останутся десятки, а то и сотни миллионов людей. Доходы населения упадут, и многие умрут от голода или отсутствия возможности оплатить медицинскую помощь.
Часто высказываются мнения, в том числе и некоторыми мировыми лидерами, что лучше было бы предоставить людей своей судьбе, и не губить экономику. В конце концов, от сезонного гриппа ежегодно умирает от 300 до 650 тысяч человек, но никто не предпринимает столь разрушительные для экономики ограничительные меры.
Наша модель позволяет утверждать следующее: COVID-19 — это вовсе не сезонный грипп. Этот вирус несопоставимо более опасный. Дело в том, что точка перегиба логистической кривой существует не сама по себе. На нее очень сильно влияют условия протекания эпидемии. Ход течения любой эпидемии описывается логистической кривой, однако логистические кривые — это целое семейство. Мы помним, что точка перегиба расположена ровно в половине от максимума кривой. Поэтому, чем позже будет пройден пик смертности, тем больше будет финальное число умерших. Мы видели, что вблизи от точки перегиба логистическая кривая растет максимально быстро. Поэтому, если пик заболевания будет пройден на 10 дней позже, количество его жертв может увеличиться в несколько раз!
Полученные нами прогнозы по точкам перегиба логистических кривых уже включают в себя все карантинные меры, принятые правительствами стран мира. Если бы таких мер не было, то точки перегиба были достигнуты гораздо позже. В этом случае смертность могло бы достигнуть уровня 0,4–0,5% от всего населения земного шара.
Почему мы оцениваем уровень смертности от ничем не сдерживаемой эпидемии в 0,4–0,5% от населения. Мы предполагаем, что в этом случае в той или иной форме вирусом переболеет все население Земли. Однако у значительного числа людей болезнь пройдет в бессимптомной форме. Поэтому мы пользуемся статистикой таких стран, как Южная Корея и Германия, которым удалось организовать максимально широкое тестирование население на коронавирус, и выявить большинство реальных заболевших. В других странах, по нашему мнению, статистика искажена именно из-за того, что количество заболевших сильно занижено. Отсюда и сверхвысокие показатели смертности в 3,5%.
0,4–0,5% от населения Земли — это 28–35 миллионов человек. За все войны, которое вело человечество за всю свою историю, только число потерь во Второй мировой войне превосходит эту цифру. Тот факт, что правительства абсолютного большинства стран мира пошли на небывалые экономические жертвы ради спасения людей, показывает, насколько выросла в мире цена человеческой жизни. Насколько распространились идеи гуманизма и приоритета интересов личности. И это внушает автору гордость за человечество и надежду на лучшее будущее всего человечества.
Самый большой недостаток данной статьи
А вот и самый большой недостаток данной статьи. К сожалению, классическая статистика не дает нам инструментов для оценки погрешности прогнозов, построенных на основе логистической функции. Это связано с формой функции, которая имеет перегиб. Если бы этого перегиба не было, и кривая была бы монотонной, мы, с помощью преобразования Бокса-Кокса, сначала привели бы функцию к линейному виду. После этого, воспользовавшись уравнением погрешностей для линейной регрессии, построили бы верхнюю и нижнюю границу ошибок, а потом, с помощью обратного преобразования Бокса-Кокса, получили бы криволинейные границы ошибок, на основе которых построили бы максимальный и минимальный прогноз количества смертей от коронавируса.
Увы, инструменты классической статистики не дают возможности построить границы ошибок в случае кривой с перегибом. Но нам на помощь могут прийти методы машинного обучения. В следующей статье я покажу, как строятся границы ошибок в этом случае, и построю минимальный и максимальный прогнозы количества умерших как для каждой рассмотренной выше страны в отдельности, так и для всего мира.
А теперь много кода и цифр
Ну, а теперь, собственно, математика для тех, кто хочет понять, каким образом мы пришли к изложенным ранее выводам. Тем, кому не интересны занудные вычисления, можно дальше не читать.
Вычисления делались на языке Python в среде Jupiter с использованием дополнительных библиотек scipy, numpy, pandas, datetime. Для визуализации мы использовали пакет matplotlib.pyplot. Исходные данные о количестве умерших получены по этой ссылке и предварительно обработаны в Excel. Информация взята по состоянию на 4 апреля. Вот ссылка на файл с исходной информацией.
Итак, импортируем библиотеки, которые будем впоследствии использовать:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import pandas as pd
from IPython.display import display
import scipy as sp
from datetime import datetime
from scipy.optimize import minimize
Читаем исходные данные и преобразуем их в объект DataFrame. Метки переменных преобразуем в объект Timestamp. В принципе, можно было бы ограничиться простыми массивами numpy, но мы используем DataFrame для удобства хранения данных с соответствующей им датой, а Timestamp для визуализации, чтобы красиво отобразить эти даты на графиках.
corona = pd.read_csv ('D:/coronavirus.csv', sep=»;»)
corona.set_index ('Date', inplace=True)
corona.index = pd.to_datetime (corona.index)
Затем мы из единого объекта DataFrame создаем переменные типа Series, которые соответствуют общей смертности в каждой из стран. Х — это переменная, равная номеру дня от начала года. Она потребуется нам при прогнозировании.
X = corona['X']
chi = corona['China']
fr = corona['France']
ir = corona['Iran']
it = corona['Italy']
sp = corona['Spain']
uk = corona['UK']
us = corona['US']
bg = corona['Belgium']
gm = corona['Germany']
nt = corona['Netherlands']
sw = corona['Switzerland']
tot = corona['Total']
После этого рассчитываем простые массивы numpy для смертности в определенную дату. Заметим, что длина такого массива на 1 меньше, чем длина соответствующей ей переменной Series.
dchi = chi[1:].values - chi[:-1].values
dfr = fr[1:].values - fr[:-1].values
dit = it[1:].values - it[:-1].values
diran = ir[1:].values - ir[:-1].values
dsp = sp[1:].values - sp[:-1].values
duk = uk[1:].values - uk[:-1].values
dus = us[1:].values - us[:-1].values
dbg = bg[1:].values - bg[:-1].values
dgm = gm[1:].values - gm[:-1].values
dnt = nt[1:].values - nt[:-1].values
dsw = sw[1:].values - sw[:-1].values
dtot = tot[1:].values - tot[:-1].values
Вводим дополнительную переменную для прогнозирования. Это массив, который начинается 20 января, а заканчивается через 180 дней 17 июля. Также создаем соответствующий этому массиву объект Timestamp для подписи осей.
X_long = np.arange(20, 200)
time_long = pd.date_range('2020-01-20', periods=180)
Определяем функцию resLogistic, входным аргументом которой является массив из 3 цифр, а выходным –сумма квадратов разности между значениями логистической кривой и реальным количеством смертей от эпидемии в Китае.
def resLogistic(coefficents):
A0 = coefficents[0]
A1 = coefficents[1]
A2 = coefficents[2]
teor = A0 / (1 + np.exp(A1 * (X.ravel() - A2)))
return np.sum((teor - chi) ** 2)
Количество смертей берется на каждую дату накопленным итогом. Логистическая кривая определяется 3 компонентами входного вектора. Нулевая (счет элементов массивов в Python начинается с нуля) компонента отвечает за максимальное значение, первая характеризует скорость роста функции, вторая — положение точки перегиба на оси времени.
teor — значения количества смертей для каждого из дней, исходя из входного вектора параметров, chi — фактическое количество смертей в Китае. Функция возвращает сумму квадратов разностей между теоретическим и фактическим значением.
Теперь с помощью метода minimize библиотеки scipy.optimize находим вектор, который минимизирует сумму квадратов отклонений. Построенная на основе этого вектора логистическая кривая является искомым прогнозом смертности, сделанным на основе метода минимальных квадратов.
Добавим, что для метода minimize необходима исходная точка. Ее мы подбираем исходя из известных нам свойств логистической функции (максимум должен быть больше любого эмпирического числа смертей, а точка перегиба должна быть вблизи максимума кривой dtot, характеризующей количество новых смертей в день). Обычно результаты работы метода minimize не зависят от начальной точки, но встречаются исключения.
mimim.x — это значения минимизирующего вектора.
minim = minimize(resLogistic, [3200, -.16, 46])
minim.x
Теперь мы отображаем на графике фактическое количество смертей, аппроксимирующую его логистическую кривую прогноза, а также подписываем ось времени датами.
plt.figure(figsize=(15,10))
teorChi = minim.x[0] / (1 + np.exp(minim.x[1] * (X_long - minim.x[2])))
plt.plot(X,chi,'ro', label='Фактические данные')
plt.plot(X_long[:80], teorChi[:80],'b', label='Аппроксимация и прогноз')
plt.xticks(X_long[:80][::2], time_long.date[:80][::2], rotation='90');
plt.title('Количество умерших всего, Китай', Size=20);
plt.ylabel('Количество умерших человек')
plt.legend()
plt.grid()
На нижнем графике мы строим первую производную от подобранной выше логистической кривой (синяя линия), а также реальную кривую новых смертей (красная линия).
plt.figure(figsize = (15,10))
plt.grid()
plt.title('Количество новых смертей в день, Китай', Size=20);
plt.plot(X[1:], dchi, 'r', Marker='o', label='Фактические данные')
plt.xticks(X_long[1:120][::3], time_long.date[1:120][::3], rotation='90');
plt.plot(X_long[1:120], teorChi[1:120] - teorChi[:119],'b', label='Аппроксимация и прогноз')
plt.ylabel('Количество умерших человек')
plt.legend()
Аналогичные вычисления проводим для каждой из упомянутых в статье стран.
Тут автор написал не очень красивый код. Нужно было написать одну функцию для всех стран и передавать ей количество реальных смертей через параметры метода minimize. Но у автора не было времени разбираться с этим механизмом, поэтому он написал для каждой страны свою функцию, а внутрь функции заложил обращение к переменной, содержащей информацию о количестве смертей в данной стране.
Ниже представлены расчеты для Ирана, Италии, Испании, США. Восстановить расчеты для других стран, у читателей, думаю, не составит труда.
def resLogisticIr(coefficents):
A0 = coefficents[0]
A1 = coefficents[1]
A2 = coefficents[2]
teor = A0 / (1 + np.exp(A1 * (X.ravel() - A2)))
return np.sum((teor - ir) ** 2)minim = minimize(resLogisticIr, [3200, -.16, 80])
minim.xplt.figure(figsize=(15,10))
teorIr = minim.x[0] / (1 + np.exp(minim.x[1] * (X_long - minim.x[2])))
plt.plot(X_long[:120], teorIr[:120],'b', label='Аппроксимация и прогноз')
plt.xticks(X_long[:120][::3], time_long.date[:120][::3], rotation='90');
plt.title('Количество умерших всего, Иран', Size=20);
plt.plot(X,ir,'ro', label='Фактические данные')
plt.grid()
plt.legend()
plt.ylabel('Количество умерших человек')
plt.figure(figsize = (15,10))
plt.grid()
plt.title('Количество новых смертей в день, Иран', Size=20);
plt.plot(X[1:], diran, 'r', Marker='o', label='Фактические данные')
plt.plot(X[1:], diran, 'ro')
plt.xticks(X_long[1:120][::3], time_long.date[1:120][::3], rotation='90');
plt.plot(X_long[1:120], teorIr[1:120] - teorIr[:119],'b', label='Аппроксимация и прогноз')
plt.ylabel('Количество умерших человек')
plt.legend()
def resLogisticIt(coefficents):
A0 = coefficents[0]
A1 = coefficents[1]
A2 = coefficents[2]
teor = A0 / (1 + np.exp(A1 * (X.ravel() - A2)))
return np.sum((teor - it) ** 2)minim = minimize(resLogisticIt, [3200, -.16, 46])
minim.xplt.figure(figsize=(15,10))
teorIt = minim.x[0] / (1 + np.exp(minim.x[1] * (X_long - minim.x[2])))
plt.plot(X,it,'ro', label='Фактические данные')
plt.plot(X_long[:120], teorIt[:120],'b', label='Аппроксимация и прогноз')
plt.xticks(X_long[:120][::3], time_long.date[:120][::3], rotation='90');
plt.title('Количество умерших всего, Италия', Size=20);
plt.ylabel('Количество умерших человек')
plt.grid()
plt.legend()

plt.figure(figsize = (15,10))
plt.grid()
plt.title('Количество новых смертей в день, Италия', Size=20);
plt.plot(X[1:], dit, 'r', Marker='o', label='Фактические данные')
plt.xticks(X_long[1:120][::3], time_long.date[1:120][::3], rotation='90');
plt.plot(X_long[1:120], teorIt[1:120] - teorIt[:119],'b', label='Аппроксимация и прогноз')
plt.ylabel('Количество умерших человек')
plt.legend()
def resLogisticSp(coefficents):
A0 = coefficents[0]
A1 = coefficents[1]
A2 = coefficents[2]
teor = A0 / (1 + np.exp(A1 * (X.ravel() - A2)))
return np.sum((teor - sp) ** 2)minim = minimize(resLogisticSp, [3200, -.16, 80])
minim.xplt.figure(figsize=(15,10))
teorSp = minim.x[0] / (1 + np.exp(minim.x[1] * (X_long - minim.x[2])))
plt.plot(X_long[:120], teorSp[:120],'b', label='Аппроксимация и прогноз')
plt.xticks(X_long[:120][::3], time_long.date[:120][::3], rotation='90');
plt.title('Количество умерших всего, Испания', Size=20);
plt.plot(X,sp,'ro', label='Фактические данные')
plt.grid()
plt.legend()
plt.ylabel('Количество умерших человек')
plt.figure(figsize = (15,10))
plt.grid()
plt.plot(X[1:], dsp, 'r', Marker='o', label='Фактические данные')
plt.plot(X[1:], dsp, 'ro')
plt.xticks(X_long[1:120][::3], time_long.date[1:120][::3], rotation='90');
plt.title('Количество новых смертей в день, Испания', Size=20);
plt.plot(X_long[1:120], teorSp[1:120] - teorSp[:119],'b', label='Аппроксимация и прогноз')
plt.ylabel('Количество умерших человек')
plt.legend()
def resLogisticUs(coefficents):
A0 = coefficents[0]
A1 = coefficents[1]
A2 = coefficents[2]
teor = A0 / (1 + np.exp(A1 * (X.ravel() - A2)))
return np.sum((teor - us) ** 2)minim = minimize(resLogisticUs, [3200, -.16, 100])
minim.xplt.figure(figsize=(15,10))
teorUS = minim.x[0] / (1 + np.exp(minim.x[1] * (X_long - minim.x[2])))
plt.plot(X_long[:120], teorUS[:120],'b', label='Аппроксимация и прогноз')
plt.xticks(X_long[:120][::3], time_long.date[:120][::3], rotation='90');
plt.title('Количество умерших всего, США', Size=20);
plt.plot(X,us,'ro', label='Фактические данные')
plt.grid()
plt.legend()
plt.ylabel('Количество умерших человек')
plt.figure(figsize = (15,10))
plt.grid()
plt.title('Количество новых смертей в день, США', Size=20);
plt.plot(X[1:], dus, 'r', Marker='o', label='Фактические данные')
plt.plot(X[1:], dus, 'ro')
plt.xticks(X_long[1:120][::3], time_long.date[1:120][::3], rotation='90');
plt.plot(X_long[1:120], teorUS[1:120] - teorUS[:119],'b', label='Аппроксимация и прогноз')
plt.ylabel('Количество умерших человек')
plt.legend()
