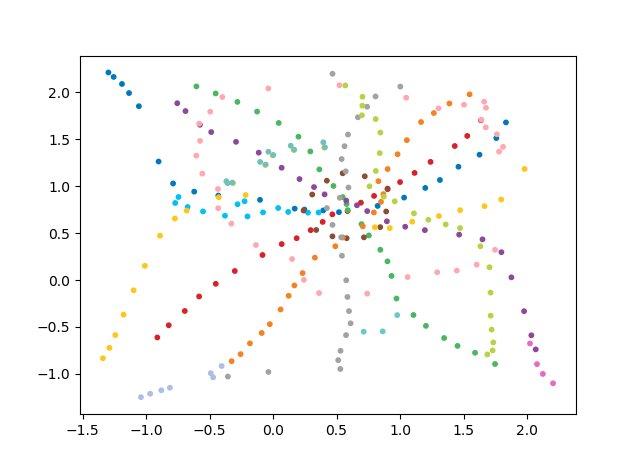
[Из песочницы] Как выглядело бы Московское метро в трехмерном мире
Добрый день! Недавно я читал блог одного урбаниста, который рассуждал о том, какая должна быть идеальная схема метро.Схему метро можно рисовать исходя из двух принципов:
- Схема должна быть удобной и простой для запоминания и ориентирования
- Схема должна соответствовать географии города
Очевидно, что эти принципы взаимоисключающие и первый принцип требует существенного искажения географической реальности.
Достаточно вспомнить, как выглядит схема Московского метро с красивыми кольцами и прямыми линиями: 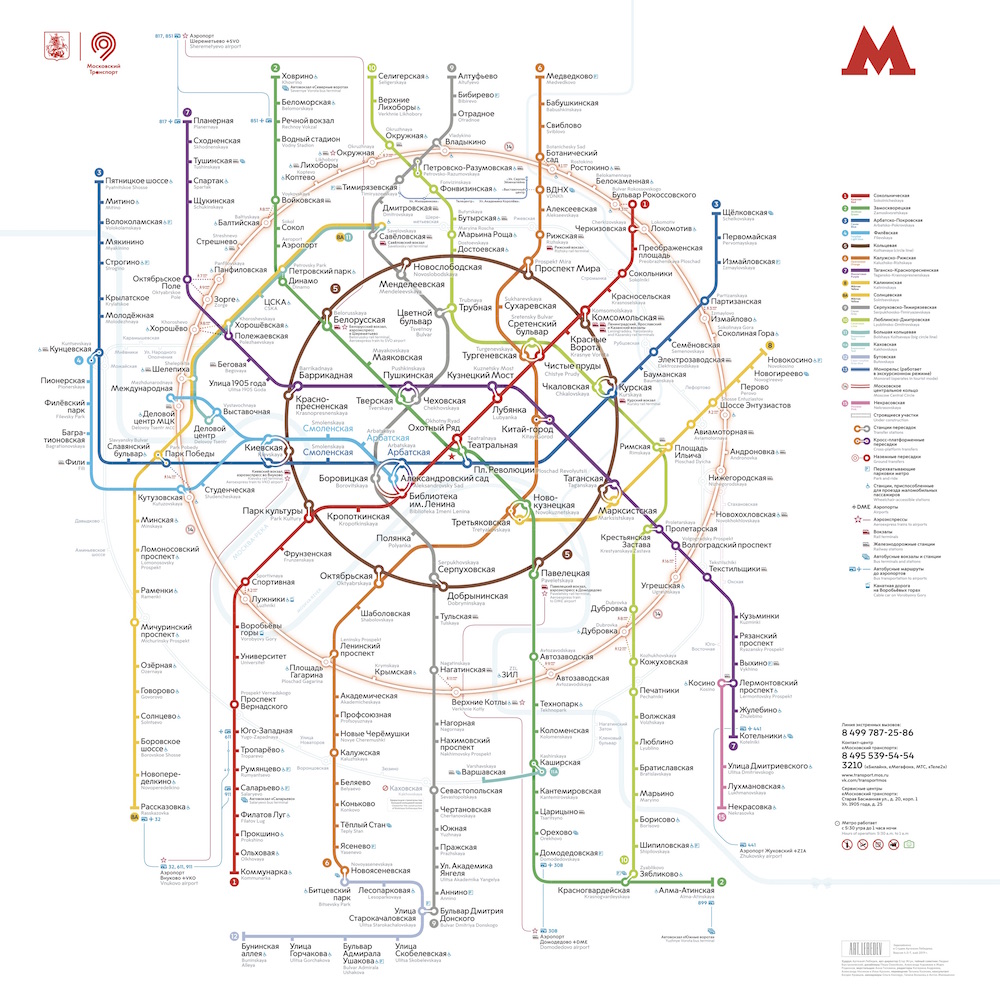
и сравнить с географически точным планом:

На плане видно что кольца вовсе не являются идеально ровными и концентрическими, линии изгибаются гораздо сильнее, чем в схеме, а плотность станций в центре города настолько велика, что в плане практически невозможно разобраться.
И хотя второе изображение гораздо точнее отображает реальность, видно, что пользоваться для планирования маршрута в метро удобнее первой схемой.
И тут мне в голову пришла следующая мысль: «Как выглядело бы метро, если бы критерием для построения схемы являлось время, требуемое для перемещения от одной станции к другой?». То есть если от одной станции до другой добраться быстро, то пространственно они на схеме располагались бы недалеко.
Очевидно, что в двумерном пространстве невозможно нарисовать такую схему, в которой расстояние между двумя станциями равнялось бы времени путешествия от одной к другой из-за сложной топологии графа метро.
Также есть догадка, что такое точно возможно при построении схемы в пространстве с высокой размерностью (верхняя оценка n-1, где n- число станций). Для пространства с небольшим количеством измерений такую схему можно построить лишь приближенно.
Задача построения карты метро по времени путешествия выглядит типичной задачей оптимизации.
Пусть у нас есть начальный набор координат всех станций (X, Y, Z) и целевая матрица попарных времен (расстояний). Можно сконструировать метрику «неправильность» данного набора координат и далее минимизировать ее методом градиентного спуска по каждой из координат каждой станции. В качестве метрики можно взять простую функцию среднеквадратичного отклонения расстояний.
Что же, осталось дело за малым — нужно получить данные о том, сколько времени следует затратить на путешествие от любой станции московского метро к любой другой.
Первой мыслью было проверить api яндекс метро и вытащить оттуда эти данные. К сожалению, описания api и найти не удалось. Смотреть времена вручную в приложении долго (в метро 268 станций и размер матрицы времен 268×268=71824). Поэтому я решил разобраться в исходных данных Яндекс Метро. Так как доступа к серверу нет, был скачан apk файл с приложением и обнаружены необходимые данные. Вся информация о метро замечательно структурирована и хранится в формате JSON в папке assets/metrokit/ apk-архива приложения. Все данные хранятся в self-explanotary структурах. Meta.json содержит информацию о городах, схемы которых присутствуют в приложении, а также id данных схем.
{
"id": "sc77792237",
"name": {
"en": "Nizhny Novgorod",
"ru": "Нижний Новгород",
"tr": "Nizhny Novgorod",
"uk": "Нижній Новгород"
},
"size": {
"packed": 30300,
"unpacked": 145408
},
"tags": [
"published"
],
"aliases": [
"nizhny-novgorod"
],
"logoUrl": "https://avatars.mds.yandex.net/get-bunker/135516/f2f0e33d8def90c56c189cfb57a8e6403b5a441c/orig",
"version": "2c27fe1",
"geoRegion": {
"delta": {
"lat": 0.168291,
"lon": 0.219727
},
"center": {
"lat": 56.326635,
"lon": 43.992153
}
},
"countryCode": "RU",
"defaultAlias": "nizhny-novgorod"
}
По id схемы находим папку с JSON, относящиеся и к Москве.
Файл data.json содержит основную информацию о графе метро, включая названия узлов графа, id узлов, географические координаты узлов, информацию о переходах с одной станции на другую (id, время перехода, тип перехода — перегон или пешком, по улицу или нет, время интересующее нас в секундах), а также много дополнительной информации о входах и выходах со станции. С этим достаточно легко разобраться. Начнем писать код для построения нашей схемы.
Импортируем необходимые библиотеки:
import numpy as np
import json
import codecs
import networkx as nx
import matplotlib.pyplot as plt
import pandas as pd
import itertools
import keras
import keras.backend as K
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.proj3d import proj_transform
from matplotlib.text import Annotation
import pickle
Структура словарей и списков python полностью соответствует структуре формата json, поэтому читаем иннформацию о метро и создаем объекты, соответствующие json объектам.
names = json.loads(codecs.open( "l10n.json", "r", "utf_8_sig" ).read() )
graph = json.loads(codecs.open( "data.json", "r", "utf_8_sig" ).read() )
Создаем словарь, ставящий в соответствие узлы графа и станции (это необходима для так как к именам привязаны именно станции, а не узлы графа)
Также на всякий случай сохраним координаты узлов для возможности построения географической карты (нормированы на диапазон 0–1)
nodeStdict={}
for stop in graph['stops']['items']:
nodeStdict[stop['nodeId']]=stop['stationId']
coordDict={}
for node in graph['nodes']['items']:
coordDict[node['id']]=(node['attributes']['geoPoint']['lon'],node['attributes']['geoPoint']['lat'])
lats=[]
longs=[]
for value in coordDict.values():
lats.append(value[1])
longs.append(value[0])
for k,v in coordDict.items():
coordDict[k]=((v[0]-np.min(longs))/(np.max(longs)-np.min(longs)),(v[1]-np.min(lats))/(np.max(lats)-np.min(lats)))
Создадим граф метро со связями. Зададим веса каждой связи. Вес соответствует времени в пути. Удалим узлы, не являющиеся станциями (по-моему это выходы из метро, а связи к ним нужны для яндекс карт при расчете времени, но точно не разбирался) создадим словарь id узла- реальное название на русском языке
G=nx.Graph()
for node in graph['nodes']['items']:
G.add_node(node['id'])
#graph['links']
for link in graph['links']['items']:
#G.add_edges_from([(link['fromNodeId'],link['toNodeId'])])
G.add_edge(link['fromNodeId'], link['toNodeId'], length=link['attributes']['time'])
nodestoremove=[]
for node in G.nodes():
if len(G.edges(node))<2:
nodestoremove.append(node)
for node in nodestoremove:
G.remove_node(node)
labels={}
for node in G.nodes():
try:
labels[node]=names['keysets']['generated'][nodeStdict[node]+'-name']['ru']
except: labels[node]='error'
Определим к какой ветке (к какому id ветки) относится каждый узел (это понадобится позже для раскрашивания линий метро на схеме)
def getlines(graph, G):
nodetoline={}
id_from={}
id_to={}
for lk in graph['tracks']['items']:
id_from[lk['id']]=lk['fromNodeId']
id_to[lk['id']]=lk['toNodeId']
for line in graph['linesToTracks']['items']:
if line['trackId'] in id_from.keys():
nodetoline[id_from[line['trackId']]]=line['lineId']
nodetoline[id_to[line['trackId']]]=line['lineId']
return nodetoline
lines=getlines(graph,G)
библиотека networkx позволяет найти длину кратчайшего пути от одного узла к другому при помощи функции nx.shortest_path_length (G, id1, id2, weight='length'), поэтому можно считать что с подготовкой данных закончили. Следующее, что необходимо сделать — подготовить модель, которая будет оптимизировать координаты станций.
Для этого разберемяся, что будет даваться на вход, на выход и как будем оптимизировать матрицу координат станций.
Предположим, у нас есть матрица всех координат (3×268). Умножение one-hot вектора (вектора, где везде 0, кроме одной единичной координаты на месте n) размерности 268 на данную матрицу координат даст 3 координаты, соответствующие станции n. Если мы возьмем пару one-hot векторов и умножим их на необходимую матрицу, то получим две тройки координат. Из пары координат можно расчитать евклидово расстояние между станциями. Таким образом, можно определить архитектуру нашей модели:
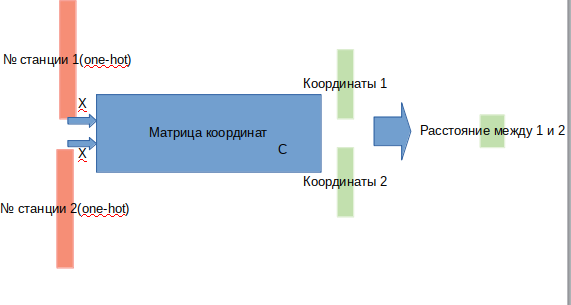
на вход мы подаем пару станций, на выходе получаем расстояние между ними.
После того, как мы определились с форматом данных для обучения модели, подготовим данные с использованием поиска расстояний на графе:
myIDs=list(G.nodes())
listofinputs1=[]
listofinputs2=[]
listofoutputs=[]
for pair in itertools.product(G.nodes(), repeat=2):
vec1=np.zeros((len(myIDs)))
vec2=np.zeros((len(myIDs)))
vec1[myIDs.index(pair[0])]=1
vec2[myIDs.index(pair[1])]=1
listofinputs1.append(vec1)
listofinputs2.append(vec2)
#listofinputs.append([vec1,vec2])
listofoutputs.append(nx.shortest_path_length(G, pair[0], pair[1], weight='length')/3600)
#myDistMatrix[myIDs.index(pair[0]),myIDs.index(pair[1])]=nx.shortest_path_length(G, pair[0], pair[1], weight='length')
Оптимизируем методом градиентного спуска матрицу координат станций.
Если мы будем использовать фреймворк keras для машинного обучения, то получим следующее:
np.random.seed(0)
initweightmatrix=np.zeros((len(myIDs),3))
for i in range(len(myIDs)):
initweightmatrix[i,:2]=coordDict[myIDs[i]]
initweightmatrix[i,2]=np.random.randn()*0.001
def euclidean_distance(vects):
x, y = vects
sum_square = K.sum(K.square(x - y), axis=1, keepdims=True)
return K.sqrt(K.maximum(sum_square, K.epsilon()))
def eucl_dist_output_shape(shapes):
shape1, shape2 = shapes
return (shape1[0], 1)
inp1=keras.layers.Input((len(myIDs),))
inp2=keras.layers.Input((len(myIDs),))
layer1=keras.layers.Dense(3,use_bias=None, activation=None)
x1=layer1(inp1)
x2=layer1(inp2)
x=keras.layers.Lambda(euclidean_distance,
output_shape=eucl_dist_output_shape)([x1, x2])
out=keras.layers.Dense(1,use_bias=None,activation=None)(x)
model=keras.Model(inputs=[inp1,inp2],outputs=out)
model.layers[2].set_weights([initweightmatrix])
model.layers[2].trainable=False
model.compile(optimizer=keras.optimizers.Adam(lr=0.01), loss='mse')
заметим, что в качестве начальных координат в слое layer1 мы используем реальные географические координаты -это необходимо для того, чтобы не попасть в локальный минимум функции СКО. Третью координату инициализируем ненулевой для получения ненулевого градиента (если в начале карта будет абсолютно плоской, смещение любой станции вверх или вниз будет равнозначно, следовательно градиент равен 0 и оптимизации z не произойдет). Последний элемент нашей модели (Dense (1)) влияет на масштабирование схемы для соответствия временной шкале.
Расстояние будем измерять в часах, а не секундах, так как порядки расстояний — около 1 часа, а для более эффективного обучении модели важно, чтобы все величины (входные данные, веса, targetы) были примерно одного порядка по величине. Если эти значения близки к 1, то можно использовать стандартные значения шага при оптимизации (0.001–0.01).
Строка model.layers[2].trainable=False замораживает координаты станций и на первом этапе варьируется один параметр — масштаб. После подбора масштаба нашей схемы размораживаем координаты и оптимизируем уже их:
hist=model.fit([listofinputs1,listofinputs2],listofoutputs,batch_size=71824,epochs=200)
model.layers[2].trainable=True
model.layers[-1].trainable=False
model.compile(optimizer=keras.optimizers.Adam(lr=0.01), loss='mse')
hist2=model.fit([listofinputs1,listofinputs2],listofoutputs,batch_size=71824,epochs=200)
видим, что на вход подаем сразу все пары станций, на выходе — все расстояния и наша оптимизация- full batch gradient descent (один шаг на всех данных). Функция loss в данном случае — среднеквадратичное отклонение и можно видеть, что оно составило 0.015 в конце обучения, что значит среднеквадратичное отклонение менее чем в 1 минуты для любой пары станций. Иными словами, полученная схема позволяет точно узнать расстояние, которое требуется, чтобы добраться от одной станции к другой по расстоянию по прямой между станциями сточностью ±1 минута!
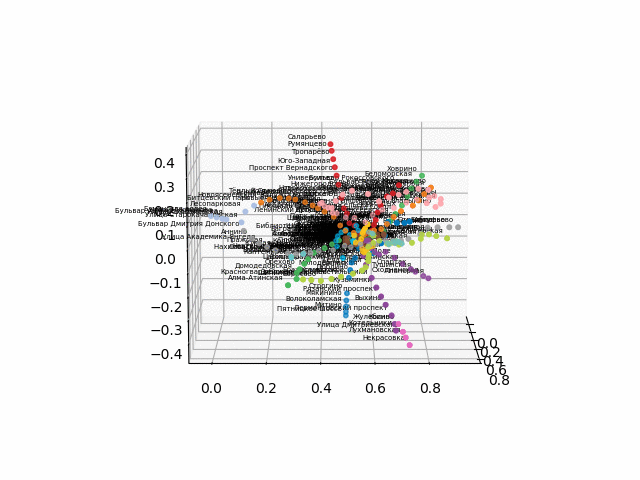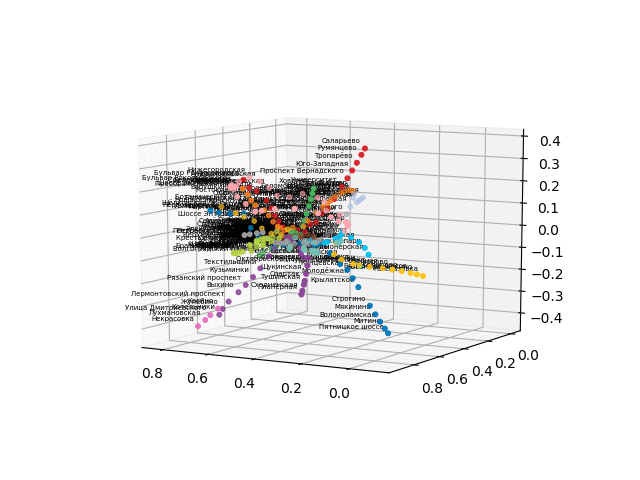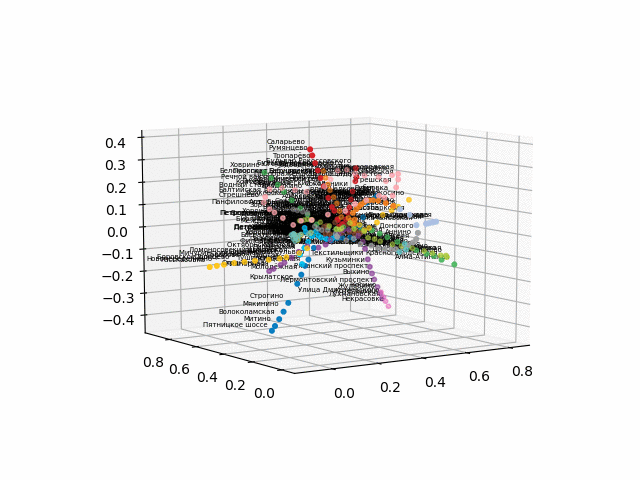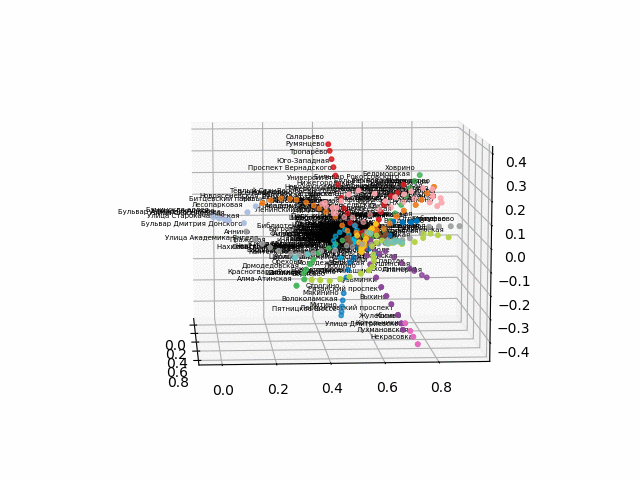
Но давайте посмотрим, как выглядит наша схема!
получим координаты станций, возьмем цветовую кодировку линий и построим 3d изображение с подписями (код для красивого отображения подписей взят отсюда):
class Annotation3D(Annotation):
'''Annotate the point xyz with text s'''
def __init__(self, s, xyz, *args, **kwargs):
Annotation.__init__(self,s, xy=(0,0), *args, **kwargs)
self._verts3d = xyz
def draw(self, renderer):
xs3d, ys3d, zs3d = self._verts3d
xs, ys, zs = proj_transform(xs3d, ys3d, zs3d, renderer.M)
self.xy=(xs,ys)
Annotation.draw(self, renderer)
def annotate3D(ax, s, *args, **kwargs):
'''add anotation text s to to Axes3d ax'''
tag = Annotation3D(s, *args, **kwargs)
ax.add_artist(tag)
fincoords=model.layers[2].get_weights()
ccode={}
for obj in graph['services']['items']:
ccode[obj['id']]=('\#'+obj['attributes']['color'])[1:]
xn = fincoords[0][:,0]
yn = fincoords[0][:,1]
zn = fincoords[0][:,2]
l=[labels[idi] for idi in myIDs]
colors=[ccode[lines[idi]] for idi in myIDs]
xyzn = zip(xn, yn, zn)
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.scatter(xn,yn,zn, c=colors, marker='o')
for j, xyz_ in enumerate(xyzn):
annotate3D(ax, s=labels[myIDs[j]], xyz=xyz_, fontsize=9, xytext=(-3,3),
textcoords='offset points', ha='right',va='bottom')
plt.show()
Так как возникли трудности с конвертацией в интерактивный 3d формат для браузера, выкладываю гифки:
более красиво и узнаваемо выглядит версия без текста:
xn = fincoords[0][:,0]
yn = fincoords[0][:,1]
zn = fincoords[0][:,2]
l=[labels[idi] for idi in myIDs]
colors=[ccode[lines[idi]] for idi in myIDs]
xyzn = zip(xn, yn, zn)
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.scatter(xn,yn,zn, c=colors, marker='o')
plt.show()
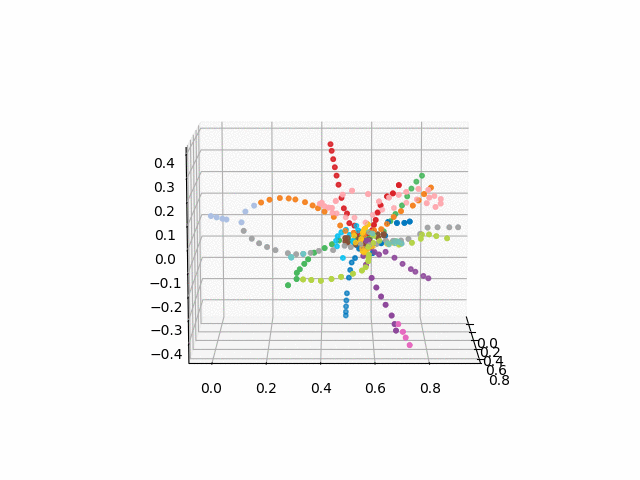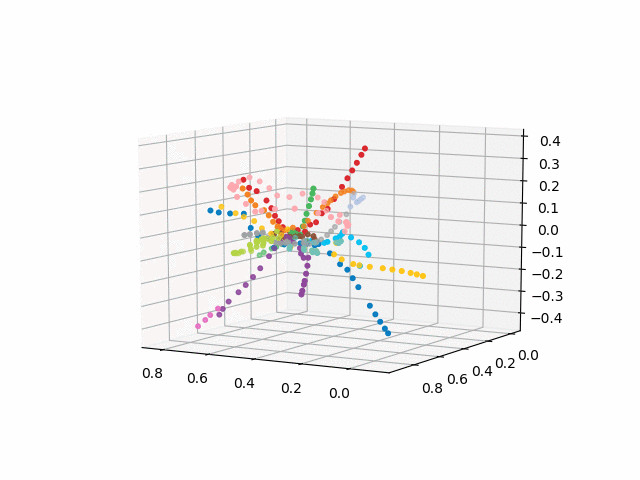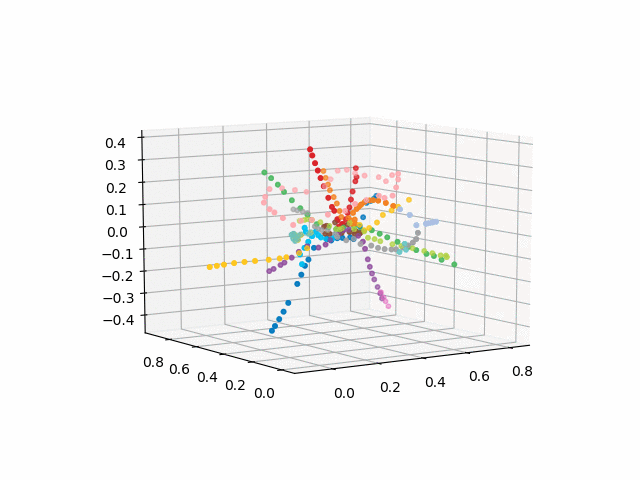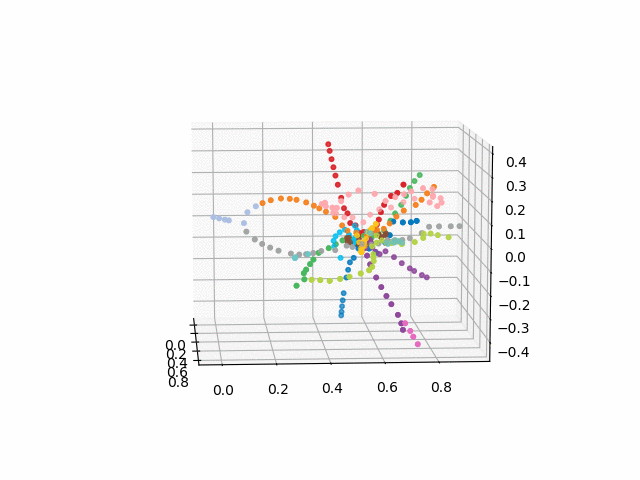
Из данной схемы можно сделать некоторые интересные выводы, которые не столь очевидны из других схем. Для некоторых веток, например зеленой, синей или фиолетовой МЦК (розовое кольцо) практически бесполезно из-за неудобных пересадок, что видно в удалении кольца от этих веток. Самые длинные по времени маршруты — от коммунарки до щелкого или пятницкого шоссе (коней красной и розовая/синяя линии) длинные маршруты так же алмаатинская-рассказовка и бунинская аллея-некрасовка. На севере москвы, судя по плану, происходит частичное дублирование Серой и салатовой ветками — они находятся рядом в пространстве времен путешествий. Было бы итересно посмоотреть на то, как новые линии (МЦД, БКЛ) и кто чаще будет пользоваться ими. В любом случае, надеюсь, подобные схемы могут быть интересным инструментам анализа, вдохновения и планирования поездок.
P.S. 3D не обязательно, для 2D варианта достаточно чуть-чуть исправить код. Но в случае 2d схемы добиться подобной точности расстояний невозможно.