[Из песочницы] Изобретаем велосипед или пишем персептрон на С++. Часть 1 и 2
Напишем простую библиотеку для реализации персептрона на C++

Вступление
Всем привет, в этом посте я хочу поделиться с вами моим первым опытом в написании нейросетей. Статей о реализации нейросетей (НС в дальнейшем), достаточно много в интернете, но использовать чужие алгоритмы без понимания сути их работы я не хочу, поэтому решил создавать собственный код с нуля.
В этой части я опишу основные моменты мат. части, которые нам пригодятся. Вся теория взята с разных сайтов, в основном с википедии.
Итак, поехали.
Немного теории
Давайте договоримся, что я не претендую на звание «самый лучший алгоритм машинного обучения», я просто показываю свою реализацию и свои идеи. Также я всегда открыт для конструктивной критики и советов по коду, это важно, для этого и существует сообщество.
Изучив виды нейросетей на википедии, я выбрал персептрон для первого проекта благодаря простоте работы и относительной простоте реализации. Для начала вспомним как схематично выглядит персептрон

Как мы видим каждый нейрон слоя связан с каждым нейроном предыдущего слоя. А каждый узел этой сети будет называться нейроном.
Теперь рассмотрим работу каждого узла отдельно. Данная картинка как нельзя лучше передаёт смысл каждого нейрона:
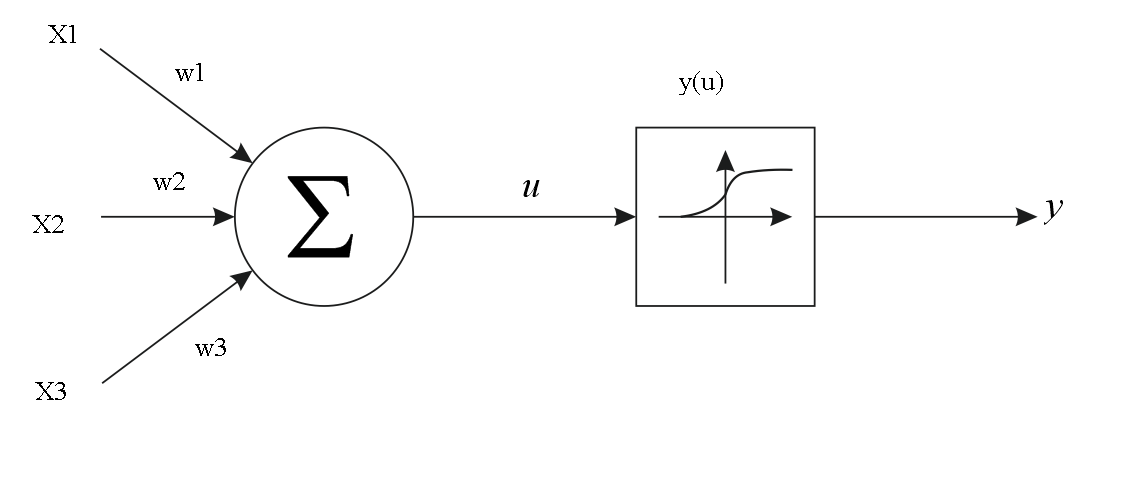
Допустим, что в наш нейрон приходят три сигнала (х1, х2, х3), тогда для вычисления значения u нейрон складывает произведения входных сигналов на веса входов (w1, w2, w3), или проще говоря:
u = x1*w1 + x2*w2 + x3*w3
В более общем виде выражение записывается так:

Теперь поговорим об активационной функции нейрона. На рисунке она указана как y (u), где u — уже известная нам величина. Эта функция нужна для вычисления значения, которое будет на выходе нейрона и пойдёт на входы других нейронов.
Активационной функцией может быть любая функция, имеющая предел, т.е значении, к которому она стремится, но никогда не достигнет. Таких функций огромное множество, но мы воспользуемся наиболее популярной — сигмоидой (кстати, изображена на рисунке). Вот так она выглядит в контексте наших переменных:

Данное чудо ограничено диапазоном значений (0; 1), поэтому отлично нам подходит. А величина y (u) будет называться выходным значением нейрона.
Фух, ну вроде с минимальной мат. частью разобрались, теперь приступим к практике.
На листе бумаги всё выглядит просто замечательно, но когда дело дошло до написания кода, то возник вопрос с хранением значений нейронов.
При использовании НС по назначению проблема не серьёзная, можно было бы легко запоминать промежуточные вычисления и шагать буквально по слоям сети. Однако во время обучения НС нам необходимо запоминать абсолютно всё, что происходит в сети, в том числе и ошибку каждого нейрона (об обучении и его тонкостях расскажу в следующей части статьи).
Итак, для решения проблемы хранения данных предлагаю использовать 2 трёхмерных массива: один для хранения нужных значений нейрона, второй для хранения значений весов каждой связи.
Объясню идею на картинках:
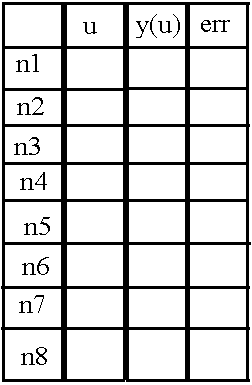
Пусть у нас есть 8 нейронов в слое (с n1 по n8), а мы хотим хранить значения той самой суммы произведений u, вычисленного из сигмоиды значения «y (u)» и ошибки «err», тогда воспользуемся двумерным массивом (матрицей). Смысл поля «err» поясню в следующей части.
Но такой вариант подходит лишь для одного слоя, а слоёв в сети немногим больше, чем один.
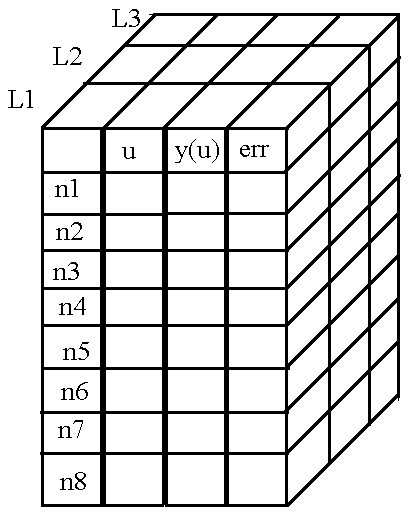
Тогда на помощь к нам приходит третье измерение массива, а номер матрицы отдельного слоя и будет номером этого слоя.
Здесь стоит сделать отступление. Можно круто оптимизировать код, объявив одномерный массив вместо трёхмерного массива, для этого нужно написать функцию, которая будет работать с памятью. Но тут мы пишем простой код, поэтому оптимизацию не будем сильно затрагивать в этой части статьи.
Ну вроде принципы хранения нужных значений в нейронах получилось объяснить. Теперь разберёмся с хранением весов связей между нейронами.
Возьмём для примера вот такую сеть:
.
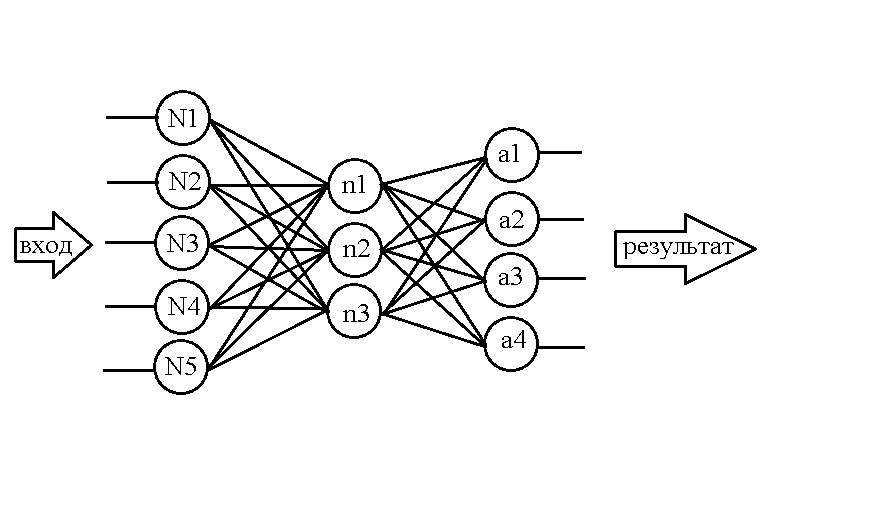
Уже зная, как структурировать в памяти нейроны, сделаем подобную таблицу для весов:

Её структура совсем не сложная: например, значение веса между нейроном N1 и нейроном n1 содержится в ячейке w1–1, аналогично и с другими весами. Но опять же, такая матрица пригодна для хранения весов только между двумя первыми слоями, но ведь в сети есть ещё веса между вторым и третьим слоями. Воспользуемся уже знакомым приёмом — добавим новое измерение в массив, но с оговоркой: пускай названия строчек отображают слой нейронов слева относительно «пучка» весов, а слой нейронов справа вписывается в названия столбцов.
Тогда получим для второго «пучка» весов такую таблицу:
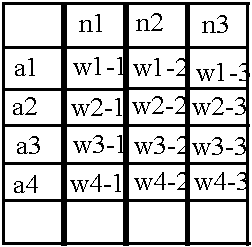
А всё пространство весов теперь будет выглядеть так:
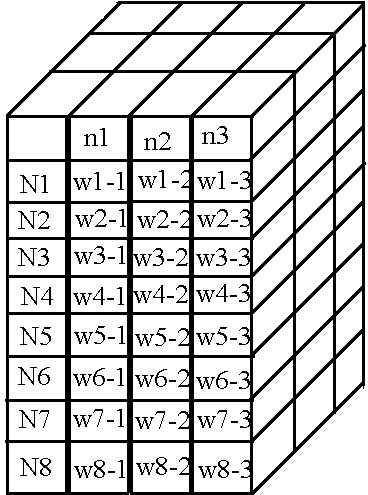
При таком хранении весов и вычислений нейронов возникает проблема высокого расхода памяти «впустую», т.к. количество нейронов на слоях может быть абсолютно любым, но массивы, которые мы делаем «имеют форму» параллелепипеда, из-за чего возникает большое количество пустых ячеек, но под которые резервируется память. Именно поэтому я не считаю свой алгоритм наиболее оптимальным и хотелось бы увидеть ваши предложения по оптимизации в комментариях)).
И в заключение первой части
А на этом первая часть заканчивается, во второй части разберём программную реализацию.
В этой части программно реализуем идеи, описанные в прошлый раз.
Вступление
В предыдущей части я представил на ваш суд несколько идей, которые позволят реализовать персептрон. На этот раз мы будем писать код.
Итак, поехали!
Оформление header — файла
Дабы наш код можно было использовать в различных проектах, оформим его как библиотеку. Для этого создадим header — файл (пусть называется «neuro.h»). Внутри него опишем класс с основными методами:
class NeuralNet {
public:
NeuralNet(uint8_t L, uint16_t *n);
void Do_it(uint16_t size, double *data);
void getResult(uint16_t size, double* data);
void learnBackpropagation(double* data, double* ans, double acs, double k);
private:
vector>> neurons;
vector>> weights;
uint8_t numLayers;
vector neuronsInLayers;
double Func(double in);
double Func_p(double in);
uint32_t MaxEl(uint16_t size, uint16_t *arr);
void CreateNeurons(uint8_t L, uint16_t *n);
void CreateWeights(uint8_t L, uint16_t *n);
}; Работать будем с векторами, поэтому впишем несколько строк для их работы, но и про стандартную обвязку header’а не забудем). Вставим в начало файла следующие строки:
//строки ниже нужны, чтобы сказать предпроцессору о компиляции этого файла, если ранее он не был упомянут в коде
#ifndef NEURO_H
#define NEURO_H
#include //файл для работы с векторами
#include //библиотека для работы с математикой, нужна для объявления активационной функции
#include //эта библиотека позволит использовать более оптимизированные типы данных, что немного сократит объём выделяемой памяти для нашего не самого оптимизированного кода.
Разберёмся с публичными функциями класса:
NeuralNet(uint8_t L, uint16_t *n);Функция представляет собой просто конструктор класса, в который мы будем передавать данные о НС, а именно кол-во слоёв и количество нейронов в каждом из этих слоёв в виде массива.
void Do_it(uint16_t size, double *data);Не долго думал над названием этой функции)), но именно она отвечает за прямое распространение исходных данных по сети.
void getResult(uint16_t size, double* data);Эта функция позволяет получить выходные данные с последнего слоя сети.
void learnBackpropagation(double* data, double* ans, double acs, double k);Благодаря этой процедуре можно обучить нейросеть, используя метод обратного распространения ошибки.
На этом публичные методы класса заканчиваются, сейчас остановимся на приватных полях класса:
vector>> neurons; //трёхмерный вектор с нейронами, который мы описывали ранее
vector>> weights; //трёхмерный вектор с весами, его мы тоже описали в первой части
uint8_t numLayers; //количество слоёв сети
vector neuronsInLayers; //вектор, хранящий количество нейронов на каждом слое
/*
Вообще это поле и предыдущее можно было бы и не объявлять, а брать количество слоёв и нейронов, исходя из размеров пространств весов и нейронов, но в этой статье мы не сильно затрагиваем вопросы оптимизации, этим займёмся позже
*/
double Func(double in); // та самая активационная функция
double Func_p(double in); // производная той самой активационной функции
uint32_t MaxEl(uint16_t size, uint16_t *arr);// простенькая функция для поиска максимума в массиве
void CreateNeurons(uint8_t L, uint16_t *n);// эту и следующую функции использует конструктор для разметки векторов с весами и нейронами
void CreateWeights(uint8_t L, uint16_t *n);
Закончим header — файл строкой:
#endifНа этом завершим header и оставим его в покое. Переходим к самому вкусному — source — файлу).
Код внутри source — файла
Ссылка на весь код будет в конце, мы же разберём самые интересные его места.
Конструктор класса изнутри выглядит так:
NeuralNet::NeuralNet(uint8_t L, uint16_t *n) {
CreateNeurons(L, n); //переразмечаем пространство нейронов
CreateWeights(L, n); //переразмечаем пространство весов
this->numLayers = L;
this->neuronsInLayers.resize(L);
for (uint8_t l = 0; l < L; l++)this->neuronsInLayers[l] = n[l]; //в последних трёх строках заполняем все переменные класса
}
Про функцию прямого распространения рассказать особо нечего, просто берём и считаем всё от слоя к слою:
void NeuralNet::Do_it(uint16_t size, double *data) {
for (int n = 0; n < size; n++) { // тут вносим данные в нейроны первого слоя
neurons[n][0][0] = data[n]; // нулевое место отвечает за хранение входного значения
neurons[n][1][0] = Func(neurons[n][0][0]); // первое место отвечает за значение функции от входного в нейрон значения
}
for (int L = 1; L < numLayers; L++) { // а здесь от слоя к слою считаем входные значения каждого нейрона и значения их активационных функций
for (int N = 0; N < neuronsInLayers[L]; N++) {
double input = 0;
for (int lastN = 0; lastN < neuronsInLayers[L - 1]; lastN++) {// для каждого отдельного нейрона подсчитаем сумму его входов для отправки в активационную функцию
input += neurons[lastN][1][L - 1] * weights[lastN][N][L - 1];
}
neurons[N][0][L] = input;
neurons[N][1][L] = Func(input);
}
}
}
И, наконец, последнее, о чём хотелось бы рассказать, это функция вывода результата. Ну тут мы просто копируем значения из нейронов последнего слоя в массив, переданный нам в качестве параметра:
void NeuralNet::getResult(uint16_t size, double* data) {
for (uint16_t r = 0; r < size; r++) {
data[r] = neurons[r][1][numLayers - 1];
}
}
Уход в закат
На этом мы приостановимся, следующая часть будет посвящена одной единственной функции, позволяющей обучить сеть. Из-за сложности и обилия математики я решил вынести её в отдельную часть, там же мы и протестируем работу всей библиотеки в целом.
Опять же, жду ваши советы и замечания в комментах.
Спасибо за уделённое внимание к статье, до скорого!
P.S.: Как и обещал — ссылка на исходники: GitHub
