[Из песочницы] Два способа быстрого вычисления факториала
Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1×2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.
Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:
static BigInteger FactNaive (int n) { BigInteger r = 1; for (int i = 2; i <= n; ++i) r *= i; return r; } На моей машине эта реализация работает примерно 1,7 секунд для N=50000.Далее я покажу два алгоритма, которые работают более чем в два раза быстрее наивной реализации.Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.
Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P (L, R). Разделим интервал от L до R пополам и посчитаем P (L, R) как P (L, M) * P (M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P (L, M) и P (M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P (L, R) = L, если L и R равны, и P (L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P (2, N).
Посмотрим, как будет работать наш алгоритм для N=10, найдем P (2, 10):
P (2, 10)P (2, 6) * P (7, 10)(P (2, 4) * P (5, 6)) * (P (7, 8) * P (9, 10))((P (2, 3) * P (4)) * P (5, 6)) * (P (7, 8) * P (9, 10))(((2×3) * (4)) * (5×6)) * ((7×8) * (9×10))((6×4) * 30) * (56×90)(24×30) * (5 040)720×5 0403 628 800
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне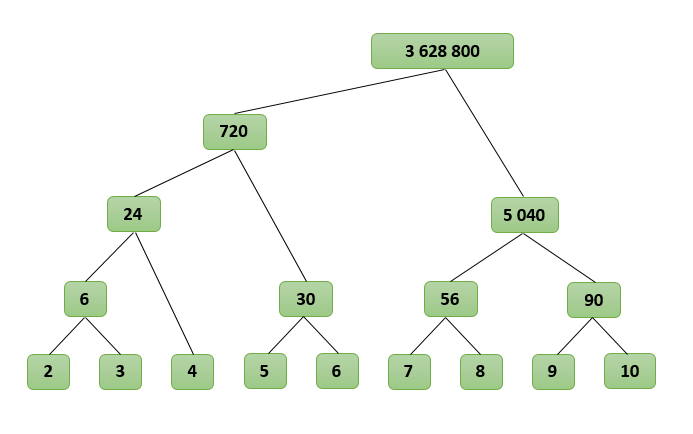
Реализуем описанный алгоритм:
static BigInteger ProdTree (int l, int r) { if (l > r) return 1; if (l == r) return l; if (r — l == 1) return (BigInteger)l * r; int m = (l + r) / 2; return ProdTree (l, m) * ProdTree (m + 1, r); } static BigInteger FactTree (int n) { if (n < 0) return 0; if (n == 0) return 1; if (n == 1 || n == 2) return n; return ProdTree(2, n); } Для N=50000 факториал вычисляется за 0,8 секунд, что вдвое быстрее, чем в наивной реализации.Второй способ быстрого вычисления использует разложение факториала на простые множители. Очевидно, что в разложении N! участвуют только простые множители от 2 до N. Попробуем посчитать, сколько раз простой множитель K содержится в N!, то есть узнаем степень множителя K в разложении. Каждый K-ый член произведения 1 * 2 * 3 *… * N увеличивает показатель на единицу, то есть показатель степени будет равен N / K. Но каждый K2-ый член увеличивает степень еще на единицу, то есть показатель становится N / K + N / K2. Аналогично для K3, K4 и так далее. В итоге получим, что показатель степени при простом множителе K будет равен N / K + N / K2 + N / K3 + N / K4 +…
Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (22), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (23), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (24) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.
Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:
10! = 28×34 * 52×71 = 3 628 800
Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:
static BigInteger FactFactor (int n)
{
if (n < 0)
return 0;
if (n == 0)
return 1;
if (n == 1 || n == 2)
return n;
bool[] u = new bool[n + 1]; // маркеры для решета Эратосфена
List
