[Из песочницы] Divide&Conquer над алгоритмом Штрассена

Привет друзья! Будучи студентами одного небезызвестного образовательного проекта, мы с bo_0m, после вводной лекции по курсу Углубленное программирование на Java, получили свое первое домашнее задание. Необходимо было реализовать программу, которая бы перемножала матрицы. И всё бы ничего, да так совпало, что на следующей неделе должна была состояться конференция Joker, и наш преподаватель решил отменить по такому случаю занятие, подарив нам несколько часов свободного пятничного вечера. Не пропадать же времени зря! Раз никто не торопит, то можно подойти к делу творчески.
Welcome, under the hood ↓
Наверно каждому студенту технического вуза приходилось перемножать матрицы. Алгоритм был всегда один, а именно, простенький кубический метод перемножения. Да и как бы это ни звучало, но данный способ не так-то уж и плох (для размерностей матриц меньше 100).
Все мы с этого начинали:
for (int i = 0; i < A.rows(); i++) {
for (int j = 0; j < A.columns(); j++) {
for (int k = 0; k < B.columns(); k++) {
C[i][j] += A[i][k] * B[k][j];
}
}
}
Забегая вперед, скажу, что мы будем использовать модифицированный вариант с применением транспонирования. Про такую модификацию хорошо написано здесь, да и не только про неё.
Окей, поехали дальше!
Алгоритм ШтрассенаВозможно, не все знают, но автор алгоритма Фолькер Штрассен не только жив, но и активно преподает, так же являясь почетным профессором кафедры математики и статистики Констанцского университета. Обязательно почитайте про этого человека хотя бы на вики.
Немножко теории из Википедии:
Пусть A и B — две (n*n)-матрицы, причём n — степень числа 2. Тогда можно разбить каждую матрицу A и B на четыре ((n/2)*(n/2))-матрицы и через них выразить произведение матриц A и B:
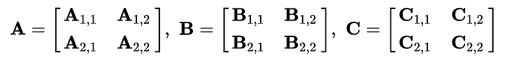
Определим новые элементы:
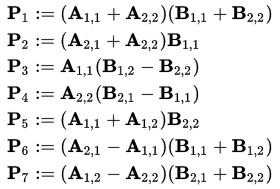
Таким образом, нам нужно всего 7 умножений на каждом этапе рекурсии. Элементы матрицы C выражаются из Pk по формулам:
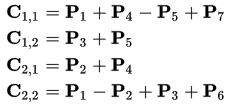
Рекурсивный процесс продолжается n раз, до тех пор пока размер матриц Ci, j не станет достаточно малым, далее используют обычный метод умножения матриц. Это делают из-за того, что алгоритм Штрассена теряет эффективность по сравнению с обычным на малых матрицах в силу большего числа сложений.
let’s go to practice!
Для реализации алгоритма Штрассена нам понадобятся дополнительные функции. Как было сказано выше, алгоритм работает только с квадратными матрицами, размерность которых равна степени 2, поэтому приведем исходные матрицы к такому виду.
Для этого была реализована функция, которая определяет новую размерность:
private static int log2(int x) {
int result = 1;
while ((x >>= 1) != 0) result++;
return result;
}
//******************************************************************************************
private static int getNewDimension(int[][] a, int[][] b) {
return 1 << log2(Collections.max(Arrays.asList(a.length, a[0].length, b[0].length)));
// Л - Лаконично
}
И функция, которая расширяет матрицу до нужного размера:
private static int[][] addition2SquareMatrix(int[][] a, int n) {
int[][] result = new int[n][n];
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < a[i].length; j++) {
result[i][j] = a[i][j];
}
}
return result;
}
Теперь исходные матрицы удовлетворяют требованиям для реализации алгоритма Штрассена. Также нам понадобится функция, которая позволит разбить матрицу размером n*n на четыре матрицы (n/2)*(n/2) и обратная для восстановления матрицы:
private static void splitMatrix(int[][] a, int[][] a11, int[][] a12, int[][] a21, int[][] a22) {
int n = a.length >> 1;
for (int i = 0; i < n; i++) {
System.arraycopy(a[i], 0, a11[i], 0, n);
System.arraycopy(a[i], n, a12[i], 0, n);
System.arraycopy(a[i + n], 0, a21[i], 0, n);
System.arraycopy(a[i + n], n, a22[i], 0, n);
}
}
//******************************************************************************************
private static int[][] collectMatrix(int[][] a11, int[][] a12, int[][] a21, int[][] a22) {
int n = a11.length;
int[][] a = new int[n << 1][n << 1];
for (int i = 0; i < n; i++) {
System.arraycopy(a11[i], 0, a[i], 0, n);
System.arraycopy(a12[i], 0, a[i], n, n);
System.arraycopy(a22[i], 0, a[i + n], n, n);
}
return a;
}
Вот мы и добрались до самого интересного, основная функция перемножения матриц алгоритмом Штрассена выглядит следующим образом:
private static int[][] multiStrassen(int[][] a, int[][] b, int n) {
if (n <= 64) {
return multiply(a, b);
}
n = n >> 1;
int[][] a11 = new int[n][n];
int[][] a12 = new int[n][n];
int[][] a21 = new int[n][n];
int[][] a22 = new int[n][n];
int[][] b11 = new int[n][n];
int[][] b12 = new int[n][n];
int[][] b21 = new int[n][n];
int[][] b22 = new int[n][n];
splitMatrix(a, a11, a12, a21, a22);
splitMatrix(b, b11, b12, b21, b22);
int[][] p1 = multiStrassen(summation(a11, a22), summation(b11, b22), n);
int[][] p2 = multiStrassen(summation(a21, a22), b11, n);
int[][] p3 = multiStrassen(a11, subtraction(b12, b22), n);
int[][] p4 = multiStrassen(a22, subtraction(b21, b11), n);
int[][] p5 = multiStrassen(summation(a11, a12), b22, n);
int[][] p6 = multiStrassen(subtraction(a21, a11), summation(b11, b12), n);
int[][] p7 = multiStrassen(subtraction(a12, a22), summation(b21, b22), n);
int[][] c11 = summation(summation(p1, p4), subtraction(p7, p5));
int[][] c12 = summation(p3, p5);
int[][] c21 = summation(p2, p4);
int[][] c22 = summation(subtraction(p1, p2), summation(p3, p6));
return collectMatrix(c11, c12, c21, c22);
}
На этом можно было бы и закончить. Реализованный алгоритм работает домашка выполнена, но пытливые умы жаждут взрослый perfomance. Да пребудет с нами Java 7. Пора распараллелить
Java 7 предоставляет прекрасный API для распараллеливания рекурсивных задач. С её выходом появилось одно из дополнений к пакетам java.util.concurrent — реализация парадигмы Divide and Conquer — Fork-Join. Идея заключается в следующем: рекурсивно разбиваем задачу на подзадачи, решаем, а потом объединяем результаты. Более подробно с данной технологией можно ознакомиться в документации.
Посмотрим как легко и эффективно можно применить эту парадигму к нашему алгоритму Штрассена.
private static class myRecursiveTask extends RecursiveTask {
private static final long serialVersionUID = -433764214304695286L;
int n;
int[][] a;
int[][] b;
public myRecursiveTask(int[][] a, int[][] b, int n) {
this.a = a;
this.b = b;
this.n = n;
}
@Override
protected int[][] compute() {
if (n <= 64) {
return multiply(a, b);
}
n = n >> 1;
int[][] a11 = new int[n][n];
int[][] a12 = new int[n][n];
int[][] a21 = new int[n][n];
int[][] a22 = new int[n][n];
int[][] b11 = new int[n][n];
int[][] b12 = new int[n][n];
int[][] b21 = new int[n][n];
int[][] b22 = new int[n][n];
splitMatrix(a, a11, a12, a21, a22);
splitMatrix(b, b11, b12, b21, b22);
myRecursiveTask task_p1 = new myRecursiveTask(summation(a11,a22),summation(b11,b22),n);
myRecursiveTask task_p2 = new myRecursiveTask(summation(a21,a22),b11,n);
myRecursiveTask task_p3 = new myRecursiveTask(a11,subtraction(b12,b22),n);
myRecursiveTask task_p4 = new myRecursiveTask(a22,subtraction(b21,b11),n);
myRecursiveTask task_p5 = new myRecursiveTask(summation(a11,a12),b22,n);
myRecursiveTask task_p6 = new myRecursiveTask(subtraction(a21,a11),summation(b11,b12),n);
myRecursiveTask task_p7 = new myRecursiveTask(subtraction(a12,a22),summation(b21,b22),n);
task_p1.fork();
task_p2.fork();
task_p3.fork();
task_p4.fork();
task_p5.fork();
task_p6.fork();
task_p7.fork();
int[][] p1 = task_p1.join();
int[][] p2 = task_p2.join();
int[][] p3 = task_p3.join();
int[][] p4 = task_p4.join();
int[][] p5 = task_p5.join();
int[][] p6 = task_p6.join();
int[][] p7 = task_p7.join();
int[][] c11 = summation(summation(p1, p4), subtraction(p7, p5));
int[][] c12 = summation(p3, p5);
int[][] c21 = summation(p2, p4);
int[][] c22 = summation(subtraction(p1, p2), summation(p3, p6));
return collectMatrix(c11, c12, c21, c22);
}
}
Кульминация
Вам, наверно, уже не терпится посмотреть на сравнение производительности работы алгоритмов на реальном железе. Сразу оговорим, что тестирование будем проводить на квадратных матрицах. Итак, мы имеем:
- Традиционный (Кубический) метод умножения матриц
- Традиционный с применением транспонирования
- Алгоритм Штрассена
- Распараллеленный алгоритм Штрассена
Размерность матриц будем задавать в интервале [100…4000] и с шагом в 100.
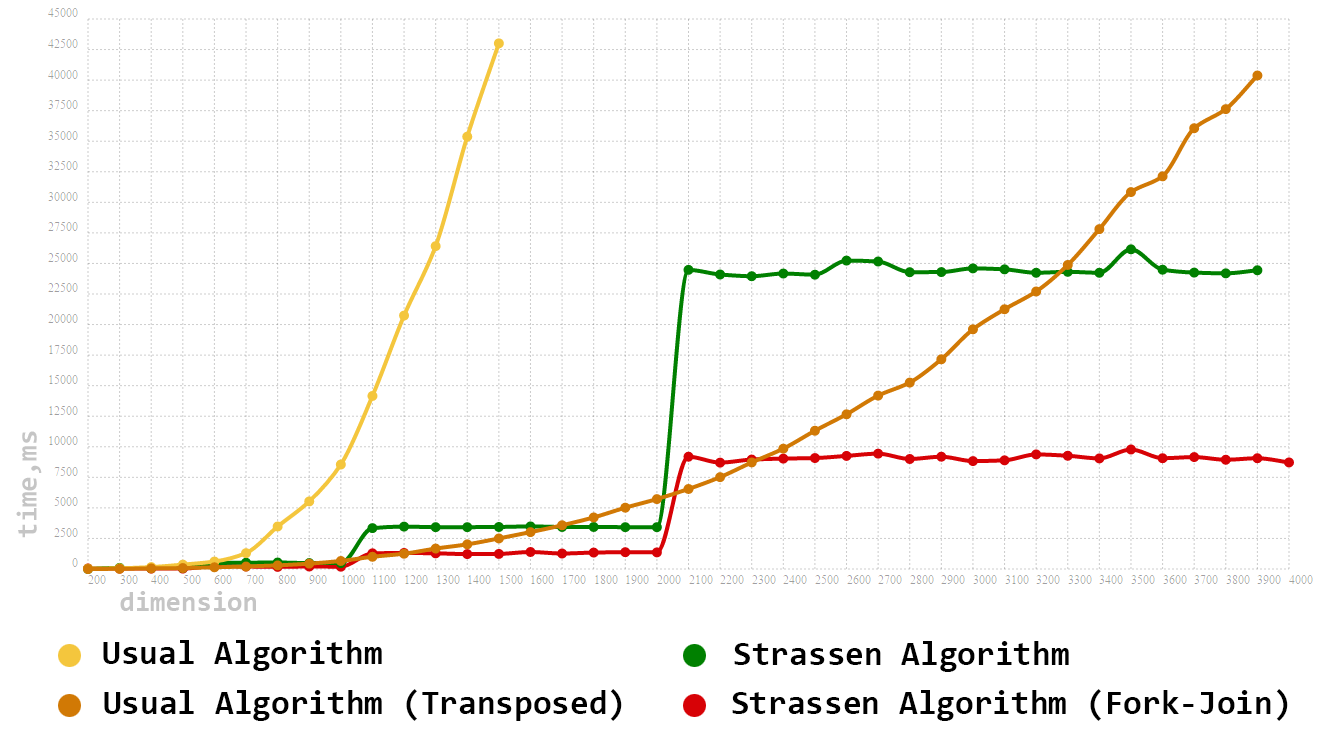
Как и ожидалось, наш первый алгоритм сразу выпал из тройки лидеров. Но вот с его модернизированным братом (вариант с транспонированием) не все так просто. Даже на довольно больших размерностях данный алгоритм не только не уступает, но и зачастую превосходит однопоточный алгоритм Штрассена. Особенности чтения многомерных массивов в Java дают о себе знать! И всё же, имея в рукаве козырь в виде Fork-Join Framework’а, нам удалось получить весомый прирост производительности. Распараллеливание алгоритма Штрассена позволило сократить время перемножения почти в 3 раза, а также возглавить наш итоговый тотал.
» Исходный код размещен здесь.
Будем рады отзывам и замечаниям к нашей работе. Спасибо за внимание!
