[Из песочницы] Диаграмма Вороного и её применения05.09.2016 19:03

Доброго всем времени суток, уважаемые посетители сайта Хабрахабр. В данной статье я бы хотел рассказать вам о том, что такое диаграмма Вороного (изображена на картинке ниже), о различных алгоритмах её построения (за $gif.latex?O(n^4)$ , $gif.latex?O(n^2*log(n))$ — пересечение полуплоскостей, $gif.latex?O(n*log(n))$ — алгоритм Форчуна) и некоторых тонкостях реализации (на языке C++).

Также будет рассмотрено много интересных применений диаграммы и несколько любопытных фактов о ней. Будет интересно!

План статьи:

— Необходимые понятия и определения
— Алгоритмы построения
— Применения
— Интересные факты
— Список литературы

Стоит отметить, что в данной статье будут рассматриваться только алгоритмы построения диаграммы Вороного на плоскости. Попутно будут рассмотрены некоторые другие алгоритмы, необходимые для построения диаграммы — алгоритм определения точки пересечения двух отрезков, алгоритм О`Рурка пересечения двух выпуклых многоугольников, алгоритм построения «береговой линии».

Необходимые понятия и определения

Сразу скажу, что всё, что будет дальше происходить, находится на плоскости.

Что ж, перед тем, как начать разбираться, что это такое — диаграмма Вороного, напомню некоторые понятия нужных нам геометрических объектов (предполагается, однако, что вы уже знакомы с определениями точки, прямой, луча, отрезка, многоугольника, вершины и ребра многоугольника, вектора и интуитивного понятия разбиения плоскости):

Простой многоугольник — это многоугольник без самопересечений. Мы будем рассматривать только простые многоугольники.

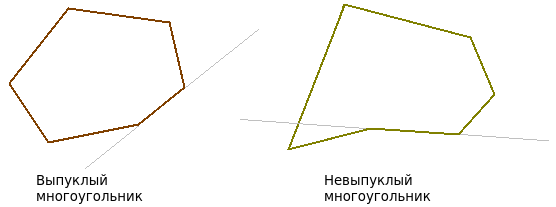
Невыпуклый многоугольник — это многоугольник, в котором найдутся такие две вершины, что через них проводится прямая, пересекающая данный многоугольник где-либо ещё, кроме ребра, соединяющего эти вершины (см. картинку),

Выпуклый многоугольник — это многоугольник, у которого продолжения сторон не пересекают других его сторон (см. картинку). С другими вариантами определений можно ознакомиться на википедии.

Именно из выпуклых многоугольников и будет состоять диаграмма. Почему именно из выпуклых? Потому что они являются ничем иным, как пересечением полуплоскостей (как мы увидим чуть позже), которые являются выпуклыми фигурами, а вот почему пересечение выпуклых фигур — выпуклая фигура, предложу вам узнать самим (доказательство есть, например, в книге [2]).

Раз уж я начал говорить про полуплоскости, то можно плавно перейти и к самой диаграмме — она состоит из так называемых локусов — областей, в которых присутствуют все точки, которые находятся ближе к данной точке, чем ко всем остальным. В диаграмме Вороного локусы являются выпуклыми многоугольниками.

Как строить локус? По определению он будет строиться так: пусть дано множество из n точек, для которого мы строим диаграмму. Возьмём конкретную точку p, для которой строим локус, и ещё одну точку из данного нам множества — q (не равную p). Проведём отрезок, соединяющий эти две точки, и проведём прямую, которая будет являться серединным перпендикуляром данного отрезка. Эта прямая делит плоскость на две полуплоскости — в одной лежит точка p, в другой лежит точка q. В данном случае локусами этих двух точек являются полученные полуплоскости. То есть для того, чтобы построить локус точки p, нужно получить пересечение всех таких полуплоскостей (то есть на месте q побывают все точки данного множества, кроме p).

Точку, для которой строится локус, называют сайтом (site). На следующей картинке локусы помечены разными цветами.

Алгоритмы построения диаграммы как раз и есть не что иное, как алгоритмы построения этих самых локусов для всех точек из заданного набора. Локусы в данной задаче также называют многоугольниками Вороного или ячейками Вороного.

Наконец, сформулируем определение диаграммы Вороного n точек на плоскости (n — натуральное) — это разбиение плоскости, состоящее из n локусов (для каждой точки по локусу). Опять же, другой вариант определения можно найти на википедии.

Кстати, вот сайт с интерактивным цветным визуализатором диаграммы Вороного, можно самому нажимать на область и залипать видеть, как строится диаграмма.

Если интересно, как появилась диаграмма и почему она носит фамилию Вороного, то вам стоит взглянуть под спойлер ниже.

Исторические факты

Немного истории

(материал взят с этого сайта)
Вообще, первое использование этой диаграммы встречается в труде Рене Декарта (1596–1650) «Начала философии» (1644). Декарт предложил деление Вселенной на зоны гравитационного влияния звезд.

28910aff9aa43df960a498f4803ddc7b_Descart

Только спустя два века, известный немецкий математик Иоганн Петер Густав Лежён-Дирихле (1805 — 1859) ввел диаграммы для двух- и трехмерного случаев. Поэтому их иногда называют диаграммами Дирихле.

Ну, а уже в 1908 году русский математик Георгий Феодосьевич Вороной (16(28) апреля 1868 — 7(20) ноября 1908) описал эту диаграмму для пространств бОльших размерностей, с тех пор диаграмма носит его фамилию. Вот его краткая биография (взято из википедии):

Георгий Феодосьевич Вороной родился в деревне Журавка Полтавской губернии (ныне Черниговская область). С 1889 года обучался в Санкт-Петербургском университете у Андрея Маркова. В 1894 году защитил магистерскую диссертацию «О целых числах, зависящих от корня уравнения третьей степени». В том же году был избран профессором Варшавского университета, где изучал цепные дроби. У Вороного обучался Вацлав Серпинский. В 1897 году Вороной защитил докторскую диссертацию «Об одном обобщении алгоритма непрерывных дробей», удостоенную премии имени Буняковского.

Алгоритмы построения

Научимся строить диаграмму Вороного. Мы рассмотрим 4 алгоритма, 2 из которых подробно (1 с реализацией, полной реализации алгоритма Форчуна будет посвящена отдельная статья), ещё 2 кратко (и без реализации):

Алгоритм построения диаграммы Вороного «в лоб». Сложность: $gif.latex?O(n^4)$ ;
Алгоритм построения диаграммы Вороного путём пересечения полуплоскостей. Сложность: $gif.latex?O(n^2*log(n))$ ;
Алгоритм Форчуна построения диаграммы Вороного на плоскости. Сложность: $gif.latex?O(n*log(n))$ ;
Рекурсивный алгоритм построения диаграммы Вороного. Сложность: $gif.latex?O(n*log(n))$ .

После описания некоторых алгоритмов будет приведена его реализация на языке C++. Для реализации использовалась написанная нами библиотека SplashGeom © — ссылка на github, в которой есть всё необходимое для реализации многих алгоритмов вычислительной геометрии на плоскости и некоторых в пространстве. Прошу не судить строго данную библиотеку, она ещё находится в стадии активной разработки и улучшения, однако все замечания будут услышаны.

Если же вам интересны другие реализации, то вот ещё некоторые:

boost.polygon
Сайт Стива Форчуна
aewllin/openvoronoi
Реализация на java
Реализация на JavaScript (там ещё и визуализатор есть)

Теперь перейдём к непосредственному рассмотрению алгоритмов:

Алгоритм построения диаграммы Вороного «в лоб» за $gif.latex?O(n^4)$

Здесь идея в том, чтобы пересекать не полуплоскости, а именно серединные перпендикуляры отрезков (потому что это проще, согласитесь), соединяющих данную точку со всеми другими точками. То есть мы, следуя определению ячейки Вороного, будем строить локус для точки p так:

Получаем n-1 прямую (серединные перпендикуляры), так как мы провели серединные перпендикуляры всех отрезков, соединяющих данную точку p с остальными;
Пересекаем попарно все прямые, получаем $gif.latex?O(n^2)$ точек пересечения (потому что каждая прямая может пересечь все другие, в «худшем случае»);
Проверяем все эти $gif.latex?O(n^2)$ точек на принадлежность каждой из n-1 полуплоскостей, то есть получаем уже асимптотику $gif.latex?O(n^3)$ . Соответственно те точки, которые принадлежат всем полуплоскостям, и будут вершинами ячейки Вороного точки p;
Проделываем первые три шага для всех n точек, получаем итоговую асимптотику $gif.latex?O(n^4)$ .

С алгоритмом также можно ознакомиться на e-maxx.ru.

При желании Вы самостоятельно можете реализовать этот алгоритм с помощью SplashGeom ©. В данной статье его реализация не приводится, потому как данный алгоритм на практике сильно уступает хотя бы следующему…

Алгоритм построения диаграммы Вороного путём пересечения полуплоскостей за $gif.latex?O(n^2*log(n))$

Этот алгоритм уже можно использовать на практике, так как он не имеет столь большой вычислительной сложности. Для него нам потребуется: уметь пересекать отрезки и прямые, уметь пересекать выпуклые многоугольники, уметь пересекать полуплоскости, уметь объединять полученные локусы в диаграмму.

Алгоритм

Получаем n-1 прямую для текущего сайта (как в предыдущем алгоритме — серединные перпендикуляры). Это будут «образующие» полуплоскостей;
Теперь мы имеем n-1 полуплоскость. Каждая из этих полуплоскостей задаётся какой-либо прямой из пред. пункта и ориентацией, то есть с какой стороны от прямой она расположена. Ориентацию можно определить по текущему сайту, для которого строим локус — он лежит в искомой полуплоскости, а значит и его локус должен лежать в ней;
Пересекаем все полуплоскости — мы сможем делать это за $gif.latex?O(n*log(n))$ — получаем локус для текущего сайта;
Проделываем первые три шага для всех n точек, получаем итоговую асимптотику $gif.latex?n$ * $gif.latex?O(n*log(n))$ = $gif.latex?O(n^2*log(n))$ .

Реализация

Основная загвоздка здесь, я считаю, реализовать нормальное пересечение выпуклых многоугольников, потому как там есть неприятные вырожденные случаи (совпадение вершин и/или сторон многоугольников; в случае пересечения многоугольника с самим собой надо неплохо подумать, чтобы адаптировать алгоритм О`Рурка для корректной работы в этом случае).

Сразу скажу, что мы ограничиваем всю область действий ограничивающим прямоугольником — полуплоскости будут отсекать от него части, которые мы и пересечём друг с другом. Это решает проблему бесконечных ячеек в диаграмме.

Пересечение прямых и отрезков
Причём нам нужны именно точки пересечения, а не просто определение его наличия. В SplashGeom © это есть — вот, к примеру, реализация пересечения прямых и отрезков:

Посмотреть код

// пересечение прямых
// kInfPoint - прямые параллельны, kNegInfPoint - прямые совпадают
Point2D Line2D::GetIntersection(const Line2D& second_line) const
{
	double cross_prod_norms = Vector2D(this->A, this->B).OrientedCCW(Vector2D(second_line.A, second_line.B));
	Point2D intersect_point;
	if (fabs(cross_prod_norms) <= EPS) /* A1 / A2 == B1 / B2 */ {
		if (fabs(this->B * second_line.C - second_line.B * this->C) <= EPS) /* .. == C1 / C2 */ {
			intersect_point = kNegInfPoint2D;
		} else {
			intersect_point = kInfPoint2D;
		}
	} else {
		double res_x = (second_line.C * this->B - this->C * second_line.B) / cross_prod_norms;
		double res_y = (second_line.A * this->C - this->A * second_line.C) / cross_prod_norms;
		intersect_point = Point2D(res_x, res_y);
	}
	return intersect_point;
}

// пересечение отрезков
Point2D Segment2D::GetIntersection(const Segment2D& second_seg) const
{
	Line2D first_line(*this);
	Line2D second_line(second_seg);
	Point2D intersect_point = first_line.GetIntersection(second_line);
	if (intersect_point == kNegInfPoint2D) {
		if (this->Contains(second_seg.b)) {
			intersect_point = second_seg.b;
		} else if (this->Contains(second_seg.a)) {
			intersect_point = second_seg.a;
		} else if (second_seg.Contains(this->b)) {
			intersect_point = this->b;
		} else if (second_seg.Contains(this->a)) {
			intersect_point = this->a;
		} else {
			intersect_point = kInfPoint2D;
		}
	} else if (!(this->Contains(intersect_point) && second_seg.Contains(intersect_point))) {
			intersect_point = kInfPoint2D;
	}
	return intersect_point;
}

Пересечение выпуклых многоугольников
Теперь реализуем пересечение многоугольников. Можно, конечно, делать это за $gif.latex?O(nm)$ , где n и m — количество вершин первого и второго многоугольника соответственно — пересекать каждую сторону первого многоугольника с каждой стороной из второго, записывая точки пересечения, а также проверять точки на принадлежность другому многоугольнику, но мы, дабы достичь лучшей скорости, будем пересекать по алгоритму О`Рурка (оригинальное описание алгоритма — [3]).

Также с одним из вариантов его описания можно ознакомиться на algolist.ru. У нас же реализация основана на описании алгоритма в книге [1] (стр. 334), с некоторыми дополняющими идеями. Сразу отмечу, что данная реализация не учитывает случаи, когда у многоугольников есть общие стороны (как отмечено в книге [1], этот случай требует отдельного рассмотрения), однако случаи с общими вершинами работают корректно.

Под спойлером ниже можно увидеть общее описание алгоритма.

Хочу знать алгоритм О`Рурка!

Алгоритм (за дополнительными пояснениями обратитесь к выше указанным источникам):

Пока не пройдёт максимальное количество итераций (доказывается, что оно не больше 2*(n + m)), выполняем следующие инструкции:
а). Берём текущие рёбра первого и второго многоугольников;
б). Если они пересекаются — тогда рассматриваем точку из пересечения: может быть так, что мы только что её добавили в многоугольник пересечения, тогда просто игнорируем добавление, иначе — если она не является начальной точкой пересечения (то есть мы уже сделали круг), то добавляем в пересечение, иначе заканчиваем алгоритм — мы встретили точку пересечения, которая была в начале;
в). Далее (независимо от того, пересекаются текущие рёбра или нет) вызываем функцию Движение, которая отвечает за передвижение окна первого (или второго) многоугольника на одно ребро вперёд, а также за возможное добавление вершины в многоугольник пересечения. Основные действия происходят именно в Движении.
Если не было точек пересечения, определить, лежит ли один многоугольник внутри другого (проверка принадлежности точки выпуклому многоугольнику за O (log (количество вершин многоугольника)) — [1], стр. 59–60). Если лежит, то вернуть его, иначе вернуть пустое пересечение.

Функцию Движения можно реализовывать по-разному, у нас она возвращает номер (метку) многоугольника, ребро которого мы двигаем. Концептуально она внутри себя делает три вещи:
— определяет номер случая — текущее взаимное расположение ребра первого многоугольника и ребра второго многоугольника. Это основная идея алгоритма — просмотр случаев положения рёбер относительно друг друга. Все эти четыре положения хорошо описаны в [1], в нашей реализации положение определяется с помощью косого произведения векторов на плоскости;
— определяет, ребро какого многоугольника сейчас «внутри», то есть оно лежит «слева» от другого ребра, у нас это тоже проверяется косым произведением (лежит «слева», если конечная точка лежит «слева»);
— решает, записывать ли текущий конец одного из рёбер в многоугольник пересечения. Если это соответствует нужному случаю и ребро внутри, то нужно добавить, иначе нет.

Ну, а в SplashGeom © это выглядит так:

Код пересечения многоугольников

// для получения многоугольников, которые полуплоскости отсекают от ограничивающего прямоугольника
Convex2D Rectangle::GetIntersectionalConvex2D(const Point2D& cur_point, const Line2D& halfplane) const
{
	vector convex_points;
	Segment2D cur_side;
	Point2D intersection_point;
	for (int i = 0, sz = vertices_.size(); i < sz; ++i) {
		int j = (i + 1) % sz;
		cur_side = Segment2D(vertices_[i], vertices_[j]);
		intersection_point = halfplane.GetIntersection(cur_side);
		if (intersection_point != kInfPoint2D)
			convex_points.push_back(intersection_point);
		if (halfplane.Sign(cur_point) == halfplane.Sign(vertices_[i]))
			convex_points.push_back(vertices_[i]);
	}
	Convex2D result_polygon(MakeConvexHullJarvis(convex_points));
	return result_polygon;
}
// определяет номер случая взаимного расположения рёбер
NumOfCase EdgesCaseNum(const Segment2D& first_edge, const Segment2D& second_edge)
{
	bool first_looks_at_second = first_edge.LooksAt(second_edge);
	bool second_looks_at_first = second_edge.LooksAt(first_edge);
	if (first_looks_at_second && second_looks_at_first) {
		return NumOfCase::kBothLooks;
	} else if (first_looks_at_second) {
		return NumOfCase::kFirstLooksAtSecond;
	} else if (second_looks_at_first) {
		return NumOfCase::kSecondLooksAtFirst;
	} else {
		return NumOfCase::kBothNotLooks;
	}
}
// определяет, какое ребро сейчас "внутри"
WhichEdge WhichEdgeIsInside(const Segment2D& first_edge, const Segment2D& second_edge)
{
	double first_second_side = Vector2D(second_edge).OrientedCCW(Vector2D(second_edge.a, first_edge.b));
	double second_first_side = Vector2D(first_edge).OrientedCCW(Vector2D(first_edge.a, second_edge.b));
	if (first_second_side < 0) {
		return WhichEdge::kSecondEdge;
	} else if (second_first_side < 0) {
		return WhichEdge::kFirstEdge;
	} else {
		return WhichEdge::Unknown;
	}
}
// функция Движения
WhichEdge MoveOneOfEdges(const Segment2D& first_edge, const Segment2D& second_edge, Convex2D& result_polygon)
{
	WhichEdge now_inside = WhichEdgeIsInside(first_edge, second_edge);
	NumOfCase case_num = EdgesCaseNum(first_edge, second_edge);
	WhichEdge which_edge_is_moving;
	switch (case_num) {
		case NumOfCase::kBothLooks: {
			if (now_inside == WhichEdge::kFirstEdge) {
				which_edge_is_moving = WhichEdge::kSecondEdge;
			} else {
				which_edge_is_moving = WhichEdge::kFirstEdge;
			}
			break;
		}
		case NumOfCase::kFirstLooksAtSecond: {
			which_edge_is_moving = WhichEdge::kFirstEdge;
			break;
		}
		case NumOfCase::kSecondLooksAtFirst: {
			which_edge_is_moving = WhichEdge::kSecondEdge;
			break;
		}
		case NumOfCase::kBothNotLooks: {
			if (now_inside == WhichEdge::kFirstEdge) {
				which_edge_is_moving = WhichEdge::kSecondEdge;
			} else {
				which_edge_is_moving = WhichEdge::kFirstEdge;
			}
			break;
		}
	}
	if (result_polygon.Size() != 0 && (case_num == NumOfCase::kFirstLooksAtSecond || case_num == NumOfCase::kSecondLooksAtFirst)) {
		Point2D vertex_to_add;
		if (now_inside == WhichEdge::kFirstEdge) {
			vertex_to_add = first_edge.b;
		} else if (now_inside == WhichEdge::kSecondEdge) {
			vertex_to_add = second_edge.b;
		} else { 
			if (case_num == NumOfCase::kFirstLooksAtSecond)
				vertex_to_add = first_edge.b; // ?!
			else
				vertex_to_add = second_edge.b;
		}
		if (vertex_to_add != result_polygon.GetCurVertex())
			result_polygon.AddVertex(vertex_to_add);
	}
	return which_edge_is_moving;
}
// пересечение выпуклых многоугольников (ссылка не константная только потому, что во втором многоугольнике двигается окно)
Convex2D Convex2D::GetIntersectionalConvex(Convex2D& second_polygon)
{
	Convex2D result_polygon;
	size_t max_iter = 2 * (this->Size() + second_polygon.Size());
	Segment2D cur_fp_edge; // current first polygon edge
	Segment2D cur_sp_edge; // current second polygon edge
	Point2D intersection_point;
	bool no_intersection = true;
	WhichEdge moving_edge = WhichEdge::Unknown;
	for (size_t i = 0; i < max_iter; ++i) {
		cur_fp_edge = this->GetCurEdge();
		cur_sp_edge = second_polygon.GetCurEdge();
		intersection_point = cur_fp_edge.GetIntersection(cur_sp_edge);
		if (intersection_point != kInfPoint2D) {
			if (result_polygon.Size() == 0) {
				no_intersection = false;
				result_polygon.AddVertex(intersection_point);
			} else if (intersection_point != result_polygon.GetCurVertex()) {
				if (intersection_point == result_polygon.vertices_[0]) {
					break; // we already found the intersection polygon
				} else {
					result_polygon.AddVertex(intersection_point);
				}
			}
		}
		moving_edge = MoveOneOfEdges(cur_fp_edge, cur_sp_edge, result_polygon);
		if (moving_edge == WhichEdge::kFirstEdge) {
			this->MoveCurVertex();
		} else {
			second_polygon.MoveCurVertex();
		}
	}
	if (no_intersection == true) {
		if (second_polygon.Contains(this->GetCurVertex())) {
			result_polygon = *this;
		} else if (this->Contains(second_polygon.GetCurVertex())) {
			result_polygon = second_polygon;
		}
	}
	return result_polygon;
}

Надеюсь, данное описание и код будут вам полезны. Пересечение полуплоскостей
Итак, у нас есть всё необходимое для построения пересечения полуплоскостей. Что ж, сделаем это, да сделаем не просто, а по-умному — в силу ассоциативности операции пересечения полуплоскостей, мы можем пересекать их в любом порядке, а значит пересечём две плоскости, потом пересечём ещё две, а потом пересечём их пересечения, это ведь уже быстрее, чем пересекать все по-отдельности.

Так что тут целесообразно использовать рекурсию (сразу настроение испортилось) — её работа здесь вполне понятна, сами посмотрите:

Посмотреть код

Convex2D GetHalfPlanesIntersection(const Point2D& cur_point, const vector& halfplanes, const Rectangle& border_box)
{
	if (halfplanes.size() == 1) {
		Convex2D cur_convex(border_box.GetIntersectionalConvex2D(cur_point, halfplanes[0]));
		return cur_convex;
	} else {
		int middle = halfplanes.size() >> 1;
		vector first_half(halfplanes.begin(), halfplanes.begin() + middle);
		vector second_half(halfplanes.begin() + middle, halfplanes.end());
		Convex2D first_convex(GetHalfPlanesIntersection(cur_point, first_half, border_box));
		Convex2D second_convex(GetHalfPlanesIntersection(cur_point, second_half, border_box));
		return first_convex.GetIntersectionalConvex(second_convex);
	}
}

Добавление локуса в диаграмму
Теперь мы имеем многоугольник Вороного данной точки, пора добавить его в диаграмму. Проблем с этим здесь особо не возникает, потому как мы получаем области в произвольном порядке, и между собой они никак не связаны (в отличие от реализации в алгоритме Форчуна, где можно перейти на соседний локус по указателю на ребро):

Посмотреть код

// строим локус для текущего сайта
Voronoi2DLocus VoronoiDiagram2D::MakeVoronoi2DLocus(const Point2D& site, const vector& points, const Rectangle& border_box)
{
	Voronoi2DLocus cur_locus;
	vector halfplanes;
	for (auto cur_point : points) {
		if (cur_point != site) {
			Segment2D cur_seg(site, cur_point);
			Line2D cur_halfplane(cur_seg.GetCenter(), cur_seg.NormalVec());
			halfplanes.push_back(cur_halfplane);
		}
	}
	*cur_locus.region_ = GetHalfPlanesIntersection(site, halfplanes, border_box);
	cur_locus.site_ = site;
	return cur_locus;
}
// строим диаграмму Вороного
VoronoiDiagram2D VoronoiDiagram2D::MakeVoronoiDiagram2DHalfPlanes(const vector& points, const Rectangle& border_box)
{
	Voronoi2DLocus cur_locus;
	for (auto cur_point : points) {
		cur_locus = MakeVoronoi2DLocus(cur_point, points, border_box);
		this->diagram_.push_back(cur_locus);
	}
	return *this;
}

Так, мы научились строить диаграмму Вороного за $gif.latex?O(n^2*log(n))$ , она имеет вид вектора (списка) локусов. Недостаток данного решения — информации о соседях не получить (возможно, этот недостаток можно ликвидировать улучшенной реализацией).

Куда больше информации можно получить из РСДС (DCEL). Эта структура будет использована в алгоритме Форчуна.

Далее будет описан алгоритм Форчуна с использованием заметающей прямой и «береговой линии» (готовьте купальники и плавки — идём на пляж). По моему мнению, это самый приемлемый вариант, если вы хотите реализовать построение диаграммы Вороного и строить её со «скоростью» света $gif.latex?O(n*log(n))$ .

Алгоритм Форчуна построения диаграммы Вороного за $gif.latex?O(n*log(n))$

В 1987 году Стив Форчун (Steve Fortune) предложил алгоритм построения диаграммы за $gif.latex?O(n*log(n))$ . Конечно, он является не единственным алгоритмом построения с такой асимптотикой, но он достаточно понятен и не очень сложен в реализации (да и, к тому же, очень красив и математичен!), поэтому я выбрал именно его.

Материалы по алгоритму Форчуна можно найти тут, здесь, вот здесь и ещё вот здесь.

Кстати, рассмотрению данного алгоритма уже была посвящена статья на Хабрахабре.

Итак, основная идея алгоритма — это так называемая заметающая прямая (ЗП) (sweep line). Она применяется во многих алгоритмах вычислительной геометрии, потому что позволяет удобно моделировать движение прямой по некоторому множеству объектов (например, в алгоритме пересечения n отрезков тоже используется sweep line).

Перед тем, как начать говорить про то, как и что мы будем делать, давайте посмотрим, как движется sweep line (взято отсюда):

Красиво, не правда ли? В реализации всё примерно так же, только ЗП обычно движется сверху вниз, а не слева направо, и на самом деле всё не так плавно, а происходит от события к событию (см. ниже), то есть дискретно.

Суть алгоритма

Есть n сайтов (точек на плоскости). Есть заметающая прямая, которая двигается (например) «сверху вниз», то есть от сайта с наибольшей ординатой к сайту с меньшей (от события к событию, если быть точным). Сразу стоит отметить, что влияние на построение диаграммы оказывают только те сайты, которые находятся выше или на заметающей прямой.

Когда ЗП попадает на очередной сайт (происходит событие точки (point event)), создаётся новая парабола (arch), фокусом которой является данный сайт, а директрисой — заметающая прямая (про параболу на википедии). Эта парабола делит плоскость на две части — «внутренняя» область параболы соответствует точкам, которые сейчас ближе к сайту, а «внешняя» область — точкам, которые ближе к sweep line, ну, а точки, лежащие на параболе — равноудалены от сайта и ЗП. Парабола будет меняться в зависимости от положения ЗП к сайту — чем дальше ЗП уходит от сайта вниз, тем больше расширяется парабола, однако в самом начале она вообще является отрезком («направленным» вверх).

Далее парабола расширяется, у неё появляются две контрольные точки (break points) — точки её пересечения с остальными параболами («береговой линией»). В «береговой линии» мы храним дуги парабол от одной точки пересечения их друг с другом до другой, так и получается beach line. По сути, в этом алгоритме мы моделируем движение этой «береговой линии». потому как эти самые break point`ы движутся аккурат по рёбрам ячеек Вороного (ведь получается, что контрольные точки равноудалены от обоих сайтов, которым соответствуют эти параболы, да ещё и от ЗП).

И как раз-таки в тот момент, когда две контрольные точки — по одной из разных парабол — «встречаются», то есть как бы превращаются в одну, эта точка и становится вершиной ячейки Вороного (происходит событие круга (circle event)), причём в это время та дуга, которая находилась между этими двумя точками — «схлопывается» и удаляется из «береговой линии». Далее мы просто соединяем эту точку с предыдущей соответствующей ей и получаем ребро ячейки Вороного.

Алгоритм

Итак, при движении sweep line вниз мы встречаемся с двумя типами событий: Событие точки (point event)
Событие точки — это попадание ЗП на один из сайтов, поэтому мы создаём новую параболу, соответствующую данному сайту, а также добавляются две контрольные точки (break points) (на самом деле сначала — одна, а при расширении арки уже две) — точки пересечения этой параболы с береговой линией (то есть с фронтом уже существующих парабол). Стоит отметить, что в данном алгоритме парабола (а точнее её часть, принадлежащая «береговой лини» — арка) «вставляется в береговую линию» только в случае события точки, то есть новая арка может появиться только при обработке события точки.

Кстати, на следующих картинках видно, почему объединения таких «кусков парабол» называют «береговой линией».

Событие круга (circle event)
Событие круга — это возникновение новой вершины ячейки Вороного вместе с удалением одной арки, потому что возникновение новой вершины диаграммы здесь означает, что было три арки, левая, средняя и правая, средняя «схлопывается» вследствие сближения левой и правой точек арок и получается новая вершина диаграммы Вороного. Стоит отметить, что в данном алгоритме парабола (арка) удаляется из «береговой линии» только в случае события круга, то есть арка может удалиться только при обработке события круга.

Есть теорема, в которой говорится, что вершина диаграммы Вороного всегда лежит на пересечении ровно трёх рёбер диаграммы, и есть следствие из этой теоремы, которое гласит, что вершина диаграммы является центром окружности, проходящей через три сайта и расстояние от этой точки до заметающей прямой тоже равно радиусу этой окружности (это свойство точек, лежащих на «береговой линии»). Это — ключевой момент, потому что именно когда самая нижняя точка окружности, проходящей через три сайта, лежит ниже или на заметающей прямой, мы пушим в очередь событий событие круга с этой самой нижней точкой, потому что когда прямая на неё попадёт, мы получим вершину диаграммы Вороного.

Важно, что с любым событием (точки или круга) связана одна конкретная арка, и наоборот. Это пригодится при обработке событий. Также надо не забыть, что нужно вовремя добавлять рёбра в РСДС (DCEL) (пункт 1 в структурах, см. ниже), так что надо понимать связь арок с рёбрами.

Таким образом, движение прямой дискретно — прямая в любой момент времени либо на сайте, либо в нижней точке окружности, проходящей через три сайта, центр которой — новая вершина диаграммы Вороного. Прекрасно.

Общий алгоритм:

Создаём очередь (с приоритетом) событий, изначально инициализируя событиями точки — данным множеством сайтов (ведь каждому сайту соответствует событие точки);
Пока очередь не пуста:
а). Берём из неё событие;
б). Если это — событие точки, то обрабатываем событие точки;
в). Если это — событие круга, то обрабатываем событие круга;
Закончить все оставшиеся рёбра (поработать с border_box).

Реализация

Реализация алгоритма Форчуна будет рассмотрена подробно в отдельной статье, однако здесь приводятся некоторые наработки, которые могут помочь в его понимании.Необходимые структуры
Для реализации данного алгоритма нам понадобятся несколько структур (классов), а именно:

РСДС (DCEL) — список для хранения уже найденный рёбер диаграммы Вороного;
Приоритетная очередь с событиями;
Двоичное дерево (у нас это BeachSearchTree) — для хранения «береговой линии» — текущего положения парабол и точек. Стоит отметить, что это дерево является сбалансированным — у узла либо ровно два сына, либо ноль (является листом). Подробнее об этой структуре можно прочитать, например, в этой статье на Хабре (у нас она представлена немного по-другому).

Имея такие структуры данных, можем написать реализацию общего алгоритма:

Посмотреть код

VoronoiDiagram2D VoronoiDiagram2D::MakeVoronoiDiagram2DFortune(const vector& points, const Rectangle& border_box)
{
	priority_queue events_queue(points.begin(), points.end());
	shared_ptr cur_event;
	BeachSearchTree beach_line;
	DCEL edges;
	while (!events_queue.empty()) {
		cur_event = make_shared(events_queue.top());
		shared_ptr is_point_event(dynamic_cast(cur_event.get()));
		if (is_point_event) {
			events_queue.pop();
			beach_line.HandlePointEvent(*is_point_event, border_box, events_queue, edges);
		} else {
			shared_ptr is_circle_event(dynamic_cast(cur_event.get()));
			events_queue.pop();
			beach_line.HandleCircleEvent(*is_circle_event, border_box, events_queue, edges);
		}
	}
	edges.Finish(border_box);
	this->dcel_ = edges;
	return *this;
}

Вся логика и сложность в HandlePointEvent () и HandleCircleEvent (), им и будет посвящена отдельная статья, далее же приведу некоторые вспомогательные функции, которые потом помогут в реализации.Вспомогательные функции
Пересечение парабол (арок)
Нам нужно уметь получать пересечение двух парабол (арок) в зависимости от положения ЗП. Уравнение параболы с фокусом в точке x' и y' и директрисой, положение которой по оси y равно l, задаётся следующим уравнением (его можно вывести):

$gif.latex?y&space;=&space;\frac{1}{2({y}$

Кстати, дробь перед скобкой — это фокальный параметр данной параболы. Отсюда мы можем «вытащить» соответствующие коэффициенты уравнения параболы и решить систему из двух нелинейных уравнений простым способом — вычтем одно из другого, а потом подставим найденные корни в первое, получим две точки. Нас интересует та точка, которая ниже (то есть с меньшей ординатой), потому что высокая точка лежит за «береговой линией». Описанные действия отражаются в следующем коде:

Код пересечения парабол

pair Arch::GetIntersection(const Arch& second_arch, double line_pos) const
{
	pair intersect_points;
	double p1 = 2 * (line_pos - this->focus_->y);
	double p2 = 2 * (line_pos - second_arch.focus_->y); // is not 0.0, because line moved down
	if (fabs(p1) <= EPS) {
		intersect_points.first = this->GetIntersection(Ray2D(*this->focus_, Point2D(this->focus_->x, this->focus_->y + 1)));
		intersect_points.second = intersect_points.first;
	} else {
		// solving the equation
		double a1 = 1 / p1;
		double a2 = 1 / p2;
		double a = a2 - a1;
		double b1 = -this->focus_->x / p1;
		double b2 = -second_arch.focus_->x / p2;
		double b = b2 - b1;
		double c1 = pow(this->focus_->x, 2) + pow(this->focus_->y, 2) - pow(line_pos, 2) / p1;
		double c2 = pow(second_arch.focus_->x, 2) + pow(second_arch.focus_->y, 2) - pow(line_pos, 2) / p1;
		double c = c2 - c1;
		double D = pow(b, 2) - 4 * a * c;
		if (D < 0) {
			intersect_points = make_pair(kInfPoint2D, kInfPoint2D);
		} else if (fabs(D) <= EPS) {
			double x = -b / (2 * a);
			double y = a1 * pow(x, 2) + b1 * x + c1;
			intersect_points = make_pair(Point2D(x, y), Point2D(x, y));
		} else {
			double x1 = (-b - sqrt(D)) / (2 * a);
			double x2 = (-b + sqrt(D)) / (2 * a);
			double y1 = a1 * pow(x1, 2) + b1 * x1 + c1;
			double y2 = a1 * pow(x2, 2) + b1 * x2 + c1;
			intersect_points = make_pair(Point2D(x1, y1), Point2D(x2, y2));
		}
	}
	return intersect_points;
}

Построение окружности по трём точкам
При обработке события круга нам понадобится определять центр и самую нижнюю точку окружности, построенной по фокусам трёх арок (сайтам). Есть некоторые аналитические алгоритмы построения окружности по трём точкам (под построением мы понимаем получение её центра и радиуса), у нас в программе это сделано так (спасибо алголисту) — соединяем отрезками первые две точки и вторые две точки. Центр лежит на пересечении серединных перпендикуляров, радиус — расстояние от центра до любой из трёх точек. Быстро и красиво:

Посмотреть код построения окружности по трём точкам

Circle::Circle(const Point2D& p1, const Point2D& p2, const Point2D& p3)
{
	Segment2D first_segment(p1, p2);
	Segment2D second_segment(p2, p3);
	Line2D first_perpendicular(first_segment.GetCenter(), first_segment.NormalVec());
	Line2D second_perpendicular(second_segment.GetCenter(), second_segment.NormalVec());
	center_ = first_perpendicular.GetIntersection(second_perpendicular);
	little_haxis_ = big_haxis_ = center_.l2_distance(p1);
}

Обработка события точки
Событие точки — это когда мы вытащили из очереди PointEvent. Что в нём есть? В нём есть только сайт, с которым ассоциируется это событие.

Что мы делаем при его обработке? Мы добавляем новую арку в «береговую линию», настраивая в дереве все связи «как надо», и проверяем, не появилось ли событие круга в одном из трёх возможных случаев — нам нужно проверить все случаи, в которых может участвовать новый сайт.

Что мы делаем при добавлении арки? Мы ищем для неё место в нашем двоичном дереве «береговой линии» (по координате x), затем вставляем её.

Что мы делаем при вставке? Мы нашли указатель на арку, с которой новая имеет пересечение в двух точках (случай с попаданием точки пересечения ровно на одну из контрольных точек рассматривается отдельно — там пересечение будет с двумя параболами — слева и справа).

То есть мы берём эту арку, которая «разбивается», и вместо неё вставляем аж 5 узлов (был 1, стало 5, да) — arch1, bp1, arch2, bp2, arch3. Arch1 — это левый кусок арки, которую пересекает новая, то есть это кусок слева от левого break point`а, bp1 — левый break point (левое пересечение новой арки), arch2 — это новая арка собственной персоной, bp2 — правый break point (правое пересечение новой арки), arch3 — это правый кусок арки, которую пересекает новая.

Стоит отметить, что событие точки даёт начало новому ребру (или рёбрам, есть случаи) диаграммы Вороного.

Один из возможных вариантов добавления новой арки в «береговую линию» представлен в этой статье на Хабре, наш же вариант описан выше, и больше похож на тот, который предложен здесь.

Обработка события круга
Событие круга — это когда мы вытащили из очереди CircleEvent.

Что в нём есть? В нём есть точка — это самая нижняя точка некоторой окружности, которая проходит через три каких-то сайта, и арка, которую следует удалить. В дереве есть две её контрольные точки и она сама, контрольные точки в итоге превратятся в одну, а арку нужно аккуратно удалить из дерева, перестроив все «связи родителей-детей». По сути, обработка этого события заменя