[Из песочницы] Число Бейкона и Графы
Число Бейкона Немного история, Кевин Бейкон американский актёр сыгравший во множествах фильмам, в 1994 отметил что актёры, с которыми снимался он, работали со всеми голливудскими (и не только) актёрами. Общественность тут же отреагировала и создала игру «назвать имя актёра и связать его с Кевином Бейконом». Корпорация добра даже встроила игру в свой поисковик, например Число Бейкона для актёра Джона Траволты равно 2 (Джон снимался с Оливией Ньютон-Джон в фильме Бриолин, она же, в свою очередь, сыграла с Кевином Бейконом в фильме «У нее будет ребенок»).А теперь давайте поговорим о том как это игру можно представить и как можно вычислить число Бейкона при помощи графа.
Граф
В данном случае, я буду рассматривать направленный невзвешенный граф, где вершинами будут актеры и ребрами фильмы (данные можно взять с IMDb), в которых они снимались, под стартовой (нулевой) вершиной будет Кевин Бейкон. Число Бейкона в таком графе будет равно количеству hop`ов от стартовой вершины до искомой или для всех остальных. Для примера я выбрал такой вот граф: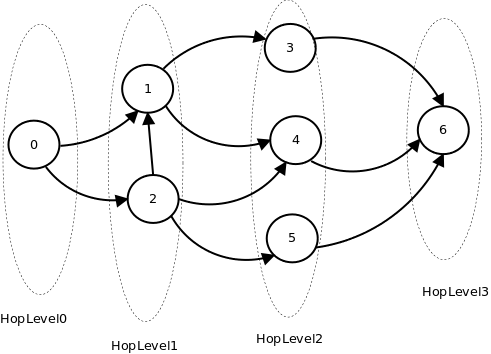 
Алгоритм который производит поиск называется «Поиск в ширину» (Breadth-first search) и делает необходимые нам вычисления за O (n+m) операций, где n — количество вершин, а m — количество рёбер, то есть, за линейное время, что весьма неплохо. Для реализации алгоритма нам понадобится обычная очередь (FIFO), куда мы будет помещать все встретившиеся нам вершины.И так первый шаг, взять стартовую вершину и поместить её в очередь. Далее у нас будет цикл условием выхода из которого будет проверка очереди на пустоту. В каждой итерации достаём вершину из очереди, берём всех потомков этой вершины, при этом помечая ребро как исследованное, и если вершина все ещё не исследована то помечаем её таковой и отправляем в очередь.
Как это выглядит на нашем примере: — помечаем вершину0 как стартовую и помещаем её в очередьДалее цикл пока очередь не пуста— достаём нулевую вершину, по рёбрам (0,1) и (0,2) берём потомков, т.к. эти вершины встречаются нам первый раз то помешаем их в очередь, отметив их исследованными и установив их HopLevel на единицы больше чем у родителя (в данном случае 1)— следующая вершина, при её обработки в очередь попадут вершины 3 и 4, при этом уровень для них установится равный 2— далее вершина2, в этом случаем потом 4 не попадёт в очередь т.к. он уже исследован выше, только 5 будет отравлена в очередь с уровнем равным 2— вершина 3, которая отправит в очередь потомка 6 с уровнем 3— остальные вершины будет просто изъяты из очереди.— на вершине6 очередь опустеет и цикл завершится
Небольшой код на Go: Код package main
import ( «container/heap» «fmt» )
type Node struct { HopLevel int Explored bool Edges []int index int //internal variable } type Graph []*Node type Queue []*Node
func (q Queue) Len () int { return len (q) } func (q Queue) Less (i, j int) bool { return q[i].index < q[j].index } func (q Queue) Swap(i, j int) { q[i], q[j] = q[j], q[i] }
func (q *Queue) Push (x interface{}) { *q = append (*q, x.(*Node)) } func (q *Queue) Pop () interface{} { old:= *q n:= len (old) x:= old[n — 1] *q = old[0: n-1] return x }
var ( operationsNumber int = 0; )
func main () { g:= createGraph () bfs (*g, 0) for index, node:= range *g { fmt.Printf (» node%d is on %d HopLevel \n», index, node.HopLevel) } fmt.Printf («Total number of operations is %d», operationsNumber) }
func bfs (g Graph, startIndex int) { queue:= &Queue{} heap.Init (queue) start:= g[startIndex] start.index = 0 start.HopLevel = 0; start.Explored = true; index:= 1; heap.Push (queue, start) for queue.Len () > 0 { node:= heap.Pop (queue).(*Node) for _, childNodeIndex:= range node.Edges { childNode:= g[childNodeIndex] if! childNode.Explored { childNode.Explored = true childNode.HopLevel = node.HopLevel+1 childNode.index = index index++ heap.Push (queue, childNode) } operationsNumber++ } operationsNumber++ } }
func createGraph () *Graph { node0:= &Node{ Edges: []int{1, 2}, } node1:= &Node{ Edges: []int{3, 4}, } node2:= &Node{ Edges: []int{1, 4, 5}} node3:= &Node{ Edges: []int{6}} node4:= &Node{ Edges: []int{6}} node5:= &Node{ Edges: []int{6}} node6:= &Node{ Edges: []int{}} return &Graph{node0, node1, node2, node3, node4, node5, node6} } В реализации я использовал пакет heap, который позволяет создать нужную нам очередь определив 5 методов, так же, в структуре Node появилась внутренняя переменная index, необходимая нам для очереди.
Результаты: node0 is on 0 HopLevel node1 is on 1 HopLevel node2 is on 1 HopLevel node3 is on 2 HopLevel node4 is on 2 HopLevel node5 is on 2 HopLevel node6 is on 3 HopLevel Total number of operations is 17 Граф который указан на рисунке выше состоит из 7 вершин и 10 рёбер, и как мы видим количество операций равно 17 и каждой вершины определён уровень насколько она далека от стартовой.
Примечания: — Вместо пакета heap можно было бы использовать chanel и это было бы более разумно— Так как граф направленный, я не стал отмечать ребра как исследованные.— Алгоритм можно использовать для конкретной вершины, тогда к условию выхода так же добавиться проверка не искомая ли вершина взята из очереди на обработку.— Кевин Бейкон не является самым оптимальным актёром для такой игры, есть кандидаты значительно лучше, максимальное число Бейкона равно 9.
