[Из песочницы] Частное решение общей задачи электростатики
Со школы мы помним решение задачи о распределении электрического заряда по бесконечной проводящей плоскости в присутствии точечного электрического заряда над плоскостью. Только некоторые вспомнят как аналитически решается задача о распределении электрического заряда по проводящей сфере, если точечный заряд покоится где-то в пространстве. Но, я уверен, никто не сможет решить аналогичную задачу о распределении заряда по бутылке Клейна. Если к такой системе добавить внешнее электростатическое поле и другие проводники, об аналитическом решении глупо будет даже мечтать.Сформулируем общую задачу электростатики следующим образом:
Дано: — форма и расположение в пространстве проводников— заряд проводников— внешнее электрическое поле (поле в отсутствие проводников, не зависящее от положения проводников)
Необходимо найти распределение заряда по поверхности проводников и скалярный потенциал электрического поля во всём пространстве.
Потенциал как функция трёх декартовых координат должен удовлетворять уравнению Пуассона во всём пространстве:
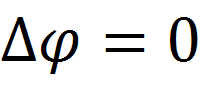
Из теоремы единственности следует, что, если мы найдём функцию, удовлетворяющую этому уравнению и граничным условиям, т.е. решение, это решение будет единственным.
Дабы избежать излишней сложности, рассмотрим решение задачи о распределении электрического заряда по проводящей поверхности в присутствии внешнего поля, не зависящего от положения и заряда проводящей поверхности.
Будем искать решение задачи численно методом конечных элементов.
Сразу предупрежу, что я не буду рассматривать теоретически вопрос сходимости моего метода, а ограничусь лишь некоторыми фактами из практики, свидетельствующими в пользу гипотезы о сходимости этого метода, хотя, возможно, и не к истинному решению.
Зададим поверхность параметрически:
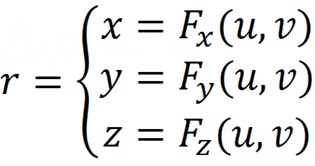
Выберем количество u и v — разбиений и покроем поверхность сетью u и v — линий. В узлах полученной сетки поместим электрические заряды, величину которых нам предстоит найти.Также выберем Nu*Nv точек в непосредственной близости от узлов. Решение будем искать исходя из условия, что потенциал электрического поля в этих точках одинаков. Сам потенциал будем рассчитывать как суперпозицию потенциалов, создаваемых точечными зарядами.
Составим матрицы:
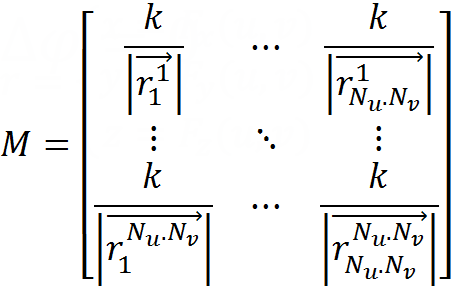— набросок матрицы линейной системы, которую будем решать. Нижние индексы говорят о положении зарядов, верхние — точек рассмотрения потенциала. Эти расстояния находятся из параметризации поверхности.
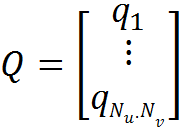— матрица-столбец неизвестных — величин зарядов.
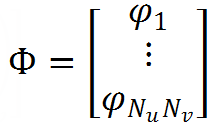— матрица-столбец потенциалов внешнего поля в точках рассмотрения потенциала.
Тогда получим систему Ф+MQ=A, где А — некая постоянная матрица-столбец, составленная из неизвестных нам потенциалов поверхности.
Чтобы исключить этот потенциал из системы, сначала перенесём матрицу Ф в правую часть равенства, а затем отнимем от Nu*Nv-1 первых уравнений системы последнее уравнение, которое заменим условием нормировки (сумма всех зарядов на поверхности равна полному заряду).
Тогда получим финальную линейную систему с матрицей системы:
И столбцом свободных членов:
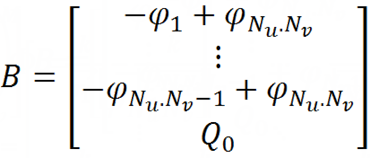
Чтобы покончить с этими картинками с чрезмерно большим шрифтом, приведу последнее выражение, определяющее результат всей работы — кусочно-постоянную функцию поверхности заряда на поверхности (имеется в виду, что при u и v, принадлежащими площадке приближения с одноименными индексами, функция принимает значение левой части выражения):
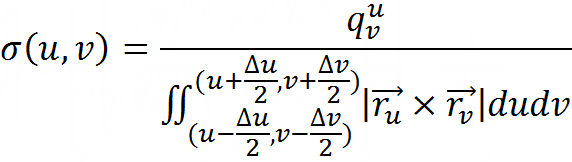
Будем решать систему и работать с результатом в системе Mathematica.
Частное решение общей задачи электростатики.nb
Посмотрим теперь на работу метода. Начнём с квадратной пластины, параметризованной тривиальным способом. Тогда параметры u и v — декартовы координаты точек пластины и элемент площади, что стоит под интегралом выше равен единице.
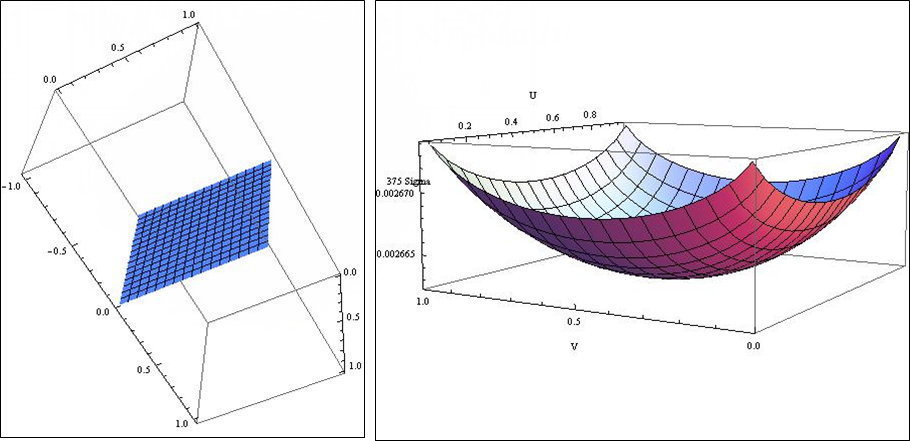
Мы получили логичное и ожидаемое решение.
Решением для сферы должна быть плоскость, но мы получаем что-то совсем нехорошее:
Я всё объясню. Дело в том, что выбор точек помещения зарядов и рассмотрения потенциалов зависит от параметризации. И на такой симметричной системе, как сфера, получаем несимметричный результат из-за того, что поверхностная плотность заряда является поверхностной в «декартовом смысле». Если бы мы вводили поверхностную плотность в сферической системе координат, всё было бы иначе.
Но не всё так плохо. При увеличении узлов эта фигурка сжимается (на автоматически построенным математикой графике этого, правда, не видно) и, предполагаю, стремится таки занять место плоскости.
Поверхности, для которых ведётся поиск решения, должны быть замкнутыми, иначе может возникнуть сингулярность на краях: при увеличении точности плотность заряда на краях стремится к бесконечности.
Также я решил решить задачу о распределении заряда по полуокружности («бусы») двумя способами для проверки работы метода.
Метод 1. Расположим на бусах одинаковые заряды. Заряды безынерционные. «Отпустим» их. Маленькими шажками они займут устойчивое положение. Такой наглядный метод зейделевского типа относительно угловой координаты зарядов:
Метод 2. Вышеописанной системе соответствует полуцилиндр в трёхмерном пространстве, для которого задачу решим нашим методом:
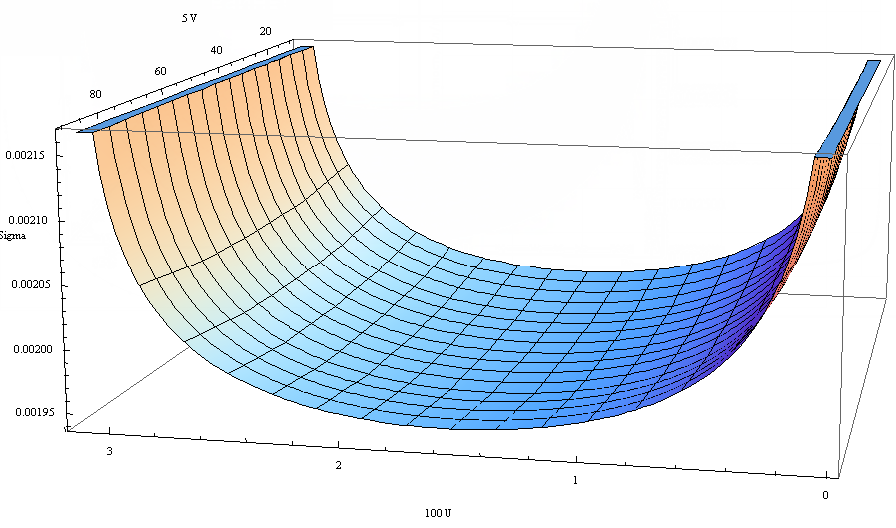
Внешне решения очень даже похожи. Q.E. D.
Интересно услышать ваше мнение по поводу вышеизложенного метода решения общей задачи электростатики.
