[Из песочницы] Алгоритм создания списка всех перестановок или размещений
Сразу оговорюсь, эта статья тематически похожа на опубликованную около года назад автором SemenovVV «Нерекурсивный алгоритм генерации перестановок», но подход тут, на мой взгляд, принципиально иной.
Я столкнулся с необходимостью составления списка всех перестановок из n элементов. Для n = 4 или даже 5, задача решается вручную в считанные минуты, но для 6! = 720 и выше исписывать страницы мне уже было лень — нужна была автоматизация. Я был уверен, что этот «велосипед» уже изобретён многократно и в различных вариациях, но было интересно разобраться самостоятельно — поэтому, намеренно не заглядывая в профильную литературу, я засел за создание алгоритма.
Первую же версию кода с рекурсией я отбросил как слишком тривиальную и ресурсоёмкую. Далее, сделав «финт ушами», разработал не очень эффективный алгоритм, перебирающий заведомо большее количество вариантов и отсеивающий лишь подходящие из них. Он работал, но мне хотелось чего-то элегантного — и, начав с чистого листа, я принялся искать закономерности в лексикографическом порядке перестановок для малых значений n. В итоге получился аккуратный код, который с минимальной «обвязкой» можно на Python представить строк в 10 (см. ниже). Более того, этот подход работает не только для перестановок, но и для размещений n элементов по m позициям (в случае когда, n≥m).
Если взглянуть на перечень всех перестановок для 4 по 4, то заметна определённая структура:
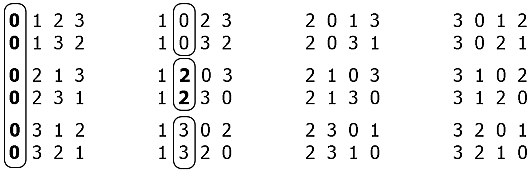
Весь массив перестановок (4! = 24) можно разбить на группы из (n-1)! = 3! — шести перестановок, а каждую группу в свою очередь разбить на (n-1–1)! = 2! –две комбинации и так далее. В рассмотренном случае, когда для n = 4, на этом — всё.
Итак, с точки зрения лексикографии этот набор перестановок можно представить себе как возрастающий ряд: так сказать, 0123 < 0132 < … < 3210. Мы наперёд знаем, сколько раз подряд будет повторяться один и тот же элемент в определённой позиции – это количество перестановок для массива порядком на единицу меньше, т.е. (a-1)! , где а — размерность текущего массива. Тогда признаком перехода к следующему значению будет новый результат целочисленного деления (»//») порядкового номера i комбинации на количество таких перестановок: i // (a-1)! . Также, чтобы определить, каким будет номер этого элемента в списке ещё не задействованных (дабы не перебирать его по кругу), используем остаток от деления (»%») полученной величины на длину этого списка. Т.о. имеем следующую конструкцию:
i // (a-1)! % r,
где r — размерность массива ещё не задействованных элементов.
Для наглядности рассмотрим конкретный случай. Из всех 24 перестановок i Є [0, 23] 4 элементов по 4 положениям, к примеру, 17-я будет представлять собой следующую последовательность:
[17 // (4–1)!] % r(0,1,2,3) = 2% 4 = 2
(т.е., если считать с 0, третий элемент списка, — »2»). Следующим элементом этой перестановки будет:
[17 // (3–1)!] % r(0,1,3) = 8% 3 = 2
(снова третий элемент — теперь это »3»)
Если продолжать в том же духе, в итоге получим массив »2 3 1 0». Следовательно, перебирая в цикле все значения i из количества перестановок [n! ] или размещений [n!/(n-m)! , где m — количество положений в массиве], мы получим исчерпывающий набор искомых сочетаний.
Собственно, сам код выглядит так:
import math
elm=4 # к-во элементов, n
cells=4 # к-во положений, m
res=[] # результирующий список
arrang = math.factorial(elm)/math.factorial(elm-cells) # расчёт к-ва сочетаний
for i in range(arrang):
res.append([])
source=range(elm) # массив ещё не задействованных элементов
for j in range(cells):
p=i//math.factorial(cells-1-j)%len(source)
res[len(res)-1].append(source[p])
source.pop(p)
