[] Бикватернионы
Если вы открыли данную статью, то наверняка уже слышали о кватернионах, и возможно даже используете их в своих разработках. Но пора подняться на уровень выше — к бикватернионам. Можно и еще выше — к седионам! Но не сейчас.
В данной статье даны основные понятия о бикватернионах и операции работы с ними. Для лучшего понимания работы с бикватернионами показан наглядный пример на Javascript с использованием Canvas.
Определение бикватерниона
Бикватернион — гиперкомплексное число, имеющее размерность 8. В англоязычных статьях и литературе они называются — «dual quaternion», в русскоязычной литературе встречается еще названия «октонион», «дуальный кватернион» или «комплексный кватернион».
Основное отличие от кватернионов заключается в том, что кватернион описывает ориентацию объекта в пространстве, а бикватернион еще и положение объекта в пространстве.
Бикватернион можно представить в виде двух кватернионов:
$$display$$\widetilde{\textbf{q}} = \begin{bmatrix} \textbf{q}_1 \\ \textbf{q}_2 \end{bmatrix},$$display$$
$inline$\textbf{q}_1$inline$ — действительная часть, определяет ориентацию объекта в пространстве;
$inline$\textbf{q}_2$inline$ — дуальная часть, определяет положение объекта в пространстве.
Бикватернион также называют еще комплексным кватернионом, в этом случае его представляют в виде кватерниона, каждый компонент которого представляет собой дуальное число (не путать с комплексным). Дуальное число $inline$A = a_1 + \epsilon a_2$inline$, где $inline$a_1$inline$ и $inline$a_2$inline$ — действительные числа, а $inline$\epsilon$inline$ — символ (комплексность) Клиффорда, обладающий свойством $inline$\epsilon^2 = 0$inline$. Не будем углубляться в математику, так как нас интересует больше прикладная часть, поэтому далее — бикватернион будем рассматривать как два кватерниона.
Геометрическая интерпретация бикватерниона
По аналогии с кватернионом, с помощью которого можно задать ориентацию объекта, бикватернионом можно задать еще и положение. Т.е. бикватернион задает сразу две величины — положение и ориентацию объекта в пространстве. Если их рассматривать в динамике, то бикватернион определяет две величины — линейную скорость перемещения и угловую скорость вращения объекта. На рисунке ниже показан геометрический смысл бикватерниона.
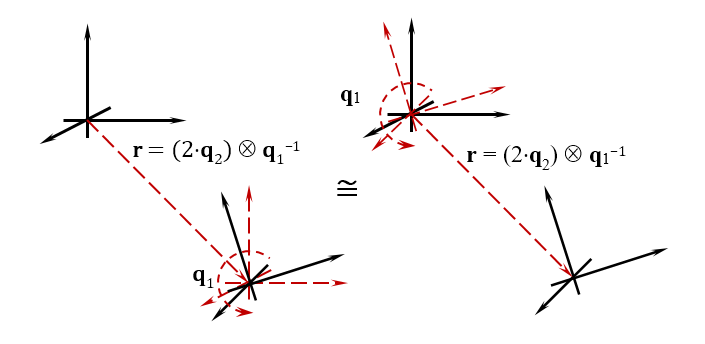
Разработчики игр знают, чтобы задать положение и ориентацию объекта в игровом пространстве применяются матрицы поворотов и матрицы перемещений, и, в зависимости от того, в какой последовательности вы их применяете, результат конечного положения объекта разный. Для тех, кто привык разделять движение на отдельные операции, для работы с бикватернионами примите за правило: сначала объект перемещаем, потом поворачиваем. Фактически, вы одним числом, пусть и сложным гиперкомплексным, описываете эти два движения.
Скалярные характеристики
Рассмотрим основные скалярные характеристики. Здесь надо обратить внимание на то, что они возвращают не обычные вещественные числа, а дуальные.
1. Норма бикватерниона
$$display$$\|\widetilde{\textbf{q}}\| = \|\textbf{q}_1\| + \epsilon (q_{1_0} q_{2_0} + \textbf{q}_1^T \textbf{q}_2)$$display$$
2. Модуль бикватерниона
$$display$$|\widetilde{\textbf{q}}| = |\textbf{q}_1| + \epsilon\frac{q_{1_0} q_{2_0} + \textbf{q}_1^T \textbf{q}_2}{|\textbf{q}_1|}$$display$$
Основные операции
Рассмотрим основные операции работы с бикватернионами. Как вы можете заметить, они очень похожи на аналогичные операции работы с кватернионами.
1. Бикватернионное сопряжение
$$display$$\widetilde{\textbf{q}}^* = \begin{bmatrix} \textbf{q}_1^* \\ \textbf{q}_2^* \end{bmatrix}$$display$$
2. Бикватернионное сложение и вычитание
$$display$$\widetilde{\textbf{q}} \pm \widetilde{\textbf{p}} = \begin{bmatrix} \textbf{q}_1 \pm \textbf{p}_1 \\ \textbf{q}_2 \pm \textbf{p}_2 \end{bmatrix}$$display$$
Сложение и вычитание бикватернионов коммутативно (слагаемые можно менять местами).
3. Умножение действительного числа на бикватернион
$$display$$a\widetilde{\textbf{q}} = \widetilde{\textbf{q}}a = \begin{bmatrix} a\textbf{q}_1 \\ a\textbf{q}_2 \end{bmatrix}$$display$$
4. Бикватернионное умножение
$$display$$\widetilde{\textbf{q}} \otimes \widetilde{\textbf{p}} = \begin{bmatrix} \textbf{q}_1 \otimes \textbf{p}_1 \\ \textbf{q}_1 \otimes \textbf{p}_2 + \textbf{q}_2 \otimes \textbf{p}_1 \end{bmatrix}$$display$$
Бикватернионное умножение некоммутативно (при изменении порядка сомножителей результат бикватернионного умножения разный).
Данная операция является одной из основных при работе с бикватернионами и несет в себе физический смысл, а именно, результатом бикватернионного умножения является операция сложения поворотов и линейных перемещений двух бикватернионов.
5. Обратный бикватернион
$$display$$\widetilde{\textbf{q}}^{-1} = \frac{\widetilde{\textbf{q}}^*}{\|\widetilde{\textbf{q}}\|}$$display$$
Определение бикватерниона через углы ориентации и вектор положения
Для начала определим системы координат, в которых будем рассматривать ориентацию и положение объекта в пространстве. Это необходимо сделать для задания действительной части бикватерниона (кватерниона ориентации), последовательность поворотов которого влияет на получаемый кватернион из углов ориентации. Здесь будем руководствоваться самолетными углами — рысканья $inline$\psi$inline$, тангажа $inline$\vartheta$inline$ и крена $inline$\gamma$inline$.
Определим базовую систему координат. Представьте, что вы стоите на поверхности Земли и смотрите в направлении Севера.
Точка Oo — начало системы координат, располагается в точке начала движения объекта.
Ось OoYg — направленна вертикально вверх, и противоположна к направлению вектора силы тяжести.
Ось OoXg — направлена в сторону Севера, по касательной местного меридиана.
Ось OoZg — дополняет систему до правой и направлена вправо, в сторону Востока.
Вторая система координат — связанная. Представьте, например, самолет или другой объект.
Точка O — начало системы координат, как правило, располагается в точке центра масс объекта.
Ось OY — направлена вертикально вверх, и перпендикулярна горизонтальной плоскости объекта.
Ось OX — направлена вперед, к передней точке объекта.
Ось OZ — дополняет систему до правой.
Положение объекта в пространстве задается радиус-вектором начала (точка O) связанной системы координат относительно неподвижной базовой системы координат. Ориентация связанной системы координат относительно базовой определяется тремя последовательными поворотами на:
угол рысканья $inline$\psi$inline$ — поворот вокруг оси OY,
угол тангажа $inline$\vartheta$inline$ — поворот вокруг оси OZ,
угол крена $inline$\gamma$inline$ — поворот вокруг оси OX.
Для первоначального определения бикватерниона необходимо задать действительную и дуальную части бикватерниона. Ориентация и положение объекта задается относительно некой базовой системы координат с помощью углов ориентации $inline$\psi, \vartheta, \gamma$inline$ и вектора положения центра масс $inline$r = (r_x, r_y, r_z)^T$inline$.
Действительную часть $inline$\textbf{q}_1$inline$ можно задать с помощью формулы:
$$display$$ \textbf{q}_1 = \begin{bmatrix} \cos\frac{\psi}{2} \cos\frac{\vartheta}{2} \cos\frac{\gamma}{2} & — & \sin\frac{\psi}{2} \sin\frac{\vartheta}{2} \sin\frac{\gamma}{2} \\ \cos\frac{\psi}{2} \cos\frac{\vartheta}{2} \sin\frac{\gamma}{2} & + & \sin\frac{\psi}{2} \sin\frac{\vartheta}{2} \cos\frac{\gamma}{2} \\ \cos\frac{\psi}{2} \sin\frac{\vartheta}{2} \sin\frac{\gamma}{2} & + & \sin\frac{\psi}{2} \cos\frac{\vartheta}{2} \cos\frac{\gamma}{2} \\ \cos\frac{\psi}{2} \sin\frac{\vartheta}{2} \cos\frac{\gamma}{2} & — & \sin\frac{\psi}{2} \cos\frac{\vartheta}{2} \sin\frac{\gamma}{2} \end{bmatrix} $$display$$
Обратите внимание, если у вас последовательность поворотов другая, то выражения будут тоже другими.
Дуальная часть $inline$\textbf{q}_2$inline$ определяется выражением:
$$display$$\textbf{q}_2 = \frac12 \textbf{r} \otimes \textbf{q}_1$$display$$
Вычисление углов ориентации и вектора положения из бикватерниона. Обратное преобразование
Вычислить углы ориентации можно из действительной части бикватерниона $inline$\textbf{q}_1$inline$:
$$display$$\psi = \arctan{\frac{2(q_0 q_2 — q_1 q_3)}{q_0^2 + q_1^2 — q_2^2 — q_3^2}}$$display$$
$$display$$\vartheta = \arcsin{(2(q_1 q_2 + q_0 q_3))}$$display$$
$$display$$\gamma = \arctan{\frac{2(q_0 q_1 — q_2 q_3)}{q_0^2 — q_1^2 + q_2^2 — q_3^2}}$$display$$
Положение объекта определяется выражением:
$$display$$\textbf{r} = 2 \textbf{q}_2 \otimes \textbf{q}_1^{-1}$$display$$
в результате получается вектор в кватернионной форме $inline$\textbf{r} = (0, r_x, r_y, r_z)^T$inline$
Поворот и перемещение вектора бикватернионом
Одно из замечательных свойств бикватернионов — это поворот и перемещение вектора из одной системы координат в другую. Пусть OoXgYgZg — неподвижная базовая система кординат, а OXYZ — связанная система координат объекта. Тогда ориентацию и положение объекта относительно базовой системы координат можно задать бикватернионом $inline$\widetilde{\textbf{q}}$inline$. Если задан вектор $inline$\textbf{r}$inline$ в связанной системе координат, тогда можно получить вектор $inline$\textbf{r}_0$inline$ в базовой системе координат с помощью формулы:
$$display$$\textbf{r}_0 = \widetilde{\textbf{q}} \otimes \textbf{r} \otimes \widetilde{\textbf{q}}^{-1}$$display$$
и обратно:
$$display$$\textbf{r} = \widetilde{\textbf{q}}^{-1} \otimes \textbf{r}_0 \otimes \widetilde{\textbf{q}}$$display$$
где $inline$\textbf{r}$inline$ — вектор в бикватернионной форме, $inline$\textbf{r} = (1, 0, 0, 0, 0, r_x, r_y, r_z)$inline$
JavaScrip-библиотека работы с бикватернионами
Все вышеперечисленные операции работы с бикватернионами реализованы в javascript-библиотеке, в зависимости от ваших задач ее можно реализовать на других языках программирования. Основные функции работы с бикватернионами:
| Функция | Описание |
|---|---|
DualQuaternion.dq |
Тело бикватерниона в виде массива 8-ми чисел |
DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7) |
Конструктор, который определяет бикватернион путем заданием всех восьми чисел |
DualQuaternion.fromEulerVector(psi, theta, gamma, v) |
Получить бикватернион путем задания ориентации объекта углами Эйлера и вектора положения объекта |
DualQuaternion.getEulerVector() |
Получить углы Эйлера и вектор положения из бикватерниона |
DualQuaternion.getVector() |
Получить вектор положения из бикватерниона |
DualQuaternion.getReal() |
Получить действительную часть бикватерниона (определяет ориентацию объекта в пространстве) |
DualQuaternion.getDual() |
Получить дуальную часть бикватерниона (определяет положение объекта в пространстве) |
DualQuaternion.norm() |
Получить норму бикватерниона в виде дуального числа |
DualQuaternion.mod() |
Получить модуль бикватерниона в виде дуального числа |
DualQuaternion.conjugate() |
Получить сопряженный бикватернион |
DualQuaternion.inverse() |
Получить обратный бикватернион |
DualQuaternion.mul(DQ2) |
Бикватернионное умножение |
DualQuaternion.toString() |
Преобразовать бикватернион в строчку, например, для вывода в отладочную консоль |
/**
*
* Author 2017, Akhramovich A. Sergey (akhramovichsa@gmail.com)
* see https://github.com/infusion/Quaternion.js
*/
// 'use strict';
/**
* Dual Quaternion constructor
*
* @constructor
* @returns {DualQuaternion}
*/
function DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7) {
if (dq0 === undefined) {
this.dq = [1, 0, 0, 0, 0, 0, 0, 0];
} else {
this.dq = [dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7];
}
return this;
};
// Получение кватерниона по углам Эйлера и вектору положения
DualQuaternion['fromEulerVector'] = function(psi, theta, gamma, v) {
var q_real = new Quaternion.fromEuler(psi, theta, gamma);
var q_v = new Quaternion(0, v[0], v[1], v[2]);
var q_dual = q_v.mul(q_real);
return new DualQuaternion(
q_real.q[0], q_real.q[1], q_real.q[2], q_real.q[3],
q_dual.q[0]*0.5, q_dual.q[1]*0.5, q_dual.q[2]*0.5, q_dual.q[3]*0.5);
};
DualQuaternion.prototype = {
'dq': [1, 0, 0, 0, 0, 0, 0, 0],
/**
* Получение углов Эйлера (psi, theta, gamma) и вектора положения из бикватерниона
*/
'getEulerVector': function() {
var euler_angles = this.getReal().getEuler();
var q_dual = this.getDual();
var q_dual_2 = new Quaternion(2.0*q_dual.q[0], 2.0*q_dual.q[1], 2.0*q_dual.q[2], 2.0*q_dual.q[3]);
var q_vector = q_dual_2.mul(this.getReal().conjugate());
return [euler_angles[0], euler_angles[1], euler_angles[2],
q_vector.q[1], q_vector.q[2], q_vector.q[3]];
},
/**
* Получение только вектора положения из бикватерниона
*/
'getVector': function() {
var euler_vector = this.getEulerVector();
return [euler_vector[3], euler_vector[4], euler_vector[5]];
},
/**
* Получить действительную часть бикватерниона
* @returns {Quaternion}
*/
'getReal': function() {
return new Quaternion(this.dq[0], this.dq[1], this.dq[2], this.dq[3]);
},
/**
* Получить дуальную часть бикватерниона
* @returns {Quaternion}
*/
'getDual': function() {
return new Quaternion(this.dq[4], this.dq[5], this.dq[6], this.dq[7]);
},
/**
* Норма бикватерниона
* Внимание! Возвращает дуальное число!
*/
'norm': function() {
return [Math.pow(this.dq[0], 2) + Math.pow(this.dq[1], 2) + Math.pow(this.dq[2], 2) + Math.pow(this.dq[3], 2),
this.dq[0]*this.dq[4] + this.dq[1]*this.dq[5] + this.dq[2]*this.dq[6] + this.dq[3]*this.dq[7]];
},
/**
* Модуль бикватерниона
* Внимание! Возвращает дуальное число!
*/
'mod': function() {
var q_real_mod = Math.sqrt(Math.pow(this.dq[0], 2) + Math.pow(this.dq[1], 2) + Math.pow(this.dq[2], 2) + Math.pow(this.dq[3], 2));
return [q_real_mod,
(this.dq[0]*this.dq[4] + this.dq[1]*this.dq[5] + this.dq[2]*this.dq[6] + this.dq[3]*this.dq[7])/q_real_mod];
},
/**
* Сопряженный бикватернион
* DQ' := (dq0, -dq1, -dq2, -dq3, dq4, -dq5, -dq6, -dq7)
*/
'conjugate': function() {
return new DualQuaternion(this.dq[0], -this.dq[1], -this.dq[2], -this.dq[3], this.dq[4], -this.dq[5], -this.dq[6], -this.dq[7]);
},
// Вычислить обратный бикватернион
'inverse': function() {
var q_real_norm = new Quaternion(this.dq[0], this.dq[1], this.dq[2], this.dq[3]).norm();
var dq_norm_inv = [q_real_norm, - (this.dq[0]*this.dq[4] + this.dq[1]*this.dq[5] + this.dq[2]*this.dq[6] + this.dq[3]*this.dq[7])/q_real_norm];
var dq_conj = this.conjugate();
// Умножение бикватерниона на дуальное число
return new DualQuaternion(
dq_norm_inv[0] * dq_conj.dq[0],
dq_norm_inv[0] * dq_conj.dq[1],
dq_norm_inv[0] * dq_conj.dq[2],
dq_norm_inv[0] * dq_conj.dq[3],
dq_norm_inv[0] * dq_conj.dq[4] + dq_norm_inv[1] * dq_conj.dq[0],
dq_norm_inv[0] * dq_conj.dq[5] + dq_norm_inv[1] * dq_conj.dq[1],
dq_norm_inv[0] * dq_conj.dq[6] + dq_norm_inv[1] * dq_conj.dq[2],
dq_norm_inv[0] * dq_conj.dq[7] + dq_norm_inv[1] * dq_conj.dq[3]);
},
/**
* Бикватернионное умножение
* q1_real*q2_real, q1_real*q2_dual + q1_dual*q2_real
*/
'mul': function(DQ2) {
var q1_real = this.getReal();
var q1_dual = this.getDual();
var q2_real = DQ2.getReal();
var q2_dual = DQ2.getDual();
var q_res_real = q1_real.mul(q2_real);
var q_res_dual_1 = q1_real.mul(q2_dual);
var q_res_dual_2 = q1_dual.mul(q2_real);
return new DualQuaternion(
q_res_real.q[0],
q_res_real.q[1],
q_res_real.q[2],
q_res_real.q[3],
q_res_dual_1.q[0] + q_res_dual_2.q[0],
q_res_dual_1.q[1] + q_res_dual_2.q[1],
q_res_dual_1.q[2] + q_res_dual_2.q[2],
q_res_dual_1.q[3] + q_res_dual_2.q[3]);
},
/**
* Преобразование вектора бикватернионом
*/
'transformVector': function (v) {
var dq_res = this.mul(new DualQuaternion(1, 0, 0, 0, 0, v[0], v[1], v[2])).mul(this.conjugate());
return [dq_res.dq[5], dq_res.dq[6], dq_res.dq[7]];
},
/**
* Преобразовать в строку, для отладки
*/
'toString': function() {
return '[' +
this.dq[0].toString() + ', ' + this.dq[1].toString() + ', ' + this.dq[2].toString() + ', ' + this.dq[3].toString() + ', ' +
this.dq[4].toString() + ', ' + this.dq[5].toString() + ', ' + this.dq[6].toString() + ', ' + this.dq[7].toString() + ']';
}
}
/*
// TEST:
var dq1 = new DualQuaternion.fromEulerVector(0 * Math.PI/180.0, 0 * Math.PI/180, 0 * Math.PI/180, [10, 20, 30]);
console.log(dq1.toString());
console.log('getEulerVector = ', dq1.getEulerVector());
console.log('norm = ', dq1.norm());
console.log('mod = ', dq1.mod());
console.log('conjugate = ', dq1.conjugate().dq);
console.log('inverse = ', dq1.inverse().dq);
var dq2 = new DualQuaternion.fromEulerVector(0 * Math.PI/180.0, 0 * Math.PI/180, 0 * Math.PI/180, [10, 0, 0]);
console.log('mul = ', dq1.mul(dq2).dq);
console.log('transformVector ??? = ', dq1.transformVector([0, 0, 0]));
*/
Пример работы с бикватернионами
Для лучшего понимания основ применения бикватернионов в качестве примера, рассмотрим небольшую игру. Задается прямоугольная область — карта. По карте плавает корабль, на котором установлено поворотное орудие. Здесь необходимо учесть, что для корабля базовая система координат является система координат карты, а для орудия базовая система координат — корабль. Все объекты отрисовываются в системе координат карты и здесь будет интересно увидеть, как можно перейти от системы координат орудия в систему координат карты с помощью свойства бикватернионного умножения. Управление движением корабля осуществляется клавишами W, A, S, D. Направление орудия задается курсором мышки.

Корабль и орудие описываются двумя классами: Ship и Gun. В конструкторе класса корабля задается его форма в виде бикватернионных точек, начальная ориентация и положение на карте в виде бикватерниона this.dq_pos.
Так же заданы бикватернионные приращения при управлении кораблем. При движении вперед-назад (клавиши W, S) будет изменяться только дуальная часть бикватерниона, а при управлении вправо-влево (клавиши A, D) будет меняться действительная и дуальная часть бикватерниона, которая задает угол поворота.
function Ship(ctx, v) {
this.ctx = ctx;
this.dq_pos = new DualQuaternion.fromEulerVector(0*Math.PI/180, 0, 0, v);
// Форма корабля
this.dq_forward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, -10]);
this.dq_forward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, 10]);
this.dq_backward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, -10]);
this.dq_backward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, 10]);
this.dq_forward_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 30, 0, 0]);
// Приращения текущей позиции при управлении
this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]);
this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]);
this.dq_dx_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 1, 0, 0]);
this.dq_dx_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [-1, 0, 0]);
return this;
};
В самом классе реализована только одна функция отрисовки корабля Ship.draw(). Обратите внимание на применение операции бикватернионного умножения каждой точки корабля на бикватернион текущей позицию и ориентации корабля.
Ship.prototype = {
'ctx': 0,
'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, 0, 0, 0),
/**
* Нарисовать кораблик
*/
'draw': function() {
// Переместить все точки кораблика с помощью бикватернионного умножения
v_pos = this.dq_pos.getVector();
v_forward_left = this.dq_pos.mul(this.dq_forward_left).getVector();
v_forward_right = this.dq_pos.mul(this.dq_forward_right).getVector();
v_backward_left = this.dq_pos.mul(this.dq_backward_left).getVector();
v_backward_right = this.dq_pos.mul(this.dq_backward_right).getVector();
v_forward_forward = this.dq_pos.mul(this.dq_forward_forward).getVector();
// Непосредственно рисование
ctx.beginPath();
ctx.moveTo(v_backward_left[0], v_backward_left[2]);
ctx.lineTo(v_forward_left[0], v_forward_left[2]);
ctx.lineTo(v_forward_left[0], v_forward_left[2]);
ctx.lineTo(v_forward_forward[0], v_forward_forward[2]);
ctx.lineTo(v_forward_right[0], v_forward_right[2]);
ctx.lineTo(v_backward_right[0], v_backward_right[2]);
ctx.lineTo(v_backward_left[0], v_backward_left[2]);
ctx.stroke();
ctx.closePath();
}
};
В конструкторе класса орудия задается его форма в виде бикватернионных точек. Орудие будет отображаться в виде линии. Начальная ориентация и положение на корабле задается бикватернионом this.dq_pos. Также задается и привязка к кораблю, на котором оно установлено. Орудие на корабле может только вращаться, поэтому бикватернионные приращения при управлении орудием будут менять только действительную часть бикватерниона, которая задает угол поворота. В данном примере реализовано наведение орудия с помощью курсора мышки, поэтому вращение орудия будет происходить мгновенно.
function Gun(ctx, ship, v) {
this.ctx = ctx;
this.ship = ship;
// Позиция орудия относительно корабля
this.dq_pos = new DualQuaternion.fromEulerVector(0, 0, 0, v);
// Форма орудия
this.dq_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [20, 0, 0]);
this.dq_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 0, 0, 0]);
// Вращение орудия при управлении
this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]);
this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]);
return this;
};
В классе орудия также реализована только одна функция его отрисовки Ship.draw(). Орудие отображается в виде линии, которая задается двумя точками this.dq_backward и this.dq_forward. Для определения координат точек орудия применяется операция бикватернионного умножения.
Gun.prototype = {
'ctx': 0,
'ship': 0,
'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]),
/**
* Нарисовать орудие
*/
'draw': function() {
// Переместить орудие относительно корабля
v_pos = this.ship.dq_pos.getVector();
v_forward = this.ship.dq_pos.mul(this.dq_backward).mul(this.dq_forward).getVector();
v_backward = this.ship.dq_pos.mul(this.dq_backward).getVector();
// Непосредственно рисование
ctx.beginPath();
ctx.moveTo(v_backward[0], v_backward[2]);
ctx.lineTo(v_forward[0], v_forward[2]);
ctx.stroke();
ctx.closePath();
}
};
Обработка управления кораблем и орудием реализована через события. За нажатие и отжатие клавиш управления кораблем отвечают четыре переменные leftPressed, upPressed, rightPressed, downPressed, которые обрабатываются в основном цикле программы.
leftPressed = false;
rightPressed = false;
upPressed = false;
downPressed = false;
dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]);
document.addEventListener("keydown", keyDownHandler, false);
document.addEventListener("keyup", keyUpHandler, false);
document.addEventListener("mousemove", mouseMoveHandler, false);
// Обработка нажатия клавиш управления
function keyDownHandler(e) {
if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = true; } // влево A
else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = true; } // вверх W
else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = true; } // вправо D
else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = true; } // вниз S
}
// Обработка отжатия клавиш управления
function keyUpHandler(e) {
if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = false; } // влево A
else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = false; } // вверх W
else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = false; } // вправо D
else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = false; } // вниз S
}
Одна из самых интересных функций, с точки зрения применения бикватернионных операций, это управление орудием корабля в направлении указателя мышки. Сначала координаты указателя мышки определяются в бикватернион dq_mouse_pos. Затем вычисляется бикватернион положения мышки относительно корабля с помощью бикватернионного умножения. От бикватерниона мышки отнимается бикватернион корабля dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);
(Прим.: операции последовательного бикватернионного умножения читайте справа налево). И наконец, определяется угол между векторами орудия и мышки. Начальной точке орудия gun_1.dq_backward присваивается полученное значение.
function mouseMoveHandler(e) {
var relativeX = e.clientX - canvas.offsetLeft;
var relativeY = e.clientY - canvas.offsetTop;
// Обрабатывать события только когда курсор мышки находится в игровой области
if (relativeX > 0 && relativeX < canvas.width &&
relativeY > 0 && relativeY < canvas.height) {
// Бикватернион положения мышки
dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [relativeX, 0, relativeY]);
// Бикватернион положения мышки относительно корабля
// Направление орудия. От координат мышки отнимается координаты корабля
// Последовательность бикватернионного умножения важна
// DQ_ship^(-1) * DQ_mouse
dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);
// Угол между векторами орудия и мышки
q_gun_mouse = new Quaternion.fromBetweenVectors(gun_1.dq_forward.getVector(), dq_mouse_pos_about_ship.getVector());
dq_gun_mouse = new DualQuaternion(q_gun_mouse.q[0], q_gun_mouse.q[1], q_gun_mouse.q[2], q_gun_mouse.q[3], 0, 0, 0, 0);
gun_1.dq_backward = dq_gun_mouse;
// console.log(dq_gun_mouse.getEulerVector());
// console.log(relativeX + ' ' + relativeY + ' ' + gun_1.dq_forward.toString());
}
}
В основном теле программы инициализируются объекты корабля и орудия ship_1 и gun_1, выводится отладочная информация и осуществляется обработка управления кораблем.
var canvas = document.getElementById("myCanvas");
var ctx = canvas.getContext("2d");
ship_1 = new Ship(ctx, [100, 0, 100]);
gun_1 = new Gun(ctx, ship_1, [0, 0, 0]);
function draw() {
ctx.clearRect(0, 0, canvas.width, canvas.height);
ship_1.draw();
gun_1.draw();
// Debug info
ship_euler_vector = ship_1.dq_pos.getEulerVector();
ship_euler_vector[0] = ship_euler_vector[0]*180/Math.PI;
ship_euler_vector[1] = ship_euler_vector[1]*180/Math.PI;
ship_euler_vector[2] = ship_euler_vector[2]*180/Math.PI;
ship_euler_vector = ship_euler_vector.map(function(each_element){ return each_element.toFixed(2); });
ship_dq = ship_1.dq_pos.dq.map(function(each_element){ return each_element.toFixed(2); });
gun_dq = ship_1.dq_pos.mul(gun_1.dq_backward).dq.map(function(each_element){ return each_element.toFixed(2); });
ctx.font = "8pt Courier";
ctx.fillText("Ship: " + ship_dq + " | psi, theta, gamma, vector:" + ship_euler_vector, 10, 20);
ctx.fillText("Gun: " + gun_dq, 10, 40);
// Управление корабликом
if (leftPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_left); }
if (rightPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_right); }
if (upPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_forward); }
if (downPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_backward); }
requestAnimationFrame(draw);
}
draw();
В ссылке на архив содержится полный код библиотек работы с кватернионами и бикватернионами, сам скрипт программы и файл index.html, который можно открыть локально в браузере, для того чтобы запустить рассмотренный выше пример.
Пример работы с бикватернионами
Заключение
У вас может возникнуть вопрос: зачем применять такой сложный математический аппарат, когда можно обойтись стандартными средствами для перемещения и вращения объектов? Одним из основных преимуществ заключается в том, что бикватернионная форма записи является более эффективной в вычислительном плане, так как все операции работы с бикватернионами после раскрытия выражений являются линейными. В данном видео Geometric Skinning with Approximate Dual Quaternion Blending показано насколько эффективнее вычисления с использованием бикватернионов в сравнении с другими методами.
Информацию по применению бикватернионов я в основном брал из англоязычных источников.
Из отечественной литературы я могу посоветовать две книги:
- Челноков Юрий Николаевич. Кватернионные и бикватернионные модели и методы механики твердого тела и их приложения. Геометрия и кинематика движения. — монументальный теоретический труд.
- Гордеев Вадим Николаевич. Кватернионы и бикватернионы с приложениями в геометрии и механике. — написана более понятным языком и показаны применения в задачах формообразования криволинейных пространственных структур.
