[Перевод] 30.000$ за решение задач о Правиле 30 для клеточных автоматов — конкурс от Стивена Вольфрама

Оригинал перевода в моём личном блоге
Поясним для читателей, что означает «Правило 30» — это элементарный клеточный автомат (см. Wiki), состояние которого (правило построения нового уровня ячеек на основе старого) в двоичной системе счисления задается как 0–0–0–1–1–1–1–0, что можно интерпретировать как 30 в десятичной системе счисления.
Итак, с чего все началось? — «Правило 30»
Как может быть так, что что-то невероятно простое производит на свет что-то невероятно сложное? Прошло уже почти 40 лет с того момента, как я впервые познакомился с Правилом 30, но оно до сих пор поражает меня и приводит в восторг. На долгое время оно стало моим личным любимым открытием в истории науки, за эти годы оно изменило все мое мировоззрение и привело меня к разнообразным новым типам понимания науки, технологий, философии и многому другому.
Но даже спустя столько лет существует еще много базовых понятий о Правиле 30, которые остаются для нас недоступными. И поэтому я решил, что пришло время сделать все возможное, чтобы стимулировать процесс выявления основного набора этих базовых закономерностей.
Итак, сегодня я предлагаю соискателям 30000 долларов США в качестве общей суммы призов за ответы на три основных вопроса о Правиле 30.
Правило 30 чрезвычайно просто:
Существует последовательность строк черных и белых клеток (ячеек) и, учитывая конкретную строку чёрно-белых ячеек, определяются цвета ячеек в строке ниже, рассматривая каждую ячейку в отдельности и ее смежных соседних ячеек, затем к ним применяется следующее простое правило подстановки, а именно:
Код
RulePlot[CellularAutomaton[30]]
Что произойдет если начать с одной черной клетки? [Берется ряд из белых клеток, бесконечный в обе стороны и одна черная клетка, затем к этому ряду применяются правила, показанные выше, получается новый ряд и т. д. — примечание переводчика] Допустим, (как это сделал я сам сначала), что правило это достаточно простое, и шаблон, который получается на основе его работы, должен быть соответственно тоже простым. Однако если вы проведете эксперимент, то увидите, что получится после первых 50-ти шагов работы алгоритма:

RulePlot[CellularAutomaton[30], {{1}, 0}, 50, Mesh -> All,
ImageSize -> Full]
Естественно можно предположить, что в итоге работы алгоритма в итоге получится гораздо более простой математический объект. Однако вот что происходит после первых 300 шагов:

Отсюда видно, что появляется некоторая закономерность — с левой стороны пирамиды. Но при этом многие аспекты этого шаблона выглядят как нечто образованное случайным образом.
Непостижимо, что такое простое правило может в итоге привести к такому сложному поведению системы. На основе этого я пришел к выводу что в вычислительной вселенной всех возможных компьютерных программ такое поведение достаточно распространено, даже более того встречается практически везде.
На основе этой гипотезы я разработал подход к формированию науки совершенно нового типа — на базе принципов наблюдения за работой простых алгоритмов.
Постепенно накапливалось все больше доказательств этих принципов.
Однако вернемся к Правилу 30 и рассмотрим предметно, что именно оно нам позволяет делать, и в чем его польза? Что конкретно можно сказать о поведении данного алгоритма? Сразу бросается в глаза, что даже ответы на самые очевидные вопросы оказываются сложными.
Даже после десятилетий, за которые не было найдено ответов, я решил, что пришло время задать некоторые конкретные вопросы о Правиле 30, при этом простимулировав данное направление серьезными денежными призами.
Я уже пытался делать нечто подобное в 2007 году, назначив премию за ответ на основной вопрос о конкретной машине Тьюринга. И в данном случае результат был положительным и не заставил себя долго ждать. Всего через несколько месяцев этот приз был выигран — при этом навсегда установив, что из себя представляет простейшая из возможных универсальных машин Тьюринга, а также весьма убедительно доказав общий принцип вычислительной эквивалентности, разработанный ранее мной лично.
Конкурс по Правилу 30 снова ставит перед собой целью решение ключевой задачи, а именно: насколько сложным является поведение Правила 30? Каждая из задач ставит вопрос в этой области по-своему и конкретно. Как и само Правило 30, все они обманчиво просты в своей изначальной постановке. И все же решение любого из них будет огромным достижением, которое в итоге поможет осветить фундаментальные принципы свойств формирования вычислительной вселенной, которые выходят далеко за пределы специфики Правила 30.
Я работал над каждой из этих проблем более 35 лет. И все это время я пытался найти правильную идею в рамках непротиворечивого математического или вычислительного мышления, с целью наконец-то разрешить хотя бы одну из этих задач. Сейчас я хочу открыть этот процесс для обозрения всего мирового сообщества. Вместе с тем мне интересно будет узнать, чего можно достичь в решении данных вопросов, и какие методы при этом могут быть использованы.
Правило 30 — задачи для решения
Что касается конкурсных задач по Правилу 30, я ставлю в приоритет одну из ключевых особенностей работы алгоритма Правила 30, а именно: очевидную случайность формирования ячеек его центрального столбца. Начните с одной черной ячейки, затем проведите взглядом по последовательности значений цветов ячеек этого столбца и вы придете к выводу, что они случайны:

ArrayPlot[
MapIndexed[If[#2[[2]] != 21, # /. {0 -> 0.2, 1 -> .6}, #] &,
CellularAutomaton[30, {{1}, 0}, 20], {2}], Mesh -> All]
Но в каком смысле они «действительно случайные»? И можно ли это предположение доказать? Каждая из поставленных задач в рамках проводимого конкурса использует свой критерий случайности, а после этого задает вопрос, является ли последовательность случайной в соответствии с этим критерием.
Задача 1: всегда ли центральный столбец остается непериодическим?
Рассмотрим начало центрального столбца Правила 30:

ArrayPlot[List@CellularAutomaton[30, {{1}, 0}, {80, {{0}}}],
Mesh -> True, ImageSize -> Full]
Не трудно обнаружить, что значения в данном столбце не повторяются — он не является периодическим. Но задача заключается в том, станет ли центральный столбец периодическим вообще когда-нибудь? Запустив Правило 30, мы видим, что последовательность не становится периодической даже в первом миллиарде шагов. Что же необходимо сделать, для того, чтобы доподлинно установить и доказать это.
Вот ссылка где находится первый миллион и первый миллиард значений данной последовательности (хранилище данных Wolfram).
Задача 2: Встречается ли каждый цвет ячейки (черный или белый) в среднем с равной вероятностью в центральной столбце?
Вот что мы получим на выходе, если подсчитаем количество черных и белых ячеек последовательно на большем количестве шагов в центральном столбце алгоритма Правила 30:

Dataset[{{1, 1, 0, ""}, {10, 7, 3, 2.3333333333333335}, {100, 52, 48, 1.0833333333333333},
{1000, 481, 519, 0.9267822736030829}, {10000, 5032, 4968, 1.0128824476650564},
{100000, 50098, 49902, 1.0039276982886458}, {1000000, 500768, 499232,
1.003076725850907}, {10000000, 5002220, 4997780, 1.0008883944471345},
{100000000, 50009976, 49990024, 1.000399119632349},
{1000000000, 500025038, 499974962, 1.0001001570154626}}]
Результаты, безусловно, близки к равным для черных и белых ячеек. Здесь проблемным (вопросом задачи) является вопрос сходится ли это отношение к 1 при повышении числа шагов цикла.
Задача 3: Требует ли вычисление n-й ячейки центрального столбца хотя бы O (n) операций?
Чтобы найти n-ю ячейку в центральном столбце, всегда можно просто запустить Правило 30 для n шагов, вычисляя значения всех ячеек внутри выделенного на рисунке ниже ромба:

With[{n = 100},
ArrayPlot[
MapIndexed[If[Total[Abs[#2 - n/2 - 1]] <= n/2, #, #/4] &,
CellularAutomaton[30, CenterArray[{1}, n + 1], n], {2}]]]
Но если сделать это напрямую, выполнится 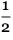 n2 отдельных обновлений ячейки, поэтому требуемые вычислительные мощности возрастают как O (n2). Вопрос данной задачи — существует ли более (или самый) быстрый метод вычисления значения n-й ячейки без всех промежуточных вычислений — или, в частности, менее чем за O (n) операций.
n2 отдельных обновлений ячейки, поэтому требуемые вычислительные мощности возрастают как O (n2). Вопрос данной задачи — существует ли более (или самый) быстрый метод вычисления значения n-й ячейки без всех промежуточных вычислений — или, в частности, менее чем за O (n) операций.
Цифры из которых состоит число Пи
Правило 30 есть порождение вычислительной вселенной: система, основанная на исследовании возможных простых программ с новой интеллектуальной структурой, которую обеспечивает парадигма вычислений. Однако у задач, которые я определил в конкурсе для Правила 30, есть аналоги и в математике, которым уже много веков.
Рассмотрим значения цифр в числе Пи. Поведение этих цифр является похожим на генерирование данных в центральном столбце алгоритма Правила 30. То есть существует заданный алгоритм их вычисления, при этом, однажды сформулированные, они кажутся практически случайными под любые задачи.
![N[Pi, 85]](https://habrastorage.org/getpro/habr/post_images/49e/ae6/17d/49eae617de3c0c9a864d4624413c6ce8.png)
N[Pi, 85]
Просто чтобы сделать аналог немного ближе, вот первые несколько цифр Пи в системе счисления с основанием 2:
![BaseForm[N[Pi, 25], 2]](https://habrastorage.org/getpro/habr/post_images/18e/d4b/8f6/18ed4b8f6fd778443cc62470ea0956a9.png)
BaseForm[N[Pi, 25], 2]
И вот первые несколько битов в центральном столбце Правила 30:
![Row[CellularAutomaton[30, {{1}, 0}, {90, {{0}}}]]](https://habrastorage.org/getpro/habr/post_images/9e9/f64/a52/9e9f64a521480621d3adbb859609742a.png)
Row[CellularAutomaton[30, {{1}, 0}, {90, {{0}}}]]
Ради интереса можно преобразовать их десятичную форму:
![N[FromDigits[{Flatten[CellularAutomaton[30, {{1}, 0}, {500, {0}}]], 0}, 2], 85]](https://habrastorage.org/getpro/habr/post_images/0df/d67/782/0dfd677828ca278c971d267948d88ad3.png)
N[FromDigits[{Flatten[CellularAutomaton[30, {{1}, 0}, {500, {0}}]],
0}, 2], 85]
Конечно, известные алгоритмы вычисления цифр числа Пи значительно сложнее, чем сравнительно простое правило генерации ячеек центрального столбца Правила 30. Итак, что же нам известно о цифрах в числе Пи?
Во-первых, нам известно, что они не повторяются. Это было доказано еще в 60-х годах 18-го века, когда было показано что Пи — является иррациональным числом, поскольку единственные числа, цифры в которых повторяются, являются рациональными числами. (В 1882 году было также показано, что Пи трансцендентно, то есть, что его нельзя выразить через корни многочленов).
Так какую же здесь аналогию можно провести с постановкой задачи 2? Знаем ли мы, что в последовательности цифр числа Пи разные цифры встречаются с одинаковой частотой? К настоящему времени было вычислено более 100 триллионов двоичных цифр — и измеренные частоты цифр очень близки (в первых 40 триллионах двоичных цифр числа Пи отношение Единиц к Нулям составляет примерно 0,99999998064). Но при вычислении предела, будут ли частоты точно такими же? Ученые задавались этим вопросом в течение нескольких веков, но до сих пор математика не смогла дать на него ответа.
Для рациональных чисел последовательности цифр, из которых они состоят, являются периодическими, и при этом легко определить относительные частоты появления этих цифр в числе. Однако для последовательности цифр всех прочих «созданных природой (естественно построенных)» чисел, в большинстве случаев, практически ничего не известно о том к чему стремятся частоты цифр, входящих в число. Логично было бы предположить, что на самом деле цифры числа Пи (а также центральный столбец Правила 30) являются «нормальными» в том смысле, что не только каждая отдельная цифра, но и любой блок цифр заданной длины встречаются с равной предельной частотой. И, как было отмечено в работах по этой тематике 1930-х годов, вполне возможно «построить цифровую конструкцию (модель)» нормальных чисел. Постоянная Чемперноуна, полученная путем объединения цифр последовательных целых чисел, является примером вышесказанного рассуждения (это же можно получить на базе любого нормального числа, объединяя значения функций последовательных целых чисел):
![N[ChampernowneNumber[10], 85]](https://habrastorage.org/getpro/habr/post_images/253/f93/8f3/253f938f3261e70f8985a49bf1158dde.png)
N[ChampernowneNumber[10], 85]
Следует отметить, что здесь дело в том, что для «естественно построенных» чисел, образованных за счет комбинаций стандартных математических функций, не известно ни одного обнаруженного примера, где бы была найдена какая-либо регулярная последовательность цифр. Естественно, в конечном итоге данное положение зависит от того, что подразумевать под «регулярностью», и на каком-то этапе задача превращается в своего рода цифро-аналоговый поиск внеземного разума. При этом отсутствуют доказательства того, что не существует возможности, например, найти какую-то сложную комбинацию квадратных корней, которая имела бы последовательность цифр с некоторой весьма очевидной регулярностью.
Итак, рассмотрим, наконец, аналог задачи 3 для Пи? В отличие от Правила 30, где очевидным способом вычисления элементов в последовательности является один шаг за раз, традиционные способы вычисления цифр числа Пи включают в себя получение лучших приближений к Пи как к точному числу. Со стандартным («причудливым») рядом, изобретенным Рамануджаном в 1910 году и улучшенным братьями Чудновскими в 1989 году, первые несколько членов этой серии дают следующие приближения:

Style[Table[N[(12*\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(n\)]
\*FractionBox[\(
\*SuperscriptBox[\((\(-1\))\), \(k\)]*\(\((6*k)\)!\)*\((13591409 +
545140134*k)\)\), \(\(\((3*k)\)!\)
\*SuperscriptBox[\((\(k!\))\), \(3\)]*
\*SuperscriptBox[\(640320\), \(3*k + 3/2\)]\)]\))^-1, 100], {n, 10}] //
Column, 9]
Так сколько же операций необходимо для того чтобы найти n-ю цифру? Число слагаемых, требуемых в ряду, равно O (n). Но каждое условие должно быть вычислено с n-значной точностью, которая требует, по меньшей мере O (n) отдельных вычислительных операций, подразумевающих, что в целом вычислительные трудозатраты будут больше, чем O (n).
До 1990-х годов предполагалось, что не существует никакого способа вычислить n-ю цифру Пи без вычисления всех предыдущих. Но в 1995 году Саймон Плуфф обнаружил, что на самом деле можно вычислить, хотя и с некоторой вероятностью, n-ю цифру, не вычисляя предыдущие. И хотя можно было бы подумать, что это позволит получить n-ю цифру меньше, чем за O (n) операций, тот факт, что нужно выполнять вычисления с точностью n-цифр, означает, что по крайней мере по прежнему требуется O (n) операций.
Результаты, аналогии и интуиция
Задача 1: всегда ли центральный столбец остается непериодическим?
Из трех призов конкурса Правила 30 это тот, в котором большая часть прогресса в решении данного вопроса в настоящий момент уже достигнута. Поскольку до сих пор неизвестно, станет ли центральный столбец Правила 30 периодическим, Эрика Джен в 1986 году показала, что никакие два столбца не могут быть периодическими. И на самом деле это так, и можно также привести аргументы в пользу того, что один столбец в сочетании с отдельными ячейками в другом столбце не могут быть периодическими.
Доказательство о паре столбцов использует особенность Правила 30. Рассмотрим структуру правила:
![RulePlot[CellularAutomaton[30]]](https://habrastorage.org/getpro/habr/post_images/5fa/ca7/858/5faca785893d90e7969ef2a4dad73c58.png)
RulePlot[CellularAutomaton[30]]
Существует возможность просто сказать, что для каждой тройки ячеек правило определяет цвет центральной ячейки по ней, но для Правила 30 можно также эффективно выполнять правило вбок: с учетом ячейки справа и выше можно также однозначно определить цвет ячейки слева. Это означает, что если взять два смежных столбца, можно восстановить весь шаблон слева:

GraphicsRow[
ArrayPlot[#, PlotRange -> 1, Mesh -> All, PlotRange -> 1,
Background -> LightGray,
ImageSize -> {Automatic, 80}] & /@ (PadLeft[#, {Length[#], 10},
10] & /@
Module[{data = {{0, 1}, {1, 1}, {0, 0}, {0, 1}, {1, 1}, {1,
0}, {0, 1}, {1, 10}}},
Flatten[{{data},
Table[Join[
Table[Module[{p, q = data[[n, 1]], r = data[[n, 2]],
s = data[[n + 1, 1]] },
p = Mod[-q - r - q r + s, 2];
PrependTo[data[[n]], p]], {n, 1, Length[data] - i}],
PrependTo[data[[-#]], 10] & /@ Reverse[Range[i]]], {i, 7}]},
1]])]
Однако если бы столбцы имели периодическую структуру, из этого сразу бы следовало, что восстановленный шаблон также должен быть периодическим. Так, например, по построению, по крайней мере, начальные условия точно не являются периодическим, и, следовательно, оба столбца не могут быть периодическими. Это же утверждение справедливо, если столбцы не являются смежными, и если не известны все ячейки в обоих столбцах. При этом не существует никакого известного способа распространить это положение для одного столбца, такого как центральный столбец, и, таким образом, оно не решает первую задачу конкурса по Правилу 30.
Итак, что же может быть использовано при его решении? Если выяснится, что центральный столбец в конечном итоге является периодическим, можно было бы просто его вычислить. Нам известно, что он не является периодическим для первых миллиардов шагов, но можно, по крайней мере, предположить, что может существовать переходный процесс с триллионами шагов, после которого он станет периодическим.
Как вы считаете, это правдоподобно? Переходные процессы случаются — и теоретически (как и в классической задаче остановки машины Тьюринга) они могут быть даже произвольной длины. Здесь рассмотрим некоторый пример — найденный при поиске — Правила с 4-мя возможными цветами (общий код 150898). Предположим, мы запустим его на 200 шагов, при этом, как видно, центральный столбец будет являться совершенно случайным:

ArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {200, 150 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]},
PixelConstrained -> 2, Frame -> False]
После 500 шагов весь шаблон выглядит совершенно случайно:

ArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {500, 300 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, Frame -> False,
ImagePadding -> 0, PlotRangePadding -> 0, PixelConstrained -> 1]
Здесь видно, что при приближении к центральному столбцу, происходит нечто удивительное: после 251 шага центральный столбец, кажется, перерождается до фиксированного значения (или, по крайней мере, фиксируется на последующие более чем миллион шагов):

Grid[{ArrayPlot[#, Mesh -> True,
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, ImageSize -> 38,
MeshStyle -> Lighter[GrayLevel[.5, .65], .45]] & /@
Partition[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {1400, {-4, 4}}],
100]}, Spacings -> .35]
Может ли такой же переходный процесс произойти и в Правиле 30? Рассмотрим шаблоны из Правила 30, и выделим те, где диагонали слева имеют периодичность:

steps = 500;
diagonalsofrule30 =
Reverse /@
Transpose[
MapIndexed[RotateLeft[#1, (steps + 1) - #2[[1]]] &,
CellularAutomaton[30, {{1}, 0}, steps]]];diagonaldataofrule30 =
Table[With[{split =
Split[Partition[Drop[diagonalsofrule30[[k]], 1], 8]],
ones = Flatten[
Position[Reverse[Drop[diagonalsofrule30[[k]], 1]],
1]]}, {Length[split[[1]]], split[[1, 1]],
If[Length[split] > 1, split[[2, 1]],
Length[diagonalsofrule30[[k]]] - Floor[k/2]]}], {k, 1,
2 steps + 1}];
transientdiagonalrule30 = %;
transitionpointofrule30 =
If[IntegerQ[#[[3]]], #[[3]],
If[#[[1]] > 1,
8 #[[1]] + Count[Split[#[[2]] - #[[3]]][[1]], 0] + 1, 0] ] & /@
diagonaldataofrule30;
decreasingtransitionpointofrule30 =
Append[Min /@ Partition[transitionpointofrule30, 2, 1], 0];
transitioneddiagonalsofrule30 =
Table[Join[
Take[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]] + 2,
Drop[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]]], {n, 1, 2 steps + 1}];
transientdiagonalrule30 =
MapIndexed[RotateRight[#1, (steps + 1) - #2[[1]]] &,
Transpose[Reverse /@ transitioneddiagonalsofrule30]];
smallertransientdiagonalrule30 =
Take[#, {225, 775}] & /@ Take[transientdiagonalrule30, 275];
Framed[ArrayPlot[smallertransientdiagonalrule30,
ColorRules -> {0 -> White, 1 -> Gray, 2 -> Hue[0.14, 0.55, 1],
3 -> Hue[0.07, 1, 1]}, PixelConstrained -> 1,
Frame -> None,
ImagePadding -> 0, ImageMargins -> 0,
PlotRangePadding -> 0, PlotRangePadding -> Full
], FrameMargins -> 0, FrameStyle -> GrayLevel[.75]]
По всей видимости, здесь существует граница, которая отделяет порядок слева от беспорядка справа. И, по крайней мере, за первые 100 000 шагов или около того, кажется, что граница смещается в среднем примерно на 0,252 шага влево на каждом шаге — с некоторыми случайными отклонениями:
data = CloudGet[
CloudObject[
"https://www.wolframcloud.com/obj/bc470188-f629-4497-965d-\
a10fe057e2fd"]];ListLinePlot[
MapIndexed[{First[#2], -# - .252 First[#2]} &,
Module[{m = -1, w},
w = If[First[#] > m, m = First[#], m] & /@ data[[1]]; m = 1;
Table[While[w[[m]] < i, m++]; m - i, {i, 100000}]]],
Filling -> Axis, AspectRatio -> 1/4, MaxPlotPoints -> 10000,
Frame -> True, PlotRangePadding -> 0, AxesOrigin -> {Automatic, 0},
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
Но как же мы в итоге узнаем, в какой момент эти колебания перестанут быть значительными, настолько, что заставят порядок слева пересекать центральный столбец и, возможно, даже сделают весь шаблон периодическим? Судя по имеющимся данным, предположение выглядит маловероятным, при этом я точно не могу сказать, как это можно определить.
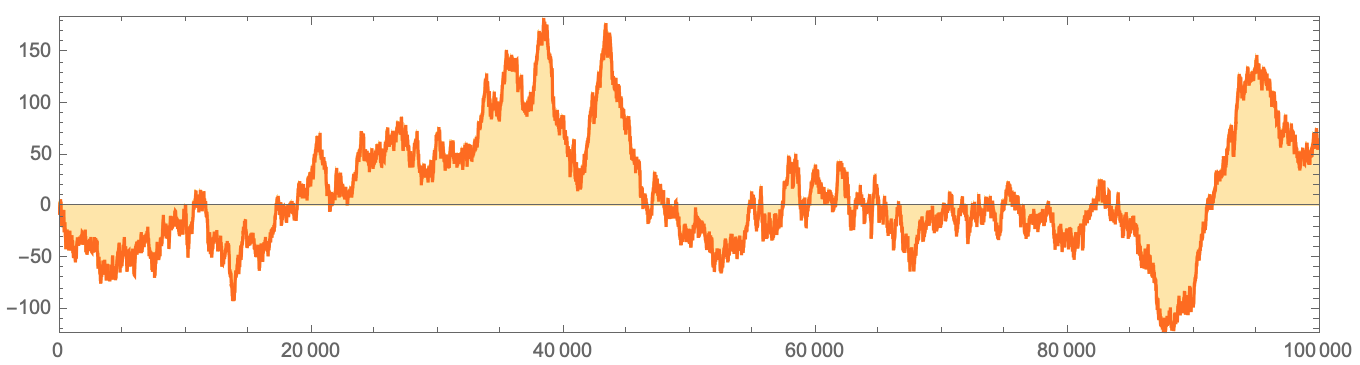
Это, безусловно, именно тот случай, который иллюстрирует существование систем с исключительно длинными «переходными процессами». Теперь рассмотрим распределение простых чисел и вычислим LogIntegral[n] — PrimePi[n]
DiscretePlot[LogIntegral[n] - PrimePi[n], {n, 10000},
Filling -> Axis,
Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4,
Joined -> True, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
Да, колебания присутствуют, но на данной иллюстрации это выглядит так, как будто бы эта разница всегда будет в положительной области. И это, например, то, о чем рассуждал Рамануджан, но в итоге оказывается, что это не так. В начале граница того, где он потерпел неудачу, была, для того времени, астрономически большой (число Скивса 101010964). И хотя до сих пор никто не нашел явного значения n, для которого разность отрицательна, известно, что до n=10317 она должна существовать (и в конечном итоге разность будет отрицательной).
У меня сформировалось мнение, что ничего подобного не происходит с центральным столбцом Правила 30, но пока у нас нет доказательств того, что это невозможно, утверждать этого нельзя.
Следует отметить, что существует возможность сделать предположение, что хотя принципиально и существует возможность доказать периодичность, раскрывая регулярность в центральном столбце Правила 30, ничего подобного не будет возможно проделать для непериодичности. Известно, что существуют шаблоны, центральные столбцы которых непериодические, хотя они и являются весьма регулярными. Основным классом таких примеров являются вложенные шаблоны. Вот, например, очень простая иллюстрация из Правила 161, в котором центральный столбец имеет белые ячейки, когда n=2k:

GraphicsRow[
ArrayPlot[CellularAutomaton[161, {{1}, 0}, #]] & /@ {40, 200}]
А вот еще немного более сложный пример (из 2-цветного Правила 69540422 для двух соседей), в котором центральный столбец является последовательностью Туэ–Морса — ThueMorse[n]:

GraphicsRow[
ArrayPlot[
CellularAutomaton[{69540422, 2, 2}, {{1},
0}, {#, {-#, #}}]] & /@ {40, 400}]
Можно считать, что последовательность Туэ–Морса генерируется последовательным применением замены:

RulePlot[SubstitutionSystem[{0 -> {0, 1}, 1 -> {1, 0}}],
Appearance -> "Arrow"]
Оказывается n-й член в этой последовательности задается как Mod[DigitCount[n, 2, 1], 2] — данный объект никогда не будет являться периодическим.
Может ли получиться так, что центральный столбец Правила 30 может быть сгенерирован посредством замены? Если это так, то я был бы поражен этим фактом (хотя существуют, казалось бы, естественные примеры, когда появляются очень сложные системы замещения), но опять же, пока не существует доказательств этого.
Следует отметить, что все конкурсные задачи из Правила 30 рассматриваются в постановке алгоритма, работающего на бесконечном множестве клеток. Но что, если попробовать рассматривать только n ячеек, скажем, с периодическими граничными условиями (то есть брать правого соседа самой правой ячейки в качестве самой левой ячейки и наоборот)? При этом очевидно, что существует 2n возможных полных состояний системы — и можно построить диаграмму состояний перехода, которая будет показывать, какое одно состояние развивается до какого другого. Рассмотрим диаграмму для n=5:

Graph[# -> CellularAutomaton[30][#] & /@ Tuples[{1, 0}, 4],
VertexLabels -> ((# ->
ArrayPlot[{#}, ImageSize -> 30, Mesh -> True]) & /@
Tuples[{1, 0}, 4])]
И вот это для n=4 до n=11:

Row[Table[
Framed[Graph[# -> CellularAutomaton[30][#] & /@
Tuples[{1, 0}, n]]], {n, 4, 11}]]
Структура ее заключается в том, что существует группа состояний, которые появляются только как переходные процессы, вместе с другими состояниями, которые находятся в циклах. Неизбежно, что цикл не может быть длиннее 2n (на самом деле, соображения симметрии показывают, что он всегда должен быть несколько меньше).
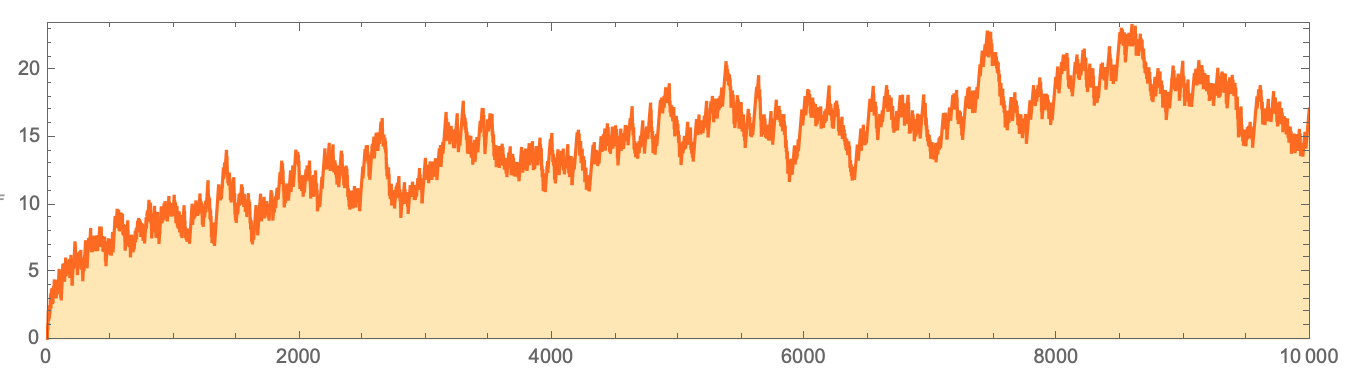
Итак, в массиве размера n Правило 30 всегда должно показывать поведение, которое становится периодическим с периодом, который меньше 2n. Вот длины существующих периодов, начинающихся с начального условия одной черной ячейки (график постороен в логарифмическом масштабе):
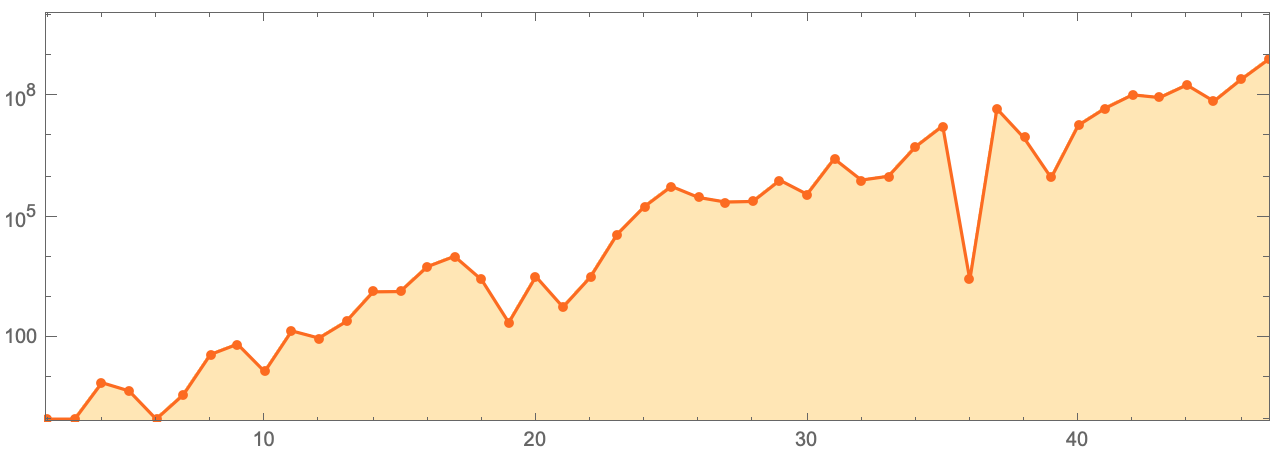
ListLogPlot[
Normal[Values[
ResourceData[
"Repetition Periods for Elementary Cellular Automata"][
Select[#Rule == 30 &]][All, "RepetitionPeriods"]]],
Joined -> True, Filling -> Bottom, Mesh -> All,
MeshStyle -> PointSize[.008], AspectRatio -> 1/3, Frame -> True,
PlotRange -> {{47, 2}, {0, 10^10}}, PlotRangePadding -> .1,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
И, по крайней мере, для этих значений n период довольно хорошо аппроксимиуется функцией 20.63n. И да, по крайней мере, во всех этих случаях период центрального столбца равен периоду общей эволюции клеточного автомата. Но что означают эти результаты для конечного размера в случае распространения выводов, полученных на их основе, на совокупности ячеек бесконечного размера? Ответ не является очевидным и тривиальным.
Задача 2: Встречается ли в среднем каждый цвет ячейки с одинаковой частотой в центральной колонке или нет?
Рассмотрим график отклонений количества Единиц от Нулей на 10000 шагах центрального столбца Правила 30:
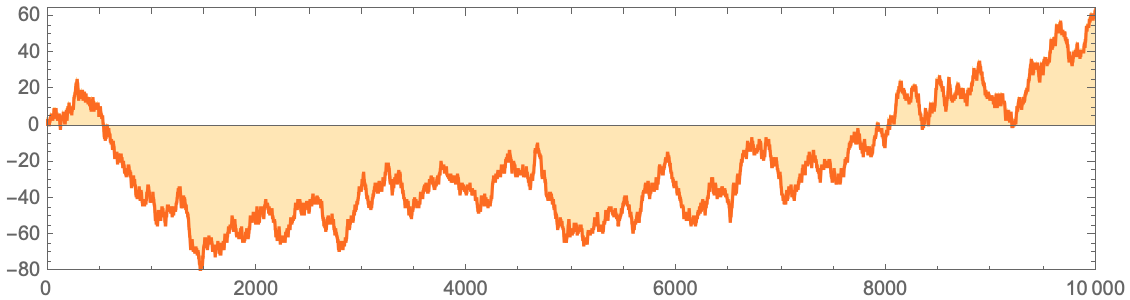
RListLinePlot[
Accumulate[2 CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}] - 1],
AspectRatio -> 1/4, Frame -> True, PlotRangePadding -> 0,
AxesOrigin -> {Automatic, 0}, Filling -> Axis,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
За миллион шагов:
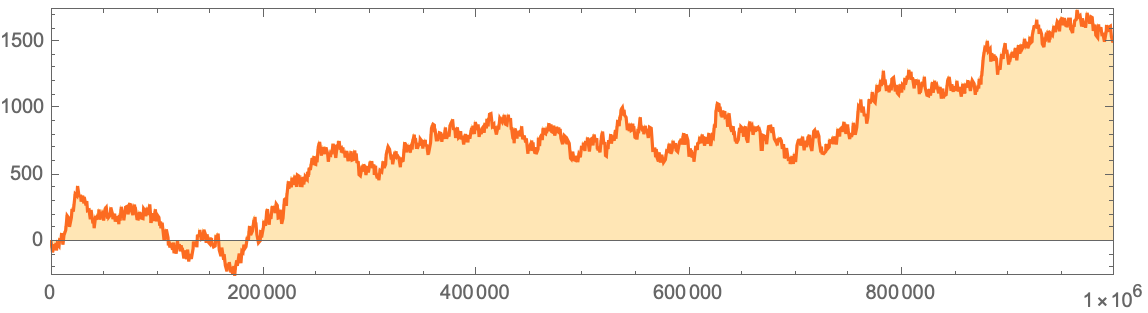
ListLinePlot[
Accumulate[
2 ResourceData[
"A Million Bits of the Center Column of the Rule 30 Cellular Automaton"] - 1], Filling -> Axis, Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4, MaxPlotPoints -> 1000, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
И миллиард шагов:
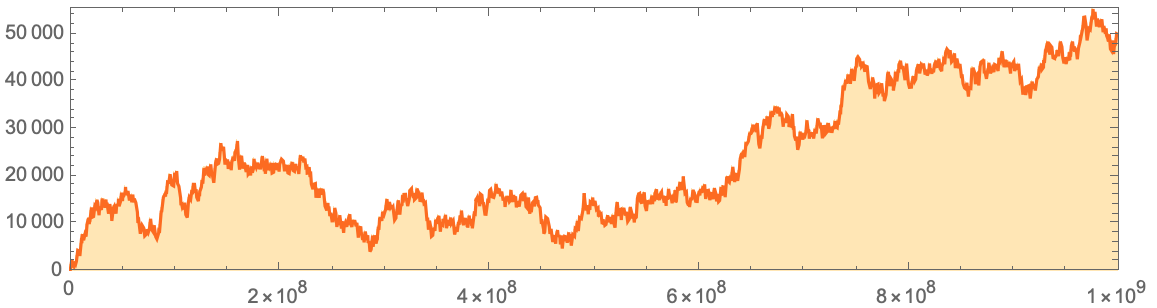
data=Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]];
data=Accumulate[2 data-1];
sdata=Downsample[data,10^5];
ListLinePlot[Transpose[{Range[10000] 10^5,sdata}],Filling->Axis,Frame->True,PlotRangePadding->0,AspectRatio->1/4,MaxPlotPoints->1000,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]
На основе этих данных можно увидеть, что существуют случаи, когда есть превышение количества 1 (единиц) над 0 (нулями), и наоборот, хотя, по мере приближения к миллиарду шагов количество Единиц, кажется, выигрывает у Нулей, по крайней мере, на данный момент.
Так давайте же вычислим отношение общего числа Единиц к общему числу Нулей. Вот такая картина у нас получится после 10 000 шагов:

Quiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.88, 1.04}}]]
Как вы считаете, приближается ли это к значению 1? Сложно сказать…
Давайте продвинемся немного дальше, и вот что мы увидим:
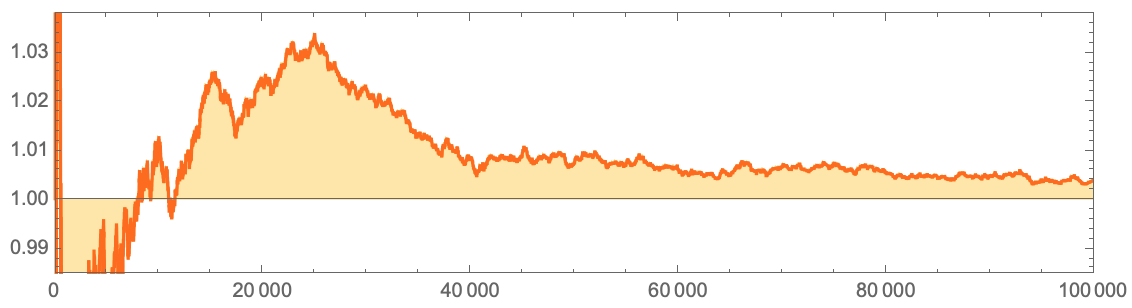
Quiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^5 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.985, 1.038}}]]
Отклонение становится все меньше, но все еще трудно сказать, что произойдет в итоге. Построение отклонения отношения количества Единиц и Нулей от 1 на графике при миллиарде шагов позволяет предположить, что оно систематически уменьшается:
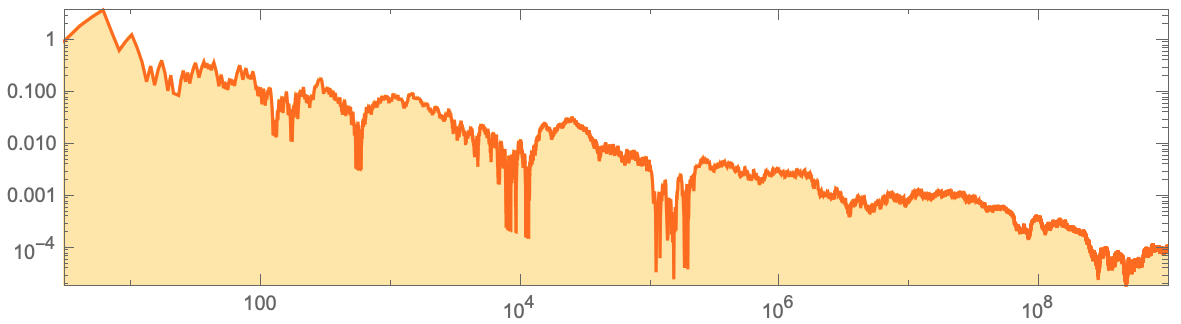
accdata=Accumulate[Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]]];diffratio=FunctionCompile[Function[Typed[arg,TypeSpecifier["PackedArray"]["MachineInteger",1]],MapIndexed[Abs[N[#]/(First[#2]-N[#])-1.]&,arg]]];
data=diffratio[accdata];
ListLogLogPlot[Join[Transpose[{Range[3,10^5],data[[3;;10^5]]}],Transpose[{Range[10^5+1000,10^9,1000],data[[10^5+1000;;10^9;;1000]]}]],Joined->True,AspectRatio->1/4,Frame->True,Filling->Axis,PlotRangePadding->0,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]
Как можно быть уверенными, что эта тенденция сохранится? На данный момент у нас не может быть такой убежденности. И действительно, все может оказаться довольно плохо. Возможно, колебания Единиц против Нулей увеличиваются, поэтому, даже если мы усредняем по более длинным последовательностям, общее соотношение никогда не сойдется до определенного значения.
Опять же, у меня существуют сомнения, что это произойдет в центральном столбце Правила 30, но без доказательств мы не можем знать этого наверняка.
Здесь мы рассматриваем частоты появления черных и белых клеток, но очевидное здесь обобщение состоит в том, чтобы задать вместо этого вопрос о частотах для блоков ячеек длины k. Мы можем рассмотреть вопрос, все ли 2k таких блоков имеют одинаковую предельную частоту или нет. Или мы можем задать более простой вопрос о том, встречаются ли когда-либо все из этих блоков, или, другими словами, если один блок заходит достаточно далеко, центральный столбец Правила 30 будет содержать любую данную последовательность длины k (допустим побитовое представление некоего литературного произведения).
В крайнем случае, здесь мы можем получить эмпирические доказательства. Например, по крайней мере, до k=22, все 2k последовательностей имеют место быть, и вот сколько шагов нужно, чтобы подтвердить это:

ListLogPlot[{3, 7, 13, 63, 116, 417, 1223, 1584, 2864, 5640, 23653,
42749, 78553, 143591, 377556, 720327, 1569318, 3367130, 7309616,
14383312, 32139368, 58671803}, Joined -> True, AspectRatio -> 1/4,
Frame -> True, Mesh -> True,
MeshStyle ->
Directive[{Hue[0.07, 0.9500000000000001, 0.99], PointSize[.01]}],
PlotTheme -> "Detailed",
PlotStyle -> Directive[{Thickness[.004], Hue[0.1, 1, 0.99]}]]
Следует отметить, что можно добиться приемлемого результата для блоков одной длины, но потом потерпеть неудачу для блоков большего размера. Например, упомянутая выше последовательность Туэ–Морса имеет равные частоты Нулей и Единиц, но пары не встречаются с одинаковыми частотами, а тройки идентичных элементов просто никогда не встречаются.
В традиционной математике — и в частности в теории динамических систем — один из подходов состоит в том, чтобы рассмотреть не просто эволюцию из начального условия, состоящего из одной ячейки, а эволюцию из всех возможных начальных условий и в этом случае просто показать, что если шаблон развивается с равной вероятностью из всех возможных начальных условий, то столбцы ячеек, сгенерированные по Правилу 30, действительно будут содержать каждый блок с одинаковой частотой, но если задать одно и то же для разных распределений начальных условий, то на выходе получатся разные результаты, и не ясно, каков смысл этого вида анализа для конкретного случая одноклеточного начального условия.
Если бы в центральном столбце Правила 30 возникали разные блоки с разными частотами, то это сразу показывало бы, что центральный столбец «не случайный», или, другими словами, он имеет статистические закономерности, которые можно было бы использовать, по крайней мере, для статистического прогнозирования. Конечно, центральный столбец в принципе «предсказуем»: нам просто нужно запустить алгоритм Правила 30, чтобы вычислить его, но вопрос в том, существует ли здесь метод, с учетом только значений в центральном столбце, самостоятельно спрогнозировать или ужать их, скажем, с гораздо меньшими вычислительными затратами, чем генерация произвольного числа шагов во всем шаблоне Правила 30.
Представим запуск различных алгоритмов сжатия данных или статистического анализа и зададим себе вопрос о том, удастся ли этим алгоритмам найти закономерности в последовательности. И особенно когда мы начинаем размышлять об общих вычислительных возможностях Правила 30, можно предположить, что можно что-то доказать о том, как во всем спектре возможных алгоритмов анализа существует предел тому, насколько они могут сократить требуемые вычислительные мощности, связанные с эволюцией Пра

