[Из песочницы] Устойчивость обучения GAN
Впервые идея GAN была опубликована Яном Гудфеллоу Generative Adversarial Nets, Goodfellow et alб 2014, после этого GAN’ы являются одними из лучших генеративнх моделей.
Как и у любой другой генеративной модели задача GAN построить модель данных, а если более конкретно научиться генерировать семплы из распределения максимально близкого к распределению данных (обычно имеется датасет ограниченного размера, распределение данных в котором мы хотим промоделировать).
GAN«ы огромным количеством достоинств, но у них есть один существенный недостаток — их очень сложно обучать.
В последнее время вышел ряд работ посвященных устойчивости GAN:
Вдохновившись их идеями, я сделал небольшое свое исследование.
Я пытался сделать текст максимально простым и по-возможности использовать только простейшую математику. К сожалению, для того чтобы обосновать почему мы можем рассматривать свойства 2-х мерных векторных полей, приходится немножко копнуть в сторону вариационного исчисления. Но если кому-то эти термины не знакомы — можете смело переходить сразу к рассмотрению 2-х мерных векторных полей для разных типов GAN.
Мы попробуем сейчас заглянуть под капот процедуры обучения и понять чтоже там происходит.
GAN, основная проблема
GAN’ы состоят из двух нейронных сетей: дискриминатора и генератора. Генератор — позволяет семплировать из некоторого распределения (обычно его называют распределением генератора). Дискриминатор получает на вход семплы из оригинального датасета и генератора и учится предсказывать откуда этот семпл (датасет или генератор).
Схема GAN:
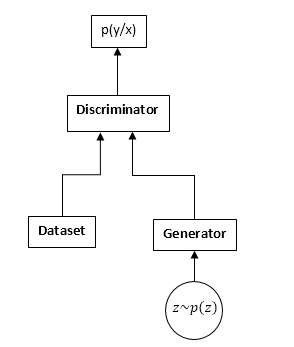
Процесс обучения GAN выглядит следующим образом:
- Берется n семплов из датасета и m семплов от генератора.
- Фиксируем веса генератора и делаем апдейт параметрам дискриминатора. Это обычная задача классификации. Только необходимости тренировать дискриминатор до сходимости у нас нет. А даже больше зачастую это еще и мешает.
- Фиксируем веса дискриминатора и делаем апдейт весам генератора, так чтобы дискриминатор начинал думать что наши семплы из датасета, а не от генератора.
- Повторяем 1–3, пока дискриминатор и генератор не придут в равновесие (т.е ни один ни другой не может «обмануть» другого).
Мы не будем рассматривать детально процесс обучения GAN. В интернете, да и на хабре в частности, имеется множество статей объясняющих этот процесс в деталях.
Нас будет интересовать совсем другое. А именно, из-за того что у нас идет соревнование двух нейронных сетей, задача перестает быть поиском минимума (максимума), а превращается в частных случаях в поиск седловой точки (т.е на 2 и 3 шаге мы один и тот же функционал пытаемся максимизировать по параметрам дискриминатора и минимизировать по параметрам генератора), а в более общих на 2 и 3 шаге мы можем оптимизировать абсолютно разные функционалы. Очевидно что задача минимакса это частный случай оптимизации разных функционалов — один функционал берется с разными знаками.
Давайте посмотрим на это в формулах. Будем считать что pd (x) — распределение откуда семплирован датасет, pg (x) — это распределение генератора, D (x) — выход с дискриминатора.
При обучении дискриминатора мы зачастую максимизируем такой функционал:
Вектор градиентов:
При обучении генератора мы максимизируем:
Вектор градиентов при этом:
В дальнейшем мы увидим что можно функционалы заменить соответственно на:
Где выбираются по определенным правилам. Кстати Ян Гудфеллоу в своей оригинальной статье использует
как при обучении обычного дискриминатора, а
выбирает таким чтобы улучшить градиенты на начальном этапе обучения:
На первый взгляд казалось бы задача очень похожа на обычную задачу обучения градиентным спуском (подъемом). Почему же тогда все кто сталкивался с обучением GAN«ов сходятся в том что это чертовски трудно?
Ответ кроется в структуре векторного поля, которое мы используем для обновления параметров нейронных сетей. В случае обычной задачи классификации мы используем только вектор градиентов, т.е поле является потенциальным (собственно оптимизируемый функционал является потенциалом этого векторного поля). А потенциальные векторные поля обладают некоторыми замечательными свойствами, одним из которых является отсутствие замкнутых кривых. Т.е в этом поле невозможно ходить кругами. А вот при обучении GAN несмотря на то что векторные поля для генератора и дискриминатора по отдельности являются потенциальными (это же градиетны), суммарное векторное поле не будет потенциальным. А это означает, что в этом поле могут быть замкнутые кривые, т.е мы можем ходить кругами. А это очень и очень плохо.
Возникает вопрос почему же все таки нам удается достаточно успешно обучать GAN, может поле таки безвихревое (потенциальное)? А если это так, то почему это так сложно?
Забегу вперед, поле к сожалению не является потенциальным, но оно обладает рядом хороших свойств. К сожалению, поле так же очень чувствительно к параметризации нейронных сетей (выбору функций активации, использованию DropOut, BatchNormalization и т.д.). Но обо всем по-порядку.
«Градиентное» поле GAN
Мы будем рассматривать функционалы обучения GAN в самом общем виде:
Нам необходимо оптимизировать оба функционала одновременно. Если предположить что D (x) и pg (x) абсолютно гибкие функции, т.е. мы можем в любой точке брать любое число, независимо от других точек. То известный факт из вариационного исчисления — изменять функцию нужно в напралении вариационной производной этого функционала (в общем-то полный аналог градиентного подъема).
Выпишем вариационную производную:
Мы будем рассматривать только первый фукнционал (для дискриминатора), для второго будет все тоже самое.
Но учитывая что на самом деле функцию мы можем менять только в множестве функций которые предствимы нашей нейронной сетью мы запишем:
$$display$$∆D (x) = \frac{\partial D (x)}{\partial θ_j}∆θ_j$$display$$
изменения параметров сети, в общем то обычный градиентный спуск (подъем):
$$display$$∆θj=\frac{\partial J}{\partial θ_j}μ$$display$$
µ — скорость обучения. Ну и производная по параметрам сети:
А теперь собираем все вместе:
Где:
Я раньше не встречал этой функции в литературе по машинному обучению, поэтому назову ее параметрическим ядром системы.
Ну или если перейти к непрерывным шагам по времи (от разностных уравнений к дифференциальным) получим:
Это уравнение показывает внутреннюю связь оригинального поля (поточечного для дискриминатора) и параметризации нейронной сети. Полностью аналогичное уравнение мы получим для генератора.
Учитывая что K (x, y) (параметрическое ядро) это положительно определенная функция (ну, а как же ведь она представима в виде скалярного произведения градиентов в соответсвующих точках), можно сделать вывод что любые изменения обучаемых функций (дискриминатора и генератора) принадлежат гильбертову пространству порожденному ядром, т.е. K (x, y). Интересно можно ли здесь получить какие нибудь содержательные результаты? Но мы в ту сторону смотреть пока не будем, а посмотрим в другую.
Как видно устойчивость GAN определяется двумя составляющими: вариационными производными функционалов и параметризацией нейронной сети. Наша задача посмотреть как ведет себя это поле поточечно, т.е в случае если наша сеть может представить абсолютно любую функцию. Задача превращается в анализ двумерного векторного поля. А это, я думаю, в наших силах.
Устойчивость
Итак, мы рассматриваем следующее векторное поле:
Очевидно что эти уравнения можно рассматривать всего лишь для одной точки х, с учетом того как выглядят наши вариационные производные:
Первое требование к этой системе уравнений — правые части должны обращаться в 0 когда:
Иначе мы будем пытаться обучать модель, которая заведомо не будет сходится к правильному решению. Т.е. D обязано быть решением следующего уравннеия:
Обозначим это решение как .
С учетом того что pg (x) плотность вероятности к правой части мы можем прибавить любое число не нарушая производных. Для того чтобы обеспечить 0 правой части в нужной точке вычтем значение в т. (это необходимо делать, если мы хотим рассматривать pg поточечно — переход от поля параметризованного плотностями вероятностей к свободным полям).
Как результат получаем следующее поле:
C этого момента будем изучать точки покоя и устойчивость полей именно такого вида.
Мы можем изучать два вида устойчивости: локальную (в окрестности точки покоя) и глобальную (используя метод функций Ляпунова).
Для изучения локальной устойчивости необходимо вычислить матрицу Якоби поля.
Для того чтобы поле было локально «устойчивым» необходимо чтобы собственные числа имели отрицательную действительную часть.
Различные виды GAN
-
Классический GAN
В классическом GAN мы используем обычный logloss:
Для обучения дискриминатора необходимо его максимизировать, для генератора — минимизировать. При этом поле будет выглядеть так:
Давайте посмотрим как будут эволюционировать параметры (pg и D) в этом поле. Для этого используем такой простой питоновский скрипт:Скриптdef get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = -np.log(1.-d) + np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show()
Для начальной точкиэто будет выглядеть так:

Точка покоя такого поля будет: pg = pd и D = 0.5
Можно легко проверить что действительные части собственных чисел матрицы Якоби отрицательны, т.е поле локально устойчиво.
Мы не будем заниматься доказательством глобальной устойчивости. Но если очень интересно можно поиграться с питоновским скриптом и убедиться что поле устойчиво для любых допустимых начальных значений. -
Модификация Яна Гудфеллоу
Мы уже обсуждали выше что Ян Гудфеллоу в оригинальной статье использовал немного модифицированную версию GAN. Для его версии функции были такими:
Поле же будет выглядеть так:
Питоновский скрипт будет тот же, только отлична функция поля:Скриптdef get_v(d, pg, pd): vd = pd/d - pg/(1.-d) vpg = np.log(d) - np.log(0.5) return vd, vpg d = 0.75 pg = 0.9 pd = 0.2 d_hist = [] pg_hist = [] lr = 1e-3 n_iter = 100000 for i in range(n_iter): d_hist.append(d) pg_hist.append(pg) vd, vpg = get_v(d, pg, pd) d = d + lr*vd pg = pg + lr*vpg plt.plot(d_hist, pg_hist, '-') plt.show()
И при тех же начальных данных картинка выглядит так: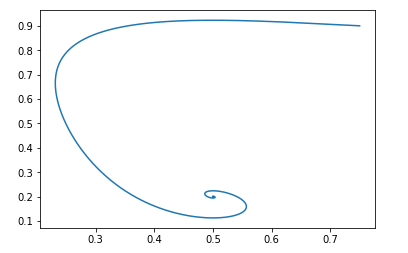
И опять же легко проверить что поле будет локально устойчивым.
Т.е с точки зрения сходимости такая модификация не ухудшает свойства GAN, зато имеет свои преимущества с точки зрения обучения нейронных сетей. -
Wasserstein GAN
Давайте посмотрим на еще один популярный вид GAN. Оптимизируемый функционал выглядит так:
Где D принадлежит классу 1-Липшицевых функций по х.
Мы хотим максимизировать его по D и минимизировать по pg.Очевидно что в этом случае:
И поле будет выглядеть так:
В этом поле легко угадывается окружность с центром в точке.
Т.е если мы пойдем по этому полю, то будем вечно ходить по кругу.Вот пример траектории в таком поле:
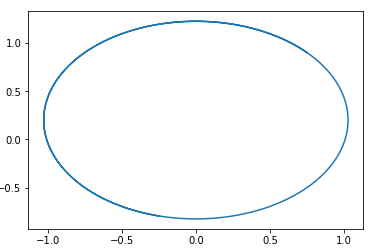
Возникает вопрос, почему же тогда получается обучать этот вид GAN? Ответ очень прост — в данном анализе не учитывается факт 1-Липшицевости D.Т. е мы не можем брать произвольные функции. Кстати это хорошо согласуется с результатами авторов… статьи. Для избежания хождения по кругу они рекомндуют тренировать дискриминатор до сходимости: Wasserstein GAN
-
Новые варианты GAN
Подбором функцийможно создавать различные варианты GAN. Главное требование к этим функциям это обеспечить наличие «правильной» точки покоя и устойчивость этой точки (желательно глобальную, но хотя бы локальную). Предоставляю читателю возможность самому вывести ограничения на функции f1, f2 и f3, необходимые для локальной устойчивости. Это несложно — достаточно рассмотреть квадратное уравнение для собственных чисел матрицы Якоби.
Приведу пример такого GAN:
Опять же предлагаю читателю самому построить поле этого GAN и доказать его устойчивость. (Кстати это одно из немногих полей для которого доказательтво глобальной устойчивости элементарно — достаточно выбрать функцию Ляпунова расстояние до точки покоя). Только нужно учесть что точка покоя D = 1.
Заключение и дальнейшие исследования
Из приведенного анализа видно что все классические GAN (за исключением Wassertein GAN, которая имеет свои способы улучшения стабильности) обладают «хорошими» полями. Т.е. следование этим полям имеет единственную точку покая в которой распределение генератора равно распределению данных.
Почему же тогда обучение GAN такая тяжелая задача. Ответ прост — параметризация нейронных сетей. При «плохой» параметризации мы можем так же пойти гулять кругами. Например в мои эксперименты показывают что, например, использование BatchNormalization в любой из сетей сразу превращает поле в замкнутое. А лучше всего работает Relu активация.
К сожалению на данный момент нет ни единого способа теоретически проверить какие элементы нейросети как меняют поле. Мне докажется переспективным исследовать свойства парметрического ядра системы — .
Хотелось еще рассказать про способы регуляризации полей GAN и взгляд с позиции двумерных полей на это. Рассмотреть алгоритмы Reinforcement Learning с этой позиции. И еще много чего. Но к сожалению, статья и так получилась слишком большой, так что об этом как нибудь в другой раз.
