Ранняя вселенная 3. Эффект Доплера и специальная теория относительности13.05.2018 11:36

На сайте бесплатных лекций MIT OpenCourseWare выложен курс лекций по космологии Алана Гуса, одного из создателей инфляционной модели вселенной.

Вашему вниманию предлагается перевод третьей лекции: «Инфляционная Космология 3. Эффект Доплера и специальная теория относительности».


Нерелятивистское доплеровское смещение

В конце прошлой лекции мы начали обсуждать доплеровское смещение и ввели обозначения. Речь шла о случае, когда наблюдатель неподвижен, а источник движется со скоростью $v$. Мы рассматривали звуковые волны, которые имели фиксированную скорость относительно некоторой среды.

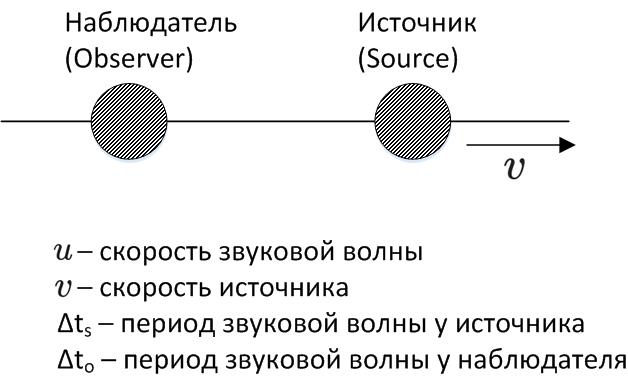
urquahdespbksmgiqppd3kemi_4.jpeg


Скорость волны относительно среды обозначим $u$, $v$ означает скорость удаления источнка, как показано на рисунке. $Δt_s$ — интервал времени между гребнями волны, испущенными источником, то есть период волны у источника. $Δt_o$ обозначает период волны у наблюдателя. Нам нужно вычислить связь между $Δt_o$ и $Δt_s$.

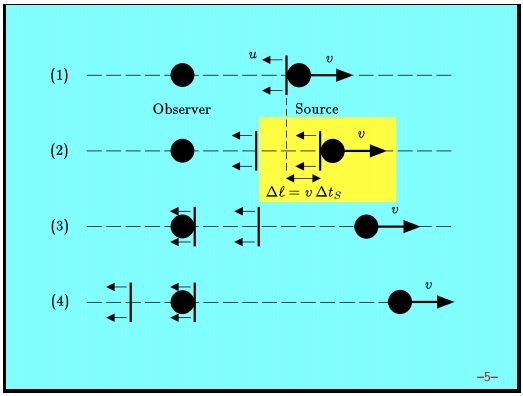
aztvxojwxheb_cw3c8bjhmfoi20.jpeg


На рисунке показаны различные этапы данного процесса. На первом этапе источник движется вправо и испускает первый гребень волны. Пока ничего особенно интересного.

На втором этапе источник испускает второй гребень волны. Но за это время источник переместился, это перемещение выделено желтым. Время между испусканием гребней волны равно $Δt_s$. Поэтому расстояние, которое пройдет источник в течение этого времени, равно $vΔt_s$. Назовем это расстояние $Δl$.
Это действительно важный этап, он объясняет доплеровское смещение. Видно, что второй гребень волны должен пройти немного больше чем первый гребень, на величину $Δl$.
Третий этап — волна прошла расстояние между наблюдателем и источником. На данном этапе первый гребень только что попал к наблюдателю. Четвертый этап — второй гребень попал к наблюдателю.

Чтобы понять, чему равно доплеровское смещение, нужно заметить, что, если бы оба объекта были неподвижны, то не было бы никакой разницы в периоде волны у наблюдателя и источника. Каждый гребень волны попадал бы к наблюдателю с некоторым запозданием, равным времени, за которое звуковая волна проходит расстояние от источника до наблюдателя. Но, в отсутствии движения, это запоздание одинаково для каждого гребня. Таким образом, если источник не движется $Δt_o$ = $Δt_s$.
Но из-за движения источника второму гребню придется пройти расстояние большее на величину $Δl$. Разница между периодами будет равна времени, которое потребуется волне, чтобы пройти это расстояние.

$Δt_o = Δt_s + \frac{Δl}u$


Мы знаем чему равно $Δl$. $Δl$ — это просто $vΔt_s$. Подставляя в наше уравнение получаем:

$Δt_o = Δt_s + \frac{vΔt_s}u$


Это уравнение показывает связь между $Δt_o$ и $Δt_s$. Можно найти отношение $Δt_o$ и $Δt_s$.

$\frac{Δt_o}{Δt_s} = 1+ \frac vu$


Это отношение является также отношением длины волны у наблюдателя $λ_o$ и у источника $λ_s$, поскольку длина волны просто равна скорости волны умноженной на ее период $Δt$.
Для описания доплеровского или красного смещения существует стандартное определение.

$$display$$\frac{λ_о}{λ_s} = 1 + z$$display$$


$z$ называется доплеровским или красным смещением. Астрономы вычитают единицу из отношения длин волн, чтобы в случае, когда оба объекта неподвижны, $z$ получилось равным 0. Такой случай соответствует отсутствию красного смещения и означает, что длина волны одна и та же у источника и у наблюдателя.

$$display$$\frac{λ_о}{λ_s} = \frac{Δt_o}{Δt_s} = 1+ \frac vu = 1 + z$$display$$


Таким образом, получаем красное смещение для нерелятивистского движения, или звуковой волны, в случае, когда движется источник:

$z = \frac vu $


Теперь перейдем к другому простому случаю, когда движется наблюдатель, а источник неподвижен. Источник у нас по-прежнему справа, а наблюдатель слева. Но на этот раз наблюдатель движется со скоростью $v$. В обоих случаях $v$ — это относительная скорость между источником и наблюдателем.

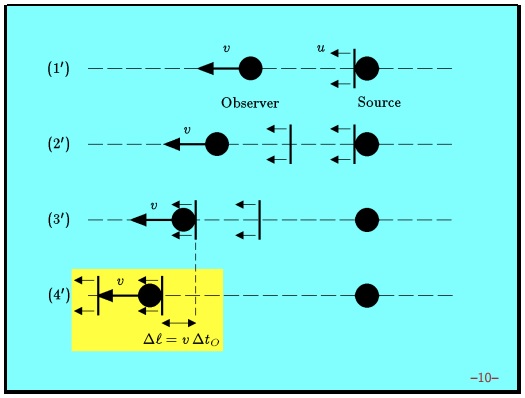
zl2c8ei9khgtxovtyzod5cp5n20.jpeg


Первый этап снова довольно прост. Источник излучает первый гребень волны. Этап номер два — второй гребень волны испускается источником. Этап номер три — первый гребень волны доходит до наблюдателя. Этап номер четыре — второй гребень волны доходит до наблюдателя.

Между временем, когда первый гребень приходит к наблюдателю, и временем, когда второй гребень приходит к наблюдателю, то есть временем между третьим и четвертым этапами наблюдатель переместился. Он переместился на расстояние равное $v$ умноженное на время между этими этапами. Время между этими этапами — это как раз время, которое проходит между получением двух гребней наблюдателем. Это то, что мы обозначили $Δt_o$ — период волны, измеренный наблюдателем. Пройденное расстояние — это просто $vΔt_o$. Все нужное для получения ответа происходит внутри желтого прямоугольника на последнем этапе.

Можно выписать уравнения для данного случая. В этот раз все немного сложнее. Начнем с той же идеи. $Δt_o$ был бы равен $Δt_s$, если бы не было движения. Но $Δt_o$ становится немного больше из-за дополнительного расстояния, которое проходит второй гребень. Это дополнительное расстояние снова назовем $Δl$. Время задержки снова будет $Δl$ деленное на $u$, скорость волны.

Но на этот раз у нас другая формула для $Δl$. На этот раз $Δl$ равна $vΔt_o$, а не $vΔt_s$, как было в предыдущем случае.

$$display$$Δt_o = Δt_s + \frac{Δl}u = Δt_s + \frac{vΔt_o}u$$display$$


Уравнение становится немного сложнее, потому что $Δt_o$ появляется с обеих сторон уравнения. Тем не менее, это уравнение с одним неизвестным, из него легко находится $Δt_o$. После несложных алгебраических преобразований получаем:

$\frac{Δt_o}{Δt_s} = (1-\frac vu)^{-1}$


Вычтя единицу получаем окончательное уравнение для $z$, вновь для нерелятивистского случая, когда движется наблюдатель:

$z = \frac{Δt_o}{Δt_s} -1 = (1-\frac vu)^{-1} - 1 = \frac {v/u}{1-v/u}$


Стоит отметить, что, когда скорость $v$ мала по сравнению со скоростью волны, что часто бывает если мы рассматриваем световую волну, но также встречается и в случае распространения звука, то обе формулы для $z$ почти одинаковы. Они обе пропорциональны $v/u$, если $v/u$ мало. Единственное различие — это знаменатель.

Во втором случае у нас знаменатель $1-v/u$. В первом случае $z$ просто равно $v/u$, и нет никакого знаменателя. Если $v/u$ мало, то знаменатель во втором случае близок к 1. Таким образом, две формулы будут почти одинаковыми. Можно описать это немного более точно, вычислив разницу между z в обоих случаях. Проделав несложные вычисления получаем:

$z_{источник\_движется} - z_{наблюдатель\_движется} = \frac {(v/u)^2}{1-\frac vu}$


Из формулы явно видно, что разница между $z$ пропорциональна $(v/u)^2$, а не просто $v/u$. Если $v/u$ равна одной тысячной, разница будет одна миллионная. Поэтому для медленных скоростей не имеет значения, движется ли источник или движется наблюдатель. Но ответы, конечно, будут сильно отличаться, если скорость $v$ сравнима с $u$.
СТУДЕНТ: Не нарушает ли это принцип относительности Галилея?

ПРЕПОДАВАТЕЛЬ: На самом деле нет. Для наших расчетов критически важным является воздух, в котором движется звуковая волна. В обоих случаях воздух покоится относительно рисунка. Если сделать преобразования Галилея от одной картины к другой, то после преобразования воздух будет двигаться, и получится не совсем та же картина.

Поэтому все согласуется с Галилеевской теорией относительности. Нужно помнить, что воздух здесь играет решающую роль. Когда мы говорим, что наблюдатель или источник находится в покое, в действительности имеется ввиду, что он находится в покое по отношению к среде, в которой движется волна.

СТУДЕНТ: Я заметил, что если $v$ больше $u$, то в первом случае ответ всегда положительный, все в порядке. Но если $v$ больше $u$ во втором случае, то получается отрицательный ответ. Мне кажется это странным.

ПРЕПОДАВАТЕЛЬ: Да, если $v$ больше $u$, то в случае движения наблюдателя ответ становится отрицательным. Это означает, что волна никогда не достигнет наблюдателя. Если наблюдатель движется быстрее чем скорость волны, волна никогда не догонит его. Поэтому получается такой необычный ответ. Если источник движется быстрее скорости волны, волна все равно достигает наблюдателя. Поэтому в первом случае мы получаем правильный ответ.

Релятивистское замедление времени
Давайте теперь перейдем к релятивистскому случаю. Нам потребуются некоторые факты из теории относительности. Поскольку существуют специализированные курсы по теории относительности, я не хочу, чтобы наши лекции стали таким курсом. Однако я хочу, чтобы наш курс был полностью понятен людям, не проходившим теорию относительности. Знание специальной теории относительности не является обязательным условием для нашего курса. Поэтому моей целью будет рассказать вам достаточно о специальной теории относительности, чтобы вы могли понимать дальнейшее. Я не буду выводить результаты, их вывод можно найти в других курсах. Если вы не хотите их посещать, то тоже ничего страшного. Но я хочу, чтобы мой курс был логически последовательным.

Итак, мы рассмотрим следствия специальной теории относительности, не пытаясь связать их непосредственно с основополагающими идеями специальной теории относительности. Однако я напомню, откуда взялась специальная теория относительности. Она зародилась в голове у Альберта Эйнштейна, когда он рассматривал Галилеевскую теорию относительности, о которой спрашивали минуту назад. Галилеевская теория относительности гласит, что если вы посмотрите на любой физический процесс в системе отсчета, которая движется с равномерной скоростью относительно другой системы отсчета, то в обоих системах отчета законы физики должны описываться одинаковым образом.

Теория относительности Галилея сыграла очень важную роль в истории физики. Ключевой вопрос во времена Галилея был — двигалась ли Земля вокруг Солнца или Солнце вокруг Земли. Галилей в этом споре принимал активное участие. Один из аргументов, доказывающих, что именно Солнце должно двигаться вокруг Земли, а не наоборот, был такой, что если Земля движется вокруг Солнца, то это означает, что мы движемся вместе с Землей с очень высокой скоростью. Скорость Земли вокруг Солнца высока по обычным меркам. Люди в то время считали, что очевидно, такое движение должно чувствоваться. Это было доказательство того, что Земля неподвижна, а Солнце движется. Потому что, в противном случае, чувствовался бы эффект быстрого движения Земли.

Для точки зрения Галилея, что движется именно Земля, критически важно, что мы такое движение не замечаем. Если мы движемся равномерно, то законы физики остаются точно такими же, какими они были бы, если бы мы оставались в покое. В этом суть теории относительности Галилея. Она была очень четко изложена Галилеем в его трудах.

Все это было справедливо для механических явлений. Однако в 1860-х годах Максвелл вывел свои уравнения. Вернее будет сказать, он завершил их вывод, большинство этих уравнений уже существовало. Из уравнений Максвелла следовало, что свет должен двигаться с фиксированной скоростью, которая может быть выражена через электрическую и магнитную постоянные $ε_0$ и $µ_0$. Эту скорость мы обозначаем $c$. Теперь представим, что вы попали на космический корабль, который движется со скоростью равной, скажем, половине $c$, и погнались за лучом света. Согласно физике, которая была известна в то время, получалось, что с точки зрения космического корабля, движущегося со скоростью $c/2$, световой импульс будет удаляться от него всего со скоростью $c/2$. Но это означает, что в системе отсчета такого быстро движущегося космического корабля законы физики должны каким-то образом отличаться. Уравнения Максвелла должны отличаться от стандартной формы.

Между физикой Максвелла и физикой Ньютона возникла некоторая напряженность. Напряженность, но не противоречие. Вполне возможно представить, что существует фиксированная система отсчета, в которой уравнения Максвелла имеют простую форму. Но уравнения Ньютона имеют одинаковую форму во всех инерциальных системах отсчета. Чтобы объяснить, почему так происходит, физики изобрели идею эфира, то есть среду, в которой распространяются световые волны, подобно воздуху, в котором распространяются звуковые волны. Система отсчета, в которой уравнения Максвелла имеют простую форму, является системой отсчета, в которой покоится эфир. Если мы движемся относительно эфира, то уравнения становятся другими. Именно так люди думали в 1904 году. Это была последовательная точка зрения, но это означало, что существует двойственность между электромагнетизмом и механикой.

Эйнштейн подумал, что может быть физика не такая нелогичная. Может быть, есть более элегантный способ, который может все объяснить. Он понял, что если модифицировать уравнения, которые используются для преобразования между разными системами отсчета, то можно сделать уравнения Максвелла инвариантными. Можно сделать так, чтобы уравнения Максвелла были действительны во всех системах отсчета. Давайте вернемся к нашему примеру с кораблем, гонящимся за световым лучом. Согласно новым уравнениям преобразования, которые предложил Эйнштейн, получается, хотя это сильно противоречит интуиции, что световой импульс удаляется от корабля со скоростью $с$. Хотя корабль сам движется со скоростью $c/2$, пытаясь догнать световой импульс.

Не очевидно, как такое может быть. Но, оказывается, именно так все и происходит. В основном это была догадка Эйнштейна. Он предположил, что эфира нет, что законы физики, и электромагнетизма, и механики одинаковы во всех системах отсчета. Для того, чтобы так получалось, уравнения преобразования между различными системами отсчета должны отличаться от тех, которые использовал Галилей.

Эти преобразования называются преобразованиями Лоренца. В этой лекции мы не будем их выписывать. В этой лекции мы поговорим о трех физических эффектах, которые следуют из преобразований Лоренца. Один из таких эффектов — это замедление времени. Немного позже мы обсудим два других основных эффекта, которые необходимы для понимания специальной теории относительности и объяснения, как такое может быть, что скорость света одинакова для всех наблюдателей, даже для тех, которые движутся.

hr_vw7zku-2iq9tlwm4ytdxypaa.jpeg


Замедление времени заключается в том, что если наблюдать за движущимися часами, то движущиеся часы «выглядят» идущими медленнее. Замечу, что я поставил слово «выглядят» в кавычки. Мы вернемся к этому и обсудим подробно, что подразумевается под словом «выглядят». Тем не менее, движущиеся часы будут выглядеть в моей системе отсчета идущими всегда медленнее в абсолютно предсказуемое число раз. Это число является известным выражением в специальной теории относительности $γ$:

$γ = \frac 1{\sqrt{1-β^2}}$


где $β$ — это просто обозначение для $v/c$, скорость движения часов, деленная на скорость света. Если $v/c$ мало, то замедление времени тоже мало, $γ$ почти равна 1. Замедление времени в 1 раз означает, что время вообще не замедляется. Если $γ$ близка к 1, то эффект будет незначительным. Но движущиеся часы всегда будут идти медленнее.

Давайте теперь вернемся к слову «выглядят». Тут есть тонкость. В прошлом году на PBS вышел фильм из четырех частей «Ткань космоса» Брайана Грина. Он пытался проиллюстрировать замедление времени. Он показал человека, сидящего в кресле, и человека, идущему к нему и несущего часы над головой. Камера показала, что человек, сидящий в кресле, увидит, как часы при движении начинают идти медленнее. Это не верно. Это не то, что он на самом деле увидит. И это ключевая проблема слова «выглядят».

Когда мы говорим, что движущиеся часы идут медленнее, мы не имеем в виду, что наблюдатель действительно это видит. Сложность ситуации заключается в том, что когда вы смотрите на что-то, вы регистрируете световые импульсы, приходящие к вашим глазам в данный момент времени. Поскольку свет проходит путь за конечное время, это означает, что вы видите разные вещи в разное время. Например, если есть какой-то объект, скажем, лазерная указка, летящая ко мне, я увижу ее заднюю часть там, где она была в более раннее время, чем передняя часть. Потому что свету, который испускается задней частью, требуется большее время, чтобы достичь моего глаза, чем свету, испущенному передней частью указки.

Поэтому, когда объект приближается ко мне, я увижу разные его части в разные моменты времени. Это все усложняет. То, что я увижу, принимая во внимание специальную теорию относительности, довольно сложно. Это можно вычислить, но для этого нет простого выражения. Нужно шаг за шагом вычислять, что я увижу в каждый конкретный момент времени. Это абсолютно не похоже на простую картину.

Таким образом, утверждение, что часы идут медленнее в $γ$ раз, основано не на том, что на самом деле увидит наблюдатель. Оно основано на том, что увидит система отсчета, а не конкретный человек. Это в конечном итоге приводит к более простой картине. Систему отсчета можно представить как набор линеек, соединенных друг с другом, так, что они образуют координатную сетку, и набор часов, расположенных повсюду внутри этой сетки.

При этом все наблюдения производятся локально. То есть, если мы хотим измерить время в какой-то системе отсчета, мы не используем центральные часы, ожидая, пока световой импульс достигнет этих центральных часов. Вместо этого, система отсчета заполнена часами, которые были синхронизированы друг с другом с самого начала. Если мы хотим знать, в какое время произошло какое-то событие, мы смотрим на часы, расположенные рядом с ним. Эти часы показывают, когда произошло это событие.

Как правило, именно таким образом мы работаем с различными системами координат. Если мы хотим понять, что увидит конкретный наблюдатель, то картина усложняется. Мы должны принять во внимание скорость света. Только исключив время на распространение света и рассчитав, что будут показывать локальные часы, мы увидим замедление времени в простой форме, что движущиеся часы всегда идут медленнее.

В частности, в примере с человеком, сидящим в кресле, и часами, приближающимися к нему. Человек будет испытывать, то, что мы обсуждаем на данной лекции — доплеровское смещение. Поскольку часы приближаются к нему, он будет испытывать синее смещение, а не красное. Он увидит, что часы идут быстрее, а не медленнее, в точности противоположное тому, что было показано в телевизионной программе. Ему будет казаться, что часы идут быстрее из-за того, что каждый последующий световой импульс проходит меньшее расстояние, поскольку часы приближаются к наблюдателю. Этот эффект дает больший вклад, чем эффект замедления движущихся часов, если сравнивать их с неподвижными часами, находящимися непосредственно рядом.

СТУДЕНТ: Если часы очень быстро пролетают мимо нас, могли бы мы увидеть их замедление, когда они находятся строго перпендикулярно к нам?

ПРЕПОДОВАТЕЛЬ: Да, вы совершенно правы. Когда часы пролетают мимо наблюдателя и находятся строго напротив него, скорость часов в его системе отсчета оказывается перпендикулярна скорости фотонов, которые он видит. При этом он увидит чистый эффект замедления времени.

Хочу добавить, что я и еще несколько человек из MIT принимали участие в создании фильма Брайана Грина. Мы долго обсуждали этот вопрос с Брайаном Грином по электронной почте. Мы все говорили, что это неправильно. Однако Брайан Грин занял позицию, что это было сделано намеренно, что он пытался проиллюстрировать эффект замедления времени, без обсуждения доплеровского смещения. Поскольку он не хотел говорить о доплеровском смещении, он просто проигнорировал факт его существования. Мы все считали, что это неправильно с педагогической точки зрения. Но мы не смогли убедить в этом Брайана.

Релятивистское доплеровское смещение

Теперь мы снова вычислим доплеровский сдвиг, на этот раз учитывая, что движущиеся часы идут медленнее в $γ$ раз. Мы займемся релятивистским случаем, где волна — это световая волна. А скорости могут быть сопоставимы со скоростью света. На этот раз эффект замедления времени достаточно велик, чтобы принимать его во внимание.

На этот раз оба ответа должны получиться одинаковыми. Если ответы получатся разными, то получится, что наша картина мира неверна, противоречива. Не должно иметь значения, движется ли источник или движется наблюдатель. Раньше это имело значение, и мы объясняли это тем, что в процесс был вовлечен воздух. Если сделать преобразование, чтобы перейти от одного случая к другому, от случая, когда движется источник, к случаю, когда движется наблюдатель, воздух в разных случаях будет имеет разную скорость. В одном случае он будет неподвижен, в другом случае он будет двигаться. Поэтому мы не планировали получить один и тот же ответ.

Но теперь, когда мы переходим от случая, где движется источник, к случаю, где движется наблюдатель, то с другой скоростью должен двигаться эфир. Но основная аксиома специальной теории относительности заключается в том, что эфира нет, по крайней мере, нет физических эффектов, возникающих из-за эфира. Так что можно притвориться, что его не существует. Поэтому в специальной теории относительности мы должны получить один и тот же ответ, будь то движущийся источник или движущийся наблюдатель. Это на самом деле одна и та же ситуация, только рассматриваемая из разных систем отсчета. Специальная теория относительности утверждает, что не имеет значения, в какой системе отсчета мы делаем вычисления. Мы воспользуемся теми же рисунками, но на этот раз примем во внимание тот факт, что движущиеся часы идут медленнее в $γ$ раз.

l5fomomizyzn2h19skanhzqgkaa.jpeg


Для начала давайте подумаем, на каком этапе для нас важно замедление времени движущихся часов? На втором. Именно на этом этапе источник измеряет движущимися часами период между испусканием двух гребней волны. Можно просто представить, что источник испускает серию импульсов, где каждый импульс представляет собой гребень волны. Для меня это выглядит немного проще, потому что не нужно думать о синусоидальной волне, которую на самом деле создает источник.

Время между этими импульсами, измеренное часами источника — это то, что мы обозначили как $Δt_s$. Источник движется на нашей картине. Все вычисления мы будем производить в нашей системе отсчета. Это очень важно, так как преобразования между системами отсчета немного сложны в специальной теории относительности. Когда вы решаете какую-нибудь задачу, то очень важно выбрать систему отсчета, которую вы будете использовать для описания задачи, и придерживаться ее. Если что-либо изначально описано в другой системе отсчета, нужно понять, как это выглядит в вашей системе отсчета. Чтобы затем соотнести это с другими событиями, которые описываются в вашей системе отсчета.

Для нашей задачи нашей системой отсчета будет система отсчета картинки, система отсчета, которая находится в покое относительно наблюдателя. Можно также назвать ее системой отсчета наблюдателя. Относительно этой системы отсчета источник движется. Источник испускает последовательность импульсов. Можно представить, что источник — это просто часы. Любое явление, повторяющееся с регулярными интервалами — это часы. Таким образом, источник представляет собой движущиеся часы, которые идут медленнее в $γ$ раз.

В остальном ничего не меняется. У наблюдателя также имеются часы, которые он использует для измерения времени между гребнями. Но часы наблюдателя покоятся в нашей системе отсчета. Таким образом, нет замедления времени, связанного с часами наблюдателя, есть только замедление времени, связанное с часами источника. И снова, все важное изображено внутри желтого прямоугольника. Теперь нужно взглянуть на уравнения и посмотреть, как они изменятся.

В прошлый раз интервал времени, измеренный наблюдателем, был суммой двух членов. В качестве первого члена был $Δt_s$, это был бы единственный член, если бы источник покоился. Это также верно и в нашем случае. Но время у источника идет медленнее в $γ$ раз. То есть если не учитывать изменений в длине пути — эти изменения мы учтем в следующем члене — то период, измеряемый наблюдателем будет отличаться от периода, измеряемого источника в $γ$ раз. Но нужно выяснить, будет ли $γ$ стоять в числителе или знаменателе. Для этого может помочь мысленный пример.

Итак, часы источника идут медленнее. Допустим, мы говорим о временном интервале в одну секунду. Если часы источника идут медленнее, это означает, что у нас должно пройти больше времени, чтобы у источника прошла секунда. Допустим, что часы идут медленнее в два раза. Это означает, что у источника будет проходить только одна секунда каждые наши две секунды. Это означает, что период, который мы увидим, будет длиннее, чем $Δt_s$ в $γ$ раз. Таким образом, перед первым членом мы ставим множитель $γ$. Второй член по прежнему равен $Δl/u$.

$$display$$Δt_o = γΔt_s + \frac{Δl}u$$display$$


Но выражение для $Δl$ также меняется. $Δl$ — это временной интервал, который требуется световому импульсу для перемещения на дополнительное расстояние. Дополнительное расстояние пропорционально времени между импульсами. Это время меняется из-за замедления времени часов источника. Так что второй член также увеличивается в $γ$ раз.

$$display$$Δt_o = γΔt_s + \frac{Δl}u = γΔt_s + \frac{vγΔt_s}u = γ (1+\frac vu)Δt_s$$display$$


Таким образом, весь ответ увеличивается в $γ$ раз. Учитывая, что 

$γ = \sqrt{\frac 1{1-{(\frac vu)}^2}}$


и 

$1-{(\frac vu)}^2 = (1-\frac vu)(1+\frac vu)$


после алгебраических преобразований получаем

$$display$$Δt_o = \sqrt \frac {1+β}{1-β}Δt_s$$display$$


Итак, мы получили ответ, учитывающий специальную теорию относительности, в случае движения источника. При учете теории относительности наш ответ увеличился в $γ$ раз. Мы ожидаем, что ответ не будет зависеть от того, движется источник или наблюдатель, но, конечно, это нужно проверить при помощи вычислений.

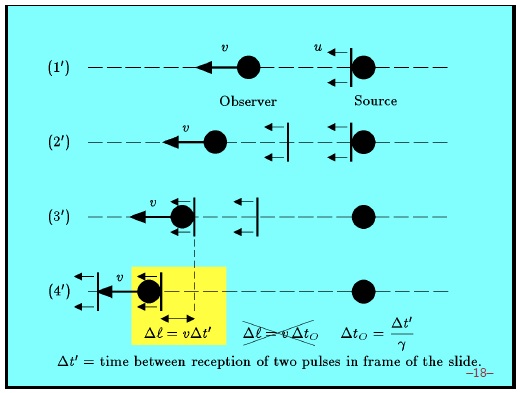
tmcxxfcm-pgmogp1p1hremmqbio.jpeg


За основу мы возьмем расчет, который мы уже сделали для нерелятивистского случая, с движущимся наблюдателем. Мы попробуем вычислить релятивистский случай. Теперь часы наблюдателя идут медленнее. Они идут медленнее относительно нас, относительно нашей системы отсчета, где наша система отсчета, по определению, система отсчета нашей картинки.

Самое важное опять происходит в желтом прямоугольнике. Источник неподвижен, поэтому $Δt_s$ — это просто период волны, измеренный нашими часами. Но период, измеренный наблюдателем, $Δt_o$, будет другим. Поэтому мы по-другому запишем наше уравнение, заменив выражение для $Δl$. Для $Δl$ вместо $vΔt_o$ мы запишем $vΔt'$.

$Δt'$ не равна © Geektimes