Открытый курс машинного обучения. Тема 8. Обучение на гигабайтах с Vowpal Wabbit17.04.2017 14:33

Всем привет!


96cffb939d3848ebb814641f0c8435f0.jpeg Вот мы постепенно и дошли до продвинутых методов машинного обучения, сегодня обсудим, как вообще подступиться к обучению модели, если данных гигабайты и десятки гигабайт. Обсудим приемы, позволяющие это делать: стохастический градиентный спуск (SGD) и хэширование признаков, посмотрим на примеры применения библиотеки Vowpal Wabbit. Домашнее задание будет как на реализацию SGD-алгоритмов, так и на обучение классификатора вопросов на StackOverflow по выборке в 10 Гб.


Поехали!



Список статей серии
  1. Первичный анализ данных с Pandas
  2. Визуальный анализ данных c Python
  3. Классификация, деревья решений и метод ближайших соседей
  4. Линейные модели классификации и регрессии
  5. Композиции: бэггинг, случайный лес. Кривые валидации и обучения
  6. Построение и отбор признаков
  7. Обучение без учителя: PCA, кластеризация
  8. Обучаемся на гигабайтах c Vowpal Wabbit
  9. Анализ временных рядов с помощью Python
  10. Градиентный бустинг

План
  • Стохастический градиентный спуск и онлайн-подход к обучению
    • Стохастический градиентный спуск
    • Онлайн-подход к обучению
  • Работа с категориальными признаками: Label Encoding, One-Hot Encoding, Hashing trick
    • Label Encoding
    • One-Hot Encoding
    • Хэширование признаков (Hashing trick)
  • Библиотека Vowpal Wabbit
    • Новости. Бинарная классификация
    • Новости. Многоклассовая классификация
    • Рецензии к фильмам IMDB
    • Классификация вопросов на StackOverflow
  • Домашнее задание
  • Полезные ссылки

Стохастический градиентный спуск и онлайн-подход к обучению

Стохастический градиентный спуск


Несмотря на то, что градиентный спуск — одна из первых тем, изучаемых в теории оптимизации и машинном обучении, сложно переоценить важность одной его модификации — стохастического градиентного спуска, который мы часто будем называть просто SGD (Stochastic Gradient Descent).


Напомним, что суть градиентного спуска — минимизировать функцию, делая небольшие шаги в сторону наискорейшего убывания функции. Название методу подарил тот факт из математического анализа, что вектор $\nabla f = (\frac{\partial f}{\partial x_1}, \ldots \frac{\partial f}{\partial x_n})^T$ частных производных функции $f(x) = f(x_1, \ldots x_n)$ задает направление наискорейшего возрастания этой функции. Значит, двигаясь в сторону антиградиента функции, можно уменьшать значения этой функции быстрее всего.


4f275da467a44fc4a8d1a11007776ed2.jpg


Это я в Шерегеше — всем катающим советую хотя бы раз в жизни там оказаться. Картинка для успокоения глаз, но с ее помощью можно пояснить интуицию градиентного спуска. Если задача — как можно быстрее спуститься с горы на сноуборде, то нужно в каждой точке выбирать максимальный уклон (если это совместимо с жизнью), то есть, вычислять антиградиент.


Пример — парная регрессия


Задачу простой парной регрессии можно решать с помощью градиентного спуска. Предположим, мы прогнозируем одну переменную по другой — рост по весу — и постулируем линейную зависимость роста от веса.


Код чтения данных и отрисовки диаграммы рассеяния
%matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns
import pandas as pd
data_demo = pd.read_csv('../../data/weights_heights.csv')

plt.scatter(data_demo['Weight'], data_demo['Height']);
plt.xlabel('Вес в фунтах')
plt.ylabel('Рост в дюймах');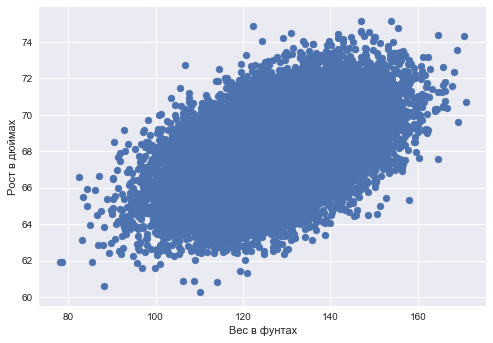

dce1634f214a4e8399cdddb08a2fee7d.png


Даны вектор $x$ длины $\ell$ — значения веса для каждого наблюдения (человека) и $y$ — вектор значений роста для каждого наблюдения (человека).


Задача: найти такие веса $w_0$ и $w_1$, чтобы при прогнозе роста по весу в виде $y_i = w_0 + w_1 x_i$ (где $y_i$ — $i$-ое значение роста, $x_i$ — $i$-ое значение веса) минимизировать квадратичную ошибку (можно и среднеквадратичную, но константа $\frac{1}{\ell}$ погоды не делает, а $\frac{1}{2}$ заведена для красоты):


$SE(w_0, w_1) = \frac{1}{2}\sum_{i=1}^\ell(y_i - (w_0 + w_1x_{i}))^2 \rightarrow min_{w_0,w_1}$


Делать мы это будем с помощью градиентного спуска, посчитав частные производные функции $SE(w_0, w_1)$ по весам в модели — $w_0$ и $w_1$. Итеративная процедура обучения будет задаваться простыми формулами обновления весов (меняем веса так, чтобы длать небольшой, пропорционально малой константе $\eta$, шаг в сторону антиградиента функции):


$\begin{array}{rcl} w_0^{(t+1)} = w_0^{(t)} -\eta \frac{\partial SE}{\partial w_0} |_{t} \\ w_1^{(t+1)} = w_1^{(t)} -\eta \frac{\partial SE}{\partial w_1} |_{t} \end{array}$


Если обратиться к ручке и бумажке и найти аналитические выражения для частных производных, то получим


$\begin{array}{rcl} w_0^{(t+1)} = w_0^{(t)} + \eta \sum_{i=1}^{\ell}(y_i - w_0^{(t)} - w_1^{(t)}x_i) \\ w_1^{(t+1)} = w_1^{(t)} + \eta \sum_{i=1}^{\ell}(y_i - w_0^{(t)} - w_1^{(t)}x_i)x_i \end{array}$


И все это довольно хорошо работает (в этой статье мы не будем обсуждать проблемы локальных минимумов, подбора шага градиентного спуска, момент и т.д. — про это и так много написано, можно обратиться к главе «Numeric Computation» книги «Deep Learning») пока данных не становится слишком много. Проблема такого подхода в том, что вычисление градиента сводится к суммированию некоторых величин для каждого объекта обучающей выборки. То есть попросту, проблема в том, что итераций алгоритму на практике требуется много, а на каждой итерации веса пересчитываются по формуле, в которой есть сумма по всей выборке вида $\sum_{i=1}^\ell$. А что если объектов в выборке миллионы и миллиарды?


ed185cf849cb4997b29fbb54fcd48bf9.jpg

Суть стохастического градиентного спуска — неформально, выкинуть знак суммы из формул пересчета весов и обновлять их по одному объекту. То есть в нашем случае


$\begin{array}{rcl} w_0^{(t+1)} = w_0^{(t)} + \eta (y_i - w_0^{(t)} - w_1^{(t)}x_i) \\ w_1^{(t+1)} = w_1^{(t)} + \eta (y_i - w_0^{(t)} - w_1^{(t)}x_i)x_i \end{array}$


При таком подходе на каждой итерации уже совсем не гарантировано движение в сторону наискорейшего убывания функции, и итераций может понадобиться на пару порядков больше, чем при обычном градиентном спуске. Зато пересчет весов на каждой итерации делается почти мгновенно.


В качестве иллюстрации возьмем картинку Эндрю Ына из его курса машинного обучения.


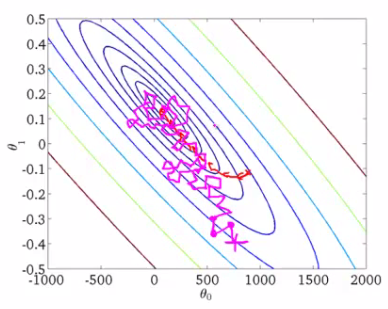
f8d90cf83b044255bb07df3373f25fc7.png

Нарисованы линии уровня некоторой функции, минимум который мы ищем. Красная кривая изображает изменение весов (на картинке $\theta_0$ и $\theta_1$ соответсвуют $w_0$ и $w_1$ в нашем примере). По свойствам градиента направление изменения в каждой точке будет перпендикулярно линиям уровня. При стохастическом подходе на каждой итерации веса меняется менее предсказуемо, порой даже кажется, что некоторые шаги неудачны — уводят от заветного минимума, но в итоге обе процедуры сходятся примерно к одному решению.


Сходимость стохатического градиентного спуска к тому же решению, что и у градиентного спуска, является одним из важнейших фактов, доказанных в теории оптимизации. Сейчас в эпоху Deep Data и Big Learning чаще даже градиентным спуском называет именно его стохастическую версию.


Онлайн-подход к обучению


Стохастический градиентный спуск, будучи одним из методов оптимизации, дает вполне практическое руководство к обучению алгоритмов классификации и регрессии на больших выборках — до сотен гигабайт (в зависимости от имеющейся памяти).


В случае парной регрессии, который мы рассмотрели, на диске можно хранить обучающую выборку $(X,y)$ и, не загружая ее в оперативную память (она может попросту не поместиться), считывать объекты по одному и обновлять веса:


$\begin{array}{rcl} w_0^{(t+1)} = w_0^{(t)} + \eta (y_i - w_0^{(t)} - w_1^{(t)}x_i) \\ w_1^{(t+1)} = w_1^{(t)} + \eta (y_i - w_0^{(t)} - w_1^{(t)}x_i)x_i \end{array}$


После обработки всех объектов обучающей выборки, функционал, который мы оптимизируем (квадратичная ошибка в задаче регрессии или, например, логистическая — в задаче классификации) снизится, но часто нужно несколько десятков проходов по выборке, чтобы он снизился достаточно.


Такой подход к обучению моделей часто называют онлайн-обучением, термин появился еще до того, как MOOC-и стали мэйнстримом.


fecfc5e6c6b34feeafe6f66cd1622aaa.jpg

В этой статье мы не рассматриваем многих нюансов стохастической оптимизации (вот хорошая статья на Хабре, фундаментально изучить эту тему можно по книге Boyd «Convex Optimization»), перейдем скорее к библиотеке Vowpal Wabbit, с помощью которой можно обучать простые модели на огромных выборках за счет стохастической оптимизации и еще одного трюка — хэширования признаков, о котором пойдет речь далее.


В библиотеке Scikit-learn классификаторы и регрессоры, обучаемые стохастическим градиентным спуском, реализованы классами SGDClassifier и SGDRegressor из sklearn.linear_model. Частью домашнего задания будет разобраться в них уже после собственной реализации этих простых онлайн-алгоритмов.


Работа с категориальными признаками: Label Encoding, One-Hot Encoding, Hashing trick

Label Encoding


Подавляющее большинство методов классификации и регрессии сформулированы в терминах евклидовых или метрических пространств, то есть подразумевают представление данных в виде вещественных векторов одинаковой размерности. В реальных данных, однако, не так редки категориальные признаки, принимающие дискретные значения, такие как да/нет или январь/февраль/…/декабрь. Обсудим то, как работать с такими данными, в частности с помощью линейных моделей, и что делать, если категориальных признаков много, да еще и у каждого куча уникальных значений.


Рассмотрим выборку UCI bank, в которой большая часть признаков — категориальные.


Код импорта библиотек и загрузки данных
import warnings
warnings.filterwarnings('ignore')
import os
import re
import numpy as np
import pandas as pd

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, accuracy_score
from sklearn.metrics import roc_auc_score, roc_curve, confusion_matrix
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.datasets import fetch_20newsgroups, load_files

import pandas as pd
from scipy.sparse import csr_matrix
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns

df = pd.read_csv('../../data/bank_train.csv')
labels = pd.read_csv('../../data/bank_train_target.csv', header=None)

df.head()

d8a8e85fc1c94e77ab3d30f6ea0f91d9.png

Нетрудно заметить, что достаточно много признаков в этом наборе данных не представлены числами. В таком виде данные еще нам не подходят — мы не сможем применять подавляющее большинство доступных нам методов.


Чтобы найти решение, давайте рассмотрим признак education:


Код построения графика
df['education'].value_counts().plot.barh();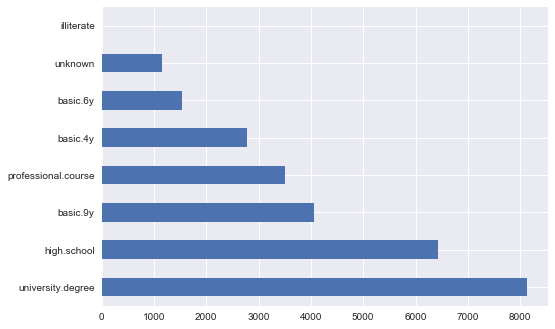

29a2c2e0ae7c4e159c24339660f67126.png

Естественным решением такой проблемы было бы однозначное отображение каждого значения в уникальное число. К примеру, мы могли бы преобразовать university.degree в 0, а basic.9y в 1. Эту простую операцию приходится делать часто, поэтому в модуле preprocessing библиотеки sklearn именно для этой задачи реализован класс LabelEncoder:


Метод fit этого класса находит все уникальные значения и строит таблицу для соответствия каждой категории некоторому числу, а метод transform непосредственно преобразует значения в числа. После fit у label_encoder будет доступно поле classes_, содержащее все уникальные значения. Можно их пронумеровать и убедиться, что преобразование выполнено верно.


Проверка преобразования LabelEncoder
label_encoder = LabelEncoder()

mapped_education = pd.Series(label_encoder.fit_transform(df['education']))
mapped_education.value_counts().plot.barh()
print(dict(enumerate(label_encoder.classes_)))

{0: 'basic.4y', 1: 'basic.6y', 2: 'basic.9y', 3: 'high.school', 4: 'illiterate', 5: 'professional.course', 6: 'university.degree', 7: 'unknown'}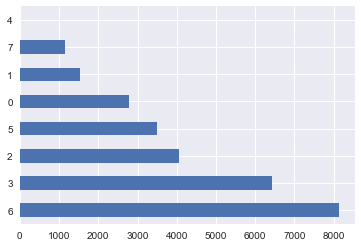

072fdff2ae834d5b86812f77dc131bac.png

Что произойдет, если у нас появятся данные с другими категориями? LabelEncoder ругнется, что не знает новую категорию.


Ругань LabelEncoder
try:
    label_encoder.transform(df['education'].replace('high.school', 'high_school'))
except Exception as e:
    print('Error:', e)

Error: y contains new labels: ['high_school']

Таким образом, при использовании этого подхода мы всегда должны быть уверены, что признак не может принимать неизвестных ранее значений. К этой проблеме мы вернемся чуть позже, а сейчас заменим весь столбец education на преобразованный:


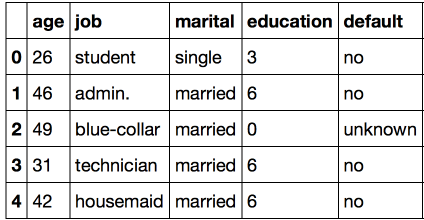
0c19847283ea4f5f87ed5fb477103416.png

Продолжим преобразование для всех столбцов, имеющих тип object — именно этот тип задается в pandas для таких данных.


Код
categorical_columns = df.columns[df.dtypes == 'object'].union(['education'])
for column in categorical_columns:
    df[column] = label_encoder.fit_transform(df[column])
df.head()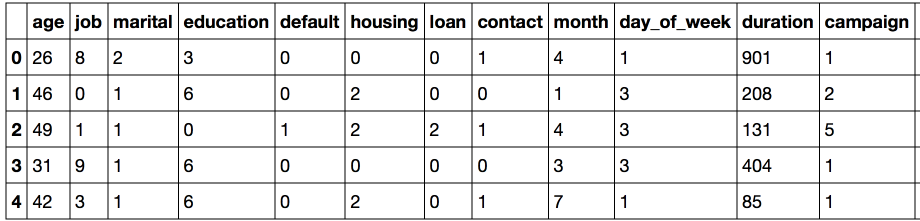

838d89538aa0418eb3638b06e0ed9eb8.png

Основная проблема такого представления заключается в том, что числовой код создал евклидово представление для данных.


К примеру, нами неявным образом была введена алгебра над значениями работы — мы можем вычесть работу клиента 1 из работы клиента 2. Конечно же, эта операция не имеет никакого смысла. Но именно на этом основаны метрики близости объектов, что делает бессмысленным применение метода ближайшего соседа на данных в таком виде. Аналогичным образом, никакого смысла не будет иметь применение линейных моделей. Посмотрим, как на таких данных сработает логистическая регрессия и убедимся, что ничего хорошего не получается.


Обучение логистической регресии
def logistic_regression_accuracy_on(dataframe, labels):
    features = dataframe.as_matrix()
    train_features, test_features, train_labels, test_labels = \
        train_test_split(features, labels)

    logit = LogisticRegression()
    logit.fit(train_features, train_labels)
    return classification_report(test_labels, logit.predict(test_features))

print(logistic_regression_accuracy_on(df[categorical_columns], labels))

             precision    recall  f1-score   support

          0       0.89      1.00      0.94      6159
          1       0.00      0.00      0.00       740

avg / total       0.80      0.89      0.84      6899

Для того, чтобы мы смогли применять линейные модели на таких данных, нам необходим другой метод, который называется One-Hot Encoding


One-Hot Encoding


Предположим, что некоторый признак может принимать 10 разных значений. В этом случае one hot encoding подразумевает создание 10 признаков, все из которых равны нулю за исключением одного. На позицию, соответствующую численному значению признака мы помещаем 1.


Эта техника реализована в sklearn.preprocessing в классе OneHotEncoder. По умолчанию OneHotEncoder преобразует данные в разреженную матрицу, чтобы не расходовать память на хранение многочисленных нулей. Однако в этом примере размер данных не является для нас проблемой, поэтому мы будем использовать «плотное» представление.


Код
onehot_encoder = OneHotEncoder(sparse=False)

encoded_categorical_columns = pd.DataFrame(onehot_encoder.fit_transform(df[categorical_columns]))
encoded_categorical_columns.head()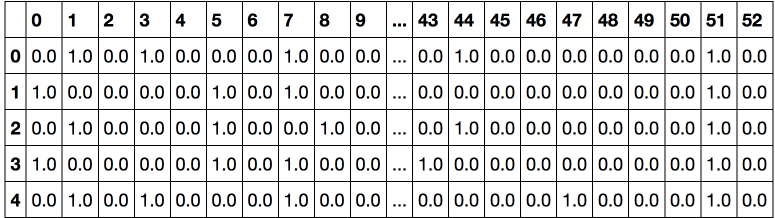

e76076a5978440ed80bec08ccd20e8e4.png

Мы получили 53 столбца — именно столько различных уникальных значений могут принимать категориальные столбцы исходной выборки. Преобразованные с помощью One-Hot Encoding данные начинают обретать смысл для линейной модели — точность по классу 1 (кто подтвердил кредит) составила 61%, полнота) — 17%.


Обучение логистической регресии
print(logistic_regression_accuracy_on(encoded_categorical_columns, labels))

             precision    recall  f1-score   support

          0       0.90      0.99      0.94      6126
          1       0.61      0.17      0.27       773

avg / total       0.87      0.89      0.87      6899

Хэширование признаков (Hashing trick)


Реальные данные могут оказаться гораздо более динамичными, и мы не всегда можем рассчитывать, что категориальные признаки не будут принимать новых значений. Все это сильно затрудняет использование уже обученных моделей на новых данных. Кроме того, LabelEncoder подразумевает предварительный анализ всей выборки и хранение построенных отображений в памяти, что затрудняет работу в режиме больших данных.


Для решения этих проблем существует более простой подход к векторизации категориальных признаков, основанный на хэшировании, известный как hashing trick.


Хэш-функции могут помочь нам в задаче поиска уникальных кодов для различных значений признака, к примеру: 


for s in ('university.degree', 'high.school', 'illiterate'):
    print(s, '->', hash(s))

university.degree -> -5073140156977989958
high.school -> -8439808450962279468
illiterate -> -2719819637717010547

Отрицательные и настолько большие по модулю значения нам не подойдут. Ограничим область значений хэш-функции: 


hash_space = 25
for s in ('university.degree', 'high.school', 'illiterate'):
    print(s, '->', hash(s) % hash_space)

university.degree -> 17
high.school -> 7
illiterate -> 3

Представим, что у нас в выборке есть холостой студент, которому позвонили в понедельник, тогда его вектор признаков будет сформирован аналогично One-Hot Encoding, но в едином пространстве фиксированного размера для всех признаков: 


hashing_example = pd.DataFrame([{i: 0.0 for i in range(hash_space)}])
for s in ('job=student', 'marital=single', 'day_of_week=mon'):
    print(s, '->', hash(s) % hash_space)
    hashing_example.loc[0, hash(s) % hash_space] = 1
hashing_example

job=student -> 6
marital=single -> 8
day_of_week=mon -> 16

Стоит обратить внимание, что в этом примере хэшировались не только значения признаков, а пары название признака + значение признака. Это необходимо, чтобы разделить одинаковые значения разных признаков между собой, к примеру: 


assert hash('no') == hash('no')
assert hash('housing=no') != hash('loan=no')

Может ли произойти коллизия хэш-функции, то есть совпадение кодов для двух разных значений? Нетрудно доказать, что при достаточном размере пространства хэширования это происходит редко, но даже в тех случаях, когда это происходит, это не будет приводить к существенному ухудшению качества классификации или регрессии.


32e2e8fbe012461b8791c26feb703edf.jpg

Возможно, вы спросите: «а что за хрень вообще происходит?», и покажется, что при хэшировании признаков страдает здравый смысл. Возможно, но эта эвристика — по сути, единственный подход к тому, чтобы работать с категориальными признаками, у которых много уникальных значений. Более того, эта техника себя хорошо зарекомендовала по результатами на практике. Подробней про хэширование признаков (learning to hash) можно почитать в этом обзоре, а также в материалах Евгения Соколова.


Библиотека Vowpal Wabbit

Vowpal Wabbit (VW) является одной из наиболее широко используемых библиотек в индустрии. Её отличает высокая скорость работы и поддержка большого количества различных режимов обучения. Особый интерес для больших и высокоразмерных данных представляет онлайн-обучение — самая сильная сторона библиотеки. Также реализовано хэширование признаков, и Vowpal Wabbit отлично подходит для работы с текстовыми данными.


Основным интерфейсом для работы с VW является shell. Vowpal Wabbit считывает данные из файла или стандартного ввода (stdin) в формате, который имеет следующий вид:


[Label] [Importance] [Tag]|Namespace Features |Namespace Features ... |Namespace Features


Namespace=String[:Value]


Features=(String[:Value] )*


где [] обозначает необязательные элементы, а (…)* означает повтор неопределенное число раз.


  • Label является числом, «правильным» ответом. В случае классификации обычно принимает значение 1/-1, а в случае регрессии некоторое вещественное число
  • Importance является числом и отвечает за вес примера при обучении. Это позволяет бороться с проблемой несбалансированных данных, изученной нами ранее
  • Tag является некоторой строкой без пробелов и отвечает за некоторое «название» примера, которое сохраняется при предсказании ответа. Для того, чтобы отделить Tag от Importance лучше начинать Tag с символа '.
  • Namespace служит для создания отдельных пространств признаков. В аргументах Namespace именуются по первой букве, это нужно учитывать при выборе их названий
  • Features являются непосредственно признаками объекта внутри Namespace. Признаки по умолчанию имеют вес 1.0, но его можно переопределить, к примеру feature:0.1.

К примеру, под такой формат подходит следующая строка: 


1 1.0 |Subject WHAT car is this |Organization University of Maryland:0.5 College Park

VW является прекрасным инструментом для работы с текстовыми данными. Убедимся в этом с помощью выборки 20newsgroups, содержащей новости из 20 различных тематических рассылок.


Новости. Бинарная классификация


newsgroups = fetch_20newsgroups('../../data/news_data')

Новости относится к одной из 20 тем: alt.atheism, comp.graphics, comp.os.ms-windows.misc, comp.sys.ibm.pc.hardware, comp.sys.mac.hardware, comp.windows.x, misc.forsalerec.autos, rec.motorcycles, rec.sport.baseball, rec.sport.hockey, sci.crypt, sci.electronics, sci.med, sci.space, soc.religion.christian, talk.politics.guns, talk.politics.mideast, talk.politics.misc, talk.religion.misc.


Рассмотрим первый текстовый документ этой коллекции:


Код
text = newsgroups['data'][0]
target = newsgroups['target_names'][newsgroups['target'][0]]

print('-----')
print(target)
print('-----')
print(text.strip())
print('----')

-----
rec.autos
-----
From: lerxst@wam.umd.edu (where's my thing)
Subject: WHAT car is this!?
Nntp-Posting-Host: rac3.wam.umd.edu
Organization: University of Maryland, College Park
Lines: 15

 I was wondering if anyone out there could enlighten me on this car I saw
the other day. It was a 2-door sports car, looked to be from the late 60s/
early 70s. It was called a Bricklin. The doors were really small. In addition,
the front bumper was separate from the rest of the body. This is 
all I know. If anyone can tellme a model name, engine specs, years
of production, where this car is made, history, or whatever info you
have on this funky looking car, please e-mail.

Thanks,
- IL
   ---- brought to you by your neighborhood Lerxst ----
----

Приведем данные к формату Vowpal Wabbit, при этом оставляя только слова не короче 3 символов. Здесь мы не выполняем многие важные в анализе текстов процедуры (стемминг и лемматизацию), но, как увидим, задача и так будет решаться хорошо.


Код
def to_vw_format(document, label=None):
    return str(label or '') + ' |text ' + ' '.join(re.findall('\w{3,}', document.lower())) + '\n'

to_vw_format(text, 1 if target == 'rec.autos' else -1)

'1 |text from lerxst wam umd edu where thing subject what car this nntp posting host rac3 wam umd edu organization university maryland college park lines was wondering anyone out there could enlighten this car saw the other day was door sports car looked from the late 60s early 70s was called bricklin the doors were really small addition the front bumper was separate from the rest the body this all know anyone can tellme model name engine specs years production where this car made history whatever info you have this funky looking car please mail thanks brought you your neighborhood lerxst\n'

Разобьем выборку на обучающую и тестовую и запишем в файл преобразованные таким образом документы. Будем считать документ положительным, если он относится к рассылке про автомобили rec.autos. Так мы построим модель, отличающую новости про автомобили от остальных.


Код
all_documents = newsgroups['data']
all_targets = [1 if newsgroups['target_names'][target] == 'rec.autos' 
               else -1 for target in newsgroups['target']]

train_documents, test_documents, train_labels, test_labels = \
    train_test_split(all_documents, all_targets, random_state=7)

with open('../../data/news_data/20news_train.vw', 'w') as vw_train_data:
    for text, target in zip(train_documents, train_labels):
        vw_train_data.write(to_vw_format(text, target))
with open('../../data/news_data/20news_test.vw', 'w') as vw_test_data:
    for text in test_documents:
        vw_test_data.write(to_vw_format(text))

Запустим Vowpal Wabbit на сформированном файле. Мы решаем задачу классификации, поэтому зададим функцию потерь в значение hinge (линейный SVM). Построенную модель мы сохраним в соответствующий файл 20news_model.vw.


!vw -d ../../data/news_data/20news_train.vw \
  --loss_function hinge -f ../../data/news_data/20news_model.vw

final_regressor = ../../data/news_data/20news_model.vw
Num weight bits = 18
learning rate = 0.5
initial_t = 0
power_t = 0.5
using no cache
Reading datafile = ../../data/news_data/20news_train.vw
num sources = 1
average  since         example        example  current  current  current
loss     last          counter         weight    label  predict features
1.000000 1.000000            1            1.0  -1.0000   0.0000      157
0.911276 0.822551            2            2.0  -1.0000  -0.1774      159
0.605793 0.300311            4            4.0  -1.0000  -0.3994       92
0.419594 0.233394            8            8.0  -1.0000  -0.8167      129
0.313998 0.208402           16           16.0  -1.0000  -0.6509      108
0.196014 0.078029           32           32.0  -1.0000  -1.0000      115
0.183158 0.170302           64           64.0  -1.0000  -0.7072      114
0.261046 0.338935          128          128.0   1.0000  -0.7900      110
0.262910 0.264774          256          256.0  -1.0000  -0.6425       44
0.216663 0.170415          512          512.0  -1.0000  -1.0000      160
0.176710 0.136757         1024         1024.0  -1.0000  -1.0000      194
0.134541 0.092371         2048         2048.0  -1.0000  -1.0000      438
0.104403 0.074266         4096         4096.0  -1.0000  -1.0000      644
0.081329 0.058255         8192         8192.0  -1.0000  -1.0000      174

finished run
number of examples per pass = 8485
passes used = 1
weighted example sum = 8485.000000
weighted label sum = -7555.000000
average loss = 0.079837
best constant = -1.000000
best constant's loss = 0.109605
total feature number = 2048932

Модель обучена. VW выводит достаточно много полезной информации по ходу обучения (тем не менее, ее можно погасить, если задать параметр --quiet). Подробно вывод диагностическйой информации разобран в документации VW на GitHub — тут. Обратите внимание, что average loss снижался по ходу выполнения итераций. Для вычисления функции потерь VW использует еще не просмотренные примеры, поэтому, как правило, эта оценка является корректной. Применим обученную модель на тестовой выборке, сохраняя предсказания в файл с помощью опции -p: 


!vw -i ../../data/news_data/20news_model.vw -t -d ../../data/news_data/20news_test.vw \
-p ../../data/news_data/20news_test_predictions.txt

only testing
predictions = ../../data/news_data/20news_test_predictions.txt
Num weight bits = 18
learning rate = 0.5
initial_t = 0
power_t = 0.5
using no cache
Reading datafile = ../../data/news_data/20news_test.vw
num sources = 1
average  since         example        example  current  current  current
loss     last          counter         weight    label  predict features
0.000000 0.000000            1            1.0  unknown   1.0000      349
0.000000 0.000000            2            2.0  unknown  -1.0000       50
0.000000 0.000000            4            4.0  unknown  -1.0000      251
0.000000 0.000000            8            8.0  unknown  -1.0000      237
0.000000 0.000000           16           16.0  unknown  -0.8978      106
0.000000 0.000000           32           32.0  unknown  -1.0000      964
0.000000 0.000000           64           64.0  unknown  -1.0000      261
0.000000 0.000000          128          128.0  unknown   0.4621       82
0.000000 0.000000          256          256.0  unknown  -1.0000      186
0.000000 0.000000          512          512.0  unknown  -1.0000      162
0.000000 0.000000         1024         1024.0  unknown  -1.0000      283
0.000000 0.000000         2048         2048.0  unknown  -1.0000      104

finished run
number of examples per pass = 2829
passes used = 1
weighted example sum = 2829.000000
weighted label sum = 0.000000
average loss = 0.000000
total feature number = 642215

Загрузим полученные предсказания, вычислим AUC и отобразим ROC-кривую:


Код
with open('../../data/news_data/20news_test_predictions.txt') as pred_file:
    test_prediction = [float(label) 
                             for label in pred_file.readlines()]

auc = roc_auc_score(test_labels, test_prediction)
roc_curve = roc_curve(test_labels, test_prediction)

with plt.xkcd():
    plt.plot(roc_curve[0], roc_curve[1]);
    plt.plot([0,1], [0,1])
    plt.xlabel('FPR'); plt.ylabel('TPR'); plt.title('test AUC = %f' % (auc)); plt.axis([-0.05,1.05,-0.05,1.05]);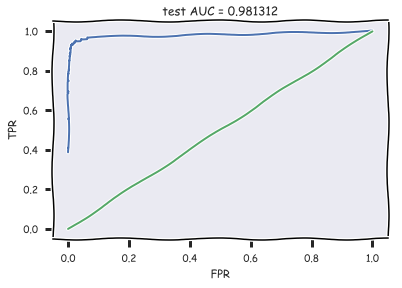

2e45a19788954d6eaee4c5a4c44272c2.png

Полученное значения AUC говорит о высоком качестве классификации.


Новости. Многоклассовая классификация

Используем ту же выборку, что в прошлой части, но решаем задачу многоклассовой классификации. Тут Vowpal Wabbit слегка капризничает — он любит, чтоб метки классов были распределены от 1 до K, где K — число классов в задаче классификации (в нашем случае — 20). Поэтому придется применить LabelEncoder, да еще и +1 потом добавить (LabelEncoder переводит метки в диапозон от 0 до K-1).


Код
all_documents = newsgroups['data']
topic_encoder = LabelEncoder()
all_targets_mult = topic_encoder.fit_transform(newsgroups['target']) + 1

Выборки будут те же, а метки поменяются, train_labels_mult и test_labels_mult — векторы меток от 1 до 20.


Код
train_documents, test_documents, train_labels_mult, test_labels_mult = \
    train_test_split(all_documents, all_targets_mult, random_state=7)

with open('../../data/news_data/20news_train_mult.vw', 'w') as vw_train_data:
    for text, target in zip(train_documents, train_labels_mult):
        vw_train_data.write(to_vw_format(text, target))
with open('../../data/news_data/20news_test_mult.vw', 'w') as vw_test_data:
    for text in test_documents:
        vw_test_data.write(to_vw_format(text))

Обучим Vowpal Wabbit в режиме многоклассовой классификации, передав параметр oaa (от «one against all»), равный числу классов. Также перечислим параметры, которые можно понастраивать, и от которых качество модели может довольно значительно зависеть (более полно — в официальном тьюториале по Vowpal Wabbit):


  • темп обучения (-l, по умолчанию 0.5) — коэффициент перед изменением весов модели при каждом изменении
  • степень убывания темпа обучения (--power_t, по умолчанию 0.5) — на практике проверено, что если темп обучения уменьшается при увеличении числа итераций стохастического градиентного спуска, то минимум функции находится лучше
  • функция потерь (--loss_function) — от нее, по сути, зависит обучаемый алгоритм. Про функции потерь в документации

  • регуляризация (-l1) — тут надо обратить внимание на то, что в VW регуляризация считается для каждого объекта, поэтому коэффициенты регуляризации обычно берутся малыми, около $10^{-20}.$


    Дополнительно можно попробовать автоматическую настройку параметров Vowpal Wabbit с Hyperopt. Пока это работает только с Python 2. Статья на Хабре.



Код
%%time
!vw --oaa 20 ../../data/news_data/20news_train_mult.vw \
-f ../../data/news_data/20news_model_mult.vw --loss_function=hinge

final_regressor = ../../data/news_data/20news_model_mult.vw
Num weight bits = 18
learning rate = 0.5
initial_t = 0
power_t = 0.5
using no cache
Reading datafile = ../../data/news_data/20news_train_mult.vw
num sources = 1
average  since         example        example  current  current  current
loss     last          counter         weight    label  predict features
1.000000 1.000000            1            1.0       15        1      157
1.000000 1.000000            2            2.0        2       15      159
1.000000 1.000000            4            4.0       15       10       92
1.000000 1.000000            8            8.0       16       15      129
1.000000 1.000000           16           16.0       13       12      108
0.937500 0.875000           32           32.0        2        9      115
0.906250 0.875000           64           64.0       16       16      114
0.867188 0.828125          128          128.0        8        4      110
0.816406 0.765625          256          256.0        7       15       44
0.646484 0.476562          512          512.0       13        9      160
0.502930 0.359375         1024         1024.0        3        4      194
0.388672 0.274414         2048         2048.0        1        1      438
0.300293 0.211914         4096         4096.0       11       11      644
0.225098 0.149902         8192         8192.0        5        5      174

finished run
number of examples per pass = 8485
passes used = 1
weighted example sum = 8485.000000
weighted label sum = 0.000000
average loss = 0.222392
total feature number = 2048932
CPU times: user 7.97 ms, sys: 13.9 ms, total: 21.9 ms
Wall time: 378 ms

%%time
!vw -i ../../data/news_data/20news_model_mult.vw -t \
-d ../../data/news_data/20news_test_mult.vw \
-p ../../data/news_data/20news_test_predictions_mult.txt

only testing
predictions = ../../data/news_data/20news_test_predictions_mult.txt
Num weight bits = 18
learning rate = 0.5
initial_t = 0
power_t = 0.5
using no cache
Reading datafile = ../../data/news_data/20news_test_mult.vw
num sources = 1
average  since         example        example  current  current  current
loss     last          counter         weight    label  predict features
1.000000 1.000000            1            1.0  unknown        8      349
1.000000 1.000000            2            2.0  unknown        6       50
1.000000 1.000000            4            4.0  unknown       18      251
1.000000 1.000000            8            8.0  unknown       18      237
1.000000 1.000000           16           16.0  unknown        4      106
1.000000 1.000000           32           32.0  unknown       15      964
1.000000 1.000000           64           64.0  unknown        4      261
1.000000 1.000000          128          128.0  unknown        8       82
1.000000 1.000000          256          256.0  unknown       10      186
1.000000 1.000000          512          512.0  unknown        1      162
1.000000 1.000000         1024         1024.0  unknown       11      283
1.000000 1.000000         2048         2048.0  unknown       14      104

finished run
number of examples per pass = 2829
passes used = 1
weighted example sum = 2829.000000
weighted label sum = 0.000000
average loss = 1.000000
total feature number = 642215
CPU times: user 4.28 ms, sys: 9.65 ms, total: 13.9 ms
Wall time: 166 ms

with open('../../data/news_data/20news_test_predictions_mult.txt') as pred_file:
    test_prediction_mult = [float(label) 
                            for label in pred_file.readlines()]

accuracy_score(test_labels_mult, test_prediction_mult)

Получаем долю правильных ответов около 87%.


В качестве примера анализа результатов, посмотрим, с какими темами классификатор путает атеизм.


Код
M = confusion_matrix(test_labels_mult, test_prediction_mult)
for i in np.where(M[0,:] > 0)[0][1:]:
    print(newsgroups['target_names'][i], M[0,i], )

rec.autos 1
rec.sport.baseball 1
sci.med 1
soc.religion.christian 3
talk.religion.misc 5

Эти темы: rec.autos, rec.sport.baseball, sci.med, soc.religion.christian и talk.religion.misc.


Рецензии к фильмам IMDB

В этой части мы будем заниматься бинарной классификацией отзывов к фильмам, публикованным на сайте IMDB. Обратите внимание, насколько быстро будет работать Vowpal Wabbit.


Используем функцию load_files из sklearn.datasets для загрузки отзывов по фильмам отсюда. Скачайте данные и укажите свой путь к каталогу imdb_reviews (в нем должны быть каталоги train и test). Разархивирование может занять несколько минут — там 100 тыс. файлов. В обучающей и тестовой выборках по 12500 тысяч хороших и плохих отзывов к фильмам. Отделим данные (собственно, тексты) от меток.


Код
# поменяйте на свой путь
path_to_movies = '/Users/y.kashnitsky/Yandex.Disk.localized/ML/data/imdb_reviews/'
reviews_train = load_files(os.path.join(path_to_movies, 'train'))
text_train, y_train = reviews_train.data, reviews_train.target

print("Number of documents in training data: %d" % len(text_train))
print(np.bincount(y_train))

Number of documents in training data: 25000
[12500 12500]

То же самое с тестовой выборкой.


reviews_test = load_files(os.path.join(path_to_movies, 'test'))
text_test, y_test = reviews_test.data, reviews_train.target
print("Number of documents in test data: %d" % len(text_test))
print(np.bincount(y_test))

Number of documents in test data: 25000
[12500 12500]

Примеры отзывов: 


"Zero Day leads you to think, even re-think why two boys/young men would do what they did - commit mutual suicide via slaughtering their classmates. It captures what must be beyond a bizarre mode of being for two humans who have decided to withdraw from common civility in order to define their own/mutual world via coupled destruction.

It is not a perfect movie but given what money/time the filmmaker and actors had - it is a remarkable product. In terms of explaining the motives and actions of the two young suicide/murderers it is better than 'Elephant' - in terms of being a film that gets under our 'rationalistic' skin it is a far, far better film than almost anything you are likely to see. 

Flawed but honest with a terrible honesty."

Это был хороший отзыв. А вот плохой: 


'Words can\'t describe how bad this movie is. I can\'t explain it by writing only. You have too see it for yourself to get at grip of how horrible a movie really can be. Not that I recommend you to do that. There are so many clich\xc3\xa9s, mistakes (and all other negative things you can imagine) here that will just make you cry. To start with the technical first, there are a LOT of mistakes regarding the airplane. I won\'t list them here, but just mention the coloring of the plane. They didn\'t even manage to show an airliner in the colors of a fictional airline, but instead used a 747 painted in the original Boeing livery. Very bad. The plot is stupid and has been done many times before, only much, much better. There are so many ridiculous moments here that i lost count of it really early. Also, I was on the bad guys\' side all the time in the movie, because the good guys were so stupid. "Executive Decision" should without a doubt be you\'re choice over this one, even the "Turbulence"-movies are better. In fact, every other movie in the world is better than this one.'

Будем использовать ранее написанную функцию to_vw_format. Подготовим обучающую (movie_reviews_train.vw), отложенную (movie_reviews_valid.vw) и тестовую (movie_reviews_test.vw) выборки для Vowpal Wabbit. 70% исходной обучаюшей выбо

© Habrahabr.ru