Методы оптимизации нейронных сетей04.01.2017 15:18

В подавляющем большинстве источников информации о нейронных сетях под «а теперь давайте обучим нашу сеть» понимается «скормим целевую функцию оптимизатору» лишь с минимальной настройкой скорости обучения. Иногда говорится, что обновлять веса сети можно не только стохастическим градиентным спуском, но безо всякого объяснения, чем же примечательны другие алгоритмы и что означают загадочные $\inline \beta$ и $\inline \gamma$ в их параметрах. Даже преподаватели на курсах машинного обучения зачастую не заостряют на этом внимание. Я бы хотел исправить недостаток информации в рунете о различных оптимизаторах, которые могут встретиться вам в современных пакетах машинного обучения. Надеюсь, моя статья будет полезна людям, которые хотят углубить своё понимание машинного обучения или даже изобрести что-то своё.

Под катом много картинок, в том числе анимированных gif.

Статья ориентирована на знакомого с нейронными сетями читателя. Предполагается, что вы уже понимаете суть backpropagation и SGD. Я не буду вдаваться в строгое доказательство сходимости представленных ниже алгоритмов, а наоборот, постараюсь донести их идеи простым языком и показать, что формулы открыты для дальнейших экспериментов. В статье перечислены далеко не все сложности машинного обучения и далеко не все способы их преодолевать.

Зачем нужны ухищрения

Напомню, как выглядят формулы для обычного градиентного спуска:

$(1)$

$\Delta \theta = -\eta \nabla_\theta J( \theta)$

$(2)$

$\theta = \theta + \Delta \theta = \theta - \eta \nabla_\theta J( \theta)$

где $\inline \theta$ — параметры сети, $\inline J( \theta)$ — целевая функция или функция потерь в случае машинного обучения, а $\inline \eta$ — скорость обучения. Выглядит удивительно просто, но много магии сокрыто в $\inline \nabla_\theta J( \theta)$ — обновить параметры выходного слоя довольно просто, но чтобы добраться до параметров слоёв за ним, приходится проходить через нелинейности, производные от которых вносят свой вклад. Это знакомый вам принцип обратного распространения ошибки — backpropagation.

Явно расписанные формулы для обновления весов где-нибдуь в середине сети выглядят страшненько, ведь каждый нейрон зависит ото всех нейронов, с которымии он связан, а те — ото всех нейронов, с которыми связаны они, и так далее. При этом даже в «игрушечных» нейронных сетях может быть порядка 10 слоёв, а среди сетей, удерживающих олимп классифицирования современных датасетов — намного, намного больше. Каждый вес — переменная в $\inline J( \theta)$ . Такое невероятное количество степеней свободы позволяет строить очень сложные отображения, но приносит исследователям головную боль:

Застревание в локальных минимумах или седловых точках, коих для функции от $\inline> 10^6$ переменных может быть очень много.
Сложный ландшафт целевой функции: плато чередуются с регионами сильной нелинейности. Производная на плато практически равна нулю, а внезапный обрыв, наоборот, может отправить нас слишком далеко.
Некоторые параметры обновляются значительно реже других, особенно когда в данных встречаются информативные, но редкие признаки, что плохо сказывается на нюансах обобщающего правила сети. С другой стороны, придание слишком большой значимости вообще всем редко встречающимся признакам может привести к переобучению.
Слишком маленькая скорость обучения заставляет алгоритм сходиться очень долго и застревать в локальных минимумах, слишком большая — «пролетать» узкие глобальные минимумы или вовсе расходиться

Вычислительной математике известны продвинутые алгоритмы второго порядка, которым под силу найти хороший минимум и на сложном ландшафте, но тут удар снова наносит количество весов. Чтобы воспользоваться честным методом второго порядка «в лоб», придётся посчитать гессиан $\inline J( \theta)$ — матрицу производных по каждой паре параметров пары параметров (уже плохо) — а, скажем, для метода Ньютона, ещё и обратную к ней. Приходится изобретать всяческие ухищрения, чтобы справиться с проблемами, оставляя задачу вычислительно подъёмной. Рабочие оптимизаторы второго порядка существуют, но пока что давайте сконцентрируемся на том, что мы можем достигнуть, не рассматривая вторые производные.

Nesterov Accelerated Gradient

Сама по себе идея методов с накоплением импульса до очевидности проста: «Если мы некоторое время движемся в определённом направлении, то, вероятно, нам следует туда двигаться некоторое время и в будущем». Для этого нужно уметь обращаться к недавней истории изменений каждого параметра. Можно хранить последние $\inline n$ экземпляров $\inline \Delta \theta$ и на каждом шаге по-честному считать среднее, но такой подход занимает слишком много памяти для больших $\inline n$ . К счастью, нам и не нужно точное среднее, а лишь оценку, поэтому воспользуемся экспоненциальным скользящим средним.

$(3)$

$v_t = \gamma v_{t-1} + (1-\gamma) x$

Чтобы накопить что-нибудь, будем умножать уже накопленное значение на коэффициент сохранения $\inline 0 < \gamma < 1$ и прибавлять очередную величину, умноженную на $\inline 1-\gamma$ . Чем ближе $\inline \gamma$ к единице, тем больше окно накопления и сильнее сглаживание — история $\inline x$ начинает влиять сильнее, чем каждое очередное $\inline x$ . Если $\inline x=0$ c какого-то момента, $\inline v_t$ затухают по геометрической прогрессии, экспоненциально, отсюда и название. Применим экспоненциальное бегущее среднее, чтобы накапливать градиент целевой функции нашей сети:

$(4)$

$v_t = \gamma v_{t-1} + \eta \nabla_\theta J( \theta)$

$(5)$

$\theta = \theta - v_t$

Где $\inline \gamma$ обычно берётся порядка $\inline 0.9$ . Обратите внимание, что $\inline 1-\gamma$ не пропало, а включилось в $\inline \eta$ ; иногда можно встретить и вариант формулы с явным множителем. Чем меньше $\inline \gamma$ , тем больше алгоритм ведёт себя как обычный SGD. Чтобы получить популярную физическую интерпретацию уравнений, представьте как шарик катится по холмистой поверхности. Если в момент $\inline t$ под шариком был ненулевой уклон ( $\inline \nabla_\theta J( \theta)$ ), а затем он попал на плато, он всё равно продолжит катиться по этому плато. Более того, шарик продолжит двигаться пару обновлений в ту же сторону, даже если уклон изменился на противоположный. Тем не менее, на шарик действует вязкое трение и каждую секунду он теряет $\inline 1-\gamma$ своей скорости. Вот как выглядит накопленный импульс для разных $\inline \gamma$ (здесь и далее по оси X отложены эпохи, а по Y — значение градиента и накопленные значения):

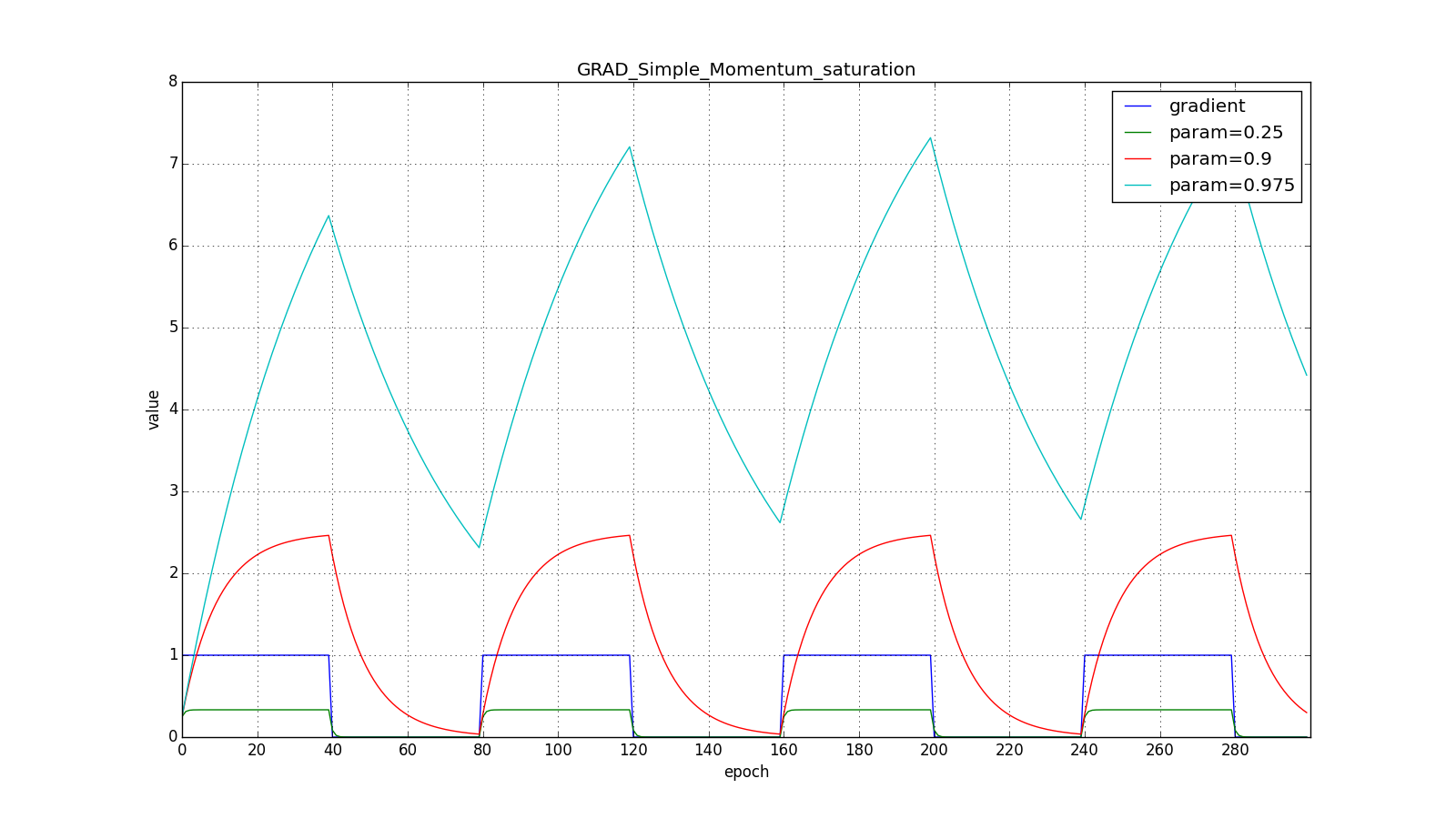
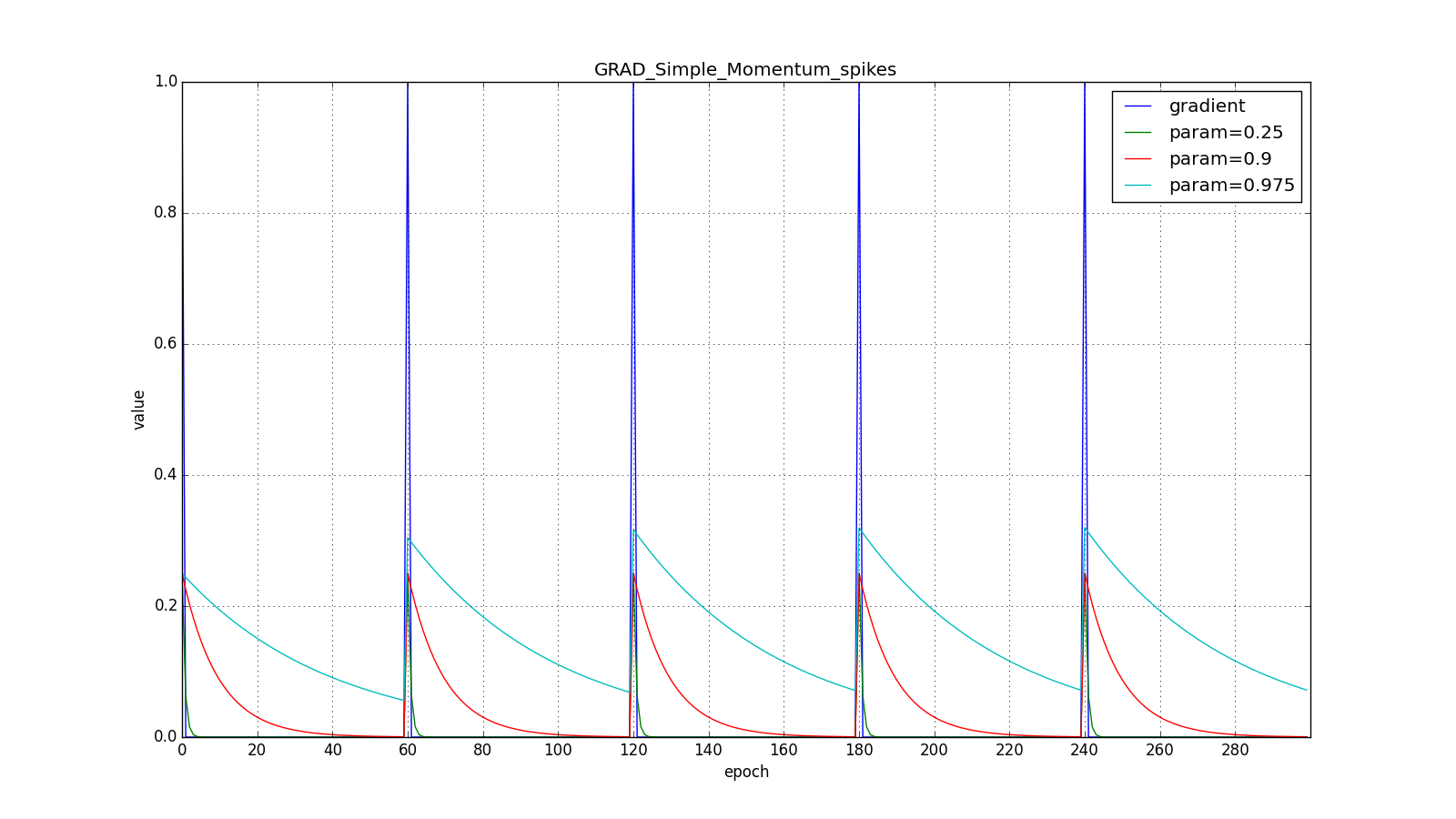
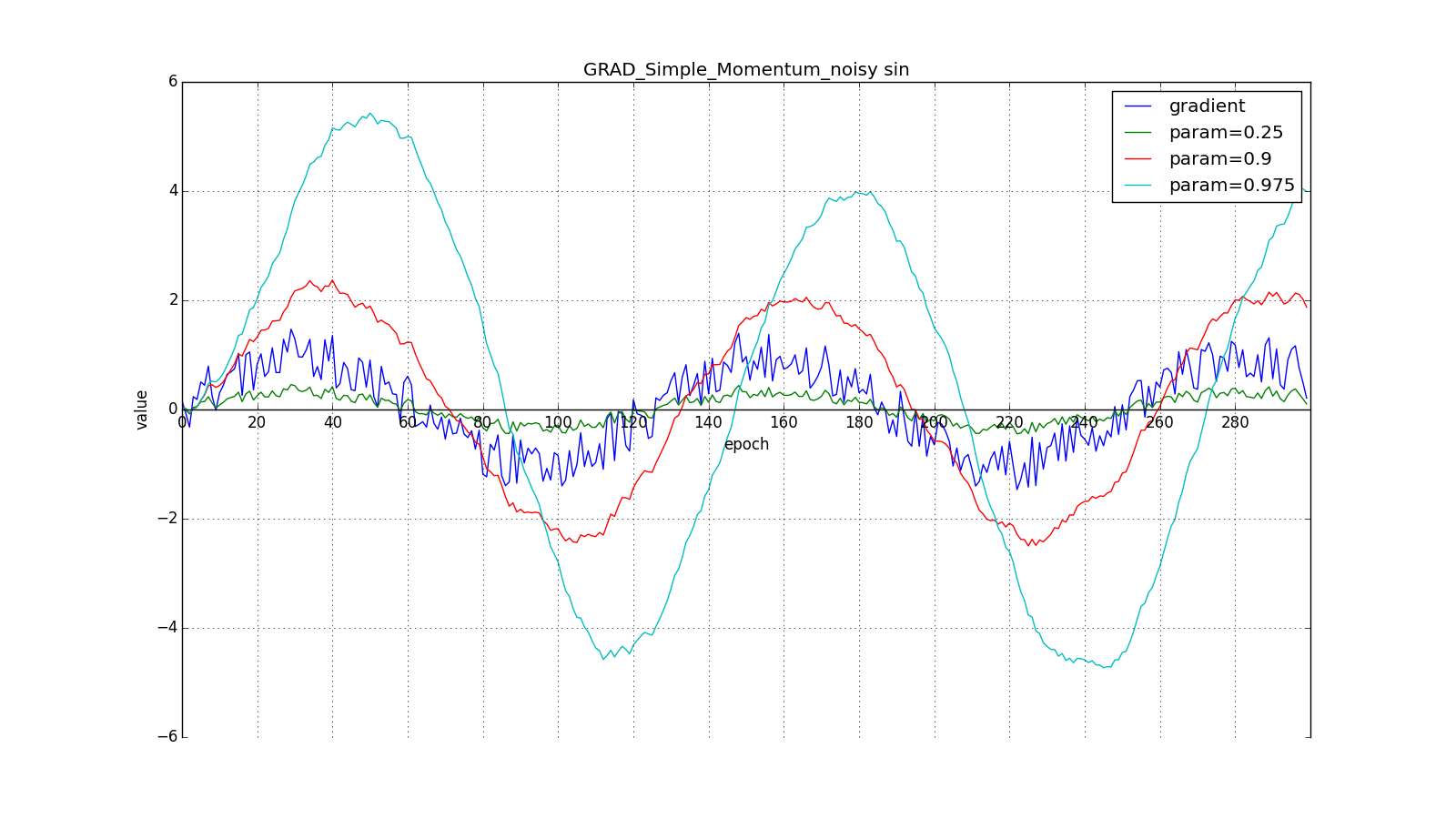
Заметьте, что накопленное в $\inline v_t$ значение может очень сильно превышать значение каждого из $\inline \eta \nabla_\theta J( \theta)$ . Простое накопление импульса уже даёт хороший результат, но Нестеров идёт дальше и применяет хорошо известную в вычислительной математике идею: заглядывание вперёд по вектору обновления. Раз уж мы всё равно собираемся сместиться на $\inline \gamma v_{t-1}$ , то давайте посчитаем градиент функции потерь не в точке $\inline \theta$ , а в $\inline \theta - \gamma v_{t-1}$ . Отсюда:

$(6)$

$v_t = \gamma v_{t-1} + \eta \nabla_\theta J( \theta - \gamma v_{t-1} )$

$(7)$

$\theta = \theta - v_t$

Такое изменение позволяет быстрее «катиться», если в стороне, куда мы направляемся, производная увеличивается, и медленнее, если наоборот. Особенно этого хорошо видно для $\inline \gamma=0.975$ для графика с синусом.

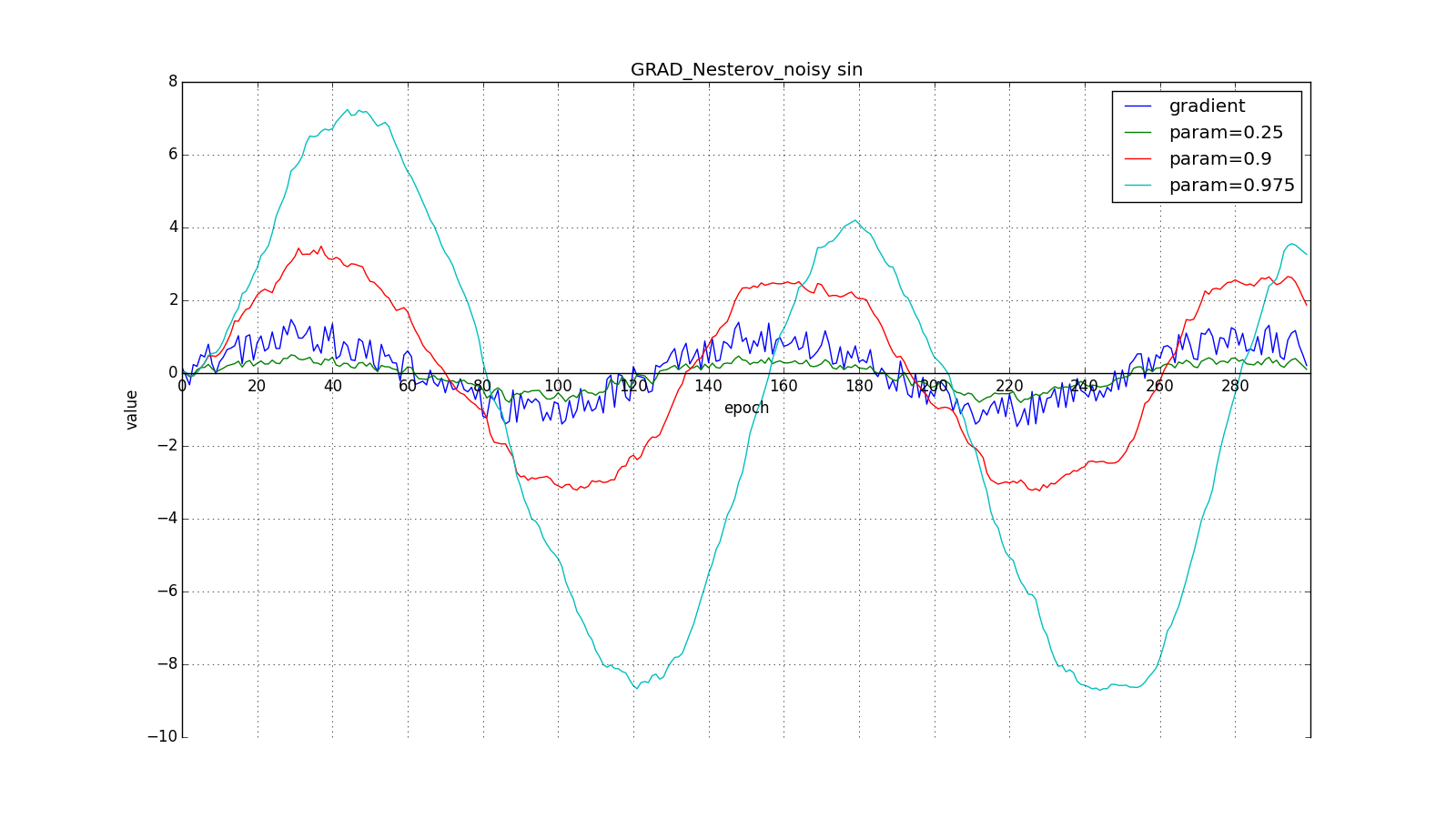
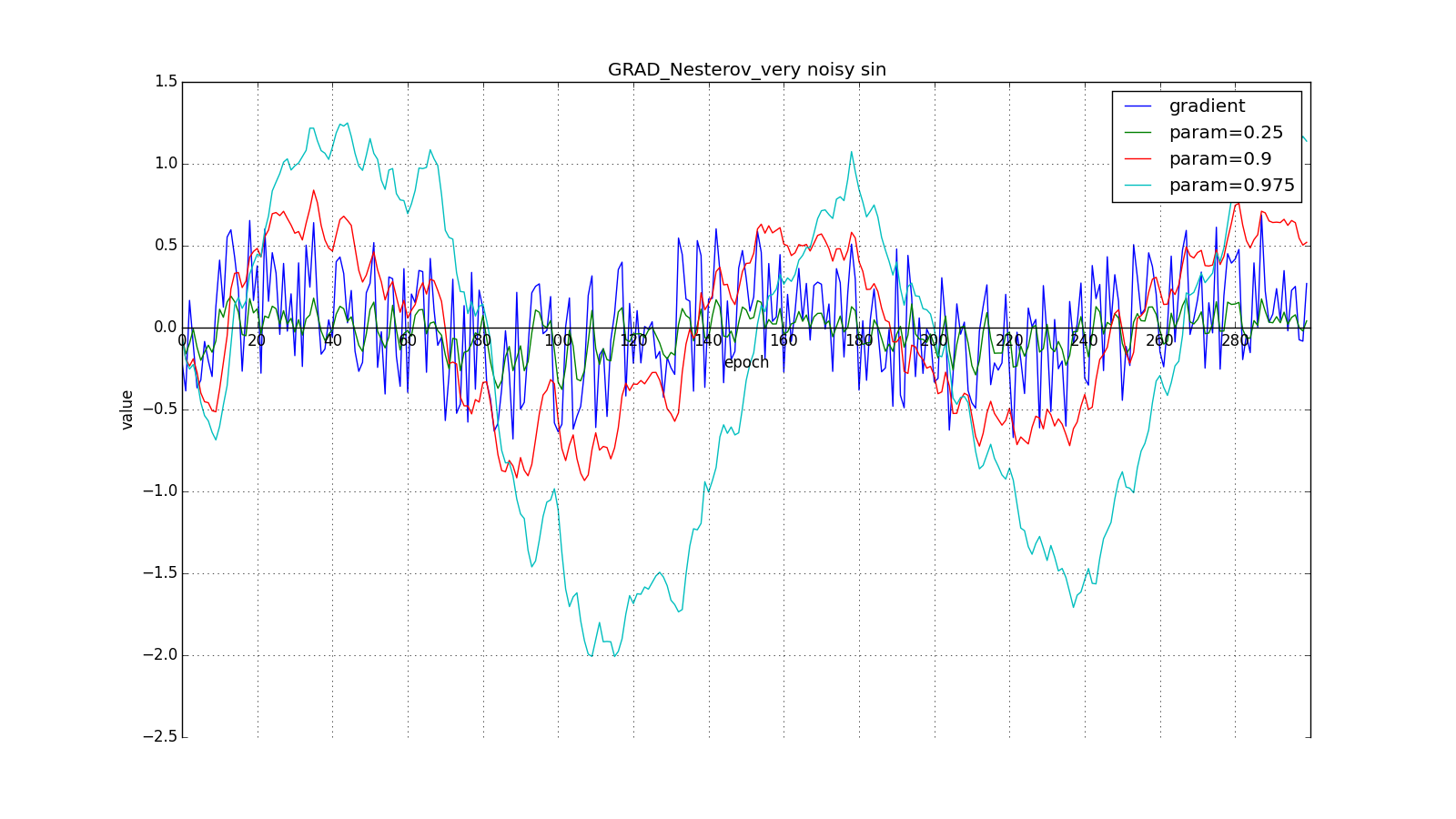
Заглядывание вперёд может сыграть с нами злую шутку, если установлены слишком большие $\inline \gamma$ и $\inline \eta$ : мы заглядываем настолько далеко, что промахиваемся мимо областей с противоположным знаком градиента:

Впрочем, иногда такое поведение может оказаться желательным. Ещё раз обращу ваше внимание на идею — заглядывание вперёд —, а не на исполнение. Метод Нестерова (6) — самый очевидный вариант, но не единственный. Например, можно воспользоваться ещё одним приёмом из вычислительной математики — стабилизацией градиента усреднением по нескольким точкам вдоль прямой, по которой мы двигаемся. Скажем, так:

$(8)$

$v_t = \gamma v_{t-1} + \frac{\eta}{3} \big( \nabla_\theta J( \theta - \frac{\gamma v_{t-1}}{3} ) + \nabla_\theta J( \theta - \frac{2\gamma v_{t-1}}{3} ) + \nabla_\theta J( \theta - \gamma v_{t-1} ) \big)$

Или так:

$(9)$

$v_t = \gamma v_{t-1} + \frac{\eta}{7} \big( \nabla_\theta J( \theta - \frac{\gamma v_{t-1}}{2} ) + 2\nabla_\theta J( \theta - \frac{3\gamma v_{t-1}}{4} ) + 4\nabla_\theta J( \theta - \gamma v_{t-1} ) \big)$

Такой приём может помочь в случае шумных целевых функций.

Мы не будем манипулировать аргументом целевой функции в последующих методах (хотя вам, разумеется, никто не мешает поэкспериментировать). Далее для краткости

$(10)$

$g_t \equiv \nabla_\theta J( \theta_t )$

Adagrad

Как работают методы с накоплением импульса представляют себе многие. Перейдём же к более интересным алгоритмам оптимизации. Начём со сравнительно простого Adagrad — adaptive gradient.

Некоторые признаки могут быть крайне информативными, но встречаться редко. Экзотическая высокооплачиваемая профессия, причудливое слово в спам-базе — они запросто потонут в шуме всех остальных обновлений. Речь идёт не только о редко встречающихся входных параметрах. Скажем, вам вполне могут встретиться редкие графические узоры, которые и в признак-то превращаются только после прохождения через несколько слоёв свёрточной сети. Хорошо бы уметь обновлять параметры с оглядкой на то, насколько типичный признак они фиксируют. Достичь этого несложно: давайте будем хранить для каждого параметра сети сумму квадратов его обновлений. Она будет выступать в качестве прокси для типичности: если параметр принадлежит цепочке часто активирующихся нейронов, его постоянно дёргают туда-сюда, а значит сумма быстро накапливается. Перепишем формулу обновления вот так:

$(11)$

$G_{t} = G_{t} + g_{t}^2$

$(12)$

$\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{G_{t} + \epsilon}} g_{t}$

Где $\inline G_{t}$ — сумма квадратов обновлений, а $\inline \epsilon$ — сглаживающий параметр, необходимый, чтобы избежать деления на 0. У часто обновлявшегося в прошлом параметра большая $\inline G_t$ , значит большой знаменатель в (12). Параметр изменившийся всего раз или два обновится в полную силу. $\inline \epsilon$ берут порядка $\inline 10^{-6}$ или $\inline 10^{-8}$ для совсем агрессивного обновления, но, как видно из графиков, это играет роль только в начале, ближе к середине обучение начинает перевешивать $\inline G_t$ :

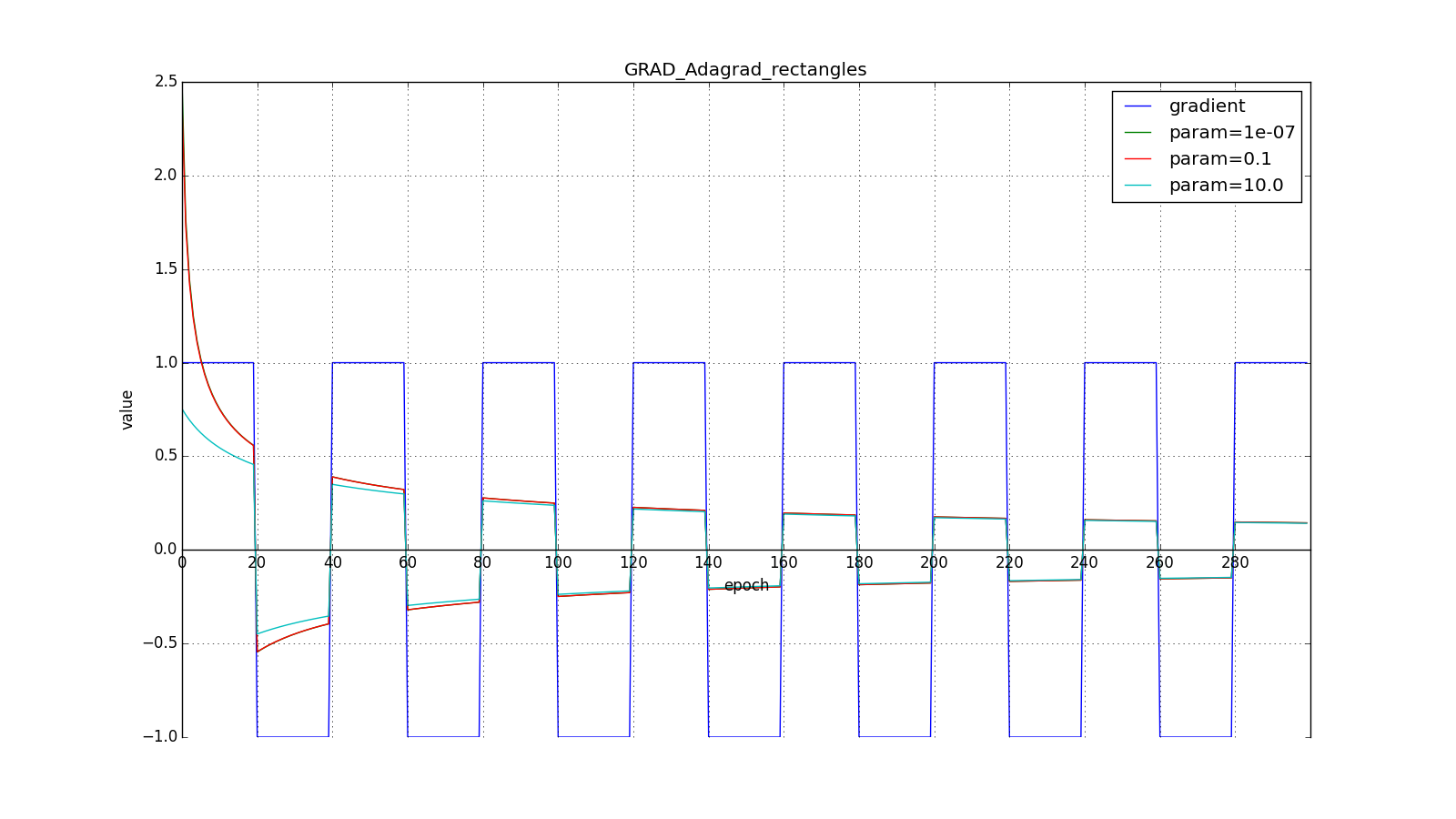
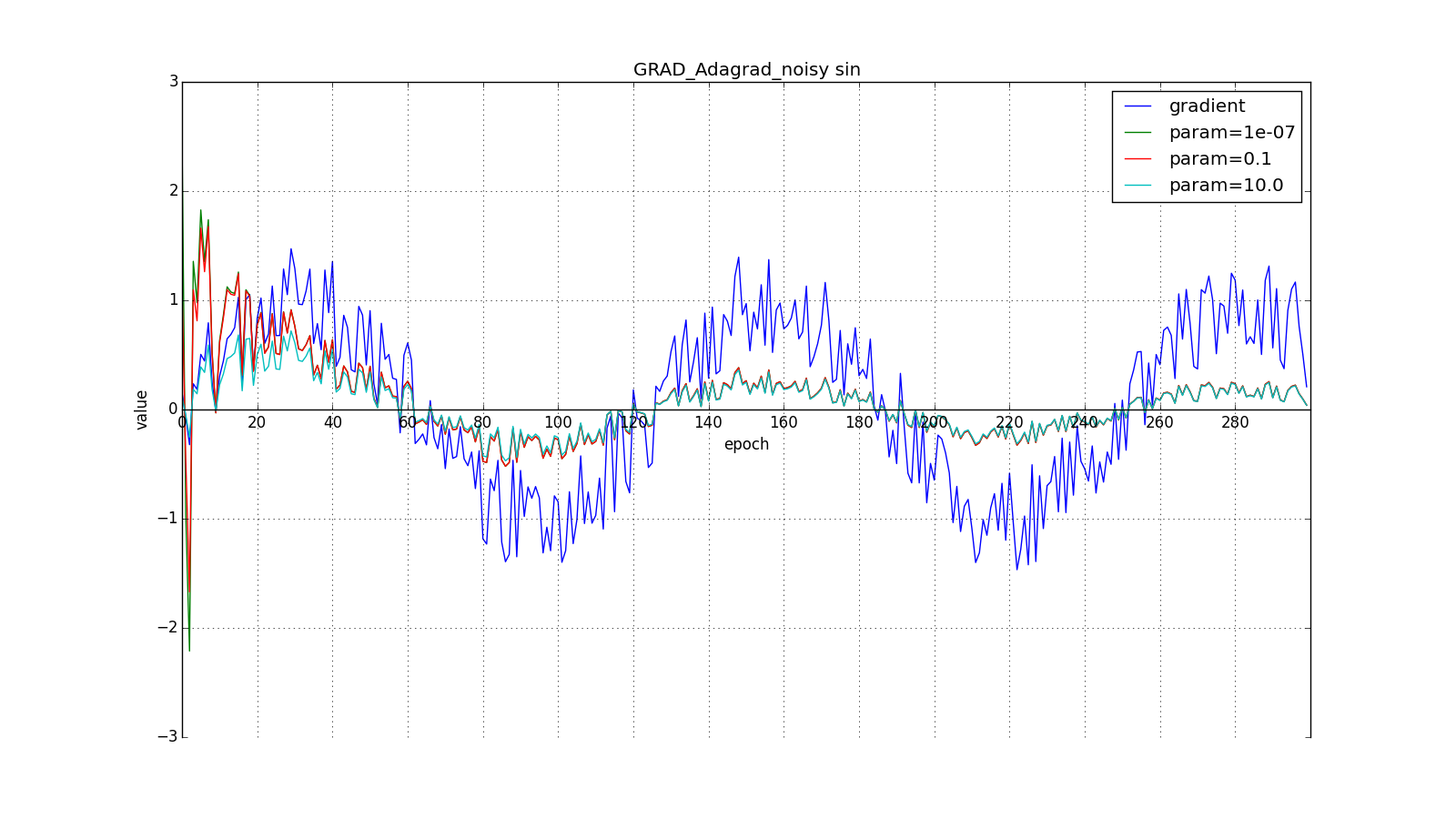
Итак, идея Adagrad в том, чтобы использовать что-нибудь, что бы уменьшало обновления для элементов, которые мы и так часто обновляем. Никто нас не заставляет использовать конкретно эту формулу, поэтому Adagrad иногда называют семейством алгоритмов. Скажем, мы можем убрать корень или накапливать не квадраты обновлений, а их модули, или вовсе заменить множитель на что-нибудь вроде $\inline e^{-G_{t}}$ .

(Другое дело, что это требует экспериментов. Если убрать корень, обновления начнут уменьшаться слишком быстро, и алгоритм ухудшится)

Ещё одно достоинство Adagrad — отсутствие необходимости точно подбирать скорость обучения. Достаточно выставить её в меру большой, чтобы обеспечить хороший запас, но не такой громадной, чтобы алгроритм расходился. По сути мы автоматически получаем затухание скорости обучения (learning rate decay).

RMSProp и Adadelta

Недостаток Adagrad в том, что $\inline G_{t}$ в (12) может увеличиваться сколько угодно, что через некоторое время приводит к слишком маленьким обновлениям и параличу алгоритма. RMSProp и Adadelta призваны исправить этот недостаток.

Модифицируем идею Adagrad: мы всё так же собираемся обновлять меньше веса, которые слишком часто обновляются, но вместо полной суммы обновлений, будем использовать усреднённый по истории квадрат градиента. Снова используем экспоненциально затухающее бегущее среднее
(4). Пусть $\inline E[g^2]_t$ — бегущее среднее в момент $\inline t$

$(13)$

$E[g^2]_t = \gamma E[g^2]_{t-1} + (1 - \gamma) g^2_t$

тогда вместо (12) получим

$(14)$

$\theta_{t+1} = \theta_{t} - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t}$

Знаменатель есть корень из среднего квадратов градиентов, отсюда RMSProp — root mean square propagation

$(15)$

$RMS[g]_t = \sqrt{E[g^2]_t + \epsilon}$

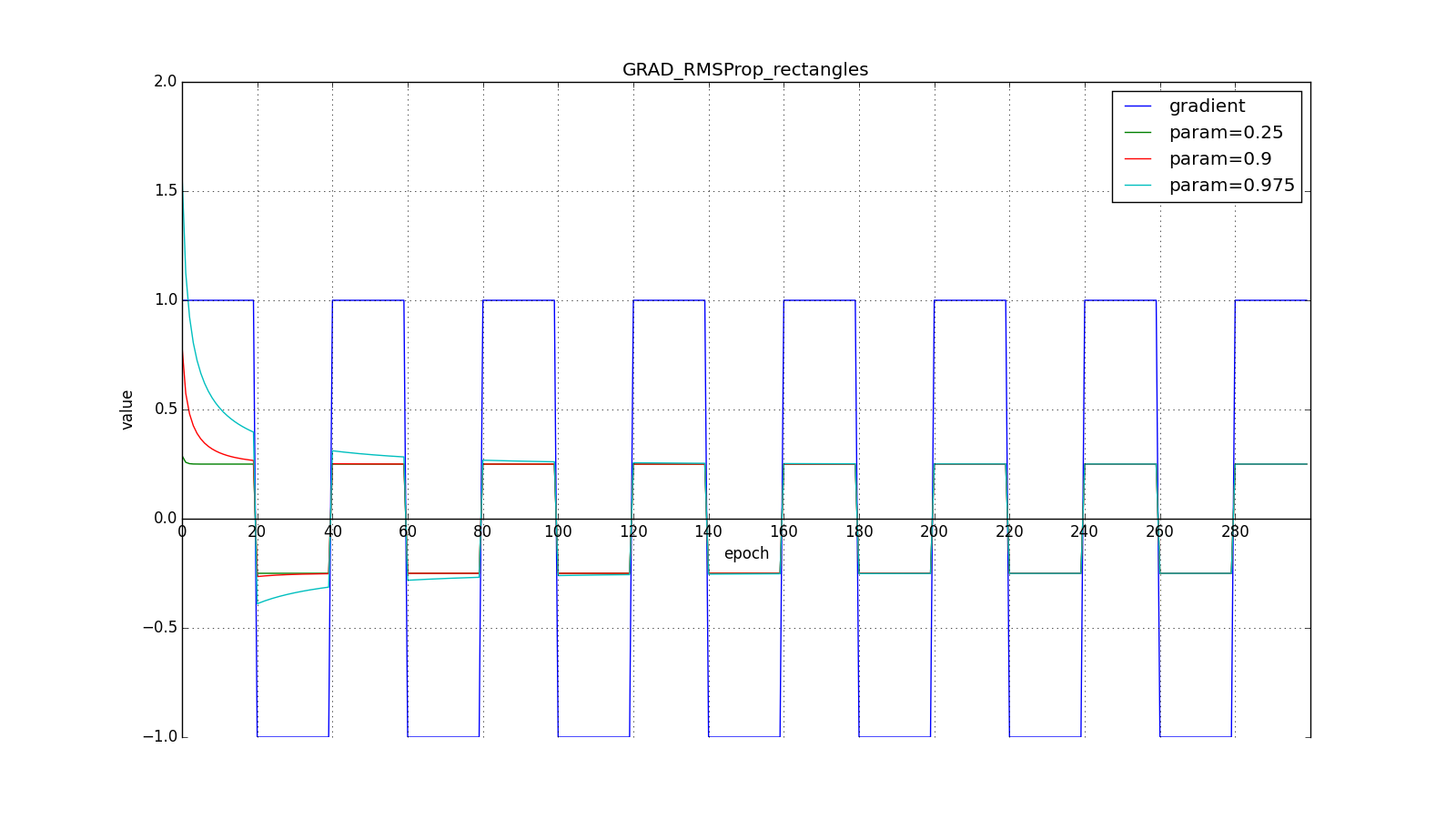
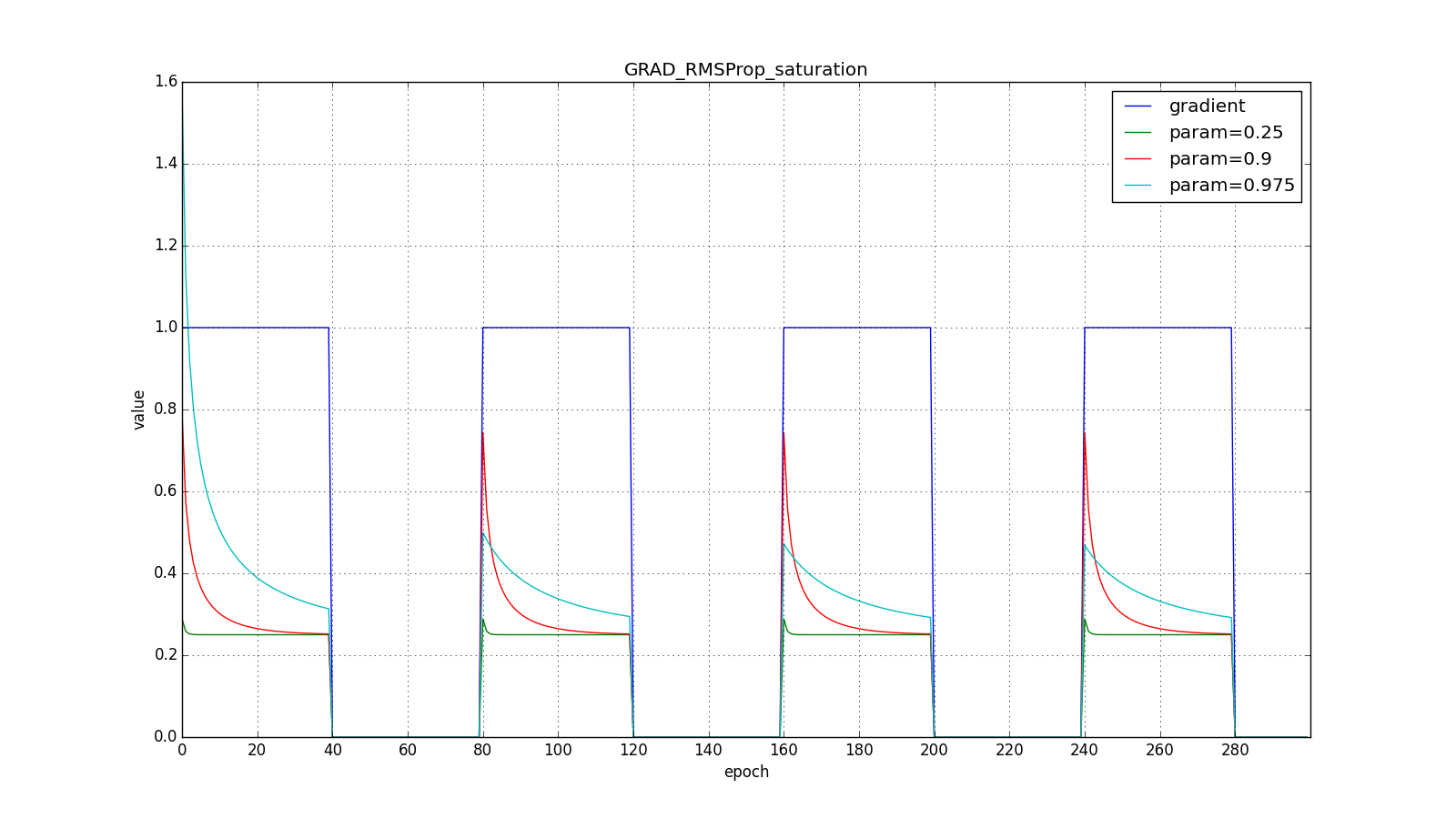
Обратите внимание, как восстанавливается скорость обновления на графике с длинными зубцами для разных $\inline \gamma$ . Также сравните графики с меандром для Adagrad и RMSProp: в первом случае обновления уменьшаются до нуля, а во втором — выходят на определённый уровень.

Вот и весь RMSProp. Adadelta от него отличается тем, что мы добавляем в числитель (14) стабилизирующий член пропорциональный $\inline RMS$ от $\inline \Delta\theta_t$ . На шаге $\inline t$ мы ещё не знаем значение $\inline RMS[\Delta \theta]_{t}$ , поэтому обновление параметров происходит в три этапа, а не в два: сначала накапливаем квадрат градиента, затем обновляем $\inline \theta$ , после чего обновляем $\inline RMS[\Delta \theta]$ .

$(16)$

$\Delta \theta = -\frac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}}g_{t}$

$(17)$

$\theta_{t+1} = \theta_{t} - \frac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}}g_{t}$

$(18)$

$E[\Delta \theta^2]_t = \gamma E[\Delta \theta^2]_{t-1} + (1 - \gamma) \Delta \theta^2_t$

$(19)$

$RMS[\Delta \theta]_{t} = \sqrt{E[\Delta \theta^2]_t + \epsilon}$

Такое изменение сделано из соображений, что размерности $\inline \theta$ и $\inline \Delta \theta$ должны совпадать. Заметьте, что learning rate не имеет размерности, а значит во всех алгоритмах до этого мы складывали размерную величину с безразмерной. Физики в этом месте ужаснутся, а мы пожмём плечами: работает же.

Заметим, что нам нужен ненулевой $\inline RMS[\Delta \theta]_{-1}$ для первого шага, иначе все последующие $\inline \Delta \theta$ , а значит и $\inline RMS[\Delta \theta]_{t}$ будут равны нулю. Но эту проблему мы решили ещё раньше, добавив в $\inline RMS$ $\inline \epsilon$ . Другое дело, что без явного большого $\inline RMS[\Delta \theta]_{-1}$ мы получим поведение, противоположное Adagrad и RMSProp: мы будем сильнее (до некоторого предела) обновлять веса, которые используются чаще. Ведь теперь чтобы $\inline \Delta \theta$ стал значимым, параметр должен накопить большую сумму в числителе дроби.

Вот графики для нулевого начального $\inline RMS[\Delta \theta]$ :

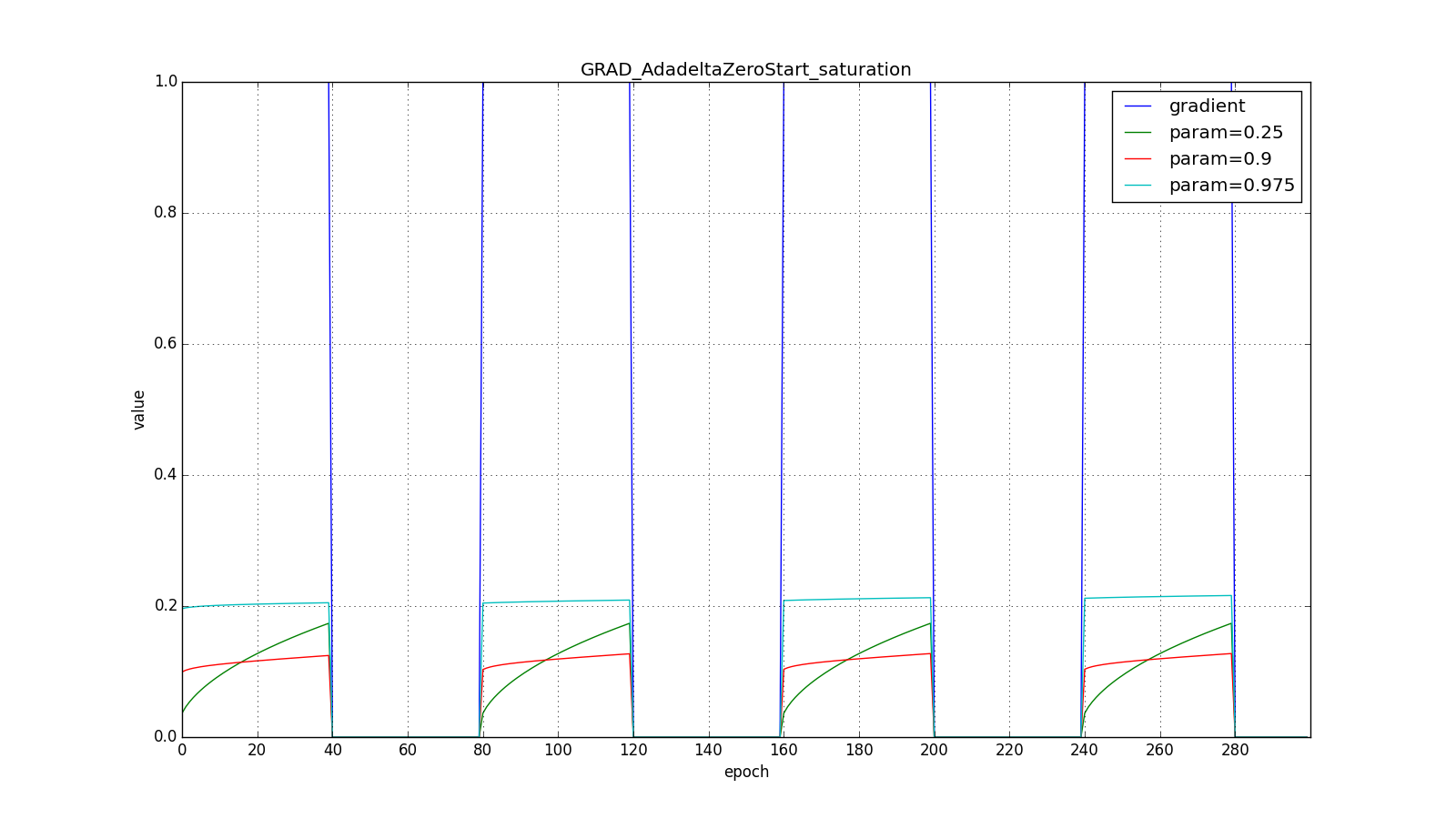
А вот для большого:

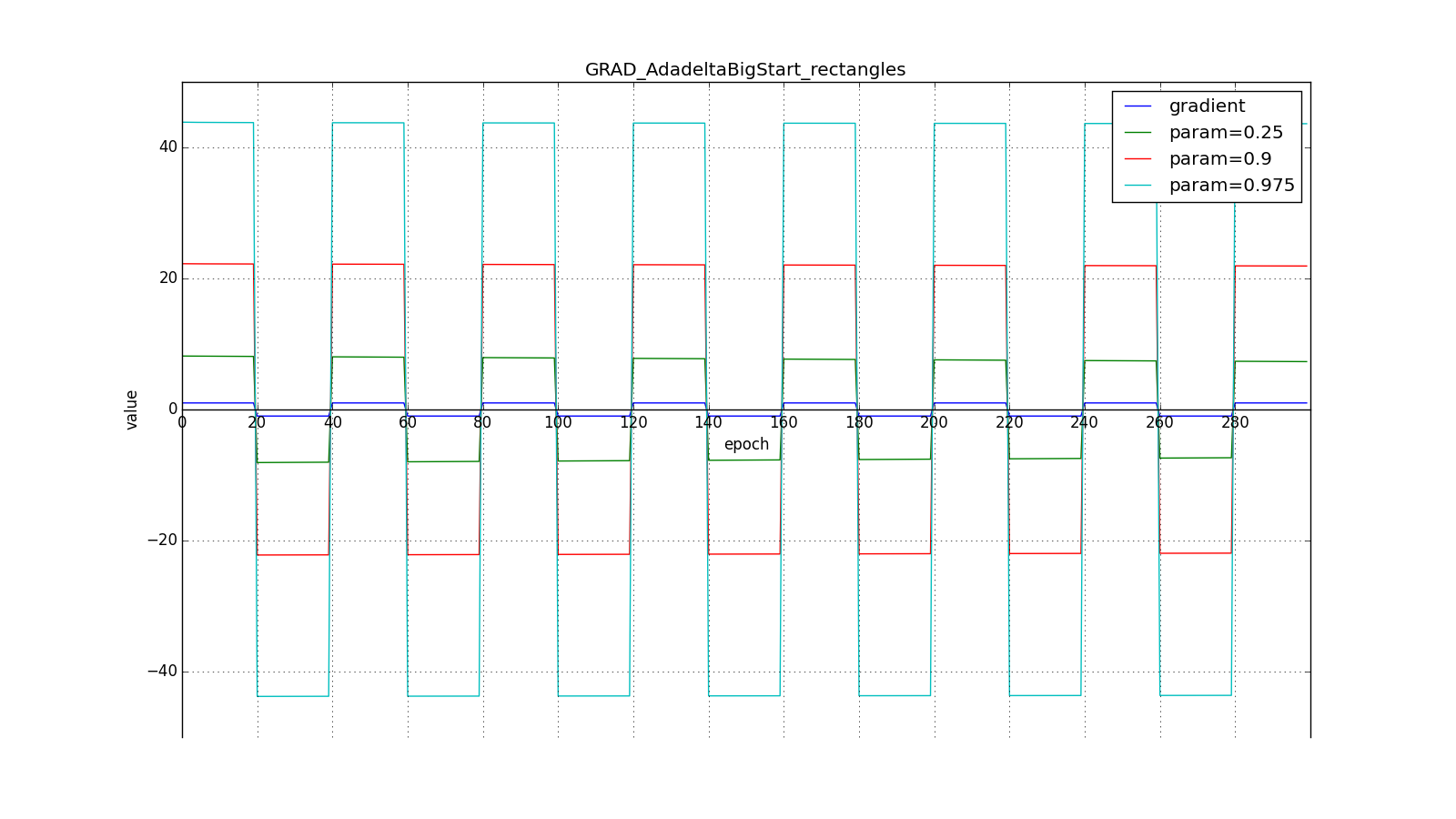
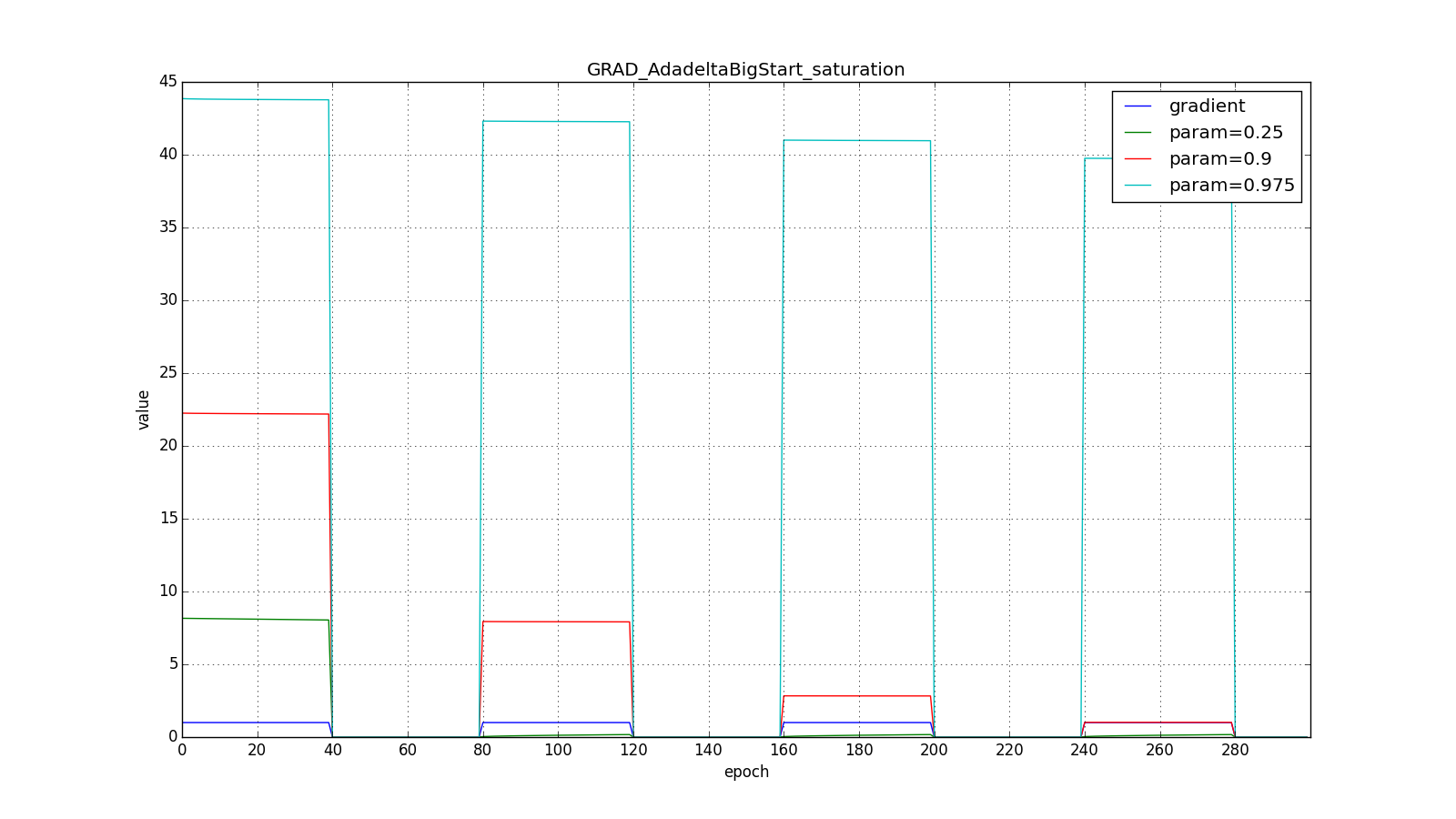
Впрочем, похоже, авторы алгоритма и добивались такого эффекта. Для RMSProp и Adadelta, как и для Adagrad не нужно очень точно подбирать скорость обучения — достаточно прикидочного значения. Обычно советуют начать подгон $\inline \eta$ c $\inline 0.1 - 1$ , a $\inline \gamma$ так и оставить $\inline 0.9$ . Чем ближе $\inline \gamma$ к $\inline 1$ , тем дольше RMSProp и Adadelta с большим $\inline RMS[\Delta \theta]_{-1}$ будут сильно обновлять мало используемые веса. Если же $\inline \gamma \approx 1$ и $\inline RMS[\Delta \theta]_{-1} = 0$ , то Adadelta будет долго «с недоверием» относиться к редко используемым весам. Последнее может привести к параличу алгоритма, а может вызвать намеренно «жадное» поведение, когда алгоритм сначала обновляет нейроны, кодирующие самые лучшие признаки.

Adam

Adam — adaptive moment estimation, ещё один оптимизационный алгоритм. Он сочетает в себе и идею накопления движения и идею более слабого обновления весов для типичных признаков. Снова вспомним (4):

$(20)$

$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$

От Нестерова Adam отличается тем, что мы накапливаем не $\inline \Delta \theta$ , а значения градиента, хотя это чисто косметическое изменение, см. (23). Кроме того, мы хотим знать, как часто градиент изменяется. Авторы алгоритма предложили для этого оценивать ещё и среднюю нецентрированную дисперсию:

$(21)$

$v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$

Легко заметить, что это уже знакомый нам $\inline E[g^2]_t$ , так что по сути тут нет отличий от RMSProp.

Важное отличие состоит в начальной калибровке $\inline m_t$ и $\inline v_t$ : они страдают от той же проблемы, что и $\inline E[g^2]_t$ в RMSProp: если задать нулевое начальное значение, то они будут долго накапливаться, особенно при большом окне накопления ( $\inline 0 \ll \beta_1 < 1$ , $\inline 0 \ll \beta_2 < 1$ ), а какие-то изначальные значения — это ещё два гиперпараметра. Никто не хочет ещё два гиперпараметра, так что мы искусственно увеличиваем $\inline m_t$ и $\inline v_t$ на первых шагах (примерно $\inline 0 < t < 10$ для $\inline m_t$ и $\inline 0 < t < 1000$ для $\inline v_t$ )

$(22)$

$\hat{m}_t = \frac{m_t}{1 - \beta^t_1}, \; \hat{v}_t = \frac{v_t}{1 - \beta^t_2}$

В итоге, правило обновления:

$(23)$

$\theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t + \epsilon}} \hat{m}_t$

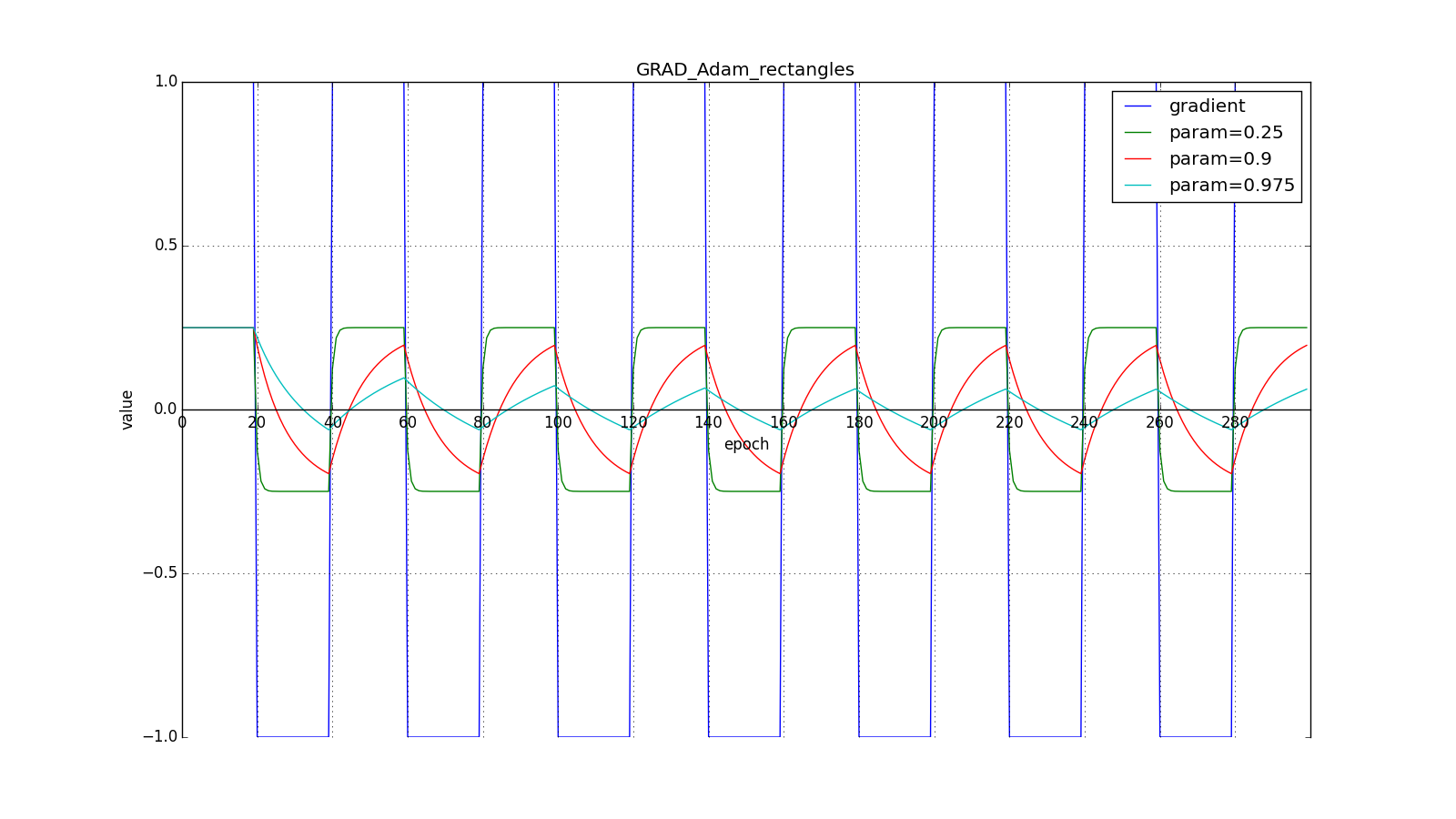
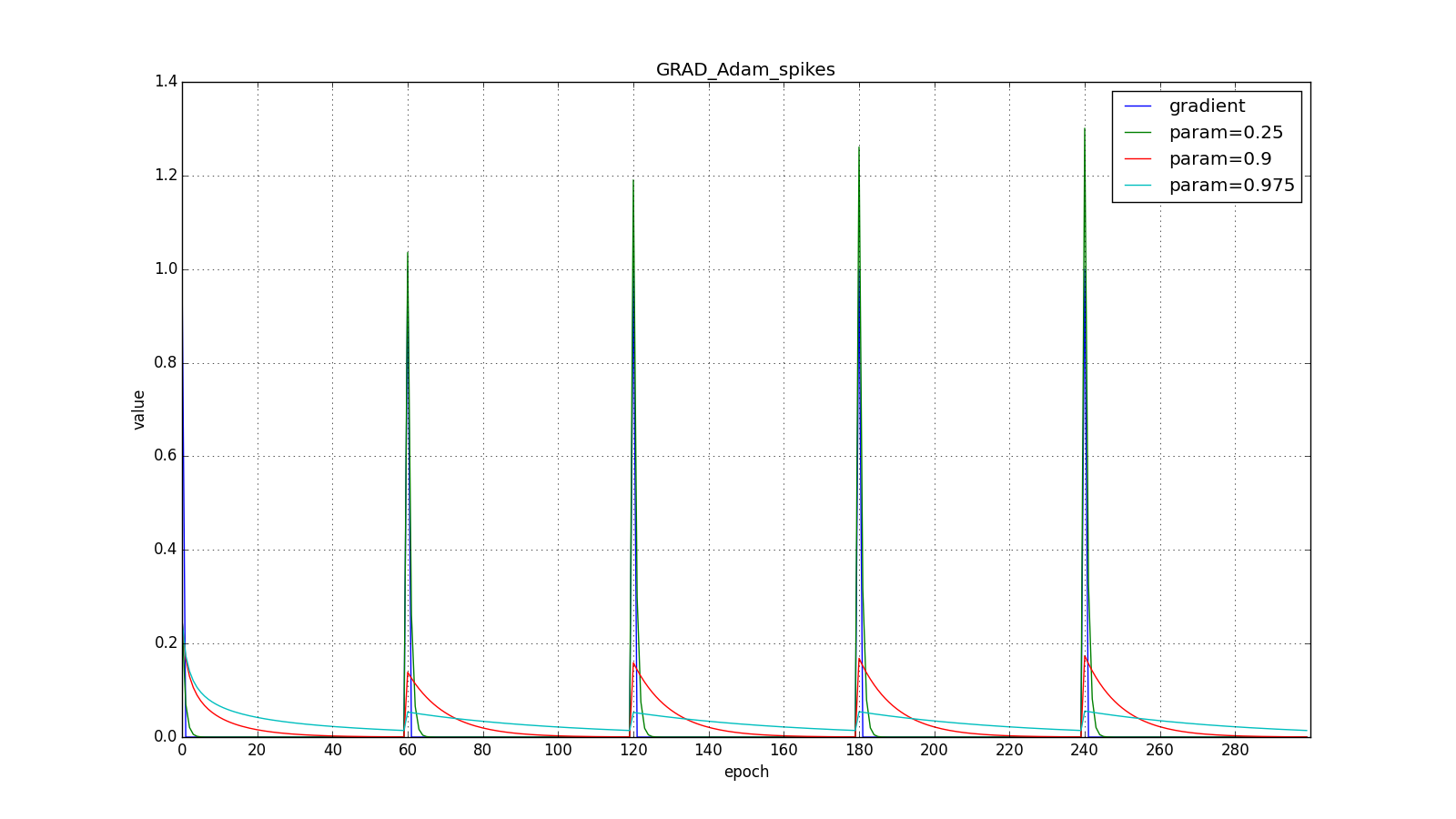
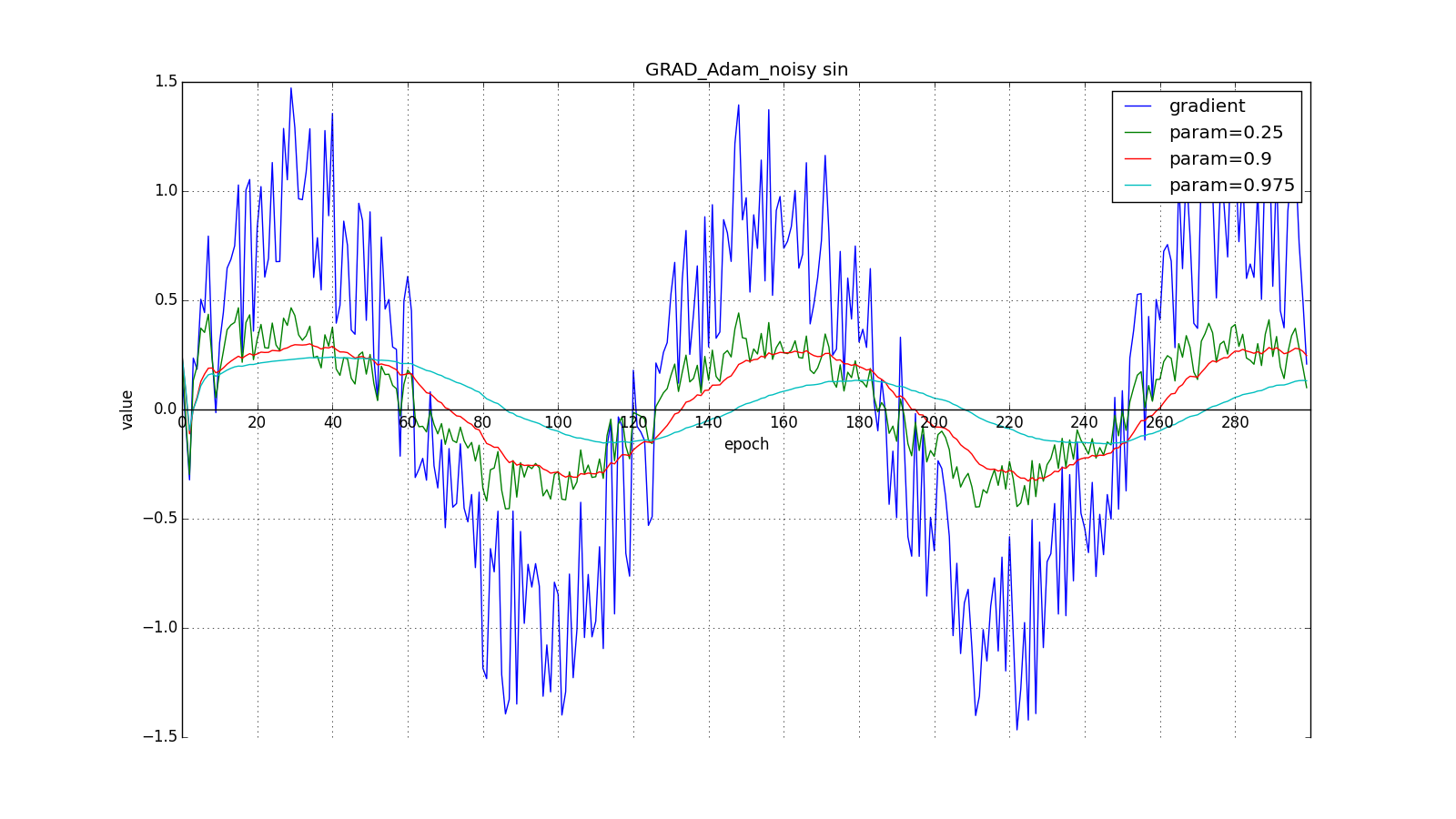
Здесь следует внимательно посмотреть на то, как быстро синхронизировались значения обновлений на первых зубцах графиков с прямоугольниками и на гладкость кривой обновлений на графике с синусом — её мы получили «бесплатно». При рекомендуемом параметре $\inline \beta_1$ на графике с шипами видно, что резкие всплески градиента не вызывает мгновенного отклика в накопленном значении, поэтому хорошо настроенному Adam не нужен gradient clipping.

Авторы алгоритма выводят (22), разворачивая рекурсивные формулы (20) и (21). Например, для $\inline v_t$ :

$E[v_t] &= E\Bigg[ (1 - \beta_2) \sum_{i=1}^{t}{\beta_2^{t-i}g_i^2} \Bigg]$

$= E[g_t^2] (1 - \beta_2) \sum_{i=1}^{t}\beta_2^{t-i} + \zeta$

$= E[g_t^2] (1 - \beta_2) \frac{1 - \beta_2^t}{1 - \beta_2} + \zeta$

$(24)$

$= E[g_t^2](1 - \beta_2^t) + \zeta$

Слагаемое $\inline \zeta$ близко к $\inline 0$ при стационарном распределении $\inline p(g)$ , что неправда в практически интересующих нас случаях., но мы всё равно переносим скобку с $\inline \beta_2^t$ влево. Неформально, можно представить что при $\inline t=0$ у нас бесконечная история одинаковых обновлений:

$(25)$

$\hat{v}_1 = v_{1} + \beta_2 v_{1} + \beta_2^2 v_{1} + \ldots = \frac{v_{1}}{1 - \beta_2}$

Когда же мы получаем более близкое к правильному значение $\inline v$ , мы заставляем «виртуальную» часть ряда затухать быстрее:

$(26)$

$\hat{v}_2 = v_{2} + \beta_2^2 v_{2} + \beta_2^4 v_{2} + \ldots = \frac{v_{2}}{1 - \beta_2^2}$

Авторы Adam предлагают в качестве значений по умолчанию $\inline \beta_1 = 0.9, \beta_2 = 0.999, \epsilon = 10^{-8}$ и утверждают, что алгоритм выступает лучше или примерно так же, как и все предыдущие алгоритмы на широком наборе датасетов за счёт начальной калибровки. Заметьте, что опять-таки, уравнения (22) не высечены в камне. У нас есть некоторое теоретическое обоснование, почему затухание должно выглядеть именно так, но никто не запрещает поэкспериментировать с формулами калибровки. На мой взгляд, здесь просто напрашивается применить заглядывание вперёд, как в методе Нестерова.

Adamax

Adamax как раз и есть такой эксперимент, предложенный в той же статье. Вместо дисперсии в (21) можно считать инерционный момент распределения градиентов произвольной степени $\inline p$ . Это может привести к нестабильности к вычислениям. Однако случай $\inline p$ , стремящейся к бесконечности, работает на удивление хорошо.

$(27)$

$v_t = \beta_2^p v_{t-1} + (1 - \beta_2^p) |g_t|^p$

Заметьте, что вместо $\inline \beta_2$ используется подходящий по размерности $\inline \beta_2^p$ . Кроме того, обратите внимание, чтобы использовать в формулах Adam значение, полученное в (27), требуется извлечь из него корень: $\inline u_t = v_t^{\frac{1}{p}}$ . Выведем решающее правило взамен (21), взяв $\inline p \rightarrow \infty$ , развернув под корнем $\inline v_t$ при помощи (27):

$u_t = \lim_{p \rightarrow \infty}{ v_t^{\frac{1}{p}} }$

$= \lim_{p \rightarrow \infty}{ \Big[ \beta_2^p v_{t-1} + (1 - \beta_2^p) |g_t|^p \Big]^{\frac{1}{p}} }$

$= \lim_{p \rightarrow \infty}{ \Big[ (1 - \beta_2^p) \sum_{i=1}^{t}\beta_2^{p(t-i)} |g_i|^{p} \Big]^{\frac{1}{p}} }$

$= \lim_{p \rightarrow \infty}{ (1 - \beta_2^p)^{\frac{1}{p}} \Big( \sum_{i=1}^{t}\beta_2^{p(t-i)}|g_i|^{p} \Big)^{\frac{1}{p}} }$

$= \lim_{p \rightarrow \infty}{ \Big( \sum_{i=1}^{t}\beta_2^{p(t-i)}|g_i|^{p} \Big)^{\frac{1}{p}} }$

$(28)$

$= max(\beta_2^{t-1} |g_1|, \beta_2^{t-2} |g_2|, \ldots , \beta_2|g_{t-1}|, |g_t| )$

Так получилось потому что при $\inline p \rightarrow \infty$ в сумме в (28) будет доминировать наибольший член. Неформально, можно интуитивно понять, почему так происходит, взяв простую сумму и большую $\inline p$ : $\inline \sqrt[100]{10^{100} + 9^{100}} = 10\sqrt[100]{1 + \frac{9}{10}^{100}} = 10\sqrt[10]{1.00002} \approx 10$ . Совсем не страшно.

Остальные шаги алгоритма такие же как и в Adam.

Эксперименты

Теперь давайте посмотрим на разные алгоритмы в деле. Чтобы было нагляднее, посмотрим на траекторию алгоритмов в задаче нахождения минимума функции двух переменных. Напомню, что обучение нейронной сети — это по сути то же самое, но переменных там значительно больше двух и вместо явно заданной функции у нас есть только набор точек, по котором мы хотим эту функцию построить. В нашем же случае функция потерь и есть целевая функция, по которой двигаются оптимизаторы. Конечно, на такой простой задаче невозможно почувствовать всю силу продвинутых алгоритмов, зато интуитивно понятно.

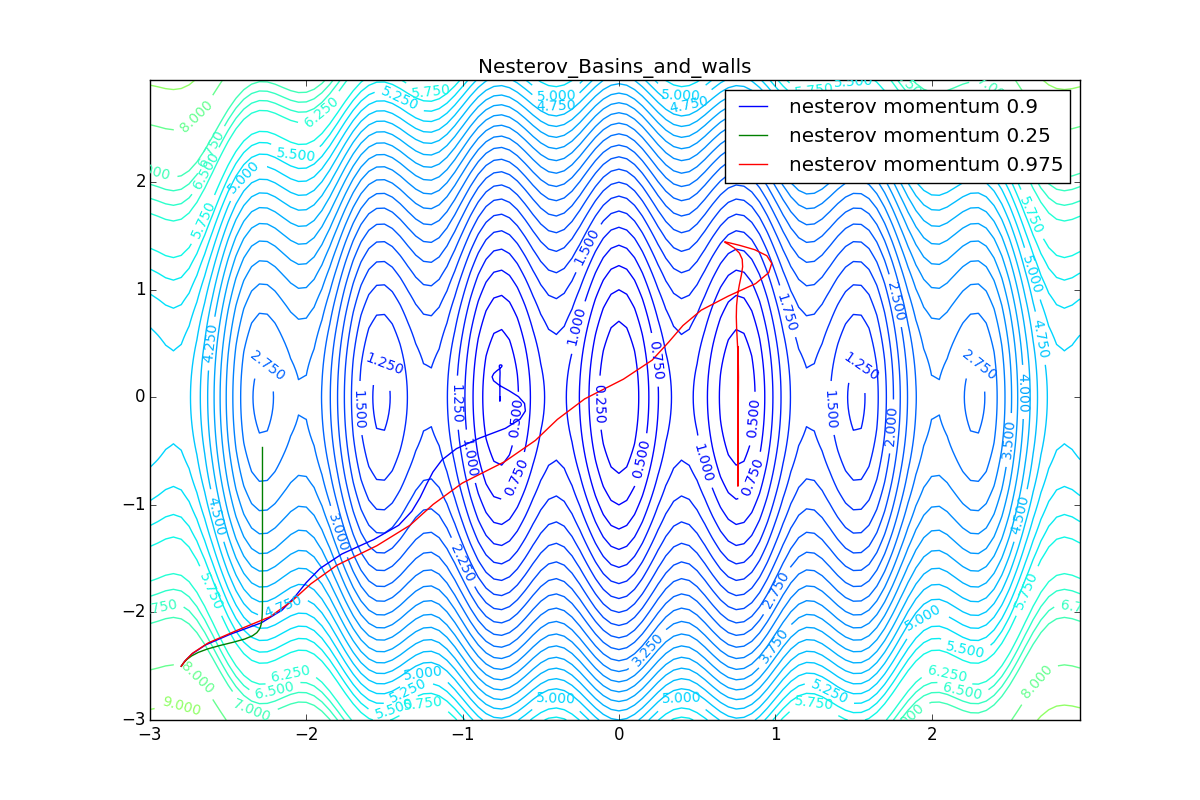
Для начала посмотрим на ускоренный градиент Нестерова с разными значениями $\inline \gamma$ . Поняв, почему выглядят именно так, проще понять и поведение всех остальных алгоритмов с накоплением импульса, включая Adam и Adamax.

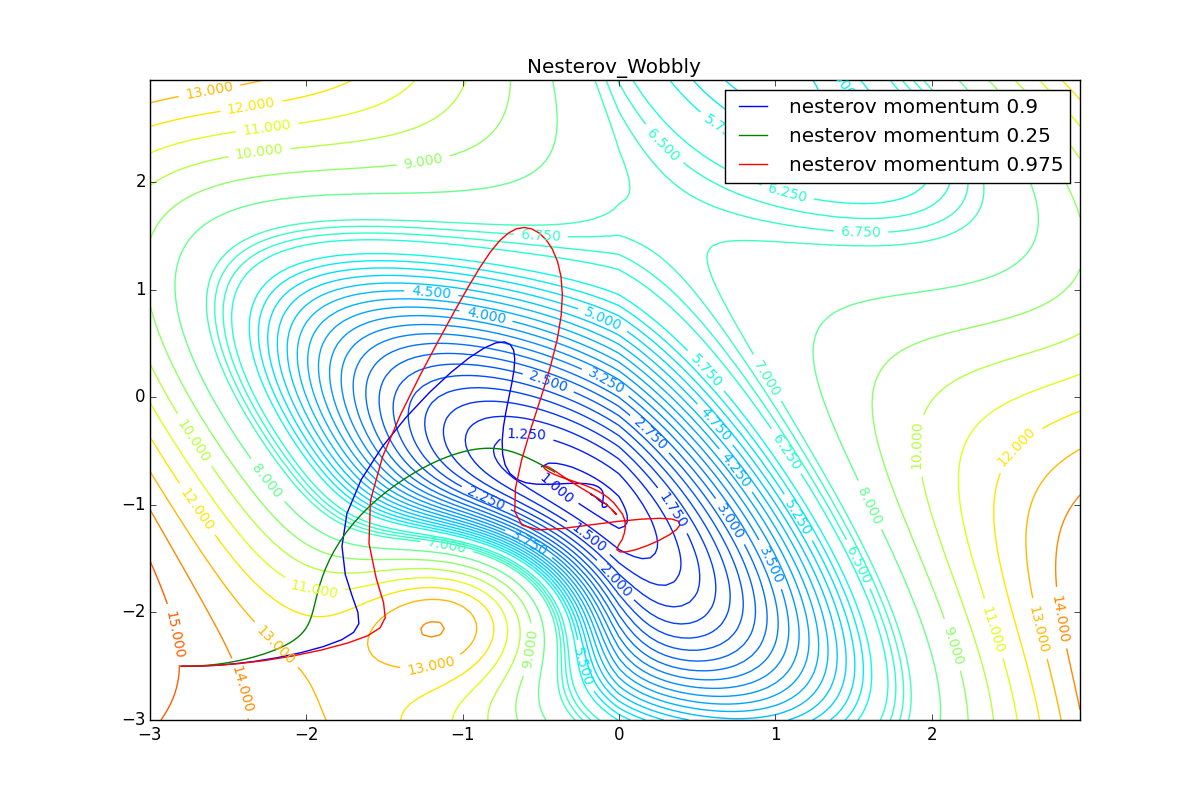
Все траектории оканчиваются в одном и том же бассейне, но делают они это по-разному. С маленьким $\inline \gamma$ алгоритм становится похож на обычный SGD, на каждом шаге спуск идёт в сторону убывающего градиента. Со слишком большим $\inline \gamma$ , начинает сильно влиять предыстория изменений, и траектория может сильно «гулять». Иногда это хорошо: чем больше накопленный импульс, тем проще вырваться из впадин локальных минимумов на пути.

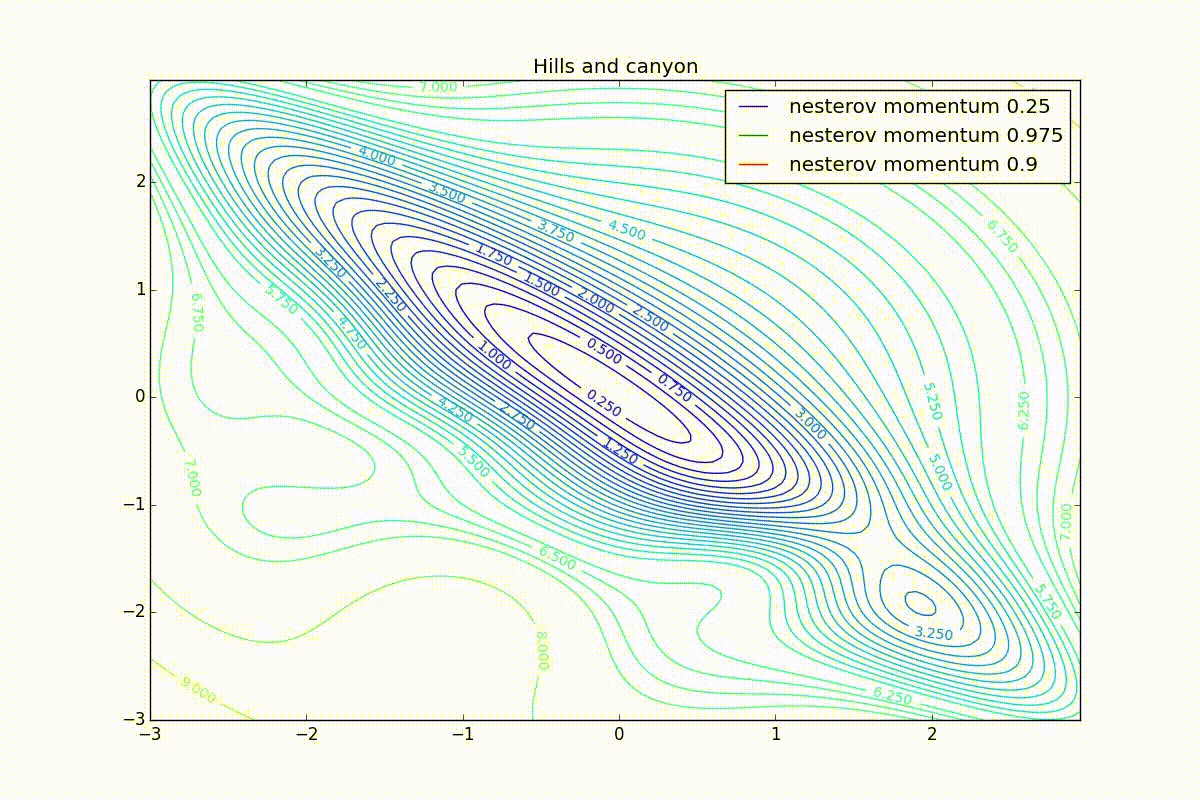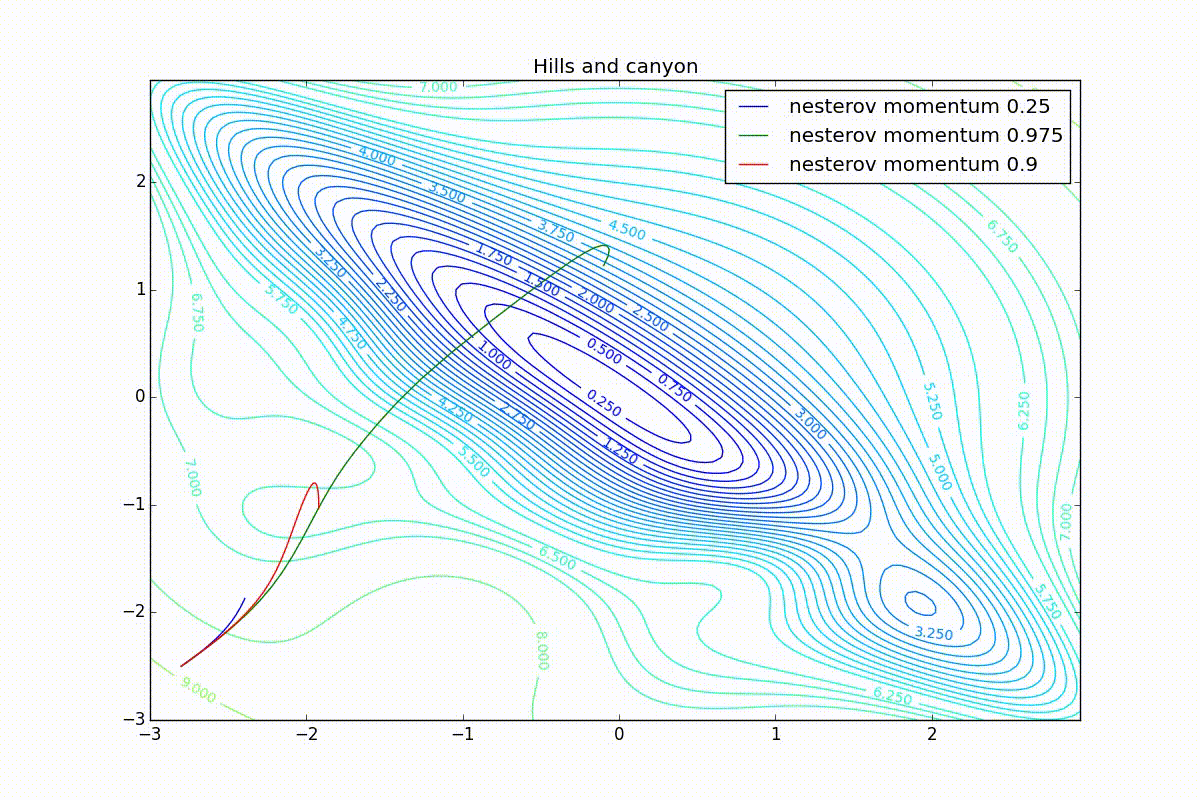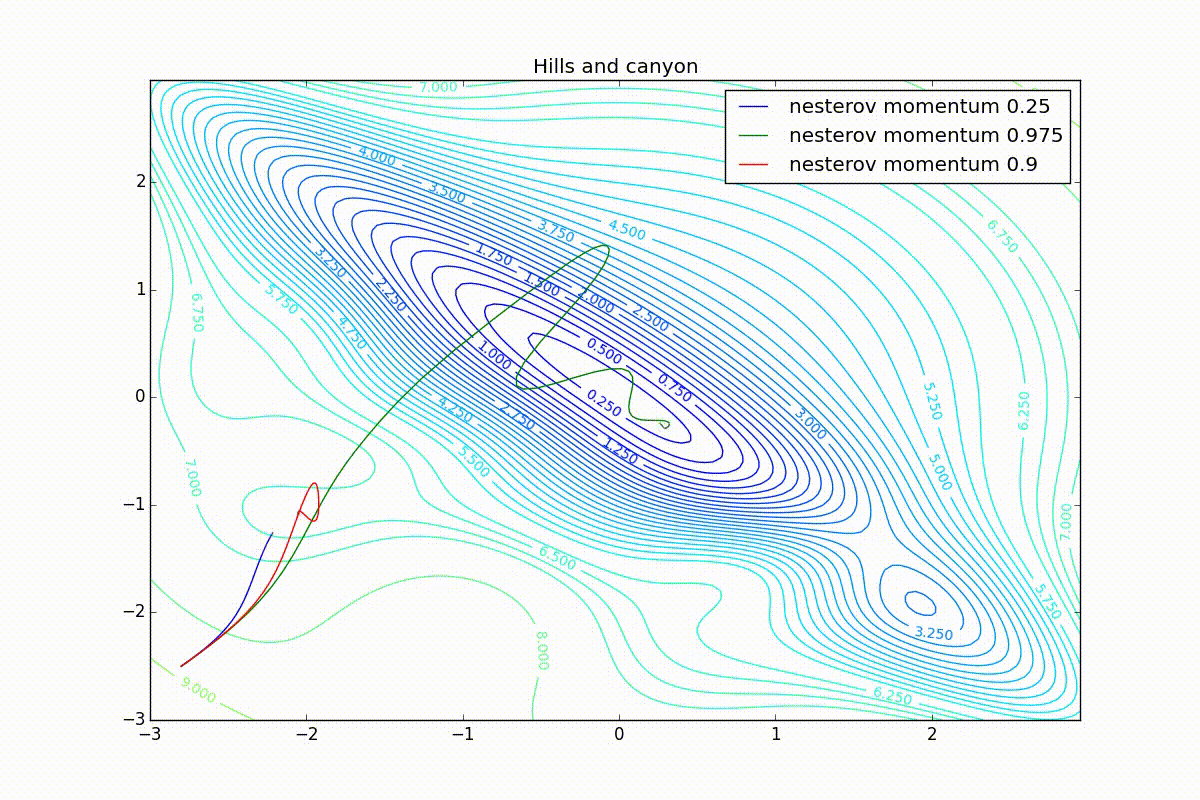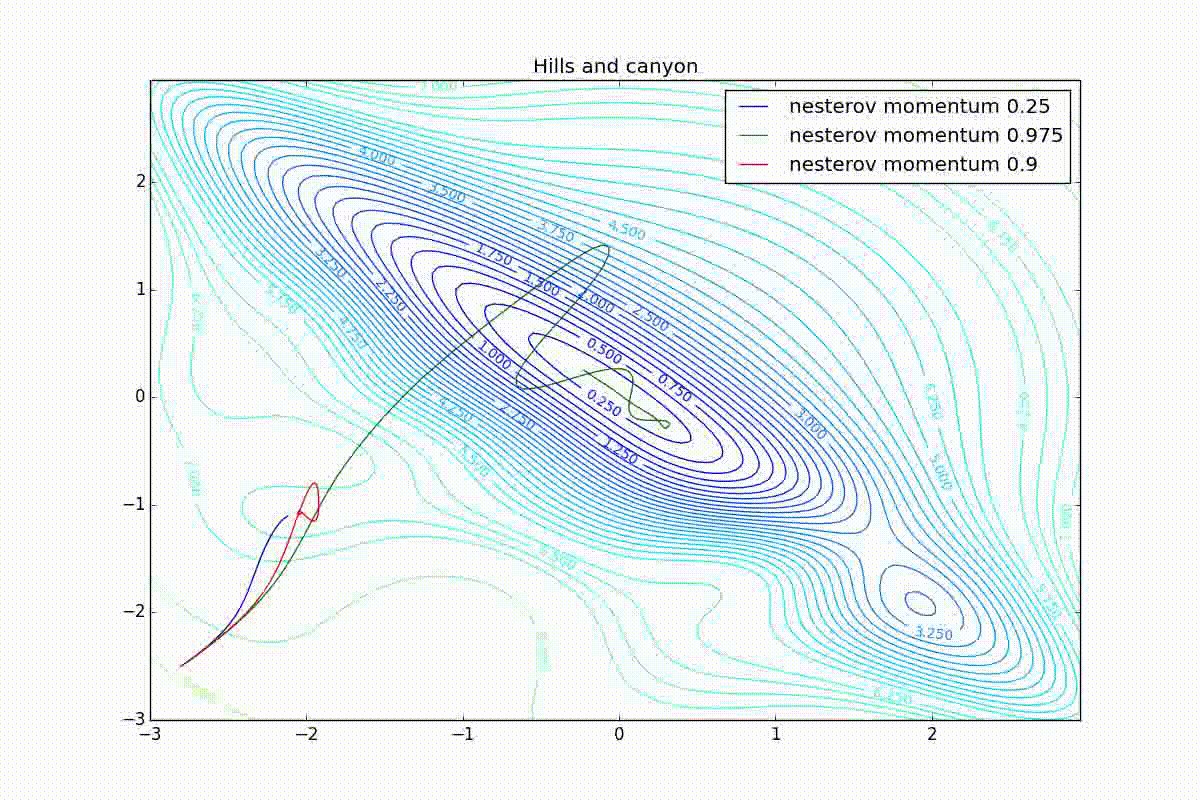
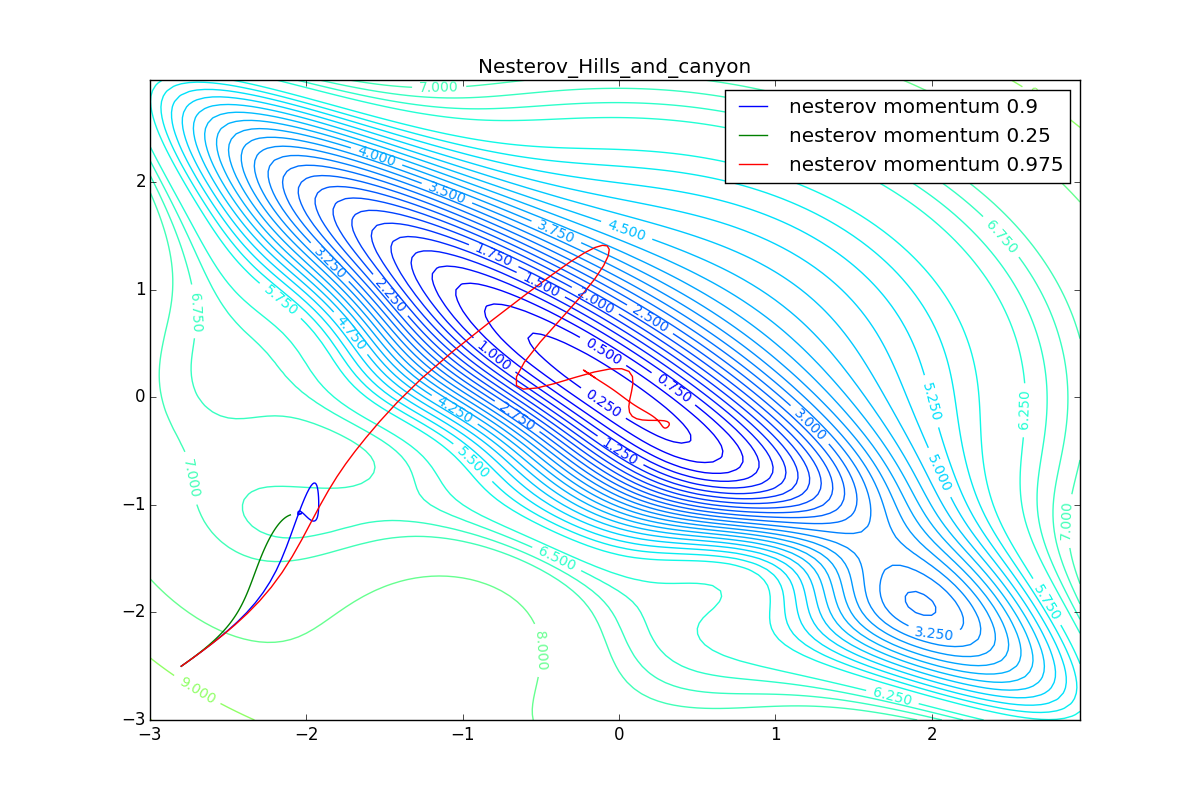
Иногда плохо: можно запросто растерять импульс, проскочив впадину глобального минимума и осесть в локальном. Поэтому при больших $\inline \gamma$ можно иногда увидеть, как потери на тренировочной выборке сначала достигают глобальный минимум, затем сильно возрастают, потом снова начинают опускаться, но так и не возвращаются в прошедший минимум.

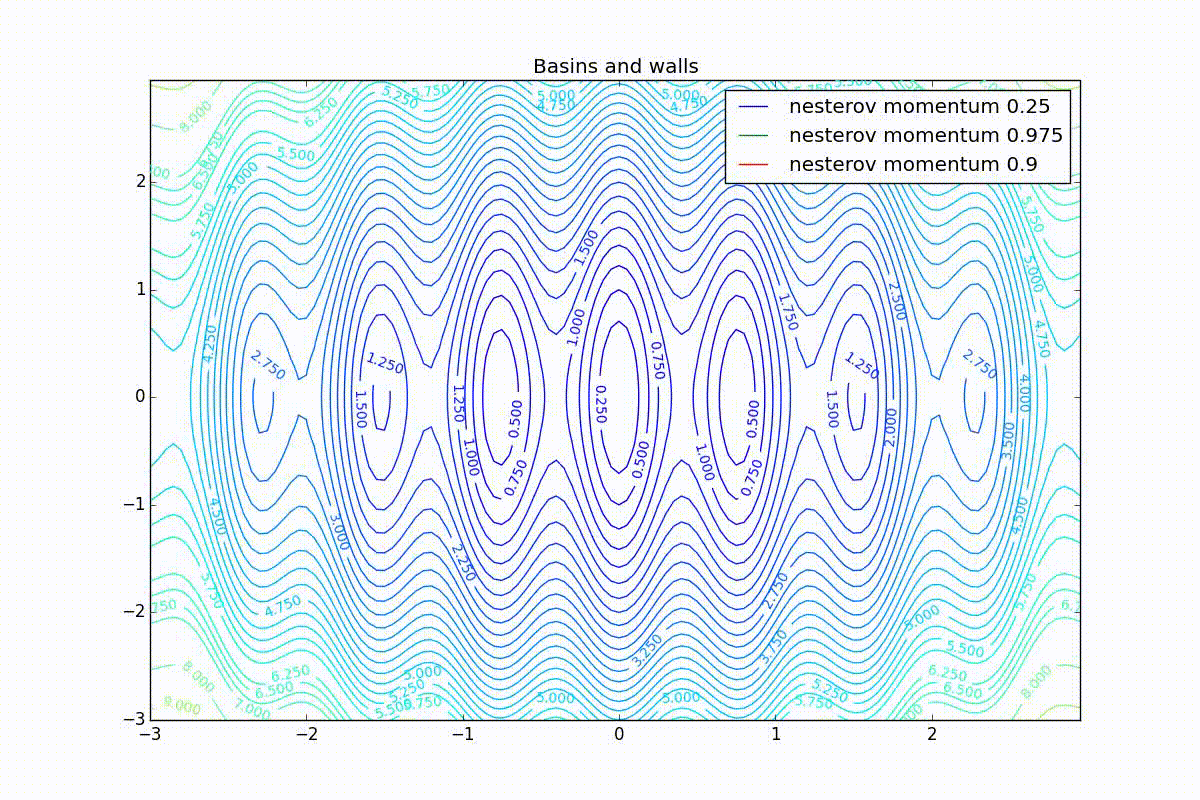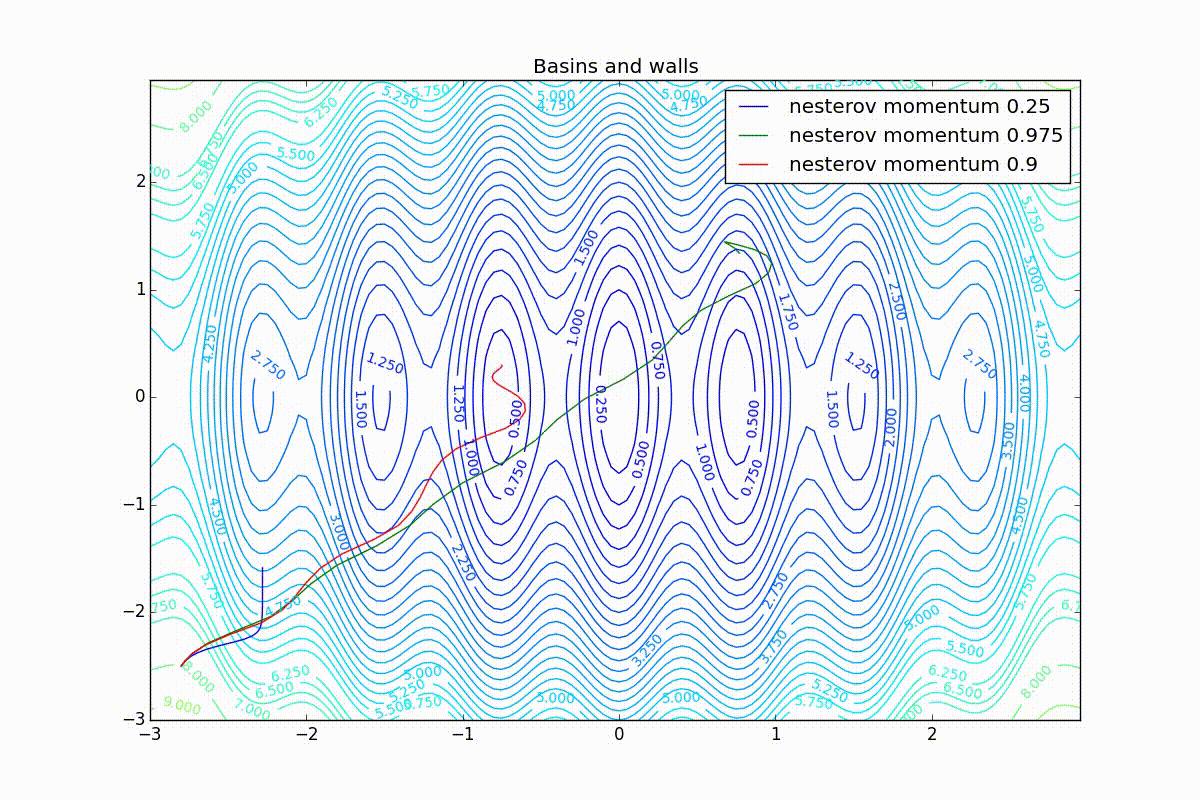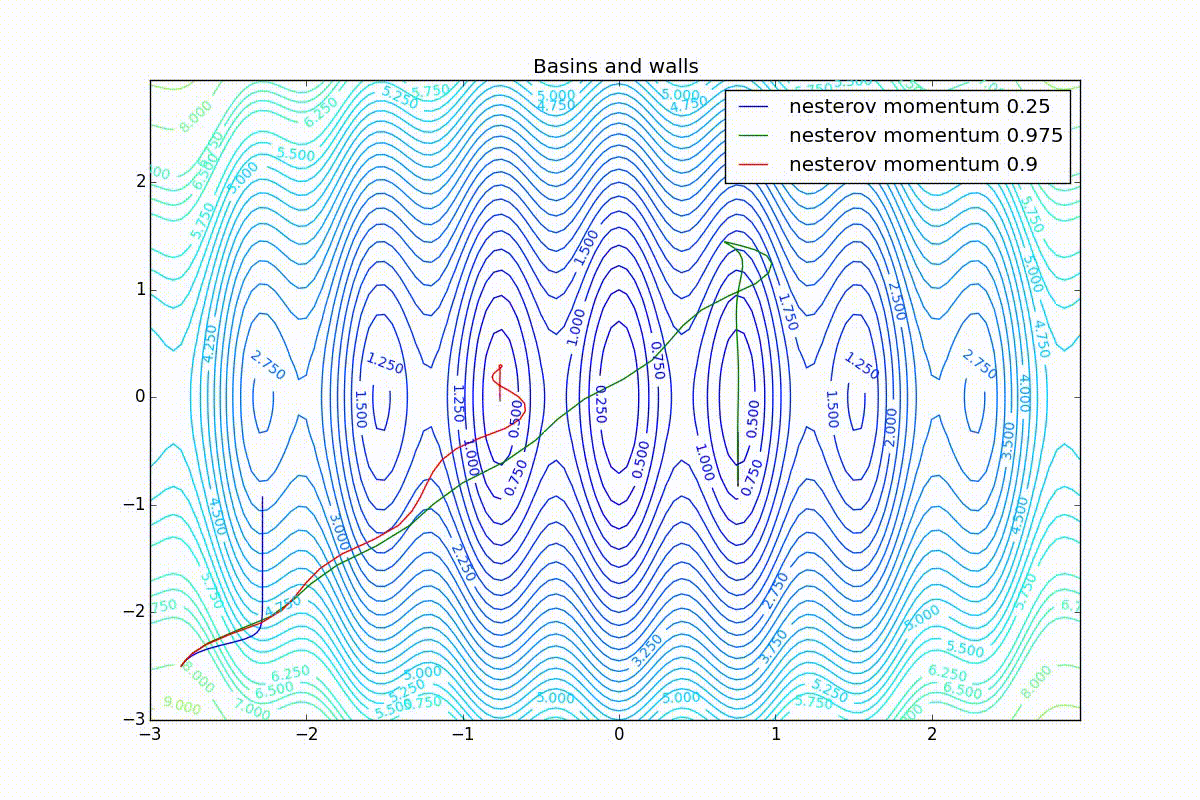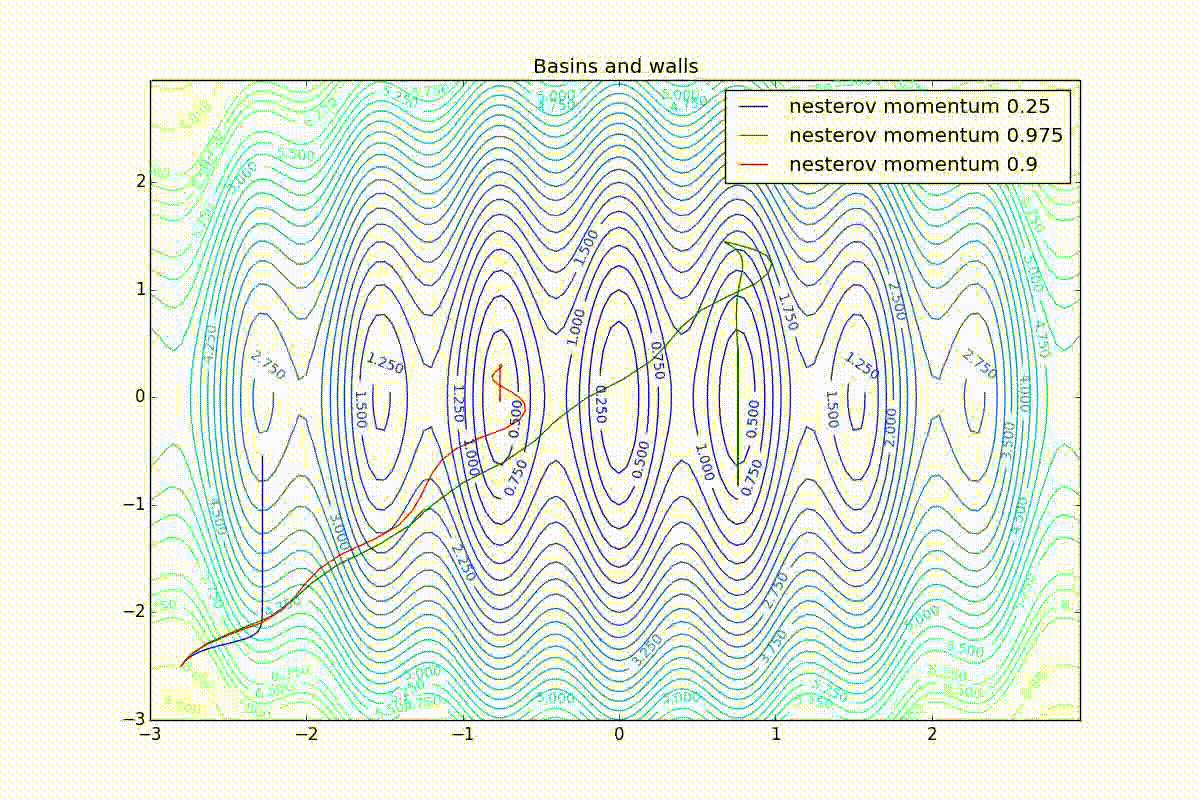
Теперь рассмотрим разные алгоритмы, запущенные из одной точки.

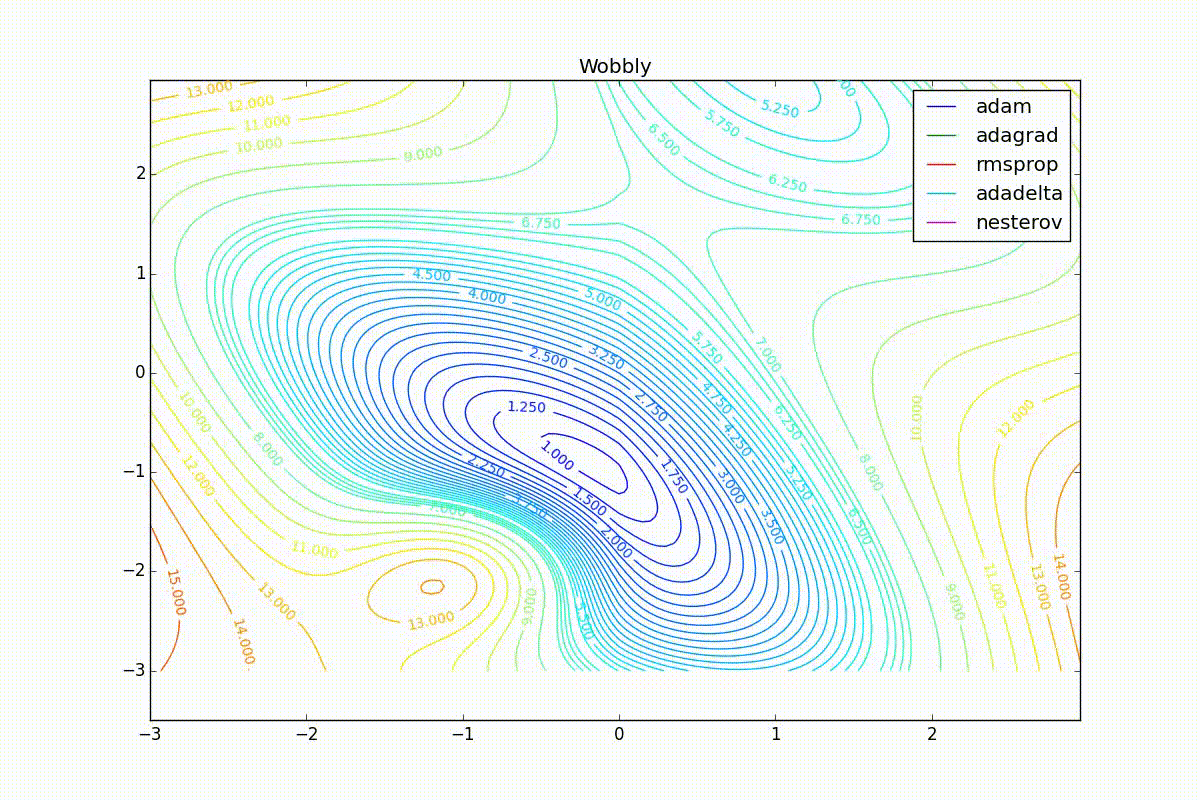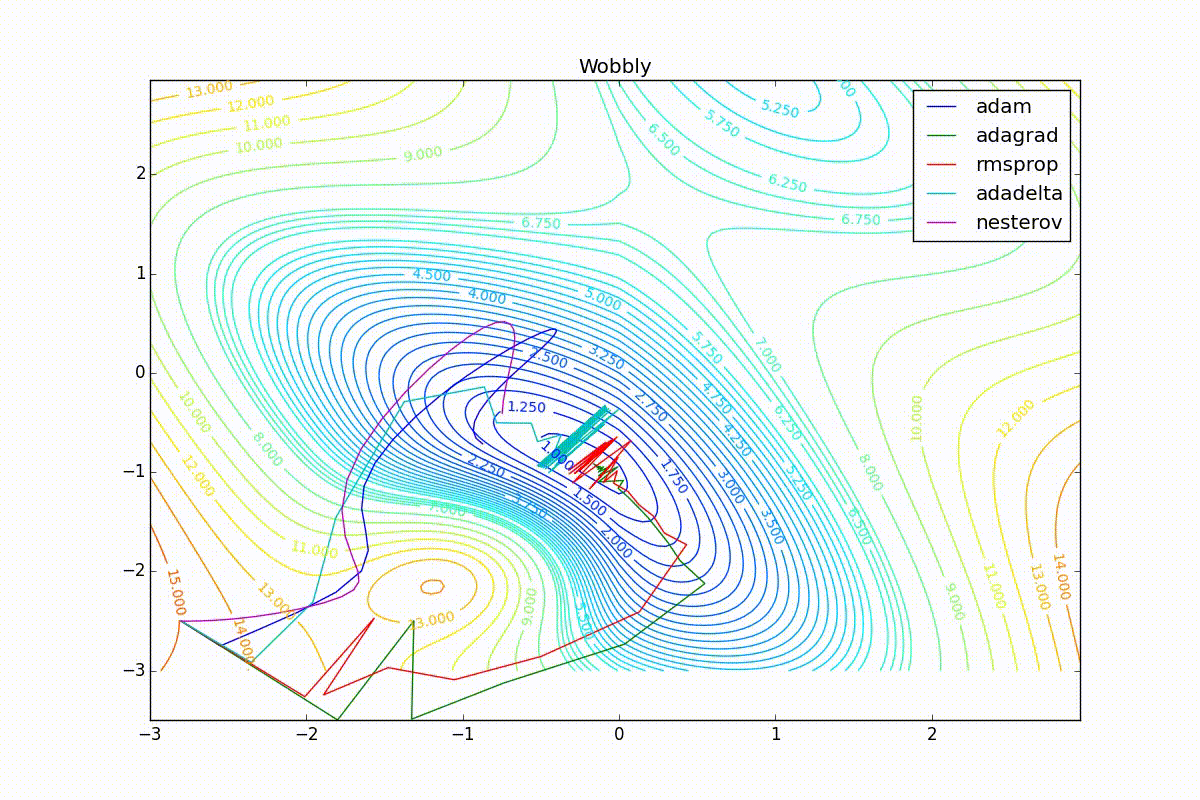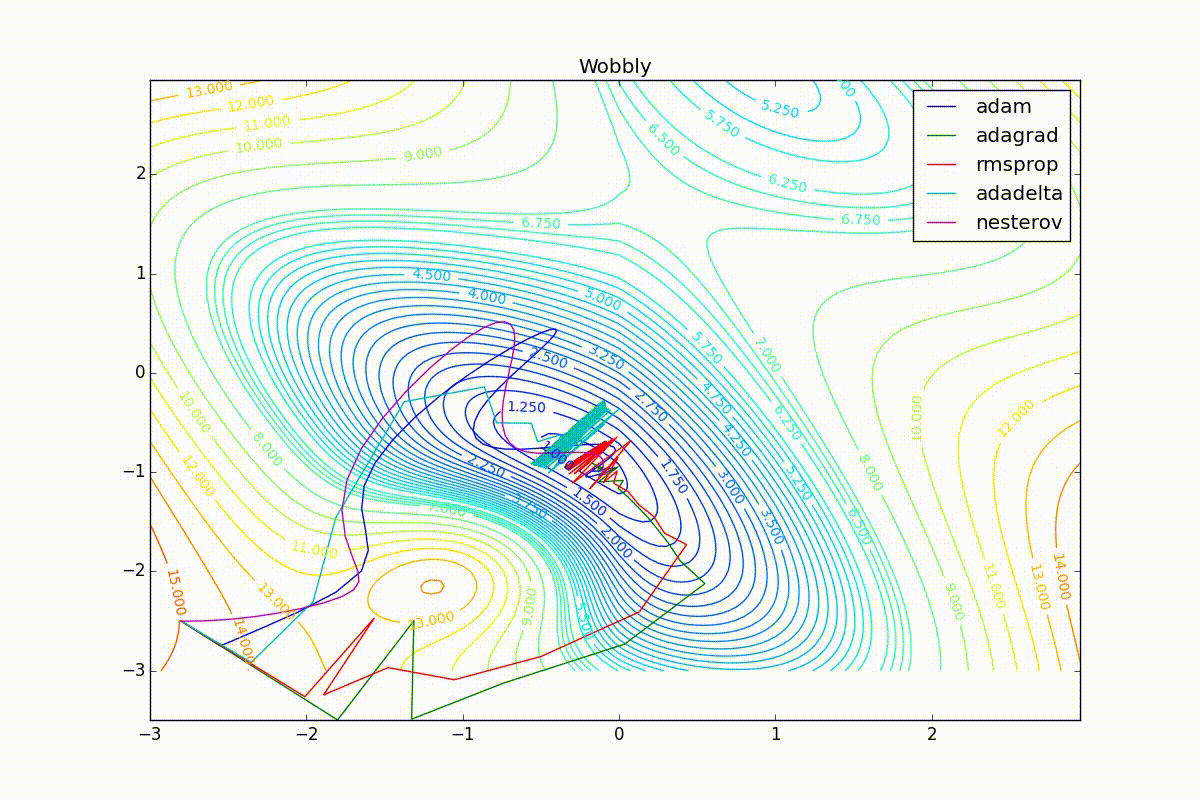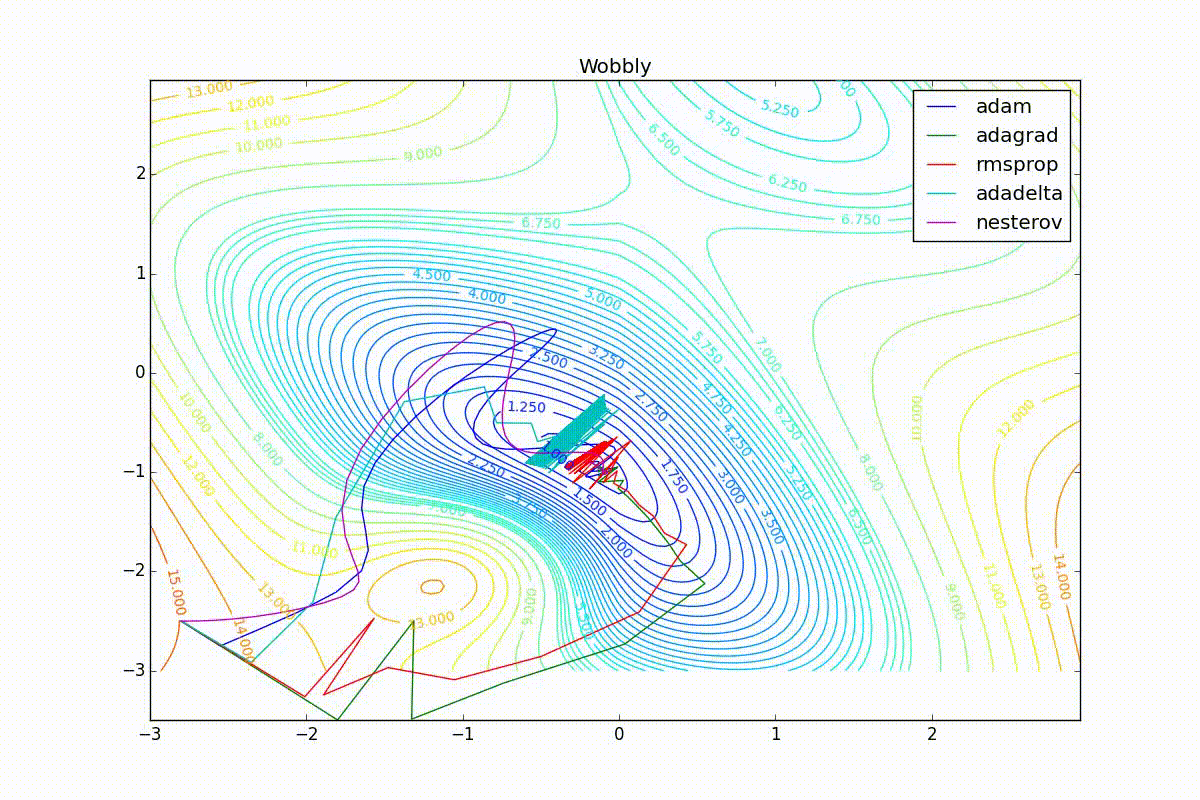
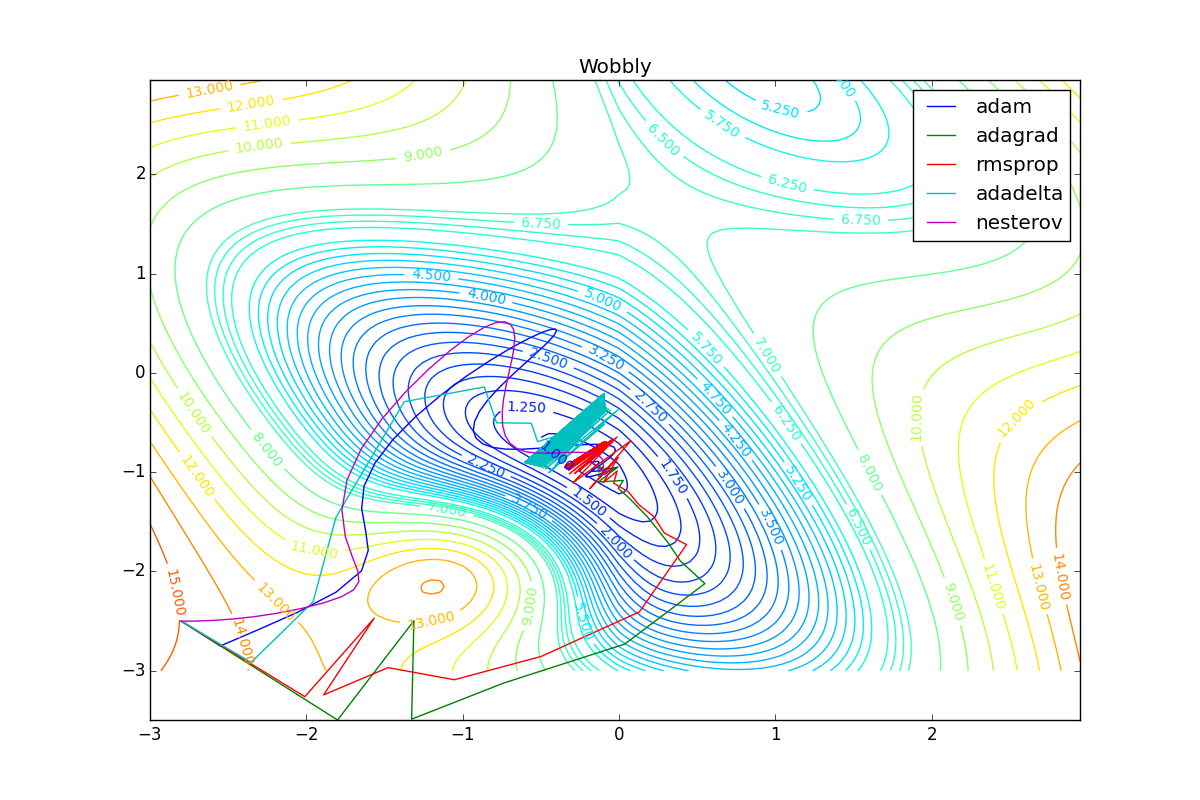
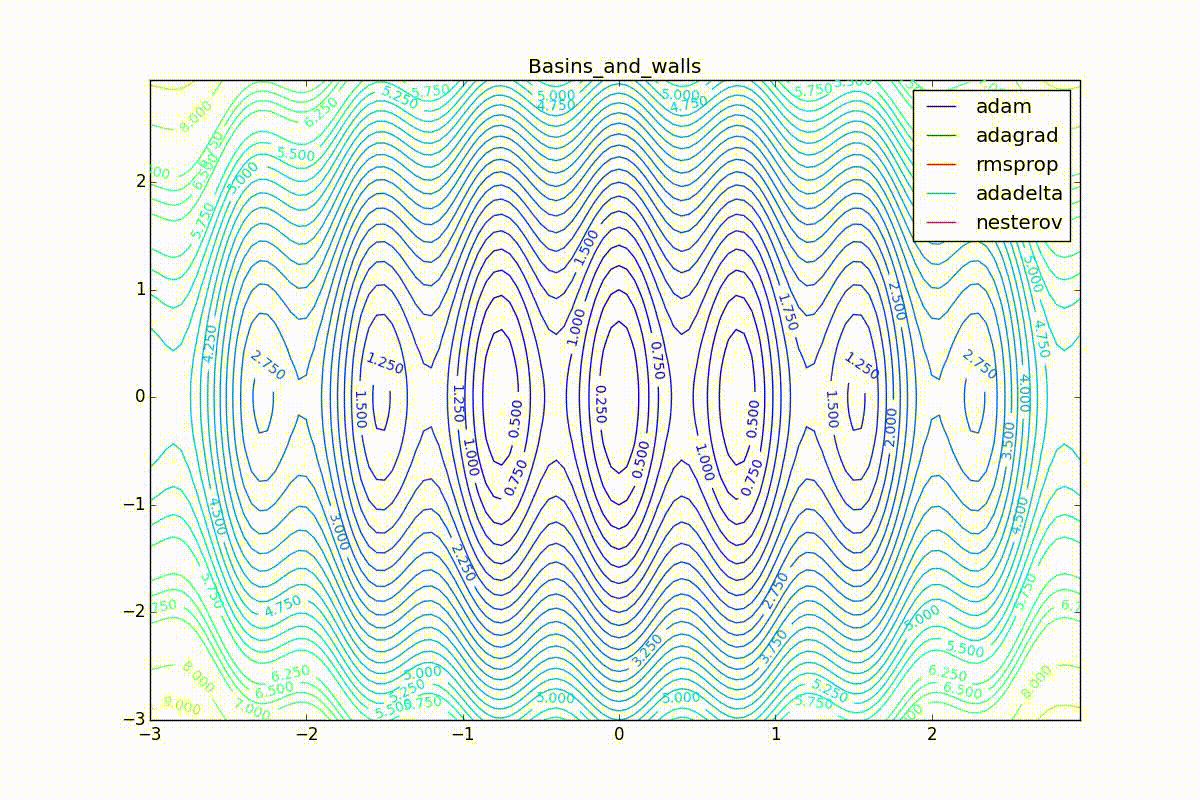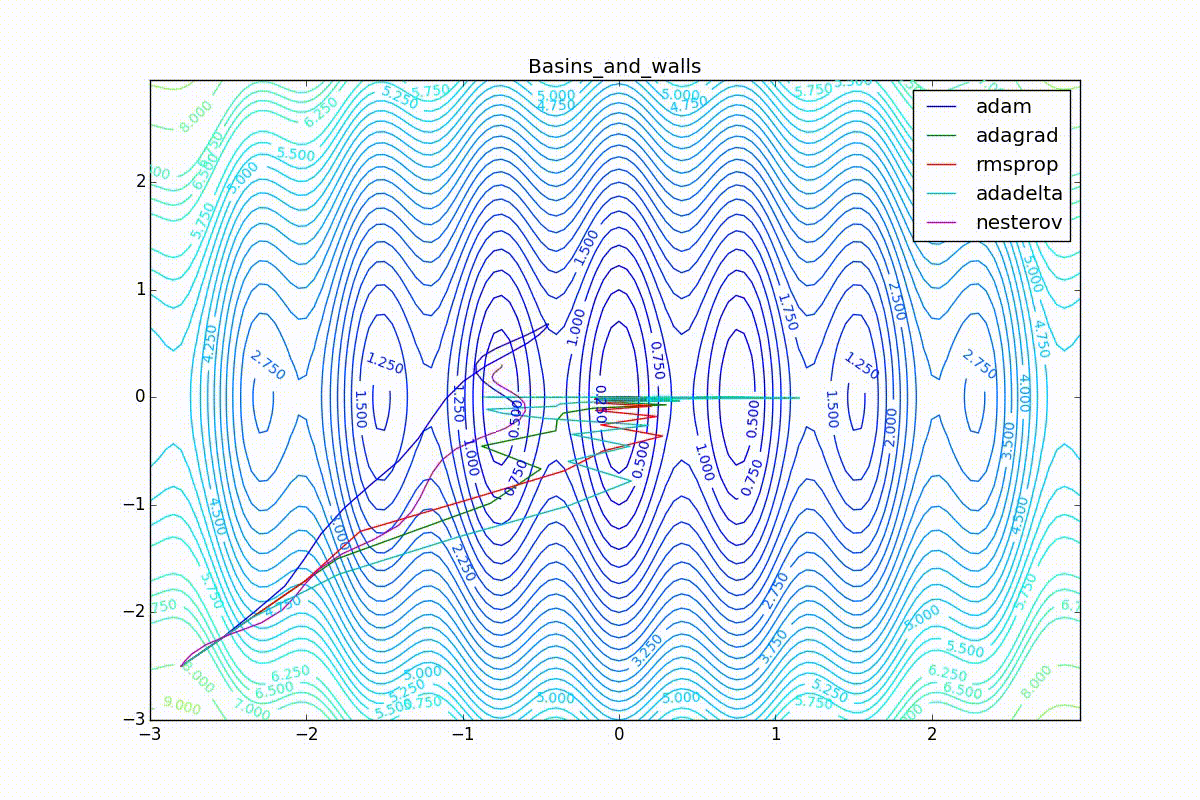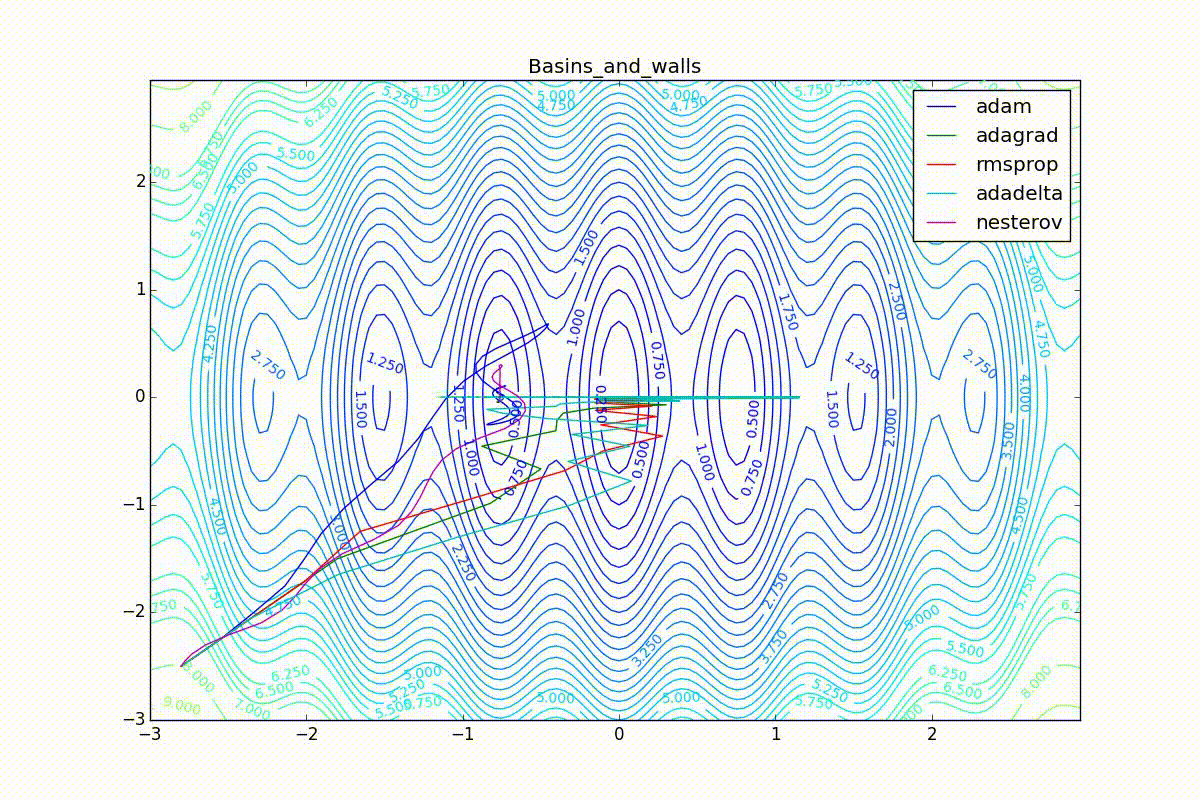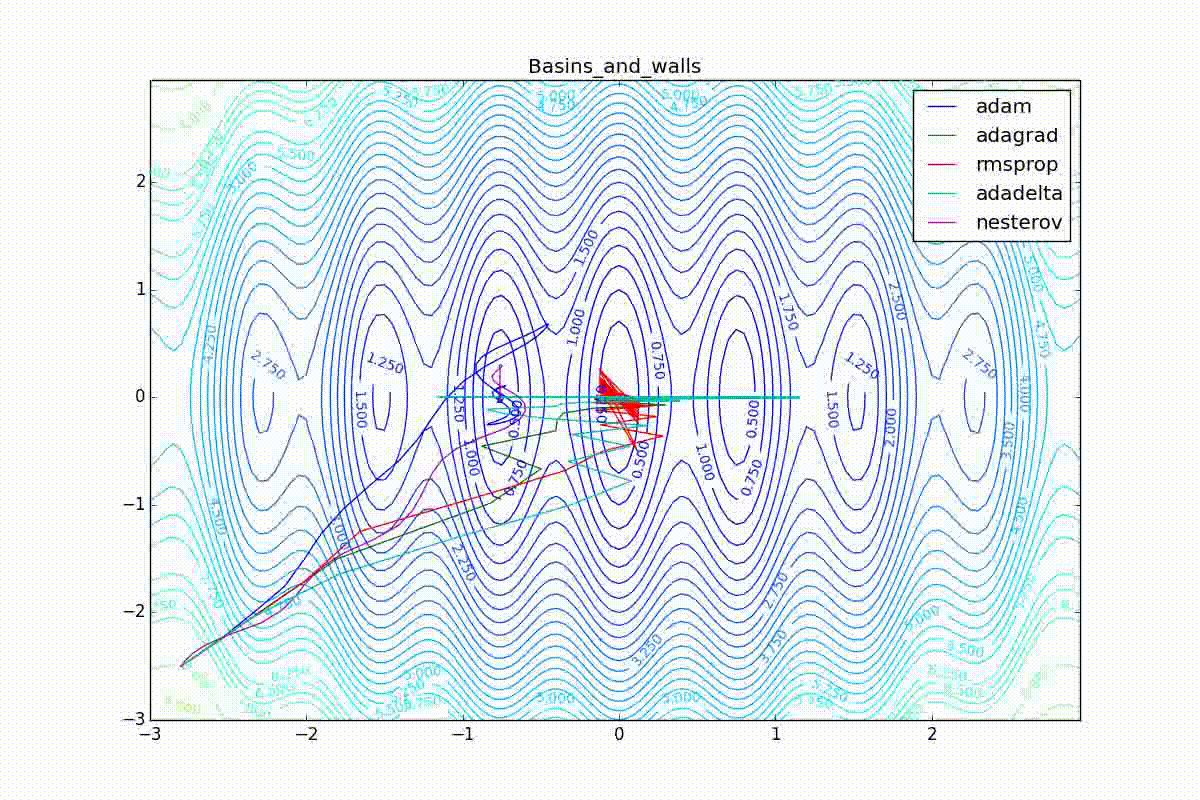
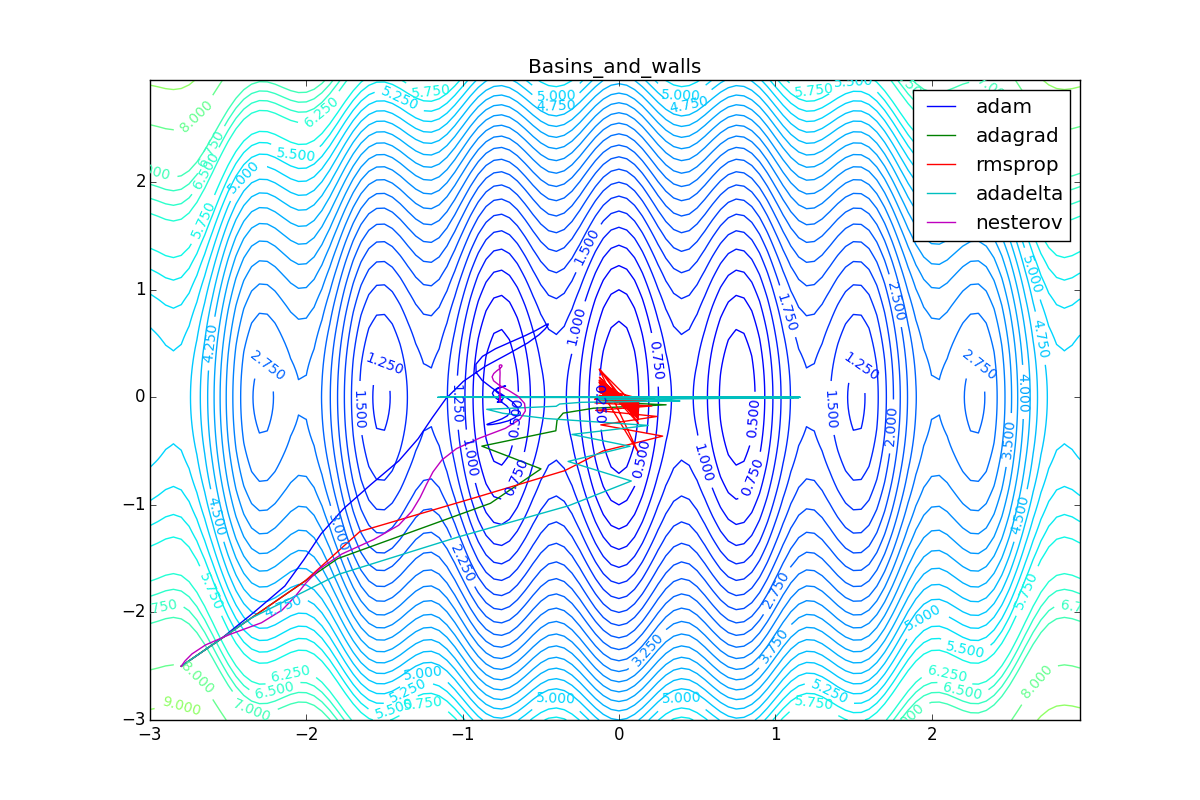
Как видно, все они довольно хорошо сходятся (с минимальным подбором скорости обучения). Обратите внимание на то, какие большие шаги совершают Adam и RMSProp в начале обучения. Так происходит потому что с самого начала не было ниаких изменений ни по одному параметру (ни по одной координате) и суммы в знаменателях (14) и (23) равны нулю. Вот тут ситуация посложнее:

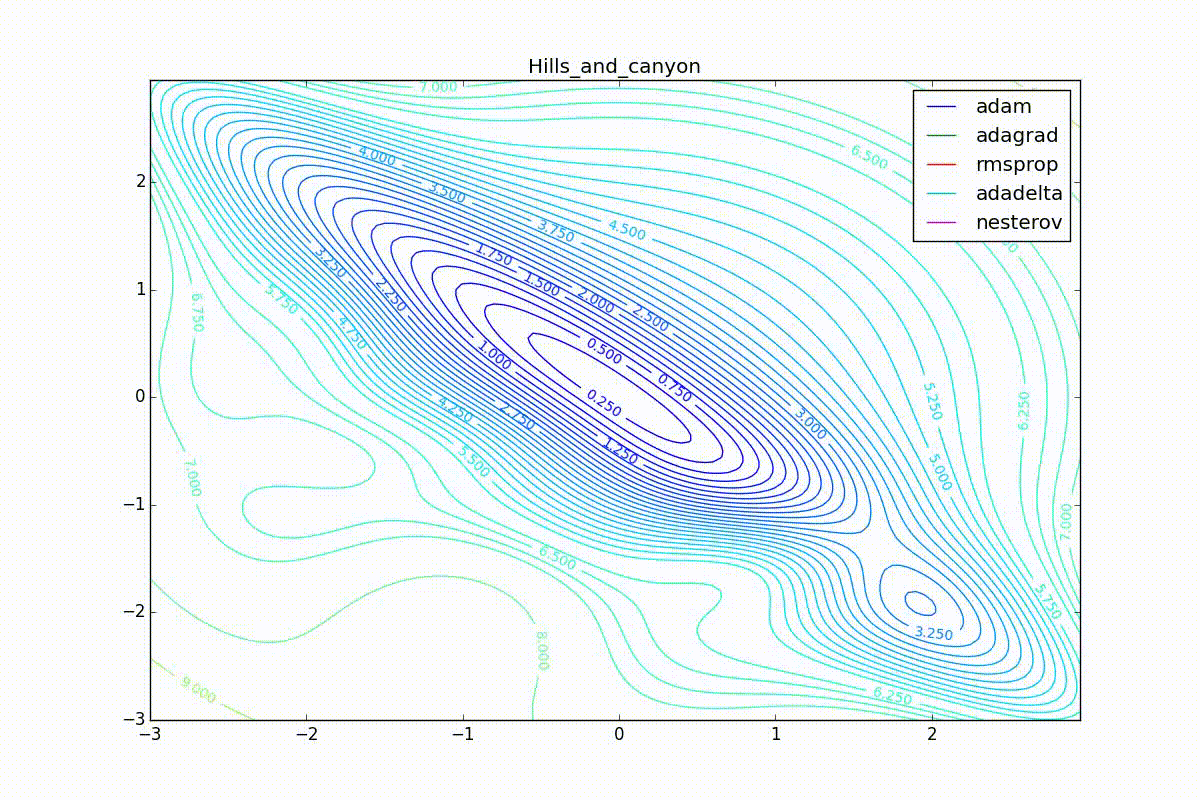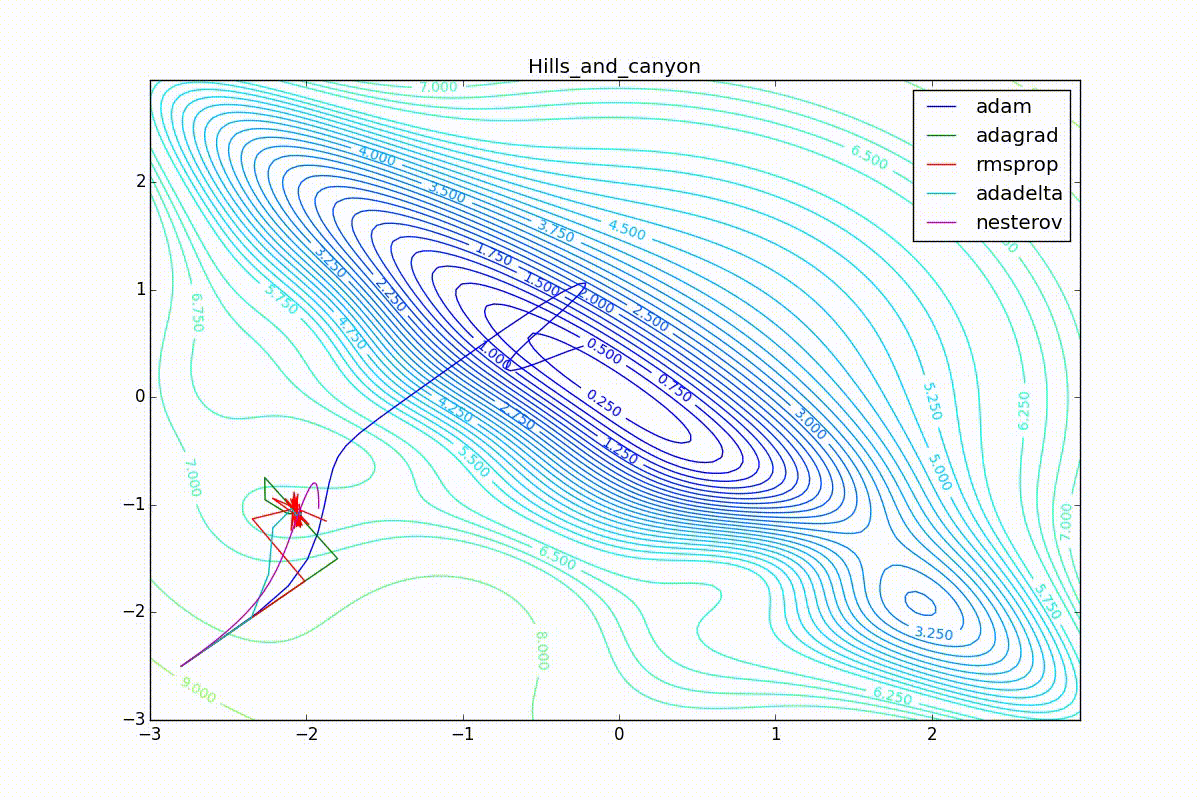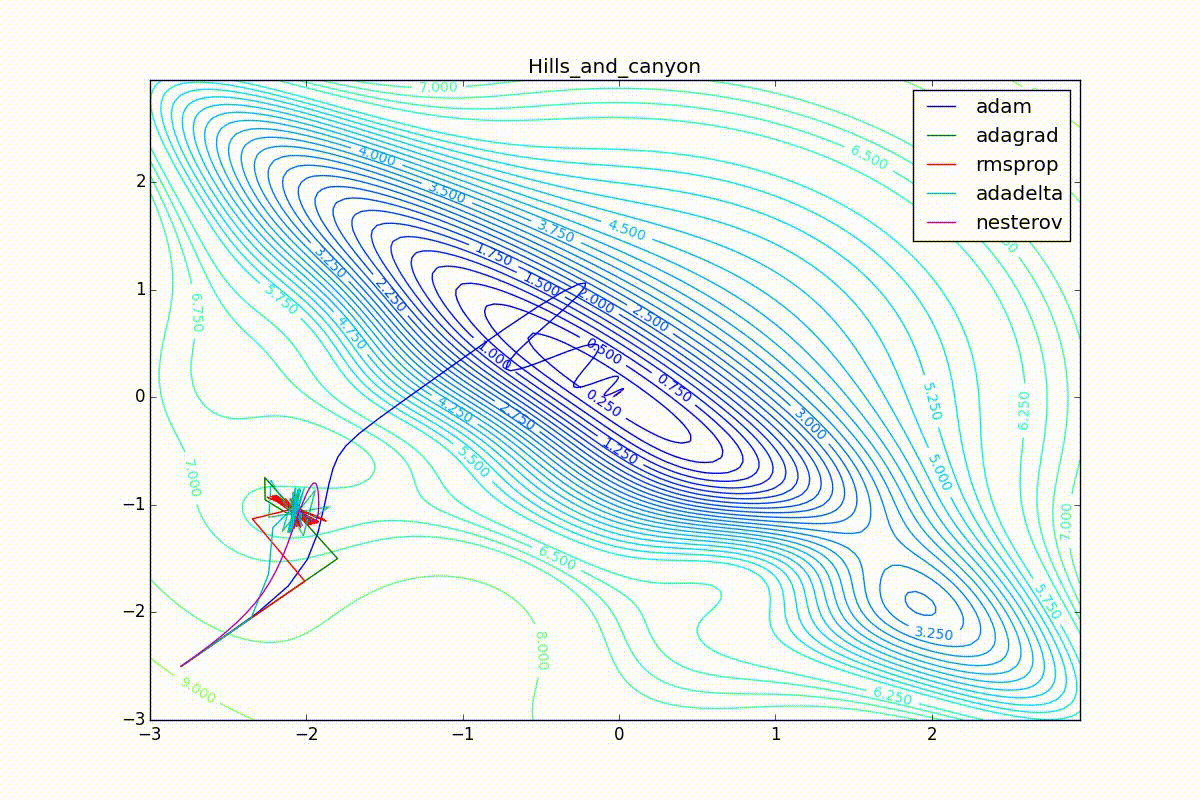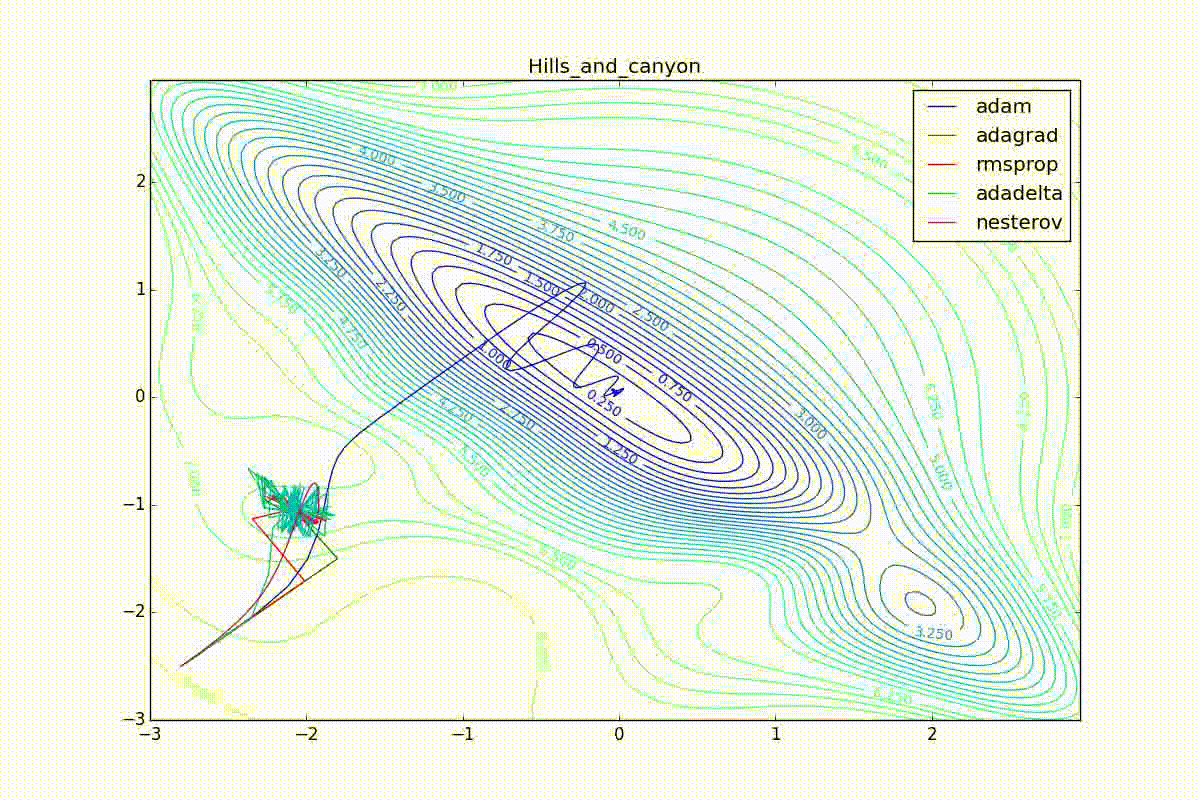
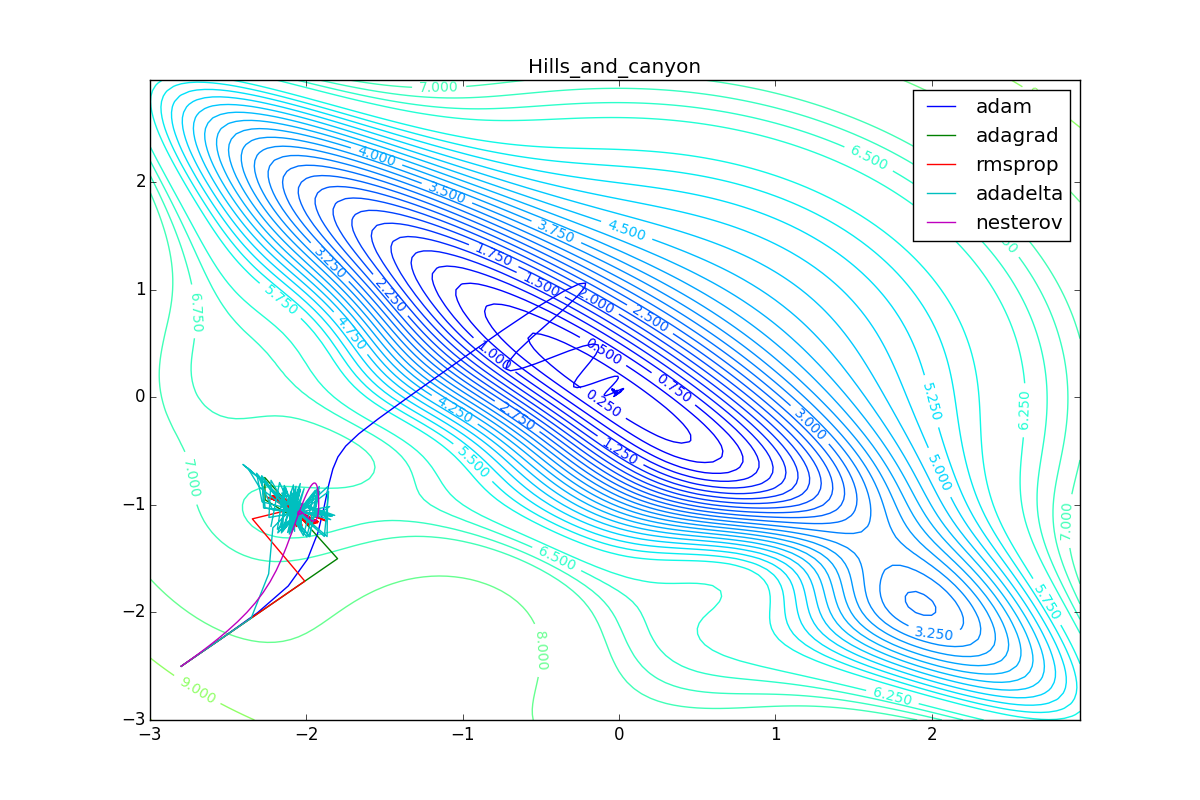
Кроме Adam, все оказались заперты в локальном минимуме. Сравните поведение метода Нестерова и, скажем, RMSProp на этих графиках. Ускоренный градиент Нестерова, с любым $\inline \gamma$ , попав в локальный минимум, некоторое время кружится вокруг, затем теряет импульс и затухает в какой-нибдуь точке. RMSProp же рисует характерных «ёжиков». Это тоже связано с суммой в знаменателе (14) — в ловушке квадраты градиента маленькие и знаменатель снова становится маленьким. На величину скачков влияют ещё, очевидно, скорость обучения (чем больше $\inline \eta$ , тем больше скачки) и $\inline \epsilon$ (чем меньше, тем больше). Adagrad такого поведения не показывает, так как у этого алгоритма сумма по всей истории градиентов, а не по окну. Обычно это желательное поведение, оно позволяет выскакивать из ловушек, но изредка таким образом алгоритм сбегает из глобального минимума, что опять-таки, ведёт к невосполнимому ухудшению работы алгоритма на тренировочной выборке.

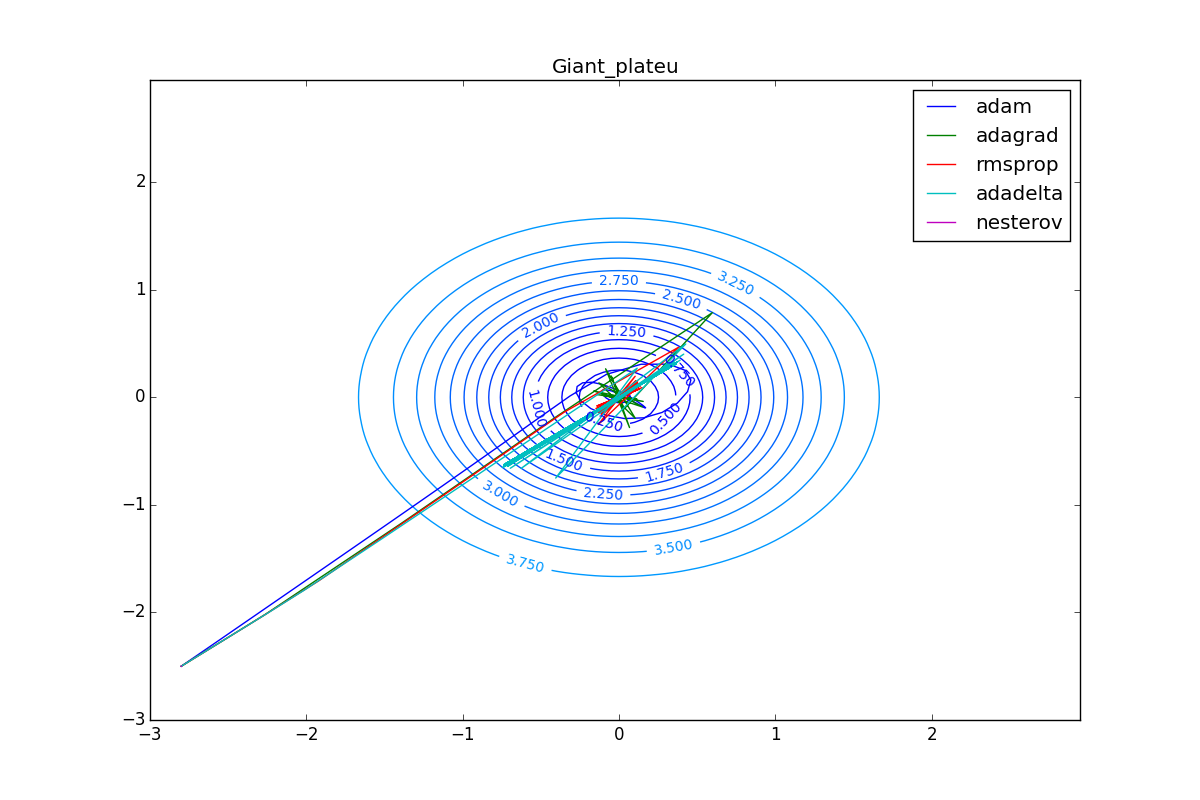
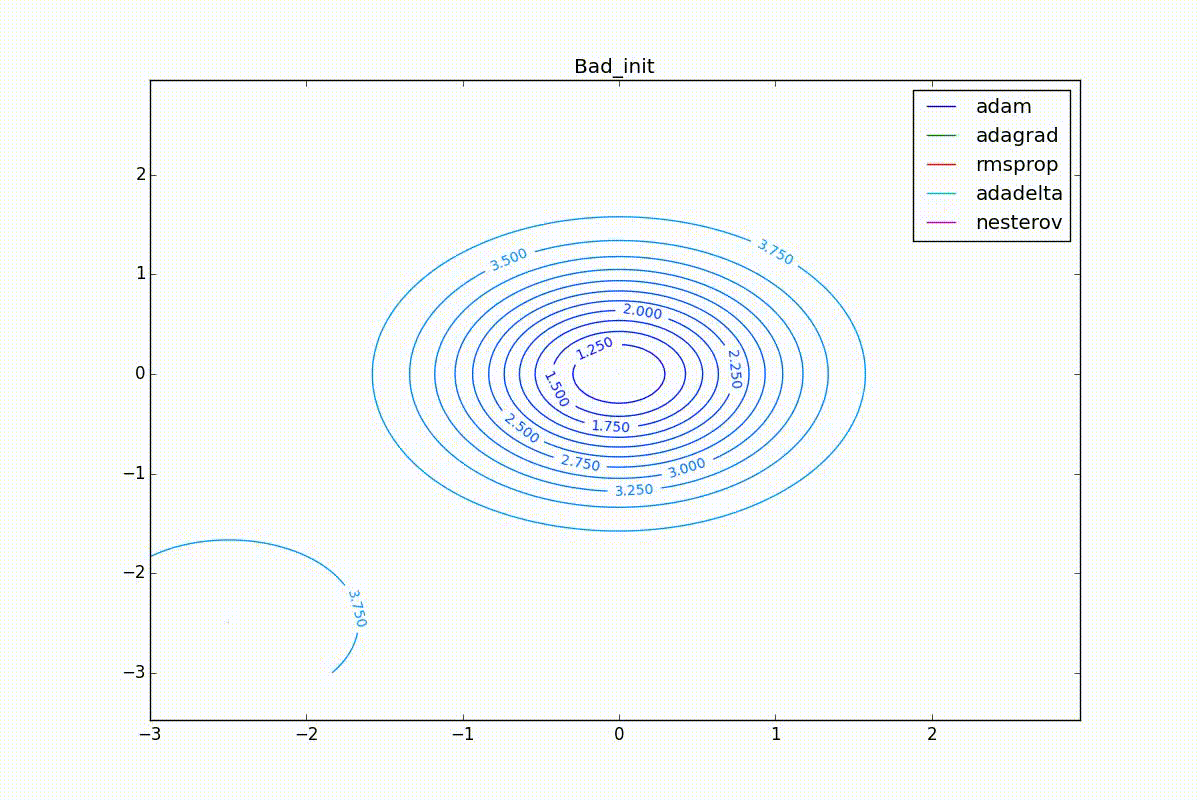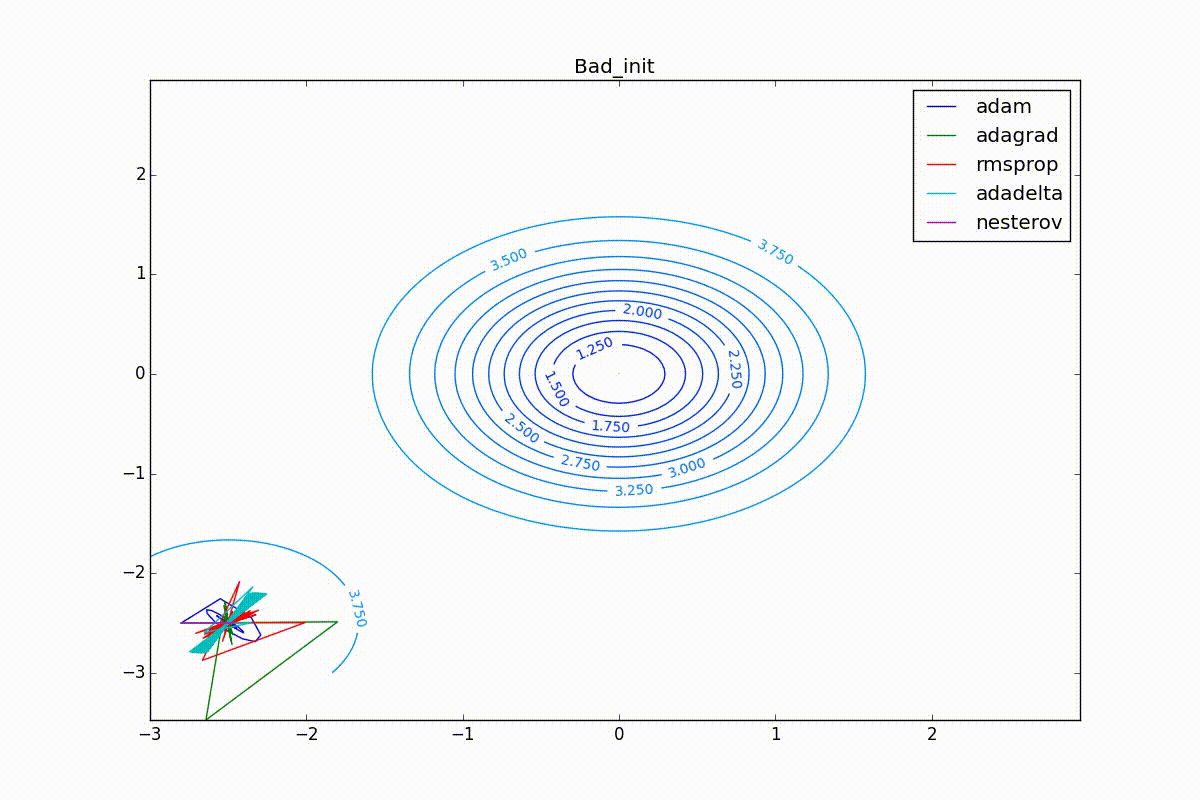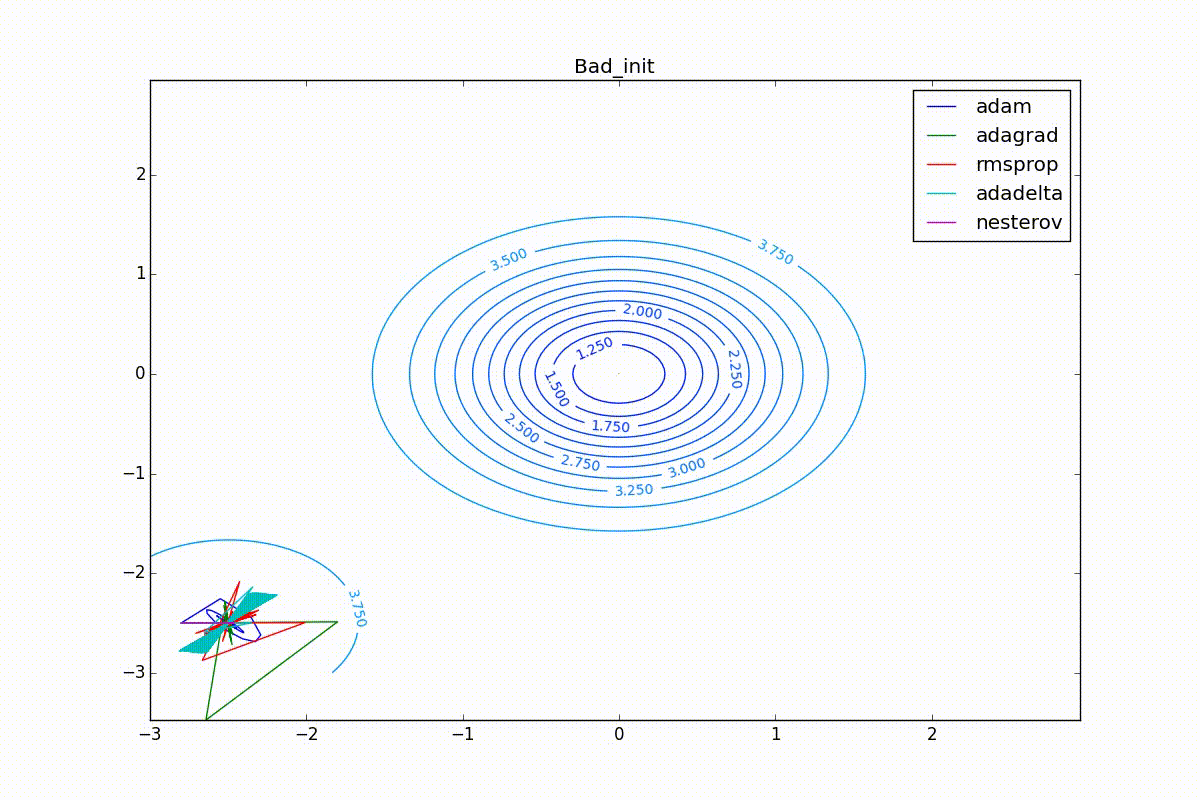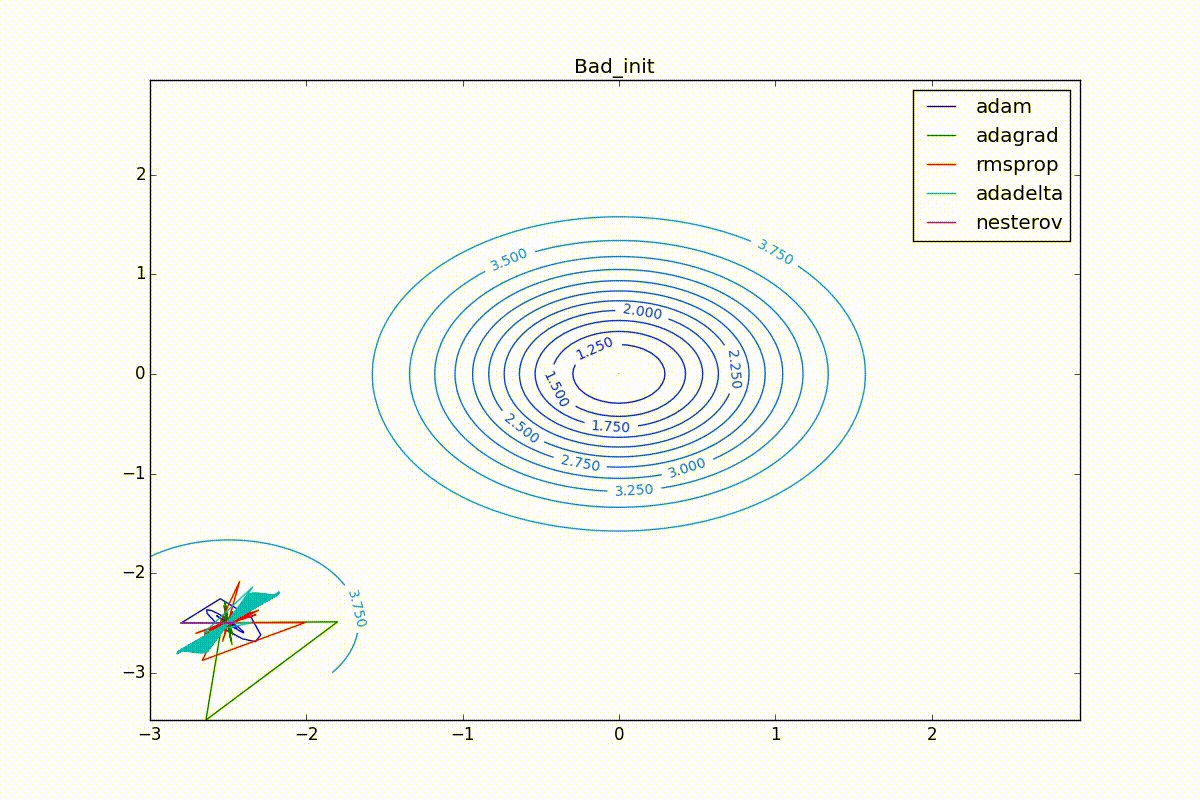
Наконец, заметьте, что хоть все эти оптимизаторы и могут найти путь к минимуму даже по плато с очень маленьким уклоном или сбежать из локального минимума, если до этого они уже набрали импульс, плохая начальная точка не оставляет им шансов:

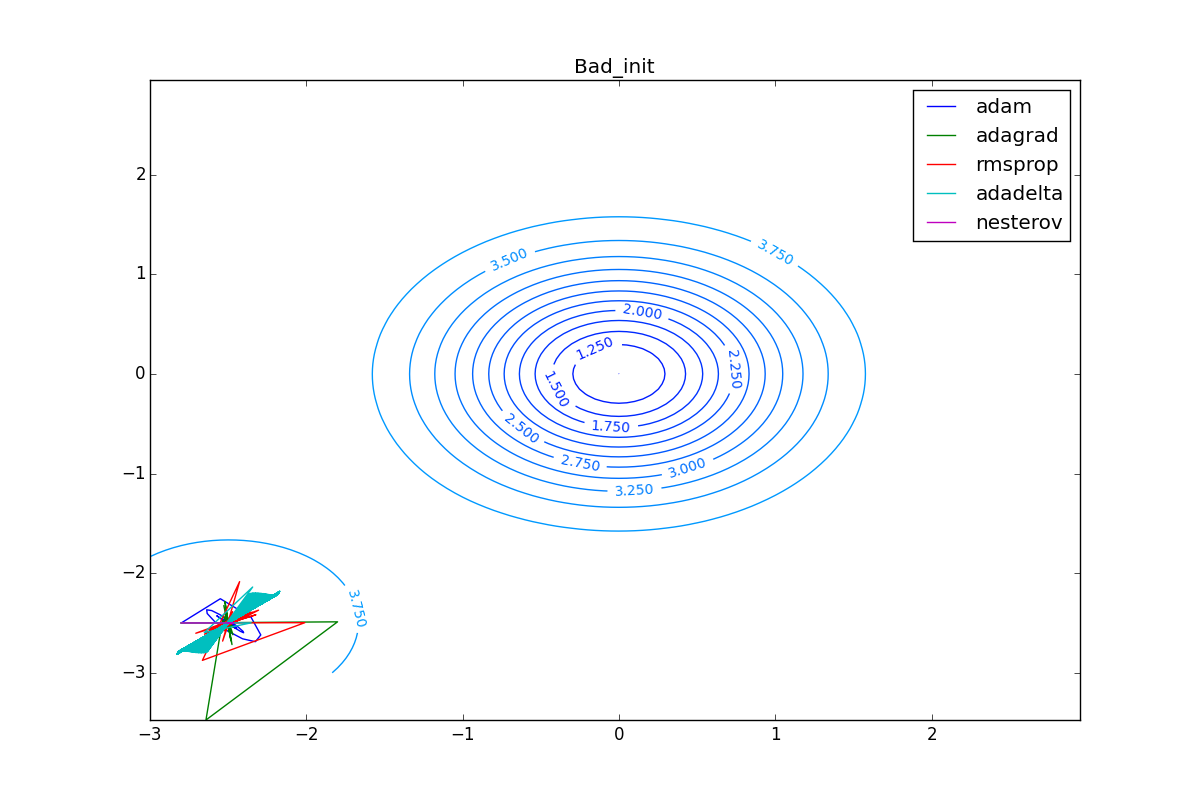
Заключение

Итак, мы рассмотрели несколько наиболее популярных оптимизаторов нейронных сетей первого порядка. Надеюсь, эти алгоритмы перестали казаться волшебным чёрным ящиком с кучей загадочных параметров, и теперь вы можете принять взвешенное решение, какой из оптимизаторов использовать в своих задачах.

Напоследок, всё же уточню один важный момент: вряд ли смена алгоритма обновления весов одним вжухом решит все ваши проблемы с нейронной сетью. Конечно прирост при переходе от SGD к чему-то другому будет очевиден, но скорее всего история обучения для алгоритмов, описанных в статье, для сравнительно простых датасетов и структур сети будет выглядеть как-то так:

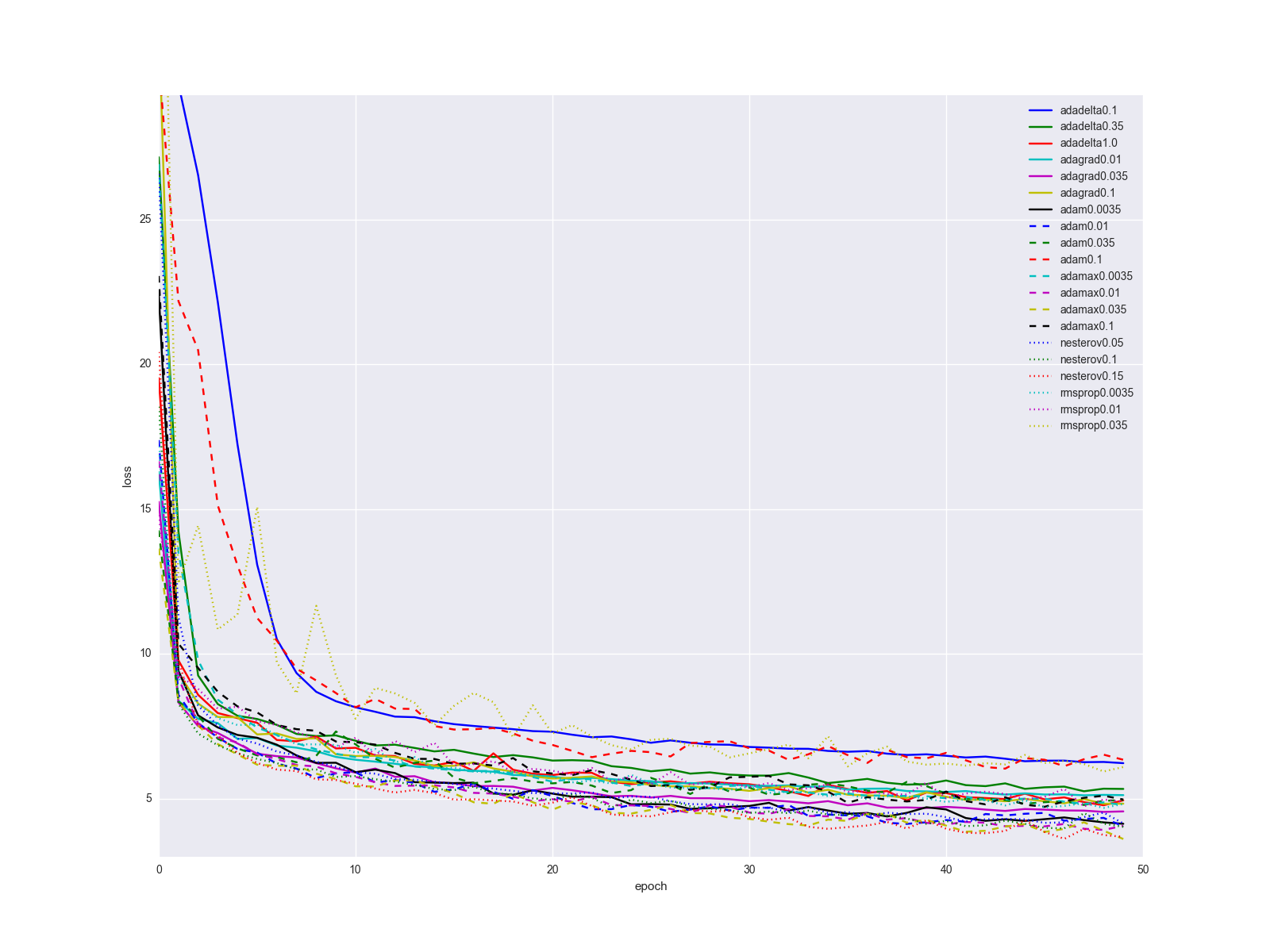
… не слишком впечатляет. Я бы предложил держать качестве «золотого молотка» Adam, так как он выдаёт наилучшие результаты при минимальном подгоне параметров. Когда сеть уже более-менее отлажена, попробуйте метод Нестерова с разными параметрами. Иногда с помощью него можно добиться лучших результатов, но он сравнительно чувствителен к изменениям в сети. Плюс-минус пара слоёв и нужно искать новый оптимальный learning rate. Рассматривайте остальные алгоритмы и их параметры как ещё несколько ручек и тумблеров, которые можно подёргать в каких-то специальных случаях.

Если хотите несколько собственных графиков с градиентами, воспользуйтесь этим скриптом на питоне (требуется python > 3.4, numpy и matplotlib):

Код

from matplotlib import pyplot as plt
import numpy as np
from math import ceil, floor

def linear_interpolation(X, idx):
    idx_min = floor(idx)
    idx_max = ceil(idx)
    if idx_min == idx_max or idx_max >= len(X
    
            © Habrahabr.ru


    


    

        

        
            


            
                О
                        проекте
                Архив
                
                Реклама
                    Партнёры
                    Правовая информация
                    Контакты
                    Обратная
                        связь