Как быстрее всего сфоткать 35 билбордов в Москве13.04.2017 18:03

Идеи, чем заняться на выходных, ITшники черпают из сотни разных источников. Я, к примеру, недавно увидел конкурс Открытого чемпионата школ по Экономике, заключающегося в том, чтобы сфотографировать максимальное число билбордов Чемпионата. Адреса организаторы любезно предоставили. И несмотря на то, что приз взрослому там не светит (это школьный конкурс), тем не менее крайне интересно было бы узнать, за какое минимальное время можно решить такую задачу.

90f2aae201004f00a2cff411368b1a88.png

Итак, что мы имеем?


3 часа на выходных, 35 адресов билбордов в виде достаточно спорно вбитых адресов (почему-то реестр УНОМ достаточно плохо бьётся с привычными картами), 1 Jupyter с готовым к работе вторым (извините) питоном и множество API различных сервисов.

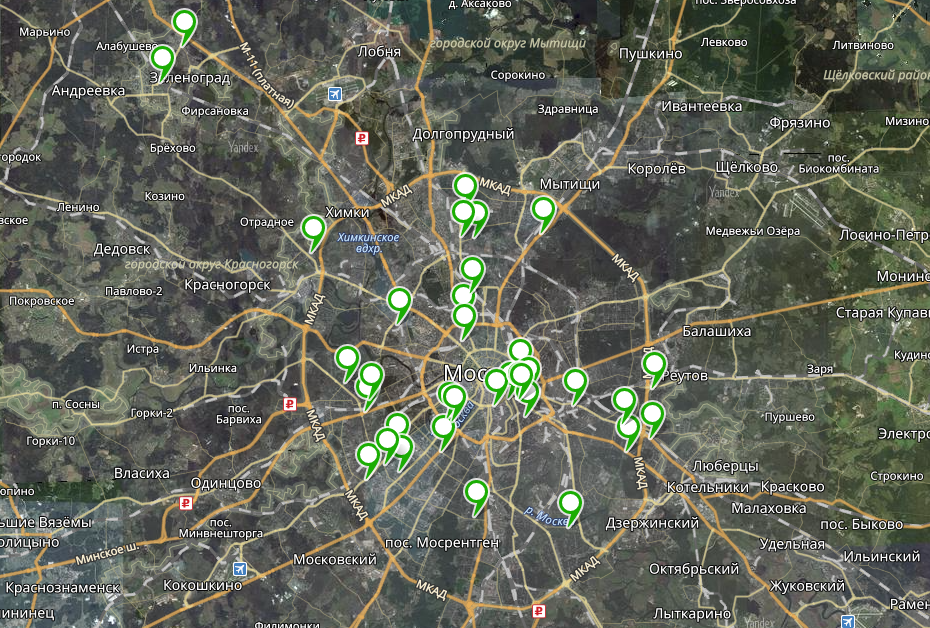
Для начала удобно было бы представить масштаб бедствия на карте. Можно было бы воспользоваться чем-то автоматическим, но 35 адресов быстрее вручную перебить в Конструктор Яндекс.Карт, он сам приведет их к координате. В итоге получилась картинка из ката, из которой стало понятно, что

  • Три точки расположены в Зеленограде и Химках, они явно увеличат время в пути
  • Мало билбордов в центре города
  • Точки расположены достаточно хаотично, и вручную построить хороший маршрут, их соединяющий, едва ли получится

Собственно всего вариантов продолжить такой маршрут $10!=1.03e^{40}$, что примерно сопоставимо с числом уникальных шахматных позиций на доске. Так что надо немного разобраться в достижениях народного хозяйства в области P — NP задач.

Сбор матрицы времени между точками


Становится ясно, что наша задача является примером классической задачи коммивояжёра (TSP). Для того, чтобы её решить (приблеженно), нам нужно построить матрицу расстояний (в нашем случае времен) между каждой точкой. Для решения такой задачи воспользуемся Google Maps API, а именно безумно простой и понятной библиотечкой googlemaps. Работа с этой библиотечкой проста и элегантна, получить время между двумя точками на карте можно настолько просто: 
import googlemaps
import datetime

gmaps = googlemaps.Client(key='AIxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx')
resp = gmaps.directions(
    origin='55.71802 37.573753',
    destination='55.73481 37.66521',
    mode='driving', # Либо 'transit' для общественного транспорта
    region='ru',
    language='en',
    departure_time=datetime.datetime.now(), 
)
distance_time = resp[0]['legs'][0]['duration_in_traffic']['value'] # Для авто
print resp[0]['legs'][0]['duration_in_traffic']
# Out[]: {u'text': u'49 mins', u'value': 2917}

Итак, осталось заполнить матрицу 36×36 всех расстояний. Заметьте, что добраться от точки A→B занимает НЕ столько же времени, сколько из B→A, поэтому сократить работу в два раза не получится (хотя диагональ конечно же заполнена нулями). Можно было бы просто пройтись по заранее созданной пустой матрице и заполнить её, однако мне больше нравится подход, когда я сначала храню все элементы матрицы в виде списка [[x,y,value]], а потом делаю .pivot, «разворачивая» матрицу.
distances = []
for origin,destination in permutations(points['lat lng'], 2):
    resp = gmaps.directions(
        origin=origin,
        destination=destination,
        mode='driving',
        region='ru',
        language='en',
        departure_time=now,
    )
    distance_time = resp[0]['legs'][0]['duration_in_traffic']['value'] # Для авто
    distances.append(
        [origin,destination,distance_time]
    )

distances = pd.DataFrame(distances, columns='origin,destination,distance_time'.split(','))
distances_matrix = distances.pivot_table(
    index='origin', columns='destination', 
    values='distance_time'
).fillna(0)

Тут можно сразу отметить, что я большой фанат Pandas Dataframes, и с ними жизнь становится лучше. Если не слышали, обязательно почитайте, вам понравится. Ну и, конечно, как хорошо писать на Питоне, в котором уже есть готова чудесная функция itertools.permutations, возвращающая все пары (тройки, четверки, что нужно) элементов заданного списка. Нет костылям!

Итоговая матрица получилась примерно такой:

c6305f493a6246558e8fe5702c395439.png

Кстати, тут ещё сразу можно изучить, а насколько вообще близки друг к другу наши точки? Иными словами, посмотреть на распределение времени в пути между всеми точками:

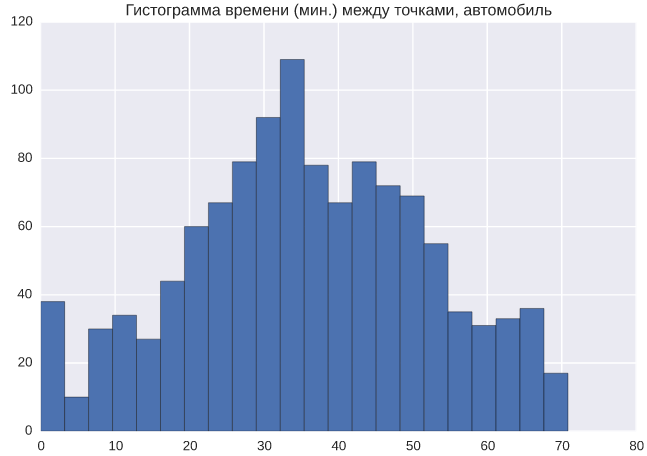
b701170c266c4d789cba4eb2830d95b4.png

Хотя в целом всё довольно ожидаемо. Много точек очень близко, распределение достаточно «нормальное», всё из-за того, что на машине ты можешь двигаться в любую сторону. Забегая немного вперед, вот то же распределение, только для общественного транспорта:
0f5a3a20d3e14974b27a404ff0fb0c99.png

Совсем другая картинка: распределение намного более «вытянуто» вправо, то есть есть относительно мало точек, между которыми может быстро (быстрее 40 минут) переместиться на общественном транспорте. Ну и естественно, что время на транспорте в целом больше (более или менее в два раза).

TSP


Итак, теперь по матрице необходимо построить оптимальный маршрут. Надо сказать, что эта задача уже достаточно хорошо изучена, к примеру, есть очень хорошая гугловая библиотека ortools, позволяющая перебирать маршруты на тысячах и десятках тысяч точек.

Однако в нашем случае всего десятка точек необходимости в сложных алгоритмах нет. Можно воспользоваться жадным алгоритмом двойного прохода, и получить результат почти не отличающийся от «канонического».

Итак, алгоритм будет таким:

1. Инициируем начальную и финальные точки.
2. Берем две точки с наименьшими расстояниями от инициированных, добавляем их в маршрут.
3. Посторяем до тех пор, пока не наберем полный маршрут.

Здесь очевидно, что алгоритм очень зависим от выбранных начальных точек (и в целом от порядка точек), поэтому есть довольно простой способ избежать локальных оптимумов: несколько раз «перемешать» точки и посторить работу жадного алгоритма.

Программное реализацию этого алгоритма я позаимствовал из библиотеки библиотеку Дмитрия Шинякова.

Библиотека на вход принимает numpy квадратную матрицу, на выход выдаёт path: массив индексов точек в порядке по маршруту. Интересно, что Google Maps не позволяют строить маршруты с более чем 23 промежуточными точками, поэтому «на одной карте» построить маршрут не удастся. Я пошел на хитрость, и с помощью той же googlemaps просто разбил маршрут на два и построил его.

coords_path = distances_matrix.index[path] # Получаем точки в правильном порядке

# Latitude-longitude pairs
start = map(float, coords_path[0].split(' '))
waypoints = map(lambda p: map(float, p.split()), coords_path[1:24]) #  первые 24 точки
end = map(float, coords_path[24].split())

m = gmaps.Map(height='650px')
ochDirections = gmaps.directions_layer(start, end, waypoints=waypoints)
m.add_layer(ochDirections)


start = map(float, coords_path[24].split(' '))
waypoints = map(lambda p: map(float, p.split()), coords_path[25:-1])
end = map(float, coords_path[-1].split())
ochDirections = gmaps.directions_layer(start, end, waypoints=waypoints)
m.add_layer(ochDirections)
m

То же самое можно сделать с помощью Яндекс.Карт, уже без разбивания на два куска. 
base_yandex = 'https://yandex.ru/maps/213/moscow/?ll=37.519600%2C55.819741&z=10&mode=routes&rtext={rtext}&rtt=mt&rtm=atm'
rtext = '~'.join(i.replace(' ', '%2C') for i in coords_path)
print base_yandex.format(rtext=rtext)

Весь код я выложил к себе на гитхаб в виде jupyter notebook’а, чтобы можно было быстро попробовать сделать что-то аналогичное.

Получившийся результат


Итак, в итоге алгоритм выдал оценку времени в 8 часов (без пробок 6 часов). В этот момент захотелось выйти из зоны комфорта милого онлайна, и реально проехаться и сфотографировать все билборды. Дело за малым: нашлась компания, и мы поехали строго в соответствии с построенным маршрутом.

Финальный путь занял всего 10 часов. С учетом остановок и поиска многих билбордов мне кажется, что «лишние» 25% времени полностью оправданы. Нам удалось проехать все указанные в списке точки, однако нашли лишь 23 из 35 билбордов. При этом интересно, что щитов формата 6×3 мы нашли 19 из 24, а ситибордов всего 4 из 11. Скорее всего это связано с тем, что ситиформаты в целом рекламодателям более привлекательны (потому что они расположены ближе к центру), и поэтому их быстрее снимают. Не исключаю и банальную версию, что билборды в принципе не вешались.

В итоге, как мне кажется, получилась достаточно интересная смесь из простого алгоритма, упрощающего рутину и дающего намного более хороший результат, чем человек, и реального применения его на дорогах Москвы. Детский конкурс Открытого Чемпионата школ по экономике мы не выиграли, но нашли, кажется, на порядок больше билбордов, чем самый активный участник.

Комментарии (5)

  • 13 апреля 2017 в 16:08

    +1

    ↑

    ↓

    А построенный маршрут в каком-либо виде можно увидеть? Было бы неплохо, если бы в «Получившийся результат» была ещё и соответствующая картинка.

    P.S. А выигрывает как обычно человек с большим количеством родственников\знакомых в разных частях города, которые согласятся сделать небольшой крюк к нужному месту.

    • 13 апреля 2017 в 16:30

      +1

      ↑

      ↓

      Итоговый маршрут вот такой на Яндекс.Картах. Ссылка из гитхаб.кода, но картинку добавлю, отличная идея

      • 13 апреля 2017 в 17:23

        0

        ↑

        ↓

        Насколько я помню, классическая задача коммивояжёра включает в себя возврат в исходный город. Не заметил его в вашем маршруте.

    • 13 апреля 2017 в 17:20 (комментарий был изменён)

      0

      ↑

      ↓

      -

      • 13 апреля 2017 в 17:29

        0

        ↑

        ↓

        Всё верно, Гамильтонов путь на графе я не нашёл, а искал незамкнутую цепь, содержащую все точки. А также я был дважды в одной точке (случайно). Тем не менее задаче поиска кратчайшего маршрута между всеми точками без возврата домой свойственны все те же свойства, что и «классической» задаче коммивояжёра.

        Если вернуться к задаче, то я попробовал несколько вариантов решения и пермутаций точек, и финальная оказалась очень близка к дому, хотя это и не было важно: хотелось минимизировать именно время от первой до последней. Время возвращения от последней точки до дома меня вообще не интересовало, в воскресенье вечером возвращаться из Зеленограда в Москву совсем несложно.

        А место моего дома я убрал из анализа из соображений приватности. :-)

© Habrahabr.ru