Геометрия данных 6. Физика и математика03.11.2017 16:03

Это заключительная статья серии о ди- и би-координатах. В размашистом и свободном стиле покажем, как введенные понятия можно использовать для исследования данных. Конкретно обратимся к теории чисел — это хорошее поле для демонстрации идей как математики, так и физики.

Физика — почему пространство-время псевдоевклидово?

Особенность дистанционных координат в том, что лежащее в их основе понятие дистанции (квадрата расстояния) между объектами играет ключевую роль в свойствах окружающего нас мира.

Например, интервал в специальной теории относительности представляется как сумма (и разность) дистанций компонент:

$\Delta s^2 = \Delta x^2 + \Delta y^2 + \Delta z^2 - c^2 \Delta t^2 = d_x + d_y + d_z - d_t\quad(6.1)$

Здесь $\Delta s^2=d$ — это дистанция между двумя событиями в мировом пространстве-времени. Вопрос, который мы попытаемся прояснить, заключается в следующем. Почему знак временной компоненты $d_t=c^2 \Delta t^2$ в формуле (6.1) противоположен знакам пространственных интервалов ( $\Delta x^2$ и пр.)? Другая его формулировка — почему окружающее нас пространство-время псевдоевклидово?…

Одно из возможных «объяснений» состоит в том, что временная координата является мнимой: $ict$ . Возведение мнимого числа в квадрат дает минус в формуле (6.1). Очевидно, что такое объяснение просто подменяет одно малопонятное (время) другим еще менее понятным (мнимость).

Тем не менее кое-что о свойствах времени можно понять, рассмотрев свойства дистанции в пространстве (внезапно) целых чисел. Но вначале уточним определение разложения дистанции на компоненты.

Коэффициенты компонент дистанции — это барицентрические координаты

Пусть в неком пространстве задан невырожденный дистанционный метрический тензор (ДМТ) $Dm$ . Согласно определению ДМТ — это просто набор ди-координат (полудистанций) базовых вершин относительно друг друга. Невырожденность ДМТ означает, что детерминант ДМТ отличен от нуля — каждая вершина базиса увеличивает размерность ДМТ.

Рассмотрим теперь точку P, которая принадлежит базовому пространству. Если ее ди-координаты $di_P$ добавить в ДМТ, то тензор станет вырожденным, — его определитель обратится в нуль. Это означает, что ди-координаты данной точки могут быть выражены через ди-координаты базиса (линейное разложение). Коэффициентами данного линейного разложения являются би-координаты точки $bi_P$ :

$di_P = Dm \space bi_P\quad(6.2)$

Разложение (6.2) похоже на линейное разложение векторов, но есть и отличие — наличие скалярной компоненты в координатах. Раскрывая матричное произведение и переходя от полудистанций к дистанциям, получаем:

$d_P = m_{P}^{a} d_0 + D_a b^{a}_{P} \quad(6.2.1, 2.13)$

Здесь $d_P$ — дистанционный вектор точки $P$ , $m_{P}^{a}$ — степень точки в базисе $a$ , $d_0 = 1_a = [1,1,...]$ — вектор единиц, $D_a$ — матрица дистанций базиса, $b_{P}^{a}$ — барицентрические координаты точки. Данная формула уже приводилась во второй статье серии (2.13).

(6.2.1) — это разложение вектора $d_P$ по компонентам базиса. Опуская индекс точки и раскрывая произведение $D_a b^{a}_{P}$ , получаем:

$d = m \space d_0 + b^X d_X + b^Y d_Y + b^Z d_Z + ... \quad(6.3)$

Выражение (6.3) эквивалентно представлению интервала (6.1). Роль интервала $s^2$ играет дистанция $d$ , роль компонент $\Delta X^2$ — дистанции $d_X$ .

Из (6.3) следует, что в общем случае коэффициенты перед компонентами могут быть любыми (в том числе и отрицательными). Единственное требование к коэффициентам $b^X, b^Y,...$ — чтобы их сумма равнялась единице.

Таким образом отрицательный коэффициент в разложении дистанции — это компенсация избыточности положительных. Далее покажем, в какого рода базисах возникает необходимость такой компенсации.

Математика — пространство целых чисел

Каждое целое число можно разложить на произведение простых: $6=2 \cdot 3, 9=3 \cdot 3$ и т.д. Простые числа раскладываются на произведение единицы и себя: $11=11 \cdot 1$ . Матрица разложения первых 11 чисел имеет такой вид:
\begin{array}{c | c c c с c c}
X & 1 & 2 & 3 & 5 & 7 & 11 \\
\hline
1 & 1 \\
2 & 1 & 1 \\
3 & 1 & & 1 \\
4 & 1 & 2 \\
5 & 1 & & & 1 \\
6 & 1 & 1 & 1 \\
7 & 1 & & & & 1 \\
8 & 1 & 3 \\
9 & 1 & & 2 \\
10 & 1 & 1 & & 1 \\
11 & 1 & & & & & 1 \\
\end{array}
Простые числа представлены в колонках матрицы — это компоненты. Все остальные числа — в строках, — это кортежи данных. На пересечении кортежа и компоненты — количество множителей простого числа в заданном. Например, на пересечении 9 и 3 стоит 2 — это означает, что $9 = 3 \cdot 3=3^2$ .

Единица отличается от всех остальных чисел. Она присутствует во всех числах, но в ее разложении нет других чисел.

Матрица $X$ является типичной таблицей данных. Такими данными могли быть, например, количество слов в предложениях, оценки (экспертов) чего-либо и т.д.

Метрика пространства чисел

На основании матрицы данных можно задать дистанции между элементами (здесь элементами являются числа) как сумму квадратов разностей их компонент (евклидова метрика):

$D(a,b) = \sum\limits_{p} (x_p(a) - x_p(b))^2 \quad(6.4)$

Индексом $p$ обозначена компонента разложения. Например, евклидова дистанция между 9-кой и 8-кой будет равна:

$D(8,9)=D(9,8) = (1-1)^2 + (3-0)^2 + (2-0)^2 = 13$ .

Вид дистанционной матрицы для первых 11 чисел

\begin{array}{c | c c c с c c c c c с c}
D & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 \\
\hline
1 & — & 1 & 1 & 4 & 1 & 2 & 1 & 9 & 4 & 2 & 1 \\
2 & 1 & — & 2 & 1 & 2 & 1 & 2 & 4 & 5 & 1 & 2 \\
3 & 1 & 2 & — & 5 & 2 & 1 & 2 & 10 & 1 & 3 & 2 \\
4 & 4 & 1 & 5 & — & 5 & 2 & 5 & 1 & 8 & 2 & 5 \\
5 & 1 & 2 & 2 & 5 & — & 3 & 2 & 10 & 5 & 1 & 2 \\
6 & 2 & 1 & 1 & 2 & 3 & — & 3 & 5 & 2 & 2 & 3 \\
7 & 1 & 2 & 2 & 5 & 2 & 3 & — & 10 & 5 & 3 & 2 \\
8 & 9 & 4 & 10 & 1 & 10 & 5 & 10 & — & 13 & 5 & 10 \\
9 & 4 & 5 & 1 & 8 & 5 & 2 & 5 & 13 & — & 6 & 5 \\
10 & 2 & 1 & 3 & 2 & 1 & 2 & 3 & 5 & 6 & — & 3 \\
11 & 1 & 2 & 2 & 5 & 2 & 3 & 2 & 10 & 5 & 3 & — \\
\end{array}

Элементы матрицы отражают, насколько далеко находятся числа друг от друга в нашем пространстве (8-ка здесь далека от 9-ки).

Разложение дистанции на компоненты

Каждому числу в дистанционной матрице соответствует строка (колонка). Данная строка является дистанционным вектором числа. Компоненты вектора — дистанции от данного числа до других чисел.

Независимыми являются только векторы, соответствующие простым числам (включая вектор единицы). Остальные выражаются через простые линейным образом.

Вывод формулы разложения дистанционного вектора

Дистанции от чисел до единицы равны сумме квадратов их компонент за исключением единичной компоненты:

$D(a,1) = D_{a1} = \sum\limits_{p} (x_p(a) - x_p(1))^2 =\sum\limits_{i\ne1} x_p(a)^2 = \sum\limits_{p} x_p(a)^2 - 1 \quad(6.5)$

Подставляя (6.5) в (6.4) и переходя к тензорной форме записи, получаем:

$D_{ab} = D_{a1} + D_{b1} + 2 - 2G_{ab} \quad(6.6)$

где $G_{ab} = X_{a}^{p}X_{pb} \quad(6.7)$ — матрица Грама (грамиан).

Грамиан составных чисел можно выразить через грамиан простых. Пусть, например, $a$ — это составное число, которое можно разложить на простые $a = b*c$ . Тогда вектор составного числа $x_a$ — это сумма векторов его простых компонент:

$x_a = x_b + x_c - x_1$ , где $x_1 = [1, 0, 0, ...]$ — вектор единицы.

В общем случае, если составное число состоит из $n_a$ простых (не включая единицу), то разложение его вектора будет таким:

$x_a = \sum\limits_{p}x_p - (n_a-1)x_1 \quad(6.8)$

Здесь $x_p$ — вектор простого числа.
Например, разложение 6-ки будет таким:
$x_6=x_2 + x_3 - (2-1)x_1 = [1,1,0,...] + [1,0,1,0,...] - [1,0,0,...] = [1,1,1,0,...]$ .

Разложение (6.8) можно подставить в грамиан (6.7). Рассматривая строки (столбцы) грамиана как векторы, получаем в итоге следующее разложение вектора грамиана составного числа $g_a$ через простые:

$g_a = \sum\limits_{p}g_p + 1 - n_a \quad(6.9)$

Вектор грамиана (6.9) можно подставить в выражение (6.6) и получить искомое выражение для дистанционного вектора:

$d_a = m(a) d_0 - (n(a)-1) d_1 + \sum\limits_{p}d_p \quad(6.10)$

Здесь $d_a$ — дистанционный вектор числа $a$ , дистанции от числа до остальных чисел. Вектор состоит из компонент $d_0$ , $d_1$ и суммы дистанционных компонент его простых составляющих $d_p$ .

$d_0=1'=[1,1,...]$ — вектор из единиц, здесь обозначен как 0-я компонента дистанционных векторов.

$d_1$ — дистанционный вектор единицы. Значения его компонент — это сумма квадратов компонент чисел (не считая 1).

$m(a) = d_1(a) - n(a)$ — скаляр, сферическая степень числа $a$ (не путать с обычной степенью числа). Равна разности суммы квадратов компонент числа $d_1(a)$ и суммы компонент числа $n(a)$ . Если число состоит только из единичных компонент, то его степень равна нулю (лежит на сфере базиса).

$(n(a) - 1)$ — скаляр, барицентрическая координата, соответствующая единичной компоненте в разложении числа.

Значения коэффициентов разложения (6.10) для первых 17 чисел:
\begin{array}{c | c}
a & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 \\
\hline
n (a) & 0 & 1 & 1 & 2 & 1 & 2 & 1 & 3 & 2 & 2 & 1 & 3 & 1 & 2 & 2 & 4 & 1 \\
d_1(a) & 0 & 1 & 1 & 4 & 1 & 2 & 1 & 9 & 4 & 2 & 1 & 5 & 1 & 2 & 2 & 16 & 1 \\
m (a) & 0 & 0 & 0 & 2 & 0 & 0 & 0 & 6 & 2 & 0 & 0 & 2 & 0 & 0 & 0 & 12 & 0 \\
\end{array}
Тождество (6.10) является частным случаем формулы (6.2.1) для пространства чисел.
Приведем явный вид дистанционных векторов для некоторых чисел:

$4:\quad d_4 = (4 - 2) d_0 - (2-1) d_1 + 2d_2 = 2d_0 - d_1 + 2d_2$
$6:\quad d_6 = -d_1 + d_2 + d_3$
$8:\quad d_8 = 6d_0 - 2d_1 + 3d_2$
$30:\quad d_{З0} = -2d_1 + d_2 + d_3 + d_5$
и т.д.

Коэффициенты при векторах $d_i$ — это барицентрические координаты чисел в базисе, образованном простыми числами (за исключением коэффициента при $d_0$ — это степень числа). Можно видеть, что их сумма равна 1.

Псевдоевклидово пространство и скалярная компонента

Присмотревшись к тождеству (6.10), видим, что коэффициент перед дистанционным вектором единицы $d_1$ всегда отрицателен. В то же время коэффициенты при других векторах положительны. То есть реперы на простых числах задают псевдоевклидово пространство. Свойство псевдоевклидовости ему придает наличие единицы, которая играет здесь такую же роль, которую играет время в пространстве-времени Минковского.

Является ли единица числом? Безусловно да. Является ли единица простым числом? Обычный ответ — нет. Почему же тогда единица входит в базисные реперы нашего пространства?
Ответ заключается в том, если единицу исключить, то неожиданно репером становится число 4 (или любое другое составное число). Это означает, что невозможно разложить 4-ку на простые компоненты, если среди компонент нет единицы. Поэтому включение единицы в состав базиса в какой-то степени является вынужденным. Она не похожа на остальные компоненты разложения, но без нее пространство становится «кривым».

Почему дистанционная компонента единицы вычитается из общей суммы дистанций? Ответом является вид матрицы разложения чисел на компоненты $X$ . Единичная компонента любого числа всегда равна 1. Для того, чтобы данный инвариант выполнялся при сложении компонент и требуется компенсирующее вычитание единичной компоненты. Фактически формула (6.8) (приведена в спойлере выше) — это фиксация псевдоевклидовости пространства.

Итак. Свойства времени как компоненты разложения пространства-времени подобны свойствам единицы как компоненты разложения множества целых чисел на произведение простых.

Время — это то, что входит во все пространственные компоненты, неустранимая часть пространства (скорость света — просто единицы измерения данной компоненты). При любом выборе базиса (повороте координат) значение данной составляющей не меняется (единица должна остаться единицей). Поэтому ее приходится компенсировать — вычитать из суммы пространственных дистанций.

Удобно называть данную компоненту скалярной, чтобы отличать ее от остальных — векторных компонент. Обоснованием такого термина может служить тот факт, что при сложении скаляра с вектором его значение прибавляется к каждой компоненте вектора. Единица в пространстве чисел (и время в пространстве-времени) ведут себя схожим образом.

(А почему время «течет»? Возможно, потому что пространство расширяется. Или наоборот. Но тут мы вступаем на зыбкую почву предположений.)

Дистанционный метрический тензор пространства чисел

Интересно рассмотреть структуру псевдоевклидовых пространств. Для этого построим дистанционный (ДМТ) и лапласовский (ЛМТ) метрические тензоры базиса пространства.

ДМТ строится как окаймление вектором единиц $d_0=1'$ матрицы отрицательных полудистанций $D2=-D/2$ между базисными точками пространства. Базисные точки здесь — это простые числа плюс единица.

Дистанции между простыми числами всегда равны 2. Исключение — дистанция между простым числом и единицей, — она равна 1. Начало ДМТ в пространстве чисел выглядит следующим образом:
\begin{array}{c | c c c с c c c}
Dm & * & 1 & 2 & 3 & 5 & 7 & 11 &… \\
\hline
* & & 1 & 1 & 1 & 1 & 1 & 1 &… \\
1 & 1 & &-0.5 &-0.5 & -0.5 &-0.5 &-0.5 &… \\
2 & 1 & -0.5 & & -1 & -1 & -1 & -1 &… \\
3 & 1 & -0.5 &-1 & & -1 & -1 & -1 &… \\
5 & 1 & -0.5 &-1 & -1 & & -1 & -1 &… \\
7 & 1 & -0.5 &-1 & -1 & -1 & & -1 &… \\
11 & 1 & -0.5 &-1 & -1 & -1 & -1 & &… \\
… &… &… &… &… &… &… &… & \\
\end{array}
Видим, что единица — это не совсем простое число.

Лапласовский метрический тензор пространства чисел

Обращая ДМТ, получаем ЛМТ: $Dm \cdot Lm = I$
\begin{array}{c | c c c с c c c}
Lm & * & 1 & 2 & 3 & 5 & 7 & 11 &… \\
\hline
* & l/4 & 1-l/2 & 0.5 & 0.5 & 0.5 & 0.5 & 0.5 &… \\
1 & 1-l/2 & l & -1 &-1 & -1 &-1 & -1 &… \\
2 & 0.5 & -1 & 1 &&&&& \\
3 & 0.5 & -1 && 1 &&&& \\
5 & 0.5 & -1 &&& 1 &&& \\
7 & 0.5 & -1 &&&& 1 && \\
11 & 0.5 & -1 &&&&& 1 & \\
… &… &… &&&&&&… \\
\end{array}
Значения угловой матрицы данного лапласиана зависят от мерности пространства $l=n-1$ , где $n$ — количество вершин в базисе. В углу — значение радиуса описанной сферы базиса $rs=l/4$ .

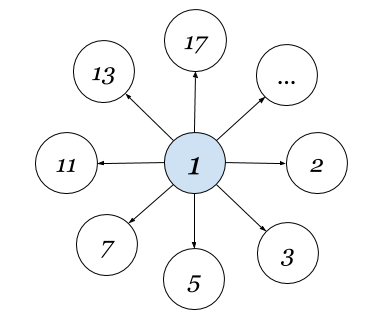
Лапласиан в ЛМТ описывает структуру связности базиса пространства — граф базиса. Видим, что все его вершины связаны только с единицей. Такая топология графа называется звездой. На КДПВ показано, как выглядит такой граф, а значит и базис псевдоевклидового пространства.

Математика — к теории чисел

В определенной нами системе координат чисел базисными реперами являются простые числа. Барицентрическая составляющая в би-координатах чисел совпадает с коэффициентами разложения числа на простые множители. Вот как выглядят би-координаты первых (составных) чисел (колонки таблицы):
\begin{array}{c | c}
Bi & 4 & 6 & 8 & 9 & 10 & 12 & 14 & 15 & 16 & 18 & 20 & 21 & 22 & 24 & 25 \\
\hline
0 & -1 & 0 & -3 & -1 & 0 & -1 & 0 & 0 & -6 & -1 & -1 & 0 & 0 & -3 & -1 \\
1 & -1 & -1 & -2 & -1 & -1 & -2 & -1 & -1 & -3 & -2 & -2 & -1 & -1 & -3 & -1 \\
\hline
2 & 2 & 1 & 3 & & 1 & 2 & 1 & & 4 & 1 & 2 & & 1 & 3 & \\
3 & & 1 & & 2 & & 1 & & 1 & & 2 & & 1 & & 1 & \\
5 & & & & & 1 & & & 1 & & & 1 & & & & 2 \\
7 & & & & & & & 1 & & & & & 1 & & & \\
\end{array}
Нулевая (скалярная) компонента би-координат — это полустепень числа $m2(a) = -m(a)/2$ . Не надо быть специалистом в теории чисел, чтобы понять, что данная функция (сферическая степень числа) должна играть важную роль в описании свойств чисел.

Сферическая степень числа $m(a)$ — это разность квадратов компонент числа и суммы компонент. Например, число 12 раскладывается на такие множители: $12=2^2 \cdot 3^1$ . Тогда его степень будет равна: $m(12)=2^2+1^2-2-1=2$ , а полустепень $-1$ . Исследование свойств функции сферической степени — отдельная тема.

… и к дзета-функция Римана

В заключение перекинем небольшой мостик к огромной и неисчерпаемой дзета-функции Римана.

Сферическая степень числа напоминает известную в теории чисел функцию Мёбиуса только с обратным смыслом. Там, где функция Мёбиуса имеет ненулевое значение, степень числа обращается в нуль. Функция Мёбиуса связана с обратным значением дзета-функции через сумму ряда дробей, в числителе которых значение функции Мёбиуса, а в знаменателе — степень числа.

По аналогии мы рассмотрим аналогичный ряд, только вместо функции Мёбиуса используем простой коэффициент степени. Отметим, что для чисел вида $p^i$ , где p — простое число, сферическая степень не зависит от основания:

$m(p^i)=i^2-i=i(i-1) \quad(6.11)$

Можно использовать (6.11) как определение коэффициента для степени любого числа:

$k(a^i)=k(i)=i(i-1) \quad(6.11')$

Данный коэффициент поместим в числитель дроби, которые просуммируем:

$h = \frac{1}{2} \sum\limits_{a=2} \sum\limits_{i} \frac{k(i)}{a^i} \quad(6.12)$

Из (6.12) вытекает следующее рекурсивное тождество, связывающее значения дзета-функции Римана:

$h = \frac{1}{2} \sum_{i=1}^\infty k(i)(\zeta(i)-1) = \zeta(2) + \zeta(3) \quad(6.13)$

Здесь $\zeta(i)$ — значение дзета-функции Римана для положительных целых чисел.
$\zeta(2) = \pi^2/6$ — сумма обратных квадратов,
$\zeta(3) = 1.202...$ — константа Апери, сумма обратных кубов.

Подробности вывода тождества (6.12) для интересующихся

$\sum\limits_{i} \frac{k(i)}{a^i} = \frac{2a}{(a-1)^3}$

$h = \sum\limits_{a=2} \frac{a}{(a-1)^3} = (b=a-1)= \sum\limits_{b=1} (\frac{1}{b^2}+\frac{1}{b^3}) = \zeta(2) + \zeta(3)$

С другой стороны, меняя порядок суммирования, получаем:

$h = \frac{1}{2} \sum\limits_{i} k(i) \sum\limits_{a=2} \frac{1}{a^i}$ , но
$\sum\limits_{a=2} \frac{1}{a^i}=\zeta(i)-1$

Собирая все вместе, получаем (6.13).

Наверное данное тождество можно как-то вывести из известных и опубликованных, но быстро нам это сделать не удалось (возможно, кто-то из продвинутых читателей подскажет, куда тут надо ткнуться). В любом случае формула (6.13) является хорошим завершающим аккордом всей серии.

Мы рассказали все, что планировали в рамках данной серии (и даже больше). Поставленная цель — дать основные понятия и соотношения, связанные с системами координат на точечном базисе, — достигнута. В статьях сделана попытка соединить понятия, принадлежащие казалось бы разным областям. (И кажется, что многое можно свести к понятию скалярного произведения разных объектов). Такое соединение всегда полезно, потому что уменьшает количество сущностей и позволяет проводить аналогии. (Например, между понятиями единицы и времени).

Правильные понятия и осмысленные формулы (или наоборот) не стареют — это фундамент для решения как теоретических, так и прикладных задач.
Спасибо всем за поддержку!