Где и как врубиться в эмбеддинги графов
Привет, Хабр!
Три года назад на сайте Леонида Жукова я ткнул ссылку на курс Юре Лесковека cs224w Analysis of Networks и теперь мы будем его проходить вместе со всеми желающими в нашем уютном чате в канале #class_cs224w. Cразу же после разминки с открытым курсом машинного обучения, который начнётся через несколько дней.

Вопрос: Что там начитывают?
Ответ: Современную математику. Покажем на примере улучшения процесса IT-рекрутинга.
Под катом читателя ждёт история о том, как руководителя проектов дискретная математика до нейросетей довела, почему внедряющим ERP и управляющим продуктами стоит почитывать журнал Биоинформатика, как появилась и решается задача рекомендации связей, кому нужны графовые эмбеддинги и откуда взялись, а также мнение о том, как перестать бояться вопросов про деревья на собеседованиях, и чего всё это может стоить. Погнали!
План у нас такой:
1) Что такое cs224w
2) Шашечки или ехать
3) Как я до всего этого докатился
4) Зачем почитывать журнал Биоинформатика
5) Что такое графовые эмбеддинги и откуда взялись
6) Случайный бродяга в форме матрицы
7) Возвращение случайного бродяги и сила связей
8) Путь случайного бродяги и вершина в векторе
9) Наши дни — случайный бродяга для всех и каждого
10) Как и где такие данные хранить и откуда брать
11) Чего опасаться
12) Памятка воспроизводителю
Курс Юре Лесковека Analysis of Networks выделяется в плеяде образовательных продуктов факультета вычислительных наук университета Стенфорда. Отличие от прочих в том, что программа охватывает очень широкий спектр вопросов. Именно междисциплинарный характер делает приключение вызовом. Призом же становится универсальный язык описания сложных систем — теория графов, разобраться с которой предлагается за десять недель.

Курс не стоит себе так, а открывает программу Mining Massive Data Sets Graduate Certificate, в которой ещё много вкусного.
Вторым в приключении идёт CS229 Machine Learning Эндрю Ына, который рекламировать излишне.
Далее следует CS246 Mining Massive Data Sets Юре Лесковека, в котором желающим предлагается упороться MapReduce и Spark-ом.
Завершает банкет CS276 Information Retrieval and Web Search Криса Маннинга.
В качестве бонуса предлагается CS246H Mining Massive Data Sets: Hadoop Labs специально для тех, кому было мало. Опять в гостях у Юре.
В целом, обещают, что прошедшие программу приобретут навыки и знания, достаточные для поиска информации в интернете (без всяких гуглов и иже им подобных).
Когда-то давно мой руководитель и ментор, на тот момент — СТО в украинском Nestlé, втолковывал мне, молодому и амбициозному, порывавшемуся получить МВА чтобы стать ещё звездатее, истину о том, что на рынке труда покупают и продают опыт и знания, а не дипломы и результаты тестов.
Описанную выше специализацию можно пройти онлайн за символические $18,900.
В среднем, приключение занимает 1–2 года, но не более 3. Для получения сертификата требуется пройти все курсы с оценкой не ниже В (3.0).
Есть и другой путь.
Все материалы курсов Юре Лесковека публикуются открыто и весьма оперативно. Поэтому желающие могут страдать в любое удобное время, согласуя нагрузку со способностями. Особо одарённым рекомендую попробовать режим приключения «Это Стенфорд, лапочки!» — прохождение параллельно курсу — видеозаписи лекций выкладывают в течении пары дней, дополнительная литература доступна сразу, домашки и решения открываются постепенно.
В этот сезон, после окончания Открытого Курса Машинного Обучения на Хабре, который полезно пройти в качестве разминки, мы устроим забег в выделенном канале #class_cs224w чата ods.ai.
Рекомендуется обладать следующим набором навыков:
- Основы вычислительных наук на уровне, достаточном для написания нетривиальных программ.
- Основы теории вероятностей.
- Основы линейной алгебры.
Жил себе, не тужил. Руководил проектами внедрения SAP. Временами — выступал в роли играющего тренера по своей основной специализации — и гайки CRM крутил. Можно сказать, почти никого не трогал. Самообразованием занимался. В какой-то момент решил специализироваться в области трансформации бизнеса (или проведении организационных изменений). Задача анализа организаций до и после перемен — важная часть этой работы. Знание откуда и куда меняться — здорово помогает. Понимание связей между людьми — весомый фактор успеха. Несколько лет уделил изучению «мягких» методологий исследования организаций, да всё никак удовлетвориться не мог — вопросом: «А кто кого заборет: главнокоммивояжер главносчетовода, или же завскладом всех сильнее?» задаюсь уж несколько лет кряду. Всё ищу способ наверняка измерить.
Переломным стал 2014 год, когда я отказался от грёз о МВА и в качестве второго высшего выбрал (тут звучит барабанная дробь) снова статистику и управление информацией в новом лиссабонском университете (первое — и ныне здравствующая кафедра телекоммуникаций уже несуществующего факультета авиационных и космических систем киевского политеха + кафедра связи на военке).
В первый же семестр второй магистратуры распробовал анализ социальных сетей — одно из применений теории графов. Тогда-то и узнал, что вот-то оно что, оказывается, есть алгоритмы, которые решают задачи вроде кто с кем против команды внедрения новых технологий дружить будет, а я-то раньше не знал и голову сушил, анализируя связи людей в уме — она от этого реально пухнет. Совершенно случайно оказалось, что анализ сетей, после первых шагов, — это сплошное копание данных и машинное обучение то с учителем, то без.
Поначалу хватало классики.
Захотелось большего. Чтобы разобраться с эмбеддингами (и перепилить под свои задачи работы Маринки Житник), пришлось вникать в глубокое обучение, в чём здорово помог курс о Deep Learning на пальцах. Учитывая то, с какой скоростью группа Лесковека создаёт новое знание, для того, чтобы решать управленческие задачи автоматически, достаточно просто следить за их работой.
Командообразование — задача непростая. Кого с кем в одну лодку садить не стоит — один из насущных вопросов. Особенно, когда лица новые. И местность незнакомая. А вести к далёким берегам нужно не одну лодку, но целую флотилию. И в пути обязательно тесное взаимодействие как в лодках, так и между ними. Обычные будни внедрения SAP, когда Заказчику нужно поставить сконфигурированную под его специфику систему из кучи модулей, и план проекта состоит из тысячи строк. За всю свою рабочую деятельность, ни разу никого не нанимал — всегда выдавали команду. Ты — руководитель проектов, на тебе полномочия, и крутись. Как-то так. Выкручивался.
Пример из жизни:Я-то сам не собеседовал, но тимлидов для этого выделял. А за ресурсы — спрос с меня. И интеграция новых членов команды — тоже область ответственности руководителя проекта. Полагаю, многие согласятся с тем, что чем качественнее подготовлен список кандидатов, тем процесс приятнее для всех участников. Эту задачу мы и рассмотрим в деталях.
Природная лень требовала — найди способ автоматизации. Нашёл. Делюсь.
Немного управленческой теории. Методология Адизеса основана на базовом принципе: организации, как живые организмы, имеют свой жизненный цикл и демонстрируют предсказуемые и повторяющиеся поведенческие проявления в процессе роста и старения. На каждом этапе организационного развития компанию ожидает специфичный набор проблем. То, насколько хорошо менеджмент компании справляется с ними, насколько успешно осуществляет изменения, необходимые для здорового перехода с этапа на этап, и определяет конечный успех или неудачи этой организации.
С идеями Ицхака Адизеса я знаком уже лет десять и во многом согласен.
Личности сотрудников — как витамины — влияют на успех в определенных условиях. Известны примеры того, как успешные руководители, перейдя из одной отрасли, проваливались в другой. Бывает и хуже. Например, Марисса Майер, поднявшая поиск Google, уронила Yahoo. Уоррен Баффет говорит, что навряд-ли добился бы успеха, родившись в Бангладеш. Среда и способы взаимодействия в ней — важный фактор.
Хорошо бы предсказывать осложнения до экспериментов на живом, верно?
В эту канву ложится очередное исследование Маринки Житник, опубликованное в журнале Биоинформатика. Задача предсказания побочных эффектов при совместном применении препаратов математически близка к управленческой. Всё благодаря универсальности языка графов. Рассмотрим её детальнее.

Графовая свёрточная сеть Decagon — инструмент предсказания связей в мультимодальных сетях.
Метод состоит в построении мультимодального графа взаимодействий белок-белок, препарат-белок, и побочных эффектов от комбинации препаратов, которые представляются связями препарат-препарат, где каждый из побочных эффектов — ребро определённого типа. Decagon предсказывает конкретный вид побочного эффекта, если таковой есть, который проявляется в клинической картине.
На рисунке приведен пример графа побочных эффектов, полученных из данных генома и популяции. Всего — 964 различных вида побочных эффектов (обозначенных рёбрами типа ri, i = 1, …, 964). Дополнительная информация в модели представлена в виде векторов свойств протеинов и препаратов.
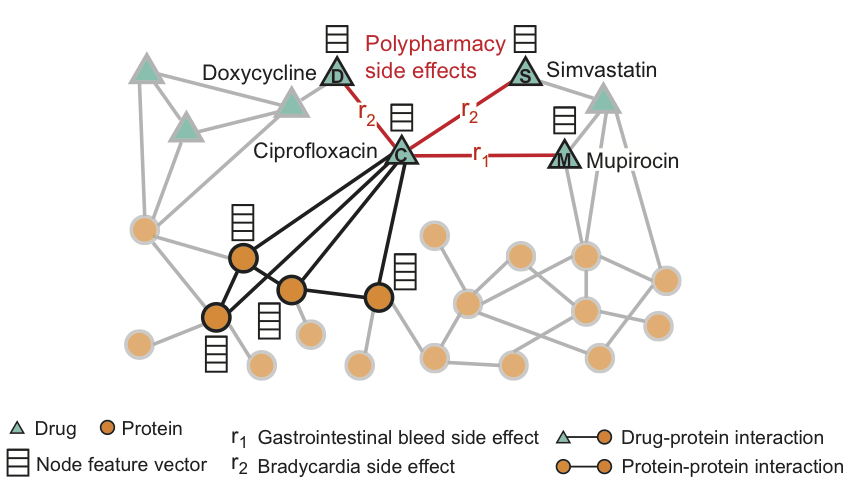
Для препарата Ciprofloxacin (узел C) подсвеченные соседи по графу отражают воздействия на четыре белка и три других препарата. Мы видим, что Ciprofloxacin (узел C), принятый одновременно с Doxycycline (узел D) или Simvastatin (узел S), повышают риск побочного эффекта, выражающегося в замедлении сердечного ритма (побочный эффект типа r2), а комбинация с Mupirocin (M) — повышает риск кровотечений желудочно-кишечного тракта (побочный эффект типа r1).
Decagon предсказывает ассоциации между парами препаратов и побочными эффектами (показаны красным) с целью идентификации побочных эффектов от одновременного приёма, т.е. тех побочных эффектов, которые нельзя связать ни с одним из препаратов из пары по-отдельности.
Архитектура графовой свёрточной нейронной сети Decagon:
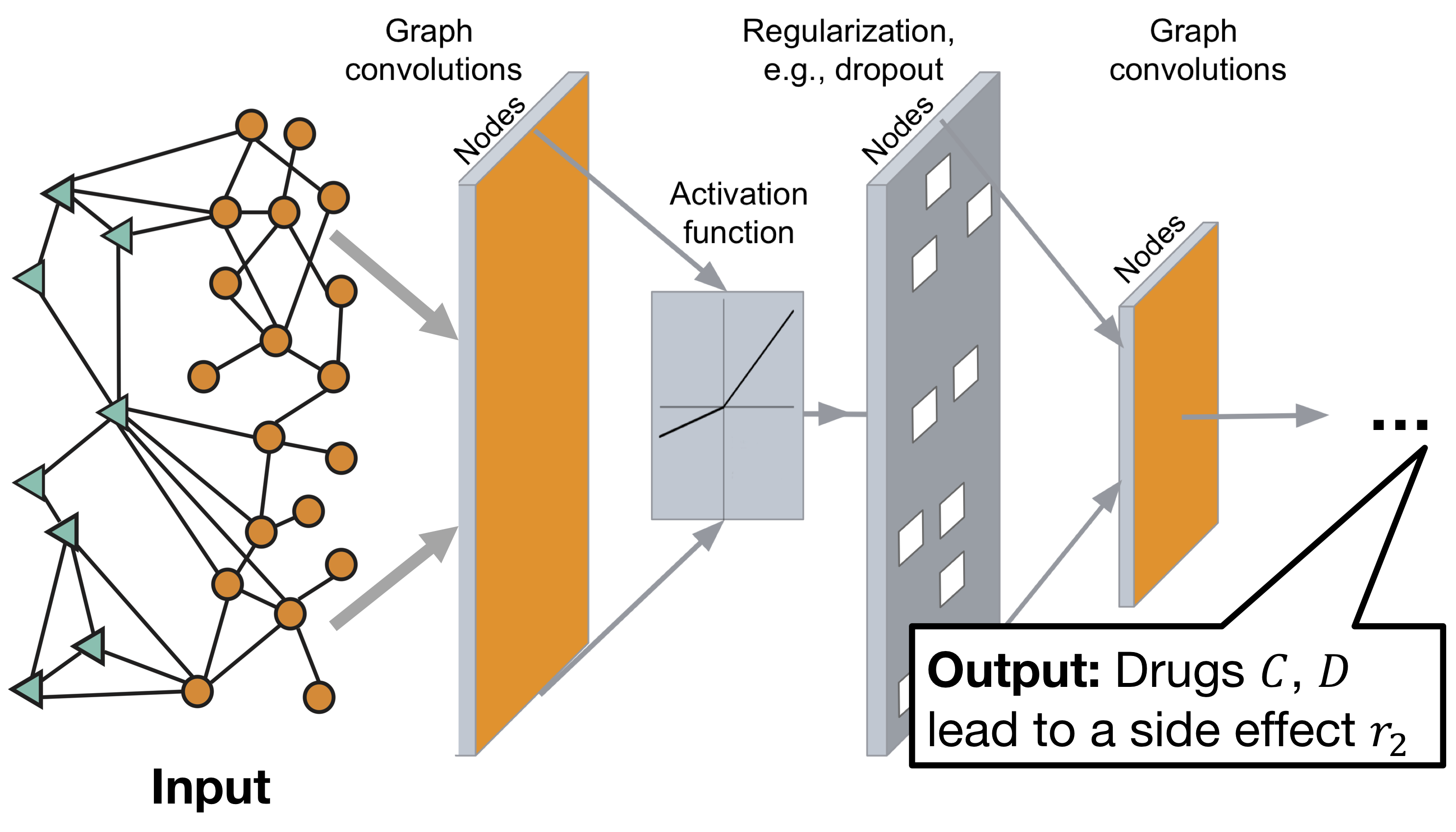
Модель состоит из двух частей:
Энкодер: графовая свёрточная сеть (GCN) принимающая граф и производящая эмбеддинги для узлов,
Декодер: тензорная факторизационная модель, использующая эти эмбеддинги для выявления побочных эффектов.
Подробнее можно узнать на сайте проекта или ниже по тексту.
Здорово, а как это к командообразованию прикрутить?
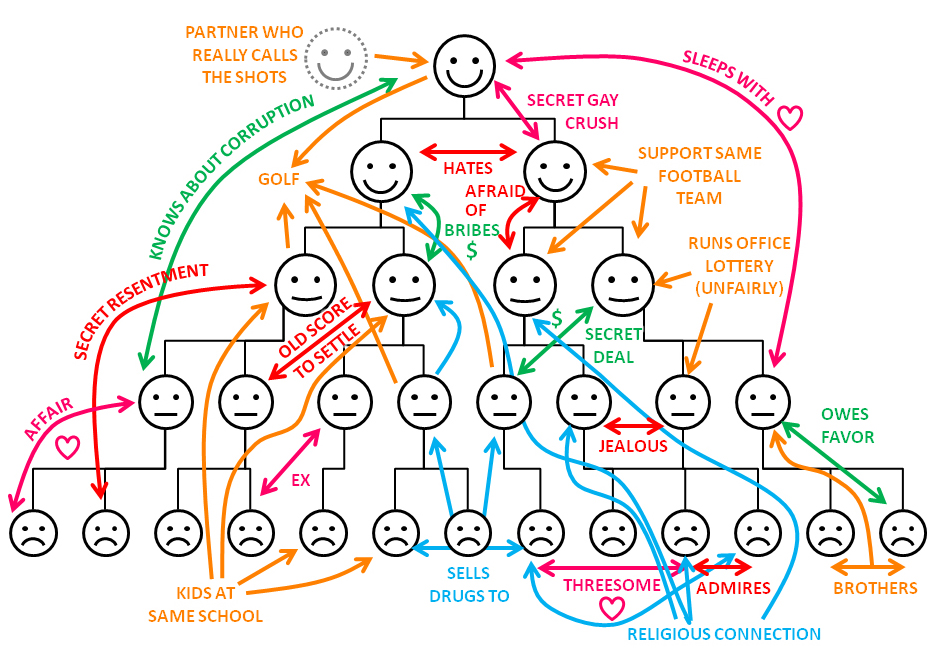
Как-то так.
Вот для того, чтобы чувствовать себя комфортно в области исследований, подобных описанному, и стоит копнуть гранит науки. Правда, копать доведётся интенсивно — теория графов активно развивается. На то оно и остриё прогресса — там мало кому комфортно бывает.
Чтобы разобраться с деталями функционирования Decagon, совершим экскурс в историю.
Мне случилось наблюдать изменение в наборе передовых методов решения задач предсказания связей на графах на протяжении минувших четырёх лет. Это было забавно. Почти как в сказке — чем дальше, тем страшнее. Эволюция прошла по пути от эвристик, определявших окружение для вершины графа, к случайным бродягам, потом появились спектральные методы (анализ матриц), и вот теперь — нейронные сети.
Сформулируем задачу предсказания связей:Рассмотрим ненаправленный граф $inline$\begin{align*}G (V, E)\end{align*}$inline$, где
$inline$\begin{align*}V\end{align*}$inline$ — множество вершин $inline$\begin{align*}v\end{align*}$inline$,
$inline$\begin{align*}E\end{align*}$inline$ — множество рёбер $inline$\begin{align*}e (u, v)\end{align*}$inline$, соединяющих вершины $inline$\begin{align*}u\end{align*}$inline$ и $inline$\begin{align*}v\end{align*}$inline$.Определим множество всех возможных рёбер $inline$E^{\diamond}$inline$, его мощность
$inline$\begin{align*} |E^{\diamond}| &= \frac{|V|*(|V| — 1)}{2}\\ \end{align*}$inline$, где
$inline$\begin{align*}|V| = n\end{align*}$inline$, — количество вершин.Очевидно, что множество несуществующих рёбер можно выразить как $inline$\begin{align*}\overline{E} = E^{\diamond} — E\end{align*}$inline$.
Мы предполагаем, что в множестве $inline$\begin{align*}\overline{E}\end{align*}$inline$ есть пропущенные связи, либо связи, которые появятся в будущем, и хотим их найти.
Решение сводится к определению функции $inline$\begin{align*}D (u, v)\end{align*}$inline$ дистанции между вершинами графа, позволяющей по структуре графа $inline$\begin{align*}G (t_0, t_0^\star)\end{align*}$inline$, заданной на промежутке времени $inline$\begin{align*}(t_0, t_0^\star)\end{align*}$inline$, предсказать появление рёбер $inline$\begin{align*}G (t_1, t_1^\star)\end{align*}$inline$ в интервале $inline$\begin{align*}(t_1, t_1^\star)\end{align*}$inline$.
Одна из первых публикаций, которая предлагает перейти от кластеризации к задаче предсказания связей в контексте изучения совместной экспрессии генов, появилась в журнале (как нетрудно догадаться) Биоинформатика в 2000 году. Уже в 2003 вышла статья Джона Клейнберга с обзором актуальных методов решения задачи прогнозирования связей в социальной сети. Его книга «Networks, Crowds, and Markets: Reasoning About a Highly Connected World» — учебник, который рекомендуется читать во время прохождения курса cs224w, большинство глав — указаны в разделе обязательной к прочтению литературы.
Статью можно считать срезом знания в узкой области, как мы видим, поначалу ассортимент методов был невелик и включал в себя:
- Методы, основанные на соседях по графу — и самым очевидным из них является количество общих соседей.
Дадим определение:Вершина $inline$u$inline$ является соседом по графу для вершины $inline$v$inline$, если ребро $inline$e (u, v) \in E$inline$.
Обозначим $inline$\Gamma (u)$inline$ множество соседей вершины $inline$u$inline$,
тогда дистанция между вершинами $inline$u$inline$ и $inline$v$inline$ может быть записана как
$inline$D_{CN}(u, v) =\Gamma (u) \cap \Gamma (v)$inline$.
Интуитивно понятно, что чем больше пересечение множеств соседей двух вершин, тем более вероятна связь между ними — так, например, большинство новых знакомств происходят с друзьями друзей.
Более продвинутые эвристики — коэффициент Жаккара $inline$D_J (u, v) =\frac{\Gamma (u) \cap \Gamma (v)}{\Gamma (u) \cup \Gamma (v)}$inline$ (которому уже тогда было сто лет) и недавно (на то время) предложенная дистанция Адамик/Адар $inline$D_{AA}(u, v) =\sum_{x \in \Gamma (u) \cap \Gamma (v)}\frac{1}{\log|\Gamma (x)|}$inline$ развивают идею путем нехитрых преобразований.
- Методы, базирующиеся на путях по графу — идея в том, что кратчайший путь между двумя вершинами на графе соотносится с шансом появления связи между ними — чем путь короче, тем шанс выше. Можно пойти дальше и учитывать не только кратчайший, но и все прочие возможные пути между парами вершин, например, взвешивать пути, как это делает дистанция Катца. Уже тогда упоминается ожидаемая длина пути случайного бродяги — предтеча основы метода рекомендации знакомых в Фейсбук.
Оценим качество прогноза:
- Для каждой пары вершин $inline$(u, v)$inline$ каждого несуществующего ребра $inline$e (u, v)\in\overline{E}$inline$ вычислим дистанцию $inline$D (u, v)$inline$ на графе $inline$G (t_0, t_0^\star)$inline$.
- Отсортируем пары $inline$(u, v)$inline$ по убыванию дистанции $inline$D (u, v)$inline$.
- Отберём $inline$m$inline$ пар с наибольшими значениями — это наш прогноз.
- Посмотрим, сколько из предсказанных рёбер появились в $inline$G (t_1, t_1^\star)$inline$.
Важно помнить, что количество общих соседей и дистанция Адамик/Адар — мощные методы, задающие базовый уровень качества прогноза по одной только структуре связей, и если ваша система рекомендаций показывает результат слабее, то что-то не так.
Обобщённо, графовые эмбеддинги — это способ представления графов компактно для задач машинного обучения с помощью функции преобразования $inline$\begin{align*}\phi: G (V, E)\longmapsto\mathbb{R}^d\end{align*}$inline$.
Мы рассмотрели несколько таких функций, самые эффективные из первых. Более широкий перечень описан в статье Клейнберга. Как мы видим из обзора, уже тогда начинали применять высокоуровневые методы, вроде разложения матриц, предварительной кластеризации, и инструменты из арсенала вычислительной лингвистики. Пятнадцать лет назад всё только начиналось. Эмбеддинги были одномерные.
Следующей вехой на пути к тем самым графовым эмбеддингам стало развитие методов случайных блужданий. Придумывать и обосновывать новые формулы для вычисления дистанции, видимо, стало влом. В некоторых приложениях, похоже, стоит просто полагаться на волю случая и довериться бродягам.
Дадим определение:Матрица смежности графа $inline$G$inline$ с конечным числом вершин $inline$n$inline$ (пронумерованных числами от 1 до $inline$n$inline$) — это квадратная матрица $inline$A$inline$ размера $inline$n \times n$inline$, в которой значение элемента $inline$a_{ij}$inline$ равно весу $inline$w_{ij}$inline$ ребра $inline$e (i, j)$inline$.
Примечание: здесь мы намеренно отойдём от использовавшихся ранее индикаторов вершин $inline$u, v$inline$ и будем использовать привычные для линейной алгебры и вообще в работе с матрицами обозначения $inline$i, j$inline$.
Проиллюстрируем рассмотренные концепции:
Пусть $inline$G$inline$ — граф из четырёх вершин $inline$\{A, B, C, D\}$inline$, соединенных рёбрами.
С целью упрощения построений, примем допущение, что рёбра нашего графа — двунаправленные, т.е. $inline$\forall e (i, j) \in E, \exists e (j, i) \in E \land w_{ij} = w_{ji}$inline$.
$inline$e (A, B), w_{AB} = 1;\\ e (B, C), w_{BC} = 2;\\ e (A, C), w_{AC} = 3;\\ e (B, C), w_{BC} = 1. $inline$
Изобразим множества рёбер: $inline$E$inline$ — синим, а $inline$\overline{E}$inline$ — зелёным цветом.
$inline$\begin{align*}A = \left[ \begin{matrix} 0 & 1 & 3 & 0\\ 1 &0 & 2 & 1\\ 3 & 2 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix} \right]\end{align*}$inline$
Запись графа в матричной форме открывает интересные возможности. Чтобы их продемонстрировать, заглянем в работу Сергея Брина и Ларри Пейджа, и разберёмся с тем, как работает PageRank — алгоритм ранжирования вершин графа, до сих пор являющийся важной частью поиска Google.
PageRank — придуман, чтобы искать самые лучшие страницы в интернете. Страница считается хорошей, если её ценят (ссылаются на неё) другие хорошие страницы. Чем больше страниц содержат ссылки на неё, и чем выше их рейтинг, тем выше PageRank для данной страницы.
Рассмотрим интерпретацию работы метода с помощью цепей Маркова.
Дадим определение:Степень вершины (degree) — мощность множества соседей:
$inline$d_i = |\Gamma (i)|$inline$,Различают in-degree и out-degree. Для нашего примера они эквивалентны.
Построим взвешенную матрицу смежности, руководствуясь правилом:
$inline$\begin{align*}M_{ij} = \left\{ \begin{matrix} \frac{1}{d_j} & \forall i, j \iff i \in \Gamma (j), \\ 0 & \forall i, j \iff i \notin \Gamma (j). \end{matrix} \right.\end{align*}$inline$$inline$\begin{align*}M = \left[ \begin{matrix} 0 & \frac{1}{3} & \frac{1}{2} & 0 \\ \frac{1}{2} &0 & \frac{1}{2} & 1 \\ \frac{1}{2} & \frac{1}{3} & 0 & 0\\ 0 & \frac{1}{3} & 0& 0 \end{matrix} \right]\end{align*}$inline$
Обратите внимание, что столбцы $inline$M$inline$ должны в сумме давать 1 (т.е. $inline$M$inline$ — «столбцовая стохастическая матрица»). Элементы каждого столбца задают вероятность перехода из вершины $inline$j$inline$ в одну из соседних вершин по графу $inline$i \in \Gamma (j)$inline$ .
Пусть $inline$r_i$inline$ будет значением PageRank для вершины $inline$i$inline$, у которой $inline$d_i$inline$ исходящих рёбер. Тогда мы можем выразить PageRank для её соседа $inline$j$inline$ как
$$display$$r_j = \sum_{i \to j}\frac{r_i}{d_i}$$display$$
Таким образом, каждый из соседей $inline$i$inline$ вершины $inline$j$inline$ вносит вклад в её PageRank, и его размер прямо пропорционален авторитету соседа (т.е. его PageRank), и обратно пропорционален размеру окружения соседа.
Мы можем и будем хранить значения PageRank для всех вершин в векторе $inline$\begin{align*}r = [r_1, r_2, …, r_n]^T \end{align*}$inline$ — это позволит записать уравнение компактно в виде скалярного произведения:
$$display$$r = Mr$$display$$
Представьте веб-сёрфера, который проводит бесконечное количество времени в интернете (что недалеко от реальности). В любой момент времени $inline$t$inline$ он находится на странице $inline$i$inline$ и в момент $inline$t+1$inline$ переходит по одной из ссылок на одну из соседних страниц $inline$j \in \Gamma (i)$inline$, выбирая её случайным образом, причём все переходы — равновероятны.
Обозначим $inline$p (t)$inline$ вектор с вероятностями того, что сёрфер находится на странице $inline$i$inline$ в момент времени $inline$t$inline$. $inline$p (t)$inline$ — распределение вероятностей между страницами, поэтому сумма элементов равна 1.
Вспомним, что $inline$M_{ij}$inline$ — это вероятность перехода от вершины $inline$j$inline$ к вершине $inline$i$inline$ с учётом того, что сёрфер находится на вершине $inline$j$inline$ и $inline$p_j (t)$inline$ — вероятность того, что он находится на странице $inline$j$inline$ в момент $inline$t$inline$. Поэтому, для каждой вершины $inline$i$inline$
$$display$$p_i (t+1) = M_{i1}p_1(t) + M_{i2}p_2 + . . . + M_{in}p_n (t)$$display$$
и это значит, что
$$display$$p (t + 1) = Mp (t)$$display$$
Если случайные блуждания когда-либо достигнут состояния, в котором $inline$p (t + 1) = p (t)$inline$, тогда $inline$p (t)$inline$ — стационарное распределение. Вспомним, что уравнение для PageRank в векторной форме $inline$r = Mr$inline$. Вывод — вектор $inline$r$inline$ значений PageRank — это стационарное распределение случайного бродяги!
На практике для $inline$r$inline$ уравнение PageRank зачастую решается степенным методом. Идея в том, что мы инициализируем вектор $inline$r^{(t0)} = [1/n, 1/n, …, 1/n]^T $inline$ одинаковыми значениями и последовательно вычисляем $inline$r^{(t+1)} = Mr^{(t)}$inline$ для каждого $inline$t$inline$ до тех пор, пока значения не сойдутся, т.е. $inline$||r^{(t+1)} — r^{(t)}||_1 < \epsilon$inline$, где $inline$\epsilon$inline$ — допустимая погрешность. (Обратите внимание, что $inline$||x||_1 = \sum_{k} |x_k|$inline$ — это $inline$L_1$inline$ норма, или дистанция Минковского). Тогда значения вектора $inline$r^{(t+1)}$inline$ и будут оценкой Page Rank для вершин. Как правило, хватает 20-30 итераций.
Здесь мемасик про решение задач случайным перебором приобретает новые оттенки.

В описанном «ванильном» виде метод чувствителен к двум проблемам:
- Т.н. «паучьи гнёзда» — вершины, ссылающиеся на себя — приводит к тому, что PageRank в них втекает. Весь. И никому больше не достаётся.
- Тупики — вершины с одними только входящими рёбрами — через них PageRank утекает из системы. И заканчивается в какой-то момент. Вектор $inline$r$inline$ заполняется нулями.
Брин с Пейджем решили проблему 20 лет назад, выдав бродяге дробовик телепорт!
Пусть наш веб-сёрфер с вероятностью $inline$\beta $inline$ выбирает исходящую ссылку, а с вероятностью $inline$1 — \beta $inline$ — телепортируется на случайно выбранную страницу. Обыкновенно значение $inline$1 — \beta \approx 0.15 $inline$, т.е. наш веб-сёрфер делает 5–7 шагов между телепортациями. Из тупика — всегда телепортируется. Уравнение для PageRank принимает вид:
$$display$$r_j = \sum_{i \to j}\beta\frac{r_i}{d_i} + (1-\beta)\frac{1}{n}$$display$$
(данная формулировка предполагает, что в графе нет тупиков)
Подобно нашей предыдущей матрице $inline$M $inline$, мы можем определить новую матрицу
$$display$$ M^{\star} = \beta M + (1-\beta) [1/n]_{n×n} $$display$$
вероятности переходов. Остаётся решить уравнение $inline$ r = M^{\star}r $inline$ аналогичным способом. Ради сохранения интриги, просто скажу, что обобщённый алгоритм описан на слайдах 37–38 в 14-й лекции курса cs224w 2017 года, в которой Юре прекрасно раскрывает все детали и показывает, как метод используется у них в Pinterest (он там главный по науке).
Вернёмся к делам менеджерским. Какой практический толк от всех этих матричных операций?
Обозначим несколько задач руководителя проекта:
- Выделить ключевых стейкхолдеров;
- Определить связи между участниками проекта;
- Подобрать участников групп, наиболее подходящих коллективам.
Первая задача решается построением графа связей и применением классического PageRank. Так, например, мы выловили г-на Барака Обаму из переписки, которой любезно поделилась г-жа Хиллари Клинтон в то время как прочие методы не уделили ему должного внимания.
Оставшиеся две — потребуют модификации алгоритма.
В реальном мире это заняло восемь лет.
Напомним, что ранее наш бродяга с телепортом перемещался в случайно выбранную вершину. А что если мы ограничим множество возможных перемещений неслучайной выборкой по какому-нибудь критерию? Так и сделали в 2006 году коллеги Юре по аспирантуре.
Усовершенствуем наш пример:Допустим, мы что-то знаем о вершинах рассматриваемого графа $inline$G $inline$, какие-то признаки.
Для каждой вершины $inline$i $inline$ зададим вектор из $inline$k $inline$ свойств $inline$f^{(i)} = [f_1, f_2, …, f_k]^T $inline$.
Пусть первое из них, $inline$f_1 $inline$ будет, скажем, любимый цвет глаз.
Предположим, что читатель дослужился до высоких рангов и у него уже есть команда, которая трудится над созданием нового революционного продукта. В какой-то момент возникает потребность добавить ещё одного игрока. Допустим, что пул кандидатов — достаточно обширный (например, у нас дядя работает на фабрике датасаентистов). Для того, чтобы облегчить жизнь нашему IT-рекрутеру в формировании списка тех, кого мы пригласим собеседоваться с ключевыми участниками команды (их время тоже дорого стоит) — будем решать её алгоритмически.
Допустим, вопрос, которым мы задались — подготовить ранжированный по критерию потенциальной совместимости список кандидатов, наиболее подходящих двум нашим игрокам, $inline$A $inline$ и $inline$C $inline$ — им голубоглазые симпатичны.
Мы знаем, что предыдущее успешное сотрудничество — залог успеха сотрудничества будущего.
Поэтому построим граф связей датасаентистов из истории командных выступлений в соревнованиях на какой-нибудь площадке, вроде Kaggle или Hackerrank, которая позволяет участникам не только мериться математикой, но и общаться на форумах, ставить лайки кернелам и всё такое (предположим, что читатель уже сделал это).
Дадим определение:Персонализированной выборкой $inline$S_k (x) $inline$ по значению $inline$x $inline$ критерия $inline$ k $inline$, назовём подмножество вершин графа $inline$G$inline$:
$inline$\forall i \in V, i \in S_k (x) \iff f^{(i)}_{k} = x$inline$
Остаётся построить персонализированную матрицу вероятности переходов:
$inline$\begin{align*}M^{p}_{ij} = \left\{ \begin{matrix} \beta M_{ij} + \frac{1-\beta}{|S_k (x)|} & \forall i, j \iff i \in S_k (x), \\ \beta M_{ij} & \forall i, j \iff i \notin S_k (x). \end{matrix} \right.\end{align*}$inline$
И решить уравнение $inline$\begin{align*} r = M^{p} r \end{align*}$inline$ относительно $inline$\begin{align*} r \end{align*}$inline$, как мы это уже не раз делали. В векторе $inline$\begin{align*} r \end{align*}$inline$ содержатся значения персонализированного PageRank по отношению к нашей выборке — наиболее относящиеся к ней вершины. Для решения вопроса с поиском потенциальных кандидатов, отсортируем содержимое $inline$\begin{align*} r \end{align*}$inline$ по убыванию значений — нас интересует вершина списка.
Именно этот метод отвечает за подготовку 80% рекомендаций в Pinterest.
Частный случай, когда $inline$\begin{align*}|S_k (x)| = 1\end{align*}$inline$, называется Random Walks with Restarts — бродяги возвращаются и возвращаются в одну интересующую нас вершину. В результате мы получаем меру близости для каждой вершины графа по отношению к той единственной. И это решает задачу предсказания связей лучше, чем позволяет дистанция Адамик/Адар.
Добавим ещё улучшений:Вспомним, что рёбра $inline$\begin{align*} e (i, j) \in E \in G \end{align*}$inline$ нашего графа имеют веса $inline$\begin{align*}w_{ji}\end{align*}$inline$.
Это позволит задать взвешенную матрицу $inline$\begin{align*}M^w\end{align*}$inline$ вероятности переходов:
$inline$\begin{align*}M^{w}_{ij} = \left\{ \begin{matrix} \frac{w_{ij}}{\sum_{j}w_{ij}} & \forall i, j \iff e (i, j) \in E, \\ 0 & \forall i, j \iff e (i, j) \notin E. \end{matrix} \right.\end{align*}$inline$
Бродяга будет совершать переходы по-прежнему случайно, но уже не равновероятно!
Внимательный читатель уже задался вопросом о том, как же эти веса померять.
Этим же озадачились в Facebook в 2011. Нужно было построить систему рекомендации друзей из друзей друзей, да так, чтобы максимизировать создание новых связей. И первым шагом было создание взвешенного графа связей между пользователями из информации в их профилях и истории взаимодействия (лайки, сообщения, совместные фото и прочее). Как-то силу дружбы в интернете померять.
$$display$$ w_{ij} = f^w (i, j) = e^{- \sum_{z}{\xi_z x_{ij}[z]}} ,$$display$$
где $inline$\begin{align*}x_{ij} \end{align*}$inline$ — вектор свойств вершин и соединяющего их ребра, т.е. $inline$\begin{align*}x_{ij} = f^{(i)} \cup f^{(j)} \cup f^{e (ij)} \end{align*}$inline$, а $inline$\begin{align*}\xi \end{align*}$inline$ — вектор весов, которые предстоит выучить из данных.
Здесь подготовленный читатель узнает линейную модель, а неподготовленный — задумается о том, что стоит пройти открытый курс машинного обучения, чтобы разобраться с градиентным спуском, с помощью которого мы и выучим значения весов в векторе $inline$x_{ij} $inline$ — они покажут, как влияют лайки и сообщения на дружбу в интернете.
Зачем нам это всё надо?
Кроме того, что рассматриваемый подход позволяет предсказывать связи ещё лучше, мы можем выучить правила успешного командообразования. И узнать, на что обращать внимание в будущем.
Напомним условия нашего упражнения. Мы наблюдаем за развитием сотрудничества (совместное участие в соревнованиях) в группе условных датасаентистов на интервале $inline$\begin{align*}(t_0, t_0^\star)\end{align*}$inline$ (например, один календарный месяц) и хотим предсказать командообразование в интервале $inline$\begin{align*}(t_1, t_1^\star)\end{align*}$inline$ (другой месяц). Кроме участия в соревнованиях, мы отслеживаем общение на форумах, лайки кернелов, и ещё чего заблагорассудится. Всю собранную информацию храним в матрице $inline$X^{\star} \in \mathbb{R}^{(2k+l)\times|E|} $inline$ (её колонки — вектора $inline$x_{ij} $inline$, $inline$k, l$inline$ — размерности векторов свойств вершин и рёбер $inline$f^{(i)}, f^{e (ij)}$inline$, соответственно) и графе $inline$\begin{align*}G \end{align*}$inline$ для двух интервалов времени.
Подготовим данные для машинного обучения.
Для каждой вершины $inline$\begin{align*} i\end{align*}$inline$:
1) определим множество друзей друзей:
$$display$$\Gamma^{fof}(i) = \bigcup_{j \in \Gamma (i)} \Gamma (j) — \Gamma (i)$$display$$
2) и построим суб-графы $inline$\begin{align*} G^{fof}(i)\end{align*}$inline$ связей с друзьями и друзьями друзей, $inline$\begin{align*} \forall e (x, y) \in E, e (x, y) \in G^{fof}(i) \iff x, y \in \Gamma^{fof}(i) \cup \Gamma (i) \end{align*}$inline$
3) выделим множество вершин, $inline$\begin{align*} D_i: \{d_1, …, d_k \}\end{align*}$inline$, с которыми образовались связи — это наши позитивные примеры для обучения,
4) все неслучившиеся связи из множества $inline$\begin{align*} \overline{D_i} = \Gamma^{fof}(i) — D_i\end{align*}$inline$ — это наши негативные примеры для обучения.

Наша задача — подобрать такой вектор весов $inline$\begin{align*} \xi \end{align*}$inline$, при котором позитивные примеры из множества $inline$\begin{align*} D_i\end{align*}$inline$ получат более высокое значение Personalized PageRank относительно $inline$\begin{align*} i\end{align*}$inline$, чем негативные примеры.
Для этого зададим функцию потерь, которую будем минимизировать:
$$display$$ L = \sum_{i} \sum_{d \in D_i, \overline{d} \in \overline{D_i} } h (r_{\overline{d}} — r_{d}) + \lambda||\xi||^2,$$display$$
где $inline$h (x) = 0\iff x <0; h(x) = x^2 \iff x\geqslant 0;$inline$ — штраф за нарушение условия, $inline$\lambda$inline$ — сила $inline$L_2$inline$ регуляризации весов $inline$\xi$inline$, $inline$r$inline$ — вектор с решениями уравнения $inline$r = M^wr$inline$ относительно $inline$r$inline$ для суб-графа друзей друзей отдельно взятой вершины $inline$i$inline$.
Забавная деталь — градиент этой функции вычисляется так же, как и PageRank, степенным методом. Подробности — в 17-й лекции редакции 2014 года, слайды 9–27.
Вот так выглядело острие прогресса в момент моего первого знакомства с курсом cs224w.
А потом наступило торжество лени!
Известно, что теорию графов придумал Леонард Эйлер, когда ему наскучило решать нерешаемую задачу про те мосты, что стоят сейчас в Калининграде. Вместо того, чтобы голову сушить почём зря, он изобрёл математический аппарат, позволяющий доказать принципиальную невозможность решения головоломки.
В лучших традициях вычислительных наук, мы тоже будем лениться и зададимся задачей поиска функции, которая бы позволила отойти от одномерных представлений узлов и перейти к многомерным векторам свойств.

Здесь мы знакомимся с графовыми эмбеддингами в современном понимании этого термина.
Формально, мы хотим:1) Определить энкодер (функцию соответствия ENC, которая задаёт преобразование узла $inline$u$inline$ в вектор $inline$z_u$inline$);
2) Определить функцию подобия узлов (меру близости в графе, который мы будем подавать на вход энкодера);
3) Оптимизировать параметры энкодера таким образом, что:$$display$$similarity (u, v) \approx z_{v}^{T} z_v$$display$$
Мы стремимся к тому, чтобы вершины, близко расположенные в графе, получали близкое представление в векторном отображении. Другими словами, чтобы угол между двумя полученными векторами был минимален.
Здорово, а как её определить, эту близость в графе?
Например, будем считать, что вес ребра — хорошая мера близости и её можно приближенно считать равной скалярному произведению для эмбеддингов двух узлов. Функция потерь для такого случая примет вид:
$$display$$L = \sum_{(u, v) \in V \times V} || z_{u}^{T}z_v — A_{u, v}||^2,$$display$$
остаётся найти (например, градиентным спуском) матрицу $inline$Z \in \mathbb{R}^{d \times|V|}$inline$, которая минимизирует $inline$L$inline$.
Альтернативный подход — определить окружение $inline$N (v)$inline$ для вершины шире, чем множество соседей.

В этом нам помогут блуждания по графу. Первый проект, использовавший этот подход — DeepWalk. Суть метода заключается в том, что мы будем запускать бродягу гулять по графу случайным образом из каждой вершины $inline$v$inline$, и скармливать короткие последовательности фиксированной длины посещённых за время его прогулки вершин в word2vec.
Здесь интуиция состоит в том, что распределение вероятности посещения вершин графа — степенной закон — очень похож на распределение вероятности появления слов в человеческих языках. И раз word2vec работает для слов, то и для графов может. Попробовали — получилось!
В DeepWalk бродяга реализует марковский процесс первого порядка — из каждой вершины мы переходим в соседние, согласно вероятностям из взвешенной матрицы смежности $inline$M$inline$ (либо её производных, вроде $inline$M^w$inline$). То, откуда мы пришли в вершину — никак не влияет на выбор следующего шага.
Для того, чтобы реализовать блуждания, потребуется генератор псевдослучайных чисел и немножко алгебры. Самое время воспользоваться блоком для цитат по прямому его назначению.
«Всякий, кто соглашается с арифметическими методами генерации, разумеется, грешен. Как было неоднократно показано, нет такой вещи, как случайное число — есть лишь методы создания та



