Дерево отрезков: просто и быстро
Накануне очередного запуска курса «Алгоритмы для разработчиков» мы провели открытый урок. На нём поговорили об известной идее дерева отрезков, обсудили, как его строить, обновлять и быстро O(log n) вычислять сумму чисел любого отрезка данного массива. Алгоритм очень простой и экономный: нужно O(n) памяти. Для закрепления материала решили олимпиадную задачу.

Вебинар провёл опытный программист и преподаватель, а также руководитель курса «Алгоритмы для разработчиков» Евгений Волосатов.
Присказка
Дерево отрезков — это структура данных, которая позволяет алгоритмически просто и логарифмически быстро находить сумму элементов массива на заданном отрезке.
К примеру, представьте, что надо найти сумму следующих чисел:

При этом нам нужно не просто вычислить сумму чисел указанной последовательности (сумму элементов определённого массива), а максимально быстро найти сумму любой последовательности из этих чисел. То есть мы можем задать какой-нибудь интервал (отрезок) и максимально быстро дать ответ, чему равна сумма чисел из этого интервала:

Что значит быстро? Это значит быстрее, чем, если бы мы просто суммировали числа. Ведь чисел может быть и миллионы, и миллиарды…
Именно желание быстро находить сумму последовательных элементов и стало мотивацией нашего вебинара. Причём, речь идёт не только о сумме, но и о других задачах, например, вычислении любой ассоциативной функции. Таким образом, мы говорим об операциях, выполнение которых не зависит от порядка вычисления.
Возвратимся к нашему ряду:

Очевидно, что если мы хотим находить результат быстро, нужно посчитать некоторые суммы заранее. Первое, что приходит на ум, складывать попарно:

Теперь, если нужно найти сумму чисел, мы можем сделать это практически моментально. Например, чтобы найти сумму упомянутого выше отрезка, достаточно будет 13 прибавить к 9. Всё элементарно: для нахождения суммы четырёх чисел мы сложили только два.
Усложняем задачу:
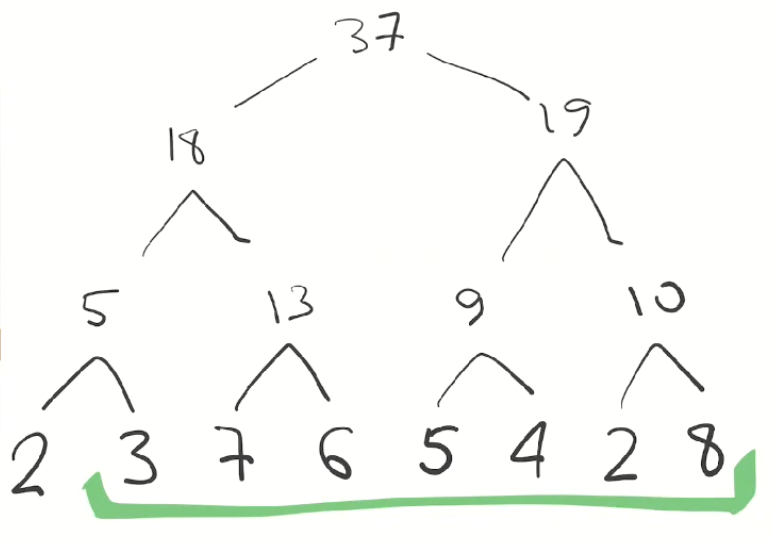
Чтобы найти сумму этого отрезка, нам нужно сложить элементы, которые, так или иначе, покрывают наш отрезок:

Разумеется, 3 + 13 + 19 = 35. Обратите внимание, чтобы найти сумму семи чисел, мы сложили только три. Если бы отрезок состоял из тысячи элементов, достаточно было бы сложить в среднем 10 элементов, так как мы имеем логарифмическую сложность с логарифмом по основанию 2. И это быстро!
Полное двоичное дерево
Полное двоичное дерево — это дерево, у каждого элемента которого есть ровно два дочерних элемента.
Для работы с полным двоичным деревом можно и нужно использовать такую структуру данных, как массив. Нумеровать этот массив удобно с единицы. Пронумеруем каждый элемент двоичного дерева натуральными числами от 1 до 2n-1:

Вся красота подхода в том, что очень легко вычислять номер детей и родителей.
Формула вычисления «левого ребёнка»: i*2, «правого»: i*2+1.

Например, вычислим номера детей у пятого элемента:
- 5×2 = 10;
- 5×2 + 1 = 11.
А как от «ребёнка» подняться к «родителю»? Используем целочисленное деление i / 2
Ок, а как определить, левый ребёнок или правый? Ответ следующий: у левых детей чётные номера, у правых — нечётные.
Запомним эти моменты.
Возвратившись к нашему примеру бинарного дерева, зададимся вопросом, как нам его построить? Смотрите, у нас вначале есть массив чисел:

Для него нужно построить двоичное дерево. Сколько потребуется памяти для хранения двоичного дерева, внизу которого находятся эти элементы?
Ответ на этот вопрос — 2n, если n является степенью двойки.
Идём дальше, ведь перед нами возникают ещё два вопроса:
- с какого элемента необходимо разместить исходные числа в массиве полного двоичного дерева?
- с какого элемента и в какую сторону мы начнём заполнять наше дерево предварительно рассчитанными суммами?

Ответить на первый вопрос достаточно просто: у нас 8 элементов, всего в массиве будет 16 элементов, значит, первый элемент будет под номером 16 — 8 = 8. И начинать строить мы будем слева-направо и снизу-вверх, начиная с 7 элемента, складывая значения у детей, вот так:

Далее необходимо определить, как именно находить сумму нужного отрезка. Вернёмся к нашему первому примеру, пронумеруем элементы и зададим отрезок, причём обозначим первый элемент в отрезке, который нужно сложить, буквой L, а последний — R:

Теперь необходимо ввести ещё одно понятие, чтобы был ясен алгоритм действий. Речь идёт о понятии фундаментальных элементов и соответствующих им фундаментальных отрезков. Фундаментальный элемент — это какой угодно элемент из всего массива, и ему соответствует фундаментальный отрезок, то есть те элементы из начального массива, которые являются его непосредственными детьми/внуками. Для фундаментального элемента с номером 4 »5» фундаментальный отрезок будет с 8 по 9 элемент: [»2»;»3»]:

Что касается фундаментального элемента с номером 10 — »7» (мы обозначили его L), он совпадает со своим фундаментальным отрезком. Можно ли расширить этот фундаментальный отрезок, не выходя за пределы L-R? В нашем случае можно. Правило для левой границы такое: если это левый ребёнок, то фундаментальный отрезок можно расширить, новый фундаментальный элемент будет являться родителем текущего. То есть мы можем в программе писать следующее:

Теперь перейдём к правому элементу R. Он является фундаментальным элементом и левым ребёнком, поэтому расширить область мы уже не можем (выйдем за пределы отрезка). Значит, можем добавить этот элемент к ответу:

Далее нужно, чтобы левый элемент двигался к правому, а правый — к левому. Для левого элемента с индексом L = 10 следующий индекс равен 5, т. к. он пойдёт к родителю. Но пойдёт сначала вправо, а потом вверх:

Итак, значение L перешло на уровень выше и немного правее. Как же будет уменьшаться R? С помощью формулы (R — 1) / 2.

Вот такой алгоритм. Что касается следующих значений переменных L и R, то далее они будут перемещаться следующим образом:

Если же в дереве будет не 8 элементов, а неудобное число, скажем 12, нам придётся дополнить дерево (двоичное дерево должно быть полным) до 16-ти.
Формула для вычисления количества элементов (берётся целая часть логарифма):

Теперь вычислим ассоциативную функцию нахождения минимума. Вот наше дерево и отрезок:

Как думаете, сколько раз в нашей функции будет задействован элемент № 5 — один или два? Разумеется, один, но каким образом это проверяется в алгоритме? На самом деле, этот элемент является либо левым, либо правым сыном, а значит, выполнится действие либо для L, либо для R.
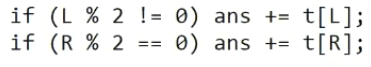
+
Теперь рассмотрим операцию изменения. Допустим, изменился какой-нибудь элемент, например, вместо 7 пришёл 0. Чтобы наше дерево отрезков осталось в рабочем состоянии, необходимо обновить всех родителей, причём нужно идти до самого верха.

Решение олимпиадной задачи
Одно из требований к таким задачам — всё должно работать быстро. Итак, имеем следующее условие:

Будем решать её, используя знания о дереве отрезков. В результате получим следующий код на C#:

Отправляем на проверку, видим, что решение принято и является полным, а значит, наш алгоритм работает.

На этом всё, если хотите подробностей, смотрите видео целиком. Также можете на досуге почитать следующие авторские статьи нашего преподавателя Евгения Волосатова на Хабре:
— Балансировка красно-чёрных деревьев — Три случая;
— Ход конём по битам. Шахматный Bitboard.
