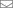Бардак в идеальном мире. Часть 229.07.2023 08:31

Это продолжение статьи про элементы теории хаоса с картинками. Современная теория хаоса — это большая и хорошо разработанная область математики, уже прочно вошедшая в набор современных инструментов естествознания. Многие результаты теории динамического хаоса, такие как странные аттракторы, бифуркационные диаграммы, фрактальные области притяжения, разобраны популяризаторами математики на плакаты, мемы и открытки. В этой мини‑серии статей я хочу копнуть немного глубже стандартных введений и «альбомов» с симпатичными картинками и дать пример разбора одной несложной, но ещё не «заезженной» механической системы, которая демонстрирует механизмы возникновения хаоса в гамильтоновых системах.

Мы разбираемся с движением идеального шарика, свободно падающего и упруго отскакивающего от столика на линейной пружинке. Главное достоинство этой системы состоит в том, что она позволяет продемонстрировать основные приёмы анализа хаотических систем, а главное, сделать видимыми возникающие при этом неочевидные математические структуры: инвариантные торы, резонансные циклы и разрушающиеся гомоклинические многообразия. Обычно в книгах и статьях их изображают схематично, здесь же у нас есть возможность увидеть их «истинный» облик.

В первой части мы увидели, какими необычно сложными могут быть подскакивания шарика над столиком с пружинкой. Движение самих тел достаточно тривиально, а вот их упругие соударения оказались способны производить красивую динамику, как упорядоченную, так и хаотичную. Рекомендую, если не прочитать первую часть, то хотя бы полюбоваться иллюстрациями, чтобы понять что именно мы будем объяснять на этот раз.

В физике под динамикой понимают движение некоторых тел или среды под действием сил, а более общем смысле — изменение состояния системы с течением времени. В математике понятие динамики ещё более абстрактное: это действие непрерывного гладкого отображения на некоторое гладкое многообразие. В нашем случае, многообразие — это пространство всех возможных состояний системы шарик-столик, которое описывается координатами и скоростями обоих тел, а действует на него отображение , заданное очень простыми уравнениями движения:

$\begin{align*}&\dot{p}_1=-1,\\&\dot{p}_2=-q_2,\\&p_1\leftrightarrow p_2,\quad \text{if}\quad q_1 = q_2. \end{align*}$

Здесь $q_{1,2}$ — безразмерные координаты шарика и столика, $p_{1,2}$ — их скорости, а точки обозначают производные по времени. Третья строчка определяет условие упругого соударения при котором происходит обмен импульсами между шариком и столиком и заключает в себе нелинейность задачи.

Для того чтобы избежать необходимости работать в четырёхмерном фазовом пространстве (q_1,p_1,q_2,p_2) и исключить явную зависимость от времени, мы сосредоточились на моментах соударений наших тел, когда q_1=q_2 . Так от отображения , непрерывного во времени, мы перешли к дискретному отображению $P:(q_1,p_1,p_2)_i\to(q_1,p_1,p_2)_{i+1},$ а потом упростили и его до отображения: $\Pi:(\varphi,\theta)_i\to (\varphi,\theta)_{i+1},$ которые называются отображениями Пуанкаре. Последнее отображение образует динамику на двумерной сферической поверхности, задаваемой законом сохранения энергии системы:

(q_1+1)^2+p_1^2+p_2^2 = 2E+1.

Здесь — это полная энергия системы. Это единственный параметр задачи, который определяется еë начальными условиями: начальной высотой и скоростью шарика и столика. Поскольку система консервативна (гамильтонова) энергия не изменяется и может служить параметром.

Замечание для тех, кто в теме

Как правило, при анализе гамильтоновых систем, рассматривают некоторую интегрируемую систему и вводят малое возмущение, из-за которого возникают нелинейные эффекты и хаос. Из-за упругих столкновений наша система интегрируема только в тривиальном случае — в покое, так что и выполняет роль параметра возмущения.

Таким образом, от уравнений движения мы перешли к дискретному отображению $\Pi$ , которое порождает последовательности соударений — орбиты отображения, и однозначно определяется единственным свободным параметром задачи . Семейства орбит, как выяснилось, могут выглядеть неожиданно красиво. На рисунке показан пример такого семейства для E=1 , изображенный в азимутальной проекции (детали построения такой проекции, смотрите в первой части).

Зелёной линией показана линия симметрии

Физическая симметрия задачи нашла отражение в симметрии фазового пространства и системы орбит. На азимутальной проекции выделяется зеркальная симметрия, с осью проходящей через начало координат и включающая в себя меридианы и (зелёная линия на рисунке). Напомню, что таким образом проявляется симметрия обмена скоростями при упругом соударении одинаковых по массе тел.

Путешествие вокруг полюса

Перед тем как приступать к исследованию хаоса, нам нужно детально рассмотреть все возможные типы регулярных орбит отображения $\Pi$ , их физический смысл и общую структуру. Эта часть рассказа необходима для того, чтобы познакомить нас с главными персонажами в гамильтоновом сценарии перехода к хаосу: полюсами и седловыми точками, эллиптическими и гиперболическими циклами, а также с инвариантными торами и гетероклиническими многообразиями.

Неподвижные точки

В прошлый раз мы отметили, что отображение $\Pi$ является гомеоморфизмом — непрерывным отображением сферической поверхности в себя. Существует топологический факт, известный как теорема Брауэра:

Любое непрерывное отображение замкнутого шара в себя в конечномерном евклидовом пространстве имеет неподвижную точку.

Из этой теоремы следует, что обязана существовать как минимум одна точка, которую отображение $\Pi$ возвращает в саму себя, то есть, неподвижная точка отображения Пуанкаре. По крайней мере, одну такую точку мы знаем: это точка со сферическими координатами Ей соответствует состояние покоя системы в равновесии.

Давайте поищем другие неподвижные точки преобразования $\Pi$ . В силу симметричности системы орбит преобразования, его неподвижные точки могут либо лежать на нулевом меридиане, либо располагаться зеркально относительно неё. Однако во втором случае обмен скоростями при ударе должен перевести любую такую точку в её зеркальное отражение, а значит, ни одна из них не останется неподвижной. Если мы ищем точки, переходящие сами в себя при зеркальном отражении относительно нулевого меридиана, то значит, все они должны лежать на нём.

Для того, чтобы найти все такие точки, вычислим расстояние между исходными точками нулевого меридиана и их образами:

Если хаос это отсутствие порядка, то перед тем, как постигать хаос, стоит разобраться с тем, как устроен порядок. Продолжаем наш неспешный разговор об элементах теории хаоса.-4

Видим, что нулю это расстояние равно только в точках равновесия $\mathbf{p}^0$ , и в точке $\mathbf{p}^1$ , выглядящей как полюс вокруг которой располагаются всё прочие орбиты. Других неподвижных точек в системе нет.

Точке $\mathbf{p}^1$ соответствуют абсолютно правильные периодические подпрыгивания шарика, в которых в точности повторяются и координата соударения и скорости тел, равные друг другу по модулю в момент удара.

Движение шарика (голубая линия) и столика (оранжевая линия), соответствующее неподвижной точке — орбите p¹.

Движение шарика (голубые параболы) и столика (оранжевые синусоиды), соответствующее неподвижной точке — орбите p¹.

Полюс и его окрестности

Точка $\mathbf{p}^1$ окружена сплошными кольцеобразными орбитами-спутниками. Давайте рассмотрим её окрестности подробнее:

Происходящее очень похоже на фазовый портрет для колеблющегося маятника. Это значит, что если немного «промазать» мимо неподвижной точки то должны наблюдаться своего рода колебания вокруг неё. Рассматривать физические траектории тел тут смысла мало, наш глаз не заметит разницы. Вместо этого, мы прибегнем к математическому анализу.

В прошлый раз мы подметили гладкость отображения $\Pi$ , это значит, что его можно воспринимать, как гладкую вектор‑функцию и, следовательно, раскладывать в степенные ряды. Давайте рассмотрим линейное приближение отображения вокруг неподвижной точки. Для обыкновенной функции еë линейное поведение около неподвижной точки x_0 выглядело бы как прибавление к неподвижной точке величины ∆y = f'(x_0) ∆x :

$f(x_0+∆x) \approx f(x_0) +f'(x_0) \Delta x =\\=x_0+f'(x_0) \Delta x=x_0+\Delta y.$

Для нашего отображения, как для функции над векторами, линейное поведение около неподвижной точки будет выражено очень похожим образом, но вместо прибавления числовой величины, мы будем немного смещаться от исходной точки на малый вектор $\Delta \mathbf{x}$ , а образ смещения будет выражаться новым вектором $\Delta\mathbf{y}$ :

$\Pi(\mathbf{p}^1) \approx \mathbf{p}^1+J(\mathbf{p}^1)\Delta x =\mathbf{p}^1+\Delta y.$

Смещение образа можно выразить, как результат действия на $\Delta \mathbf{x}$ некоторой матрицы $J(\mathbf{p}^1)$ . Она называется матрицей Якоби или якобианом отображения и представляет его линейное приближение в некоторой точке, подобно тому, как производная является линейным приближением функции . Собственно, якобиан и вычисляется через частные производные от компонентов вектор-функции, но, увы, нам неведомо явное выражение для $\Pi$ , мы знаем только алгоритм его вычисления. Однако, гладкость этого отображения позволяет нам вычислять производные численными методами.

Чтобы понять, что происходит с фазовым пространством вокруг точки $\mathbf{p}^1$ , посмотрим как действует отображение $\Pi$ на два небольших ортогональных вектора, исходящих из неё.

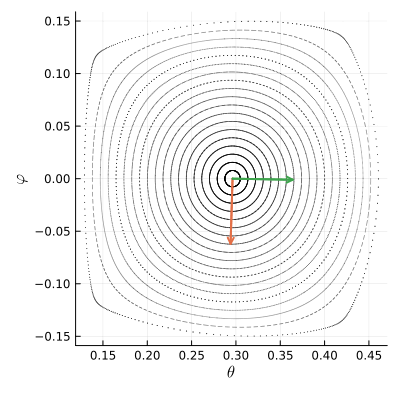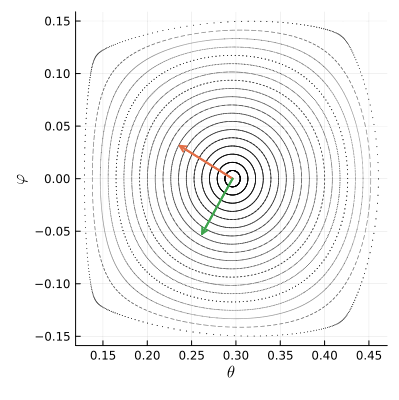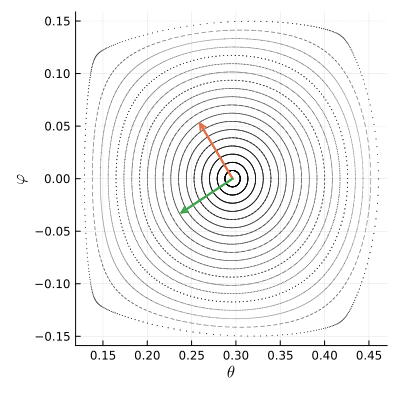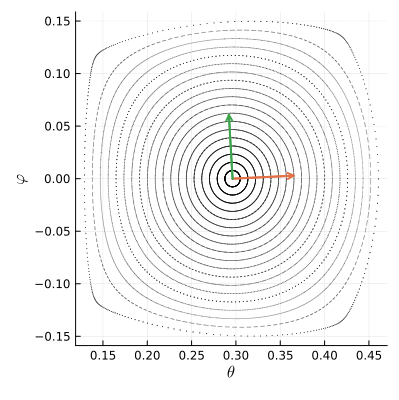
Результат многократного применения отображения П к двум малым векторам. Векторы были выбраны очень маленькими, но потом я их пропорционально увеличил, чтобы они стали хорошо видны.

Результат многократного применения отображения $\Pi$ при E=1

к двум малым векторам. Векторы были выбраны очень маленькими, но потом я их пропорционально увеличил, чтобы они стали хорошо видны.

Как видим, отображение поворачивает векторы по часовой стрелке на четверть оборота и ещё чуть-чуть доворачивает. Численное вычисление производных $\Pi$ в неподвижной точке показывает, что на малые векторы действует такая матрица Якоби:

$J(\mathbf{p}^1) = \begin{pmatrix}-0.0242703& -3.02759\\0.330101& -0.0242702\end{pmatrix}.$

Важную информацию о преобразовании несут определитель и спектр матрицы Якоби, то есть множество её собственных чисел. Определитель якобиана показывает, как под действием преобразования меняется площадь фигур. Для полученной нами матрицы он равен единице. Это значит, что преобразование сохраняет объём фазового подпространства, в котором мы работаем. Собственные числа якобиана получились комплексными: $\lambda_{1,2} = -0.0242702 \pm 0.9997054i$ и их модуль тоже равен единице. Всё это говорит о том, что в точке $\mathbf{p}^1$ отображение $\Pi$ ведёт себя, как поворот, не изменяющий объёма пространства вокруг неподвижной точки.

Угол поворота, который совершает окрестность полюса под действием отображения, можно вычислить через аргумент собственного числа якобиана, в нашем случае он оказывается равным $91.4^\circ$ — те самые четверть оборота и ещё чуть-чуть, что мы наблюдали в эксперименте. Неподвижные точки, вокруг которых происходит вращение пространства, называют полюсами или эллиптическими точками. Собственные числа якобиана в таких точках должны лежать на единичной комплексной окружности, и иметь ненулевую мнимую часть.

Циклы и седловые точки

На портрете отображения видны и другие семейства концентрических эллиптических орбит, которые тоже образуются вокруг некоторых особых точек. Эти точки неподвижны для отображения $\Pi$ , применённого несколько раз. Яркий тому пример дают четыре крупные кольцевые структуры, расположенные вокруг полюса $\mathbf{p}^1$ . Вот как они выглядят вблизи:

Синие стрелки показывают как особые точки переходят друг в друга под действием П.

Точки, обозначенные на рисунке, как $\mathbf{p}^4$ , под действием отображения $\Pi$ переходят друг в друга по очереди. При этом отображение $\Pi^4(x) = \Pi(\Pi(\Pi(\Pi(x))))$ переводит каждую из них в саму себя. Такие точки образуют периодические орбиты или циклы. Полюсы, составляющие цикл конечной длины мы будем называть полюсами -ного порядка и обозначать $\mathbf{p}^n.$

В том, что это именно полюсы можно убедиться, вычислив спектр якобиана от $\Pi^4$ для них (они комплексные, лежат на единичной окружности и их аргумент соответствует повороту на $-1.37^\circ$ либо наблюдая действие этого отображения на малые векторы.

Обратите внимание на направление и фазу, вращения пространства вокруг точек $\mathbf{p}^4$ , а также на то, что $\Pi^4$ , действуя на окрестности $\mathbf{p}^1$ оставляет только сумму небольших доворотов, так что вращение становится плавным.

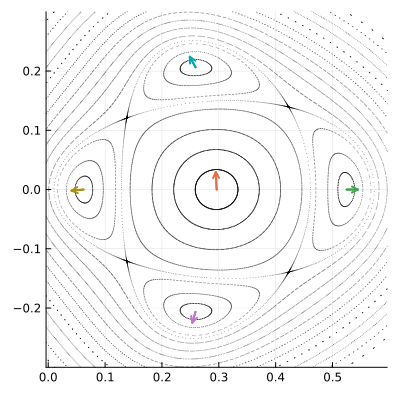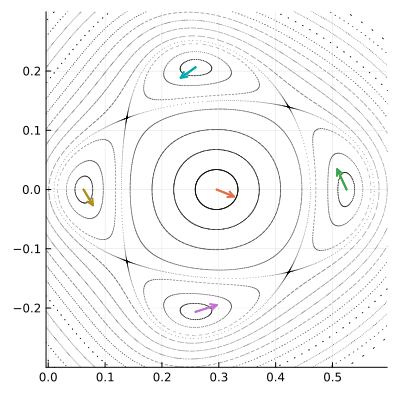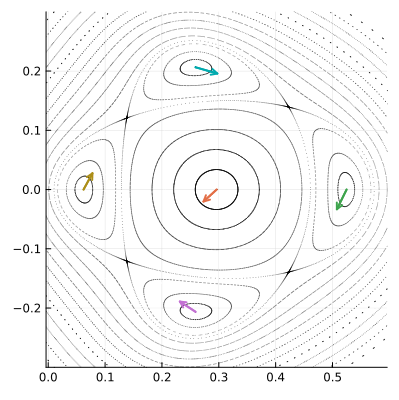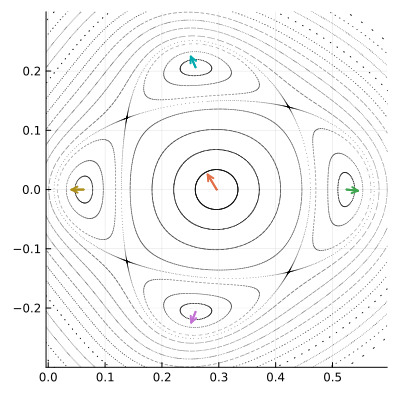
Однако несколько полюсов не могут размещаться рядом, не смыкаясь орбитами-спутниками. В какой-то точке эти орбиты должны будут соприкоснуться. Мы говорили, что в автономных системах, типа нашей, фазовые траектории пересекаться не могут, за исключением особых случаев. Это как раз такой случай. Особые точки, в которых разные орбиты пересекаются, тоже будут неподвижными для $\Pi^n$ , они называются седловыми или гиперболическими точками. Мы будем обозначать их $\mathbf{s}^4$ . Показанные на рисунке точки $\mathbf{s}^4$ тоже образуют цикл четвёртого порядка, но он существенно отличается от цикла, образованного полюсами, динамикой фазового пространства в окрестности составляющих его точек.

Давайте исследуем их локальное поведение, наблюдая за тем, как отображение $\Pi^4$ действует на два малых ортогональных вектора, исходящих из точки пересечения орбит, вдоль их касательных.

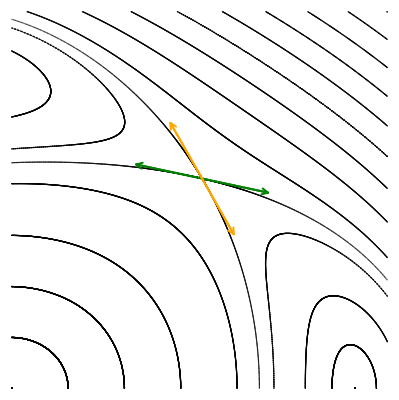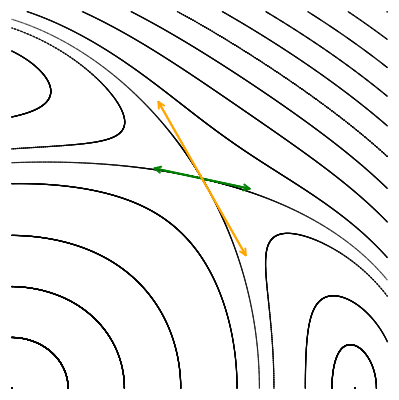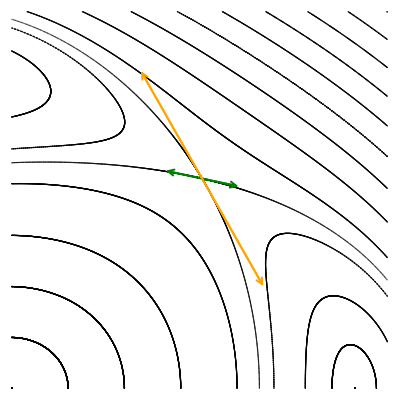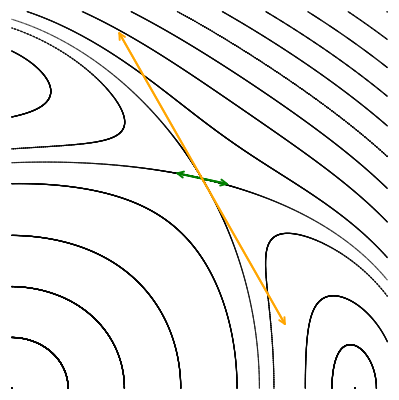
Опять мы преобразовываем малые векторы, но для того чтобы их можно было увидеть, они пропорционально увеличены.

Мы видим, что по действием отображения Пуанкаре векторы не поворачиваются, а меняют свою длину: одна пара вытягивается, а другая сжимается. Выбранные нами направления совпадают с направлением собственных векторов якобиана в гиперболической точке. Действие матрицы на собственный вектор выражается только в умножении его на собственное число, без всякого поворота. Это значит, что собственные числа якобиана гиперболической точки должны быть вещественными. Причём наблюдаемая нами динамика говорит о том, что одно собственное число по модулю должно быть больше единицы (вектор удлинняется), а другое — меньше единицы, соответствующий собственный вектор укорачивается.

Для седловой точки $\mathbf{s}^4$ при E=1 якобиан получилcя таким:

$J(\mathbf{p}^1) = \begin{pmatrix}1.1292 & 0.298841\\-0.0216436& 0.879855\end{pmatrix}$

с собствеными значениями: $\lambda_1=1.09979, \lambda_2 = 0.909264.$ Примечательно, что для нашей системы определитель якобиана в этой точке равен единице, также как и в полюсе. То есть, не смотря на существенное искажение окрестностей фазового пространства, гиперболическое поведение не изменяет никакие площади.

Таким образом, мы приходим к важному заключению: циклы могут состоять либо из полюсов, либо из гиперболических точек. В первом случае орбита будет находиться в цикле или в его окрестности неограниченно долго. Такие устойчивые циклы мы назовём эллиптическими. Во втором случае при сколь угодно малом отклонении от седловой точки орбита покинет еë и вернется обратно, только пройдя по некоторой замкнутой линии, удаляясь от от исходной точки очень далеко. И седловые точки и образуемые ими гиперболические циклы являются неустойчивыми.

Инвариантные торы

А из чего состоят многочисленные орбиты, окружающие наши особые точки? Они выглядят, как сплошные замкнутые линии, можно ли воспринимать их как циклы очень высокого порядка? Для того чтобы понять, что же эти орбиты собой представляют, нам надо вернуться в четырёхмерное фазовое пространство (q_1,q_2,p_1,p_2) . Исследуемое нами дискретное отображение $\Pi$ получается сечением непрерывных траекторий гиперплоскостью q_1=q_2, в которой лежат точки соударения.

Давайте посмотрим как выглядит фазовая траектория для неподвижной точки $\mathbf{p}^1$ в подходящем сечении четырёхмерного фазового пространства:

Это петля, которая встречает сечение Пуанкаре в неподвижной точке, потом покидает сечение и вновь возвращается к нему. А вот как выглядит фазовая траектория для цикла четвёртого порядка:

Обе траектории представляют собой нормальные замкнутые петли. Теперь построим траектории, соответствующие орбитам-спутникам этих неподвижных точек:

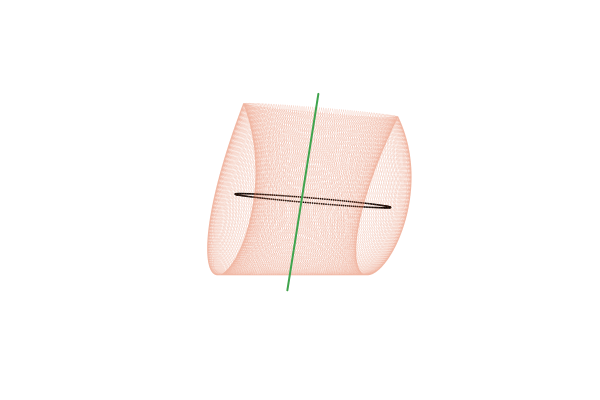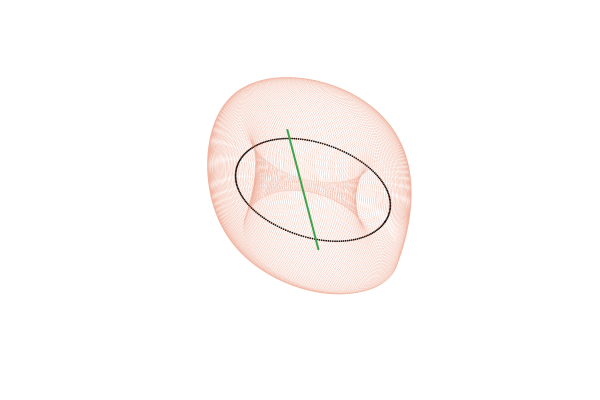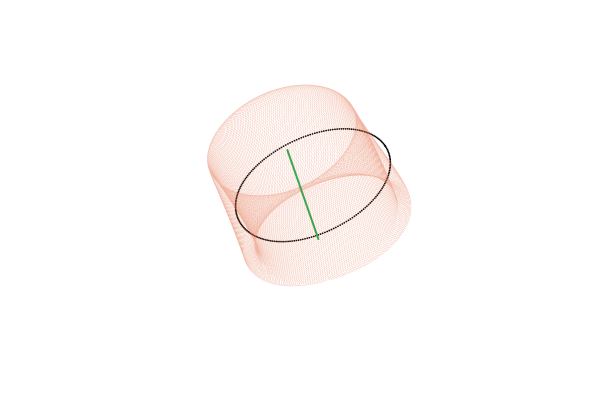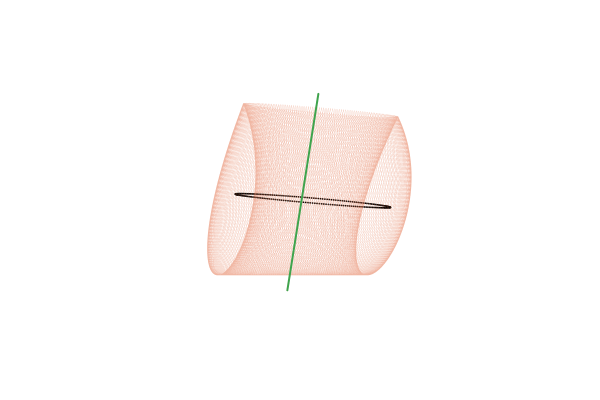
Мы видим, что полученные траектории «наматываются» на поверхности похожие на трубку, а сечение Пуанкаре вырезает на этой поверхности замкнутые кольцеобразные орбиты. Эти трубки особым образом замыкаются и образуют тор, внутри которого располагается петля цикла.

Обычно, говоря о торе, мы воображаем поверхность бублика. Чтобы получить из привычного тора наш вариант, нужно разрезать его и склеить, допустив самопересечение, как показано на рисунке:

С точки зрения топологии такой тор ничем не отличается от привычного. Чтобы получить тор для окрестностей цикла четвёртого порядка, его надо разрезать и переклеить четыре раза. Полюбуйтесь как выглядит небольшое семейство таких тороидальных трубок:

В отличие от циклов, траектории, образующие торы, не замкнуты и плотно заполняют тороидальную поверхность, не оставляя на ней ни одной точки, через которую не проходила бы траектория. Это значит, что в качестве решения задачи имеет смысл рассматривать весь тор сразу. Поскольку все его точки принадлежат одной бесконечной траектории, то исходная система уравнений переводит весь такой тор в себя. Таким образом, он является инвариантным многообразием динамической системы, а сечения тора — замкнутые орбиты, будут инвариантными многообразиями отображения Пуанкаре. Инвариантные торы называют также торами Колмогорова-Арнольда-Мозера, или КАМ-торами.

Теперь мы готовы исчерпывающе описать регулярную структуру фазового пространства задачи. Оно плотно заполнено одномерными замкнутыми петлями, и двумерными инвариантными торами, которые образуют расслоение пространства. Фазовое пространство отображения Пуанкаре, в свою очередь, содержит одномерные полюсы и седловые точки, образующие циклы, и расслаивается одномерными инвариантными многообразиями, которые мы тоже будем называть КАМ-торами.

Кроме перечисленных выше и хаотических, иных орбит в гамильтоновых системах нет. Так что рассмотреd все типы инвариантных многообразий и для нашего прыгающего шарика, мы познакомились со всем, что может встретиться и во всех других гамильтоновых механических системах: бильярдах на кривом столе, двойном или эластичном маятнике, в динамике атмосферы Юпитера или колец Сатурна.

Гидродинамика инвариантных торов

«Инвариантный» означает — неизменный. В нашем случае, речь идёт о том, что под действием уравнений движения одни точки этих многообразий переходят в другие, но при этом само многообразие (тор или петля) не изменяется и отображается уравнениями движения в себя. Таким образом, мы можем не заботиться о начальных условиях и рассматривать судьбу и свойства инвариантных многообразий, как неделимых объектов. То же относится и к орбитам отображения Пуанкаре: неподвижным точкам и сечениям КАМ‑торов.

Как мы увидели, в середине любого инвариантного тора «живёт» полюс, вокруг которого происходит вращение фазового пространства. Это значит, что точки торов, плотно заполняющих это пространство, сами тоже должны вращаться, оставляя сами торы на месте. На это движение моожно посмотреть.

Сегодня не будет формул, зато мы сделаем неожиданный поворот в нашем сюжете и от динамики инвариантных торов обратимся к облакам и развевающемуся флагу.-2

Движение отдельных точек на инвариантных торах под действием отображения $\Pi^4$ .

Обратите внимание, на каждом торе скорость движения точек своя, немного отличающаяся от скорости движения на соседнем торе. Это важное наблюдение подводит нас к неожиданной аналогии с движением сплошной среды.

В течении жидкости или газа на дозвуковых скоростях важную роль играет неразрывность среды. Она приводит к непрерывности и гладкости поля скоростей: у частиц, движущихся вдоль близких линий тока скорости тоже должны быть близки, а в пределе они должны гладко приходить друг к другу.

Если по какой-то причине наблюдается разрыв в скоростях соседних линий тока, то течение становится неустойчивым. При этом на границе развиваются волны, быстро превращающиеся в дорожку из вихрей, которые вращаясь, сглаживают разрыв, как подшипники. Этот механизм называется неустойчивостью Кельвина-Гельмгольца и наблюдается в жидкостях и газах

Развитие неустойчивости Кельвина-Гельмгольца в симуляции.

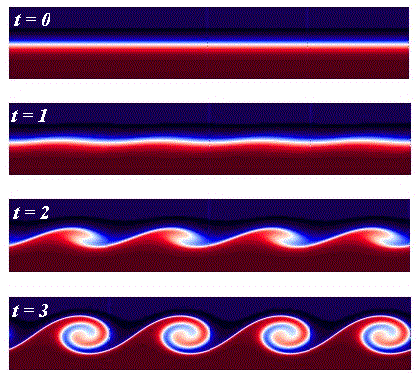
Отдельные этапы формирования вихревой дорожки.

Вихревая дорожка в небе

Ещё один пример неустойчивости Гельмгольца в природе.

Отображение Пуанкаре для нашей задачи имеет мало общего с гидродинамическим потоком: в нём нет инерции или давления. Объединяет эти два объекта только непрерывность поля скоростей и малые потери энергии (гамильтоновость). Эти ключевые характеристики приводят к тому, что они способны порождать подобные геометрические структуры.

Можно построить непрерывное поле скоростей, образованное инвариантными торами и увидеть, что при приближении к окрестностям неподвижных гиперболических точек движение орбит по разные стороны от седла происходит в противоположные стороны:

Сегодня не будет формул, зато мы сделаем неожиданный поворот в нашем сюжете и от динамики инвариантных торов обратимся к облакам и развевающемуся флагу.-4

Более того, это движение приводит к растяжению и сжатию пространства вдоль собственных векторов, которое мы наблюдали в окрестности седловой точки. В то же время, движение вокруг полюсов четвёртого порядка согласуется с общим движением потока и подобно вихрям Гельмгольца выполняет роль «подшипников», вращающихся без проскальзывания между внутренней областью, вращающейся по часовой стрелке, и внешней, которая вращается в противоположном направлении.

Получается, что по какой‑то причине в поле скоростей инвариантных торов образуется разрыв. Но поскольку непрерывность — ключевое свойство этого поля, то в нём формируется система из чередующихся полюсов и седловых точек, обеспечивающих сохранение этого свойства. Если вы ещё раз присмотритесь к тому, как развивается неустойчивость Кельвина-Гельмгольца, то без труда найдёте в течении невидимые седловые точки, которые легко распознаются по гиперболическому характеру поля скоростей вокруг них.

Ещё раз подчеркну: аэродинамические вихревые дорожки и инвариантные торы отображения Пуанкаре — явления абсолютно разной природы. Первое может служить аналогией второму только вследствие общих свойств гладких непрерывных преобразований. Это хорошо известное явление конвергенции, когда разные процессы приводят к одинаковым геометрическим формам. Ровно такие же паттерны и соображения вы можете встретить в теории полей, в решениях однородных дифференциальных уравнений, в теории аналитических функций, в общей топологии, везде, где непрерывность играет существенную роль. В этом и состоит очарование и сила математики!

Сходство динамики инвариантных торов и гидродинамических вихрей, естественно привлекло внимание механиков, исследовавших явление турбулентности и переход от ламинарного (слоистого) течения, в котором силы вязкости существенно превышают силы инерции, к когерентным структурам (крупных вихревым дорожкам) и потом к развитой турбулентности и к хаосу, когда система становится гамильтоновой и вязким трением на крупных масштабах можно пренебречь. Одними из первых, кто решил, что в динамике инвариантных торов можно найти сценарий перехода были А. Пуанкаре, Л. Ландау и А. Колмогоров. Однако позже, с дальнейшим развитием теории хаоса, стало ясно, что динамика инвариантных многообразий может служить лишь триггером к более сложным динамическим процессам — сценарию Рюэля и Такенса, диффузии Арнольда и другим явлениям.

Числа вращения и резонансы

Но что же останавливает вращение инвариантных торов? И почему для E=1 это привело к образованию двух циклов именно четвëртого порядка?

Существование неподвижных точек позволяет торам сменить направление вращения без нарушения непрерывности поля скоростей, но ценой образования дополнительной структуры: цепочки полюсов, окружённых замкнутыми орбитами, и раздёляющих их седловых точек. Но откуда берётся эта смена направления?

С точки зрения топологии, тор представляет собой произведение двух окружностей: $T = S^1\times S^1.$ Или, менее формально, это поверхность вращения, получаемая при движении окружности вокруг некоторой внешней оси. Под окружностями в топологии понимается произвольная замкнутая петля, а не только та правильная геометрическая фигура, которую мы проходили в школе. Поскольку тор мы понимаем достаточно обобщённо, вместо образующих его окружностей имеет смысл рассматривать две оси, которые охватывают эти петли: внутреннюю и внешнюю.

Внутренняя (чёрная) и внешняя (зелёная) оси одного из инвариантных торов, рассчитанных для E=1 в проекции (x + y, ẋ + ẏ, ẋ – ẏ) .

Внутренняя (чёрная) и внешняя (зелёная) оси одного из инвариантных торов,
рассчитанных для E=1

в проекции (q_1+q_2, p_1+p_2, p_1-p_2).

Действие отображения на инвариантный тор можно представить как композицию двух смещений вдоль образующих его петель. При этом в сечении Пуанкаре мы видим смещение только по одной из них, которое и воспринимаем как движение, похожее на вращение. По второй образующей фазовая траектория проходит во время между моментами пересечения плоскости q_1=q_2 , то есть, между столкновениями шарика и столика. Таким образом, траектория отображения как бы наматывается на тор по винтовой линии, как показано на рисунке:

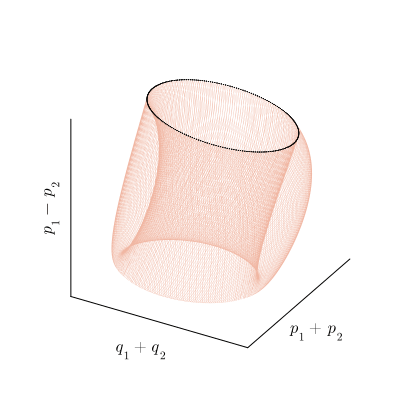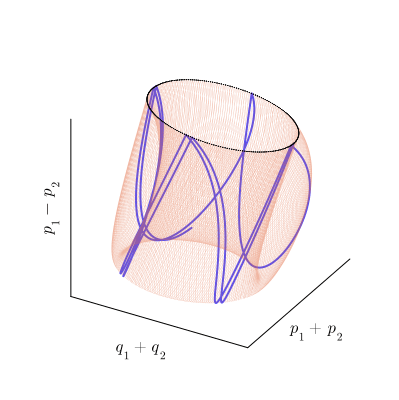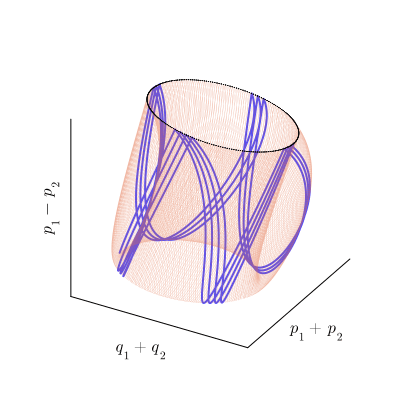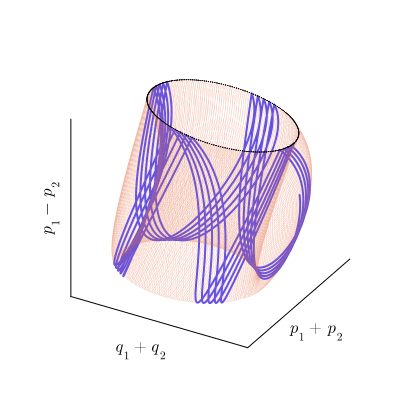
Расчетная фазовая траектория, образующая тор (синяя линия) и еë сечение Пуанкаре (чёрные точки).

Расчётная фазовая траектория, образующая тор (синяя линия) и еë сечение Пуанкаре (чёрные точки).

По мере этого наматывания, траектория совершает обороты вокруг обеих осей тора. Мы можем подсчитывать число оборотов, совершаемых траекторией вокруг каждой из осей тора и вычислять соотношение, показывающее сколько оборотов вокруг внутренней оси приходится на один оборот вокруг внешней. Это число называется числом вращения инвариантного тора. Обратите внимание на то, что эта числовая характеристика является чисто топологической и не меняется при непрерывных искажения