[Перевод] Шум Перлина22.11.2017 08:33

Я использовал шум Перлина для создания эффекта тумана и главного экрана в Under Construction. Я твитнул о моих усилиях по оптимизации алгоритма, и несколько людей ответили, что они не понимают, как работает шум Перлина и что это на самом деле такое.

Признаюсь, что я (немного) понимаю шум Перлина прежде всего потому, что я реализовывал его ранее, и несколько дней ушло на погружение в неуклюжие объяснения полдюжины разработчиков, более заинтересованных в показе собственных демок, нежели в реальном объяснении. Несколько полезных ресурсов, которые я нашел, часто содержали ошибки и не давали мне интуитивного чувства понимания, как и почему оно все-таки работает.

Что такое шум Перлина

В бытовом смысле, «шум» — это случайный мусор. Вот немного пиксельного шума.

Это белый шум. Грубо говоря, это означает, что все пикселы случайны и независимы друг от друга. Усредненное значение цвета для этих пикселов должно быть #808080, серый цвет — для этой картинки оно равно #848484, что довольно близко.

Шум полезен для генерации случайных шаблонов, особенно для непредсказуемых природных явлений. Изображение выше может быть хорошей начальной точкой для создания, например, текстуры гравия.

Однако большинство вещей не чисто случайны. Дым, облака, ландшафт могут иметь некий элемент случайности, но они были созданы в результате очень сложных взаимодействий множества крохотных частиц. Белый шум содержит независимые частицы (или пиксели). Для генерации чего-то более интересного, чем гравий, нам нужен другой вид шума.

Зачастую этот шум — шум Перлина, который выглядит вот так:

Надеюсь, что вам знакома эта картинка, пусть даже и как результат работы соответствующего фильтра в Photoshop. (Я создал его в GIMP, используя меню Filters → Render → Clouds → Solid Noise.)

Наиболее очевидное различие — картинка выглядит «облачной». Если говорить о технических деталях, она непрерывна — если сильно увеличить ее масштаб, градиент всегда будет плавным. Нет резких переходов от чёрного к белому, поэтому алгоритм работает на удивление хорошо, когда нужно что-то «случайное», но не слишком. Вот небо, которое можно быстро сделать из той же самой картинки:

Всё, что я сделал — добавил нижний слой голубого цвета и использовал уровни для вырезания самых тёмных частей шума. Можно было сделать и лучше, но для десяти секунд работы и так сойдёт. Этим изображением можно даже бесшовно замостить плоскость!

Шум Перлина с нуля

Вы можете создать шум Перлина в любом количестве измерений. Изображение выше, конечно, двумерное, но гораздо легче объяснить в одном измерении, где только один вход и один выход. Можно легко проиллюстрировать объяснение на обычном графике.

Для начала выберем для каждого целого числа $x = 0, 1, 2, 3, …,$ случайное вещественное из диапазона $[-1; 1]$ . Это будет наклон (тангенс угла наклона) прямой, проходящей через данную точку на числовой оси, которую я нарисовал голубым цветом:

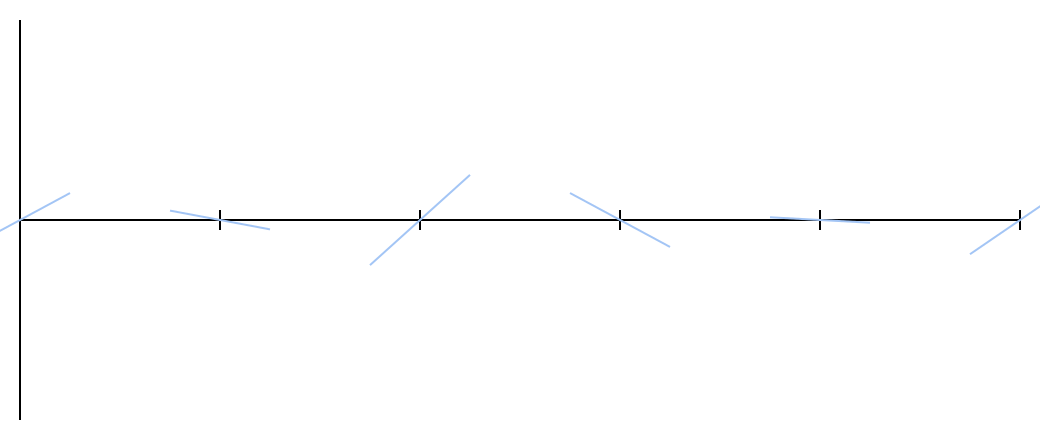
Неважно, сколько точек вы выберете. Каждый сегмент — пространство между двумя точками с засечками — будет обработан одним и тем же способом. Пока вы можете запоминать углы наклона прямых, можно продолжать ставить засечки в обе стороны числовой оси. Этих прямых достаточно, чтобы создать шум Перлина.

Каждый $x$ лежит между двумя засечками и, следовательно, между двумя прямыми. Пусть прямые имеют наклоны $a$ и $b$ . Уравнение прямой можно записать как $y=m(x-x_0)$ , где $m$ — наклон,
$x_0$ — значение $x$ , где прямая пересекает ось абсцисс.

Вооружившись этим знанием, легко найти, где эти две прямые пересекают заданный $x$ . Для простоты я предположу, что левая засечка находится в $x=0$ , а правая в $x=1$ ; это даст точки $ax$ и $b(x - 1)$ .

Я нарисовал пачку оранжевых точек для примера. Можете увидеть, как они продолжают две наклонные линии с каждой стороны.

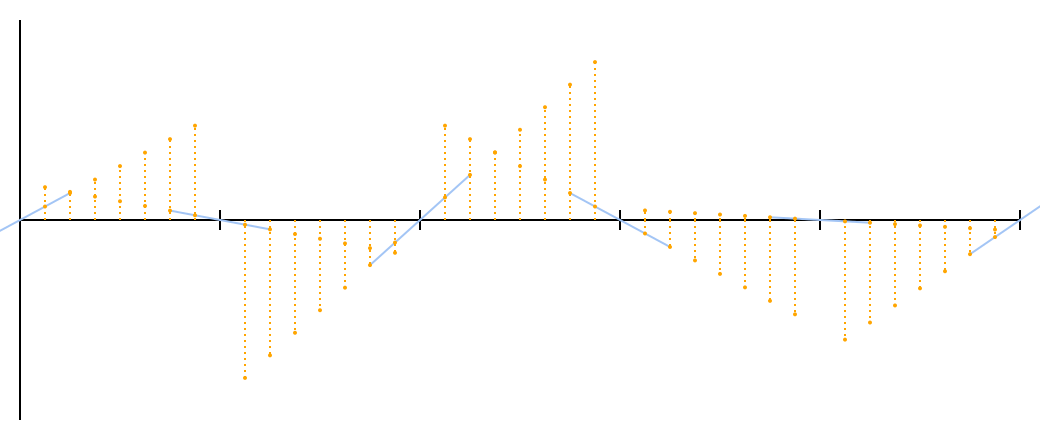
Теперь возникает вопрос: как можно эти пары точек для каждого $x$ превратить в гладкую кривую? Наиболее очевидный ответ — усреднить их, но беглый взгляд на график показывает, что такой подход не работает. «Среднее» двух прямых — это просто прямая с усреднённым наклоном, проходящая через точку пересечения, и отрезок этой прямой для каждого такого сегмента даже не будет касаться аналогичного отрезка в соседнем сегменте.

Нам нужен способ увеличивать вклад левого конца в «среднее» для точек, более близких к нему, и уменьшать этот вклад, когда мы ближе к правому концу. Самый простой способ сделать это — линейная интерполяция.

Линейная интерполяция предельно проста: если вы находитесь в точке $t$ на пути из $A$ в $B$ , линейная интерполяция будет равна $A + t(B - A)$ , что эквивалентно $A(1 - t) + Bt$ . Для $t = 0$ , вы получите $A$ ; для $t = 1$ , вы получите $B$ ; для $t = ½$ , вы получите $½(A + B)$ , среднее арифметическое.

Давайте попробуем это. Я обозначил интерполированные точки красным.

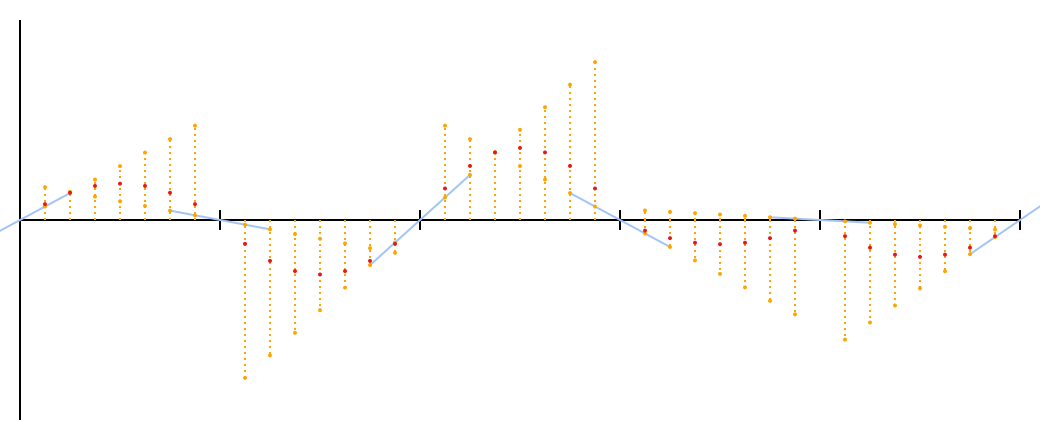
Неплохо для начала. Это ещё не шум Перлина; есть одна маленькая проблема, которая может не сразу бросаться в глаза при виде этих точек. Я могу сделать ее более видимой, если вы простите мне краткое отступление.

Каждая из этих кривых — парабола, заданная уравнением $y=(a - b)(x - x²)$ . Я хотел иметь возможность нарисовать параболы точно, нежели аппроксимировать их точками, то есть, разобраться, как изобразить параболы при помощи кривых Безье.

Кривые Безье — это те же самые кривые, которые вы используете для рисования путей в векторных графических редакторах вроде Inkscape, Illustrator или Flash. (Или в векторном формате SVG, который я использовал для создания всех этих иллюстраций.) Вы можете выбрать начальную и конечную точки, и программа отобразит дополнительные «ручки», прикреплённые к каждой точке. Перетаскивание этих «ручек» изменяет форму кривой. Это кубические кривые Безье, которые так называются из-за того, что на самом деле являются кривыми третьего порядка, но в принципе возможно нарисовать кривую Безье любого порядка.

При изучении математики кривых Безье я узнал несколько интересных вещей:

SVG поддерживает квадратичные кривые Безье! Это удобно, поскольку у меня квадратичные функции.
Кривые Безье задаются повторной линейной интерполяцией! На самом деле есть даже такая штука, как линейная «кривая» Безье — прямая линия между двумя заданными точками. Квадратичная кривая Безье имеет три опорные точки; вы линейно интерполируете между первой/второй и второй/третьей точками, затем интерполируете между этими двумя новыми точками. Кубическая кривая Безье имеет четыре опорные точки и делает на одну итерацию больше, и так далее. Поразительно.
Параболы, проходящие через красные точки, очень легко нарисовать при помощи кривых Безье — на самом деле шум Перлина имеет поразительное сходство с кривыми Безье! Этому даже есть некоторое объяснение. На первом шаге мы получаем значения и , что можно записать в виде , и это напоминает линейную интерполяцию. На втором шаге идёт самая что ни на есть линейная интерполяция. А два раунда линейной интерполяции — это по определению кривая Безье второго порядка.

Думаю, у меня есть геометрическая интерпретация того, что же на самом деле происходит.

Рассмотрим сегмент. У него есть лучи (половинки прямых), выходящие из его концов и направленные к центру сегмента. Отразите их относительно середины сегмента, получив таким образом еще по одному лучу на каждом конце. На каждом конце сложите наклоны лучей и получите два новых луча; они являются зеркальным отражением друг друга относительно середины сегмента, поскольку получены из суммы исходного луча и отражения другого. Наконец нарисуйте кривую между этими лучами.

Ниже я проиллюстрировал эти действия. Пунктирные линии — отраженные лучи; синие — лучи, полученные после суммирования; синие точки — их пересечения (и третья опорная точка квадратичной кривой Безье); красная дуга — точная кривая, проходящая через красные точки. Если вы знаете основы дифференциального исчисления, вы можете убедиться, что наклон левого луча равен $a - b$ , наклон правого луча равен $b - a$ , и это действительно указывает на их симметрию относительно центра сегмента.

Надеюсь, теперь проблема более очевидна: эти кривые не переходят друг в друга плавно.
В каждой засечке ясно виден излом. Тот излом, где обе кривые смотрят вниз, особенно плох.

Линейная интерполяция, как выясняется, недостаточна. Даже если мы слишком близко к одному концу, другой всё ещё имеет значительное влияние, которое оттопыривает кривую от исходной случайной направляющей. Это влияние должно угасать более резко на концах сегментов.

К счастью, кто-то уже выяснил это за нас. До того, как мы делаем линейную интерполяцию,
мы можем сместить $t$ при помощи функции smoothstep. Это s-образная кривая, похожая на диагональную прямую $y = x$ , но сплющенная в нуле и единице. В середине она не очень сильно меняется — $½$ остаётся $½$ —, но она сильно смещает концы. В точке $0.9$ она равна $0.972$ .

Полученная кривая имеет четвертую степень, что не позволяет её точно отрисовать в SVG при помощи нативных кривых Безье, поэтому серая линия — это грубая аппроксимация. Я компенсировал это добавлением большого количества точек, которые имеют чёрный цвет. Между прочим, эти точки получены из оригинальной функции Кена Перлина noise1; это настоящий шум Перлина.

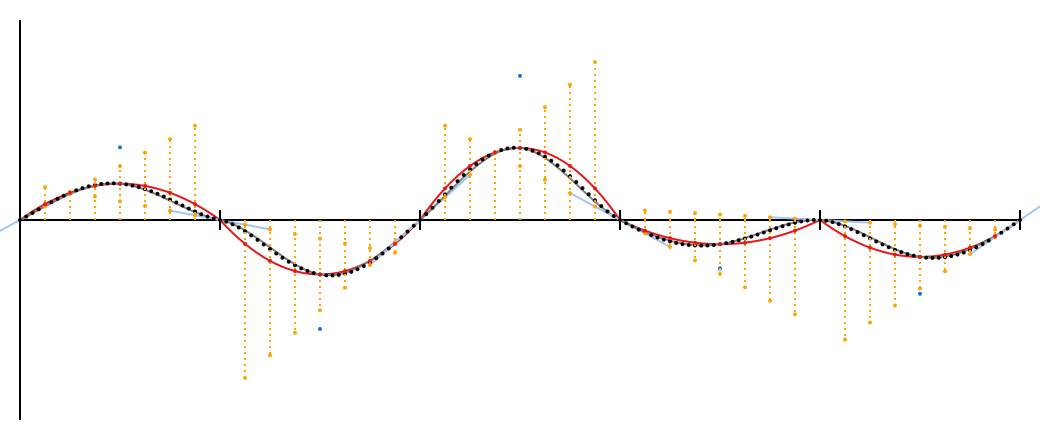
Новые точки близки к красным квадратичным кривым, но в районе засечек они ближе прилегают к исходным голубым направляющим. Средние точки точно совпадают, потому что smoothstep не изменяет $½$ .

(Теперь уравнение кривой для каждого сегмента выглядит как $y=2(a - b)x^4 - (3a - 5b)x^3 - 3bx^2 + ax$ , хрен выговоришь. Не постесняйтесь взять производную и убедиться, что в концах сегмента она в точности равна $a$ и $b$ .)

Если вы хотите получить лучшее интуитивное понимание происходящего, вот тот же график, только интерактивный! Кликайте и перетаскивайте, чтобы поиграться с наклонами.

Октавы

Вы могли заметить, что эти гладкие возвышенности и впадины не так уж похожи на «облачный» шум, который я рекламировал в начале статьи.

Внезапно, «облачность» не является частью шума Перлина. Это хитрая штука, которую можно сделать на его основе.

Создайте другую кривую Перлина (или переиспользуйте ту же самую), но удвойте разрешение — теперь случайные наклонные прямые будут в точках $x = 0, ½, 1, …$ . Поделите на два выходные значения и прибавьте к исходной кривой. Получится что-то вроде этого:

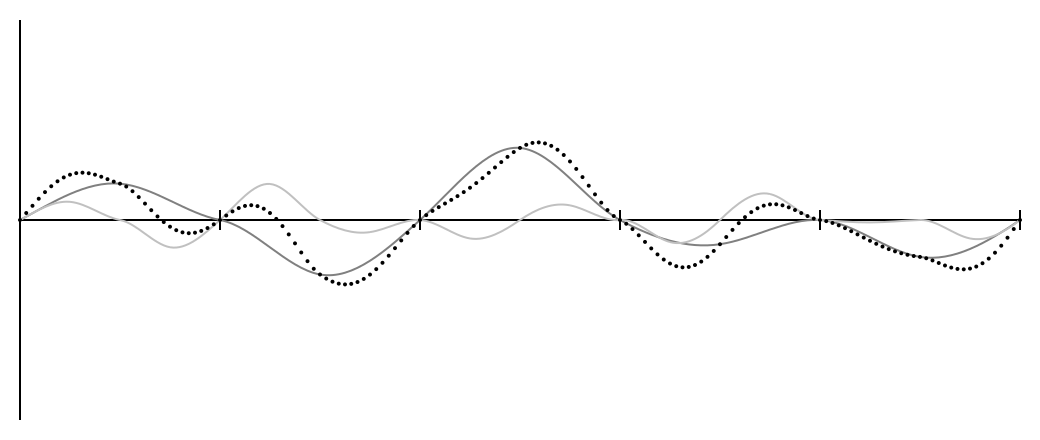
Весь график был уменьшен до половинного размера и повторён дважды.

Вы можете повторить это сколько угодно раз, делая каждый новый график вдвое меньше предыдущего. Каждый отдельный график называется октавой (как в музыке, где каждая октава имеет частоту в два раза больше предыдущей), и результаты получаются приятными и шероховатыми после 4–5 октав.

Расширяемся до 2D

Идея та же самая, но вместо числовой оси с наклонными линиями мы имеем на входе сетку.
Также для расширения понятия «наклона» в двух изменениях, в каждом узле сетки появляется вектор:

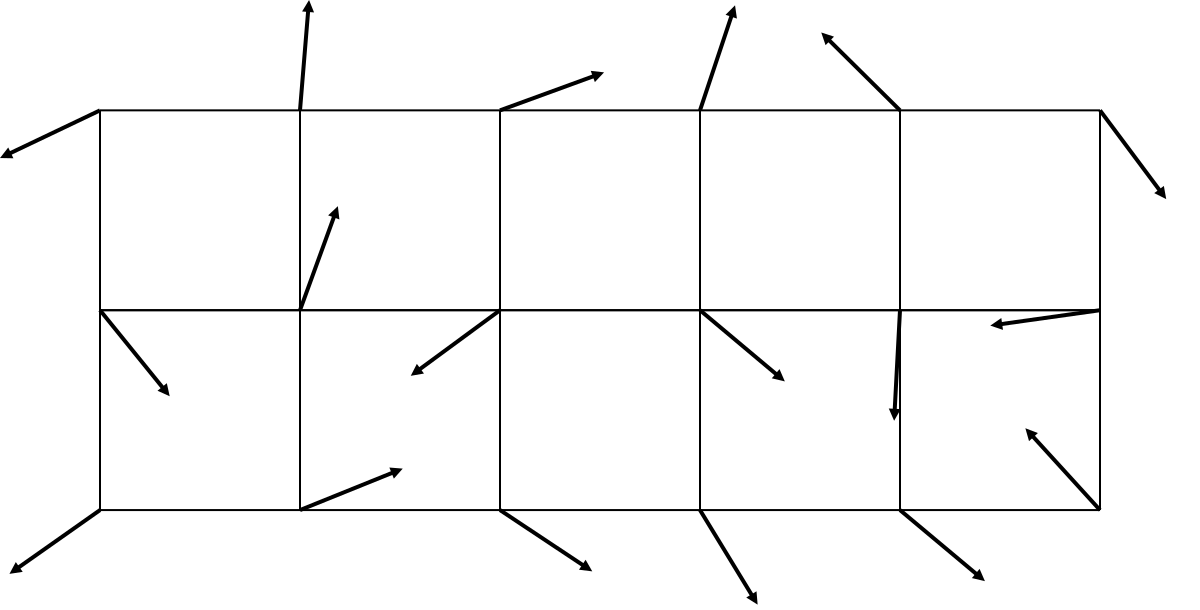
Я укоротил стрелочки, чтобы они влезли на картинку и не перекрывали друг друга, но имеется в виду, что изображены единичные векторы — то есть, каждый вектор на самом деле имеет длину 1, и нам важна только информация о направлении, не о длине. Про генерацию векторов я расскажу позже.

Выглядит похоже, но здесь есть важное различие. Раньше вход был горизонтальным — позиция на оси абсцисс — и выход был вертикальным. Сейчас вход двумерный — где мы?

Грубый алгоритм того, что мы делали раньше:

Найти расстояние до ближайшей точки слева и умножить его на наклон в этой точке.
Сделать то же самое для точки справа.
Интерполировать эти значения.

Здесь требуется пара больших изменений для того, чтобы алгоритм заработал в двух измерениях. Каждая точка теперь имеет четыре соседних узла сетки, и всё ещё требуется какое-то подобие произведения наклона на расстояние.

Решение состоит в использовании скалярных произведений. Если у вас есть два вектора $(a, b)$ и $(c, d)$ , их скалярное произведение равняется сумме попарных произведений соответствующих компонент: $ac + bd$ . В диаграмме выше, каждая точка сетки имеет два исходящих вектора: случайный и указывающий на текущую точку. Произведение наклона на расстояние может быть заменено скалярным произведением этих двух векторов.

Но почему? Хороший вопрос.

Геометрическое объяснение скалярного произведения говорит, что это произведение длин векторов на косинус угла между ними. Это ничего толком не проясняет для меня, и невозможно нарисовать здесь наглядный график, но давайте немного над этим поразмыслим.

Все наши случайные вектора являются единичными, их длина равна 1. Это не даёт никакого вклада в произведение. Поэтому остаётся (скалярное) расстояние от текущей точки до точки сетки, помноженное на косинус угла между векторами.

Косинус говорит вам, насколько мал этот угол — или, в нашем случае, насколько близки два вектора. Если они указывают в одном направлении, косинус равен единице. По мере их удаления, косинус уменьшается: для прямого угла он обращается в ноль (и скалярное произведение равно нулю), и если они указывают в противоположные стороны, косинус будет равен –1.

Чтобы визуализировать, что это значит, я нарисовал единственное скалярное произведение между точкой и ближайшим к ней узлом сетки. Это эквивалент оранжевых точек с одномерного графика.

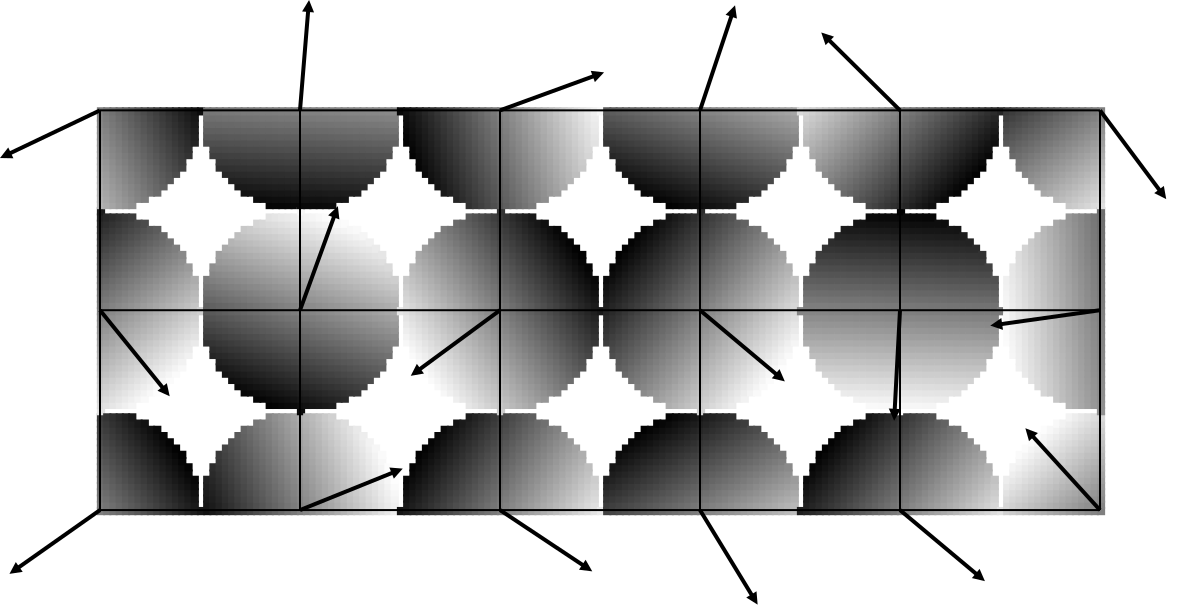
Это уже выглядит интересно. Помните, это что-то вроде трёхмерного графика, на который мы смотрим сверху. Координаты $x$ и $y$ — это вход, точки, которые мы выбрали, и координата $z$ — это выход. Обычно её рисуют в оттенках серого, как я сделал здесь, но вы можете также её отобразить как глубину. Белые точки выходят из экрана в вашу сторону, серые уходят вглубь экрана.

В этом смысле, каждый узел сетки имеет наклонную плоскость, прикреплённую к нему, в отличие от наклонных линий в одномерном случае. Вектор указывает в сторону белого конца, того конца, который торчит из экрана в вашу сторону. Для точек, близких к узлу сетки, скалярное произведение близко к нулю, как и на одномерном графике; для точек подальше от нуля значения ближе к экстремумам.

Возможно, для вас не будет сюрпризом, если я скажу, что случайные вектора в этом случае называют градиентами.

Теперь, когда в каждой точке есть четыре скалярных произведения, нам нужно их как-то скомбинировать. Линейная интерполяция работает только для двух значений, поэтому мы будем делать её попарно. Один раунд интерполяции оставит нас с двумя значениями, второй даст одно значение, которое и будет нашим выходом.

Я пытался сделать диаграмму, изображающую промежуточное состояние, чтобы показать, как комбинировать несколько градиентов, но не смог придумать что-то осмысленное.

Взамен примите эту интерактивную сетку с шумом Перлина, где также можно потаскать стрелочки и увидеть, как это влияет на итоговый узор.

Три и более измерений

С этого момента совсем не сложно расширить идею на произвольное количество измерений.
Выберите больше единичных векторов в нужном количестве измерений, вычислите больше скалярных произведений, интерполируйте.

Не забудьте про одну вещь: каждый раунд интерполяции должен «схлопывать» одну из осей.

Рассмотрим плоскость, где нужно вычислить скалярные произведения для четырёх точек: верхняя левая, верхняя правая, нижняя левая, нижняя правая. Два измерения, два раунда интерполяции.

Вы можете интерполировать между собой две верхних точки и две нижних точки; это «схлопнет» горизонтальную ось и оставит только два значения, верхнее и нижнее. Или можно сделать наоборот, «схлопнуть» левые и правые точки, избавившись от вертикальной оси и оставив левую и правую точки. Оба способа хороши.

Но что точно вы не можете сделать — интерполяцию крест накрест. Вам нужно знать, с каким коэффициентом интерполировать, то есть, насколько далеко вы от каждой точки. Горизонтальная интерполяция хороша, поскольку мы знаем расстояние по горизонтали до узлов сетки. Вертикальная интерполяция хороша, поскольку мы знаем расстояние по вертикали. Интерполяция по диагонали? Что это значит? Какое значение принимает $t$ ? Даже если нам это удастся, как мы проведём второй раунд интерполяции?

В трёх и более измерениях немного труднее отслеживать такие вещи, так что будьте настороже.

Вариации

Идея шума Перлина довольно проста, и для получения различных эффектов можно изменить почти любую её часть.

Выбор градиентов

Я знаю три способа выбора градиентов.

Самый очевидный способ — выбрать $n$ случайных чисел из диапазона $[-1; 1]$ (для $n$ измерений), использовать теорему Пифагора для нахождения длины вектора, нормировать вектор на длину. Вуаля, у вас есть единичный вектор. Так делается и в оригинальном коде Кена Перлина.

Оно работает, но даёт больше диагональных векторов, чем направленных вдоль осей, по той же причине что и бросок двух костей чаще всего будет давать сумму в 7 очков. Вам нужен случайный угол, а не координата.

Для двух измерений это легко: возьмите случайный угол! Выберите случайное число из диапазона $[0; 2\pi]$ . Назовите его $\theta$ . Ваш вектор $(cos \theta, sin \theta)$ . Готово.

Для трёх измерений… эм.

Ладно, я поискал на MathWorld и нашёл решение, которое, как мне кажется, работает в любом измерении. Принцип прежний: взять n случайных чисел и нормировать вектор, полученный из них. Отличие в том, что числа берутся из нормального распределения — то есть, используется распределение Гаусса. В Python для этого есть функция random.gauss (); в C, ну я думаю, можно имитировать эту функцию, вычислив сумму кучи чисел из равномерного распределения. Всё равно идея заключается в бросании кости много раз.

Это плохо работает для одного измерения, где нормировка всегда даст 1 или –1, и результат будет выглядеть ужасно. В этом случае просто нужно взять одно случайное число.

Третий метод, предложенный Кеном Перлином в работе «Improving Noise», предлагает вообще не выбирать случайные градиенты! Вместо этого используйте фиксированный набор векторов и выбирайте случайный из них.

Зачем так делать? Одна из причин — решить проблему «слипания», которая, я полагаю, частично была обусловлена смещением ориентации градиентов в сторону диагональных. Но другой причиной была…

Оптимизация

Я забыл упомянуть ключевую особенность оригинальной реализации Кена Перлина. Она не создавала набор случайных градиентов для каждого узла сетки; она создавала набор случайных градиентов фиксированного размера, затем использовала схему выбора из этого набора градиента для каждого отдельно взятого узла сетки. Это экономило память и работало очень быстро, но всё ещё позволяло точкам иметь произвольно низкие или высокие значения.

Предложение по «улучшению» покончило со случайными градиентами насовсем, предлагая вместо них (для трёхмерного случая) набор из 16 градиентов, у которых одна координата равна нулю, а две других принимают значения $\pm1$ . Эти вектора больше не единичны, зато скалярные произведения гораздо легче считать. Элемент случайности обеспечивается схемой выбора градиента в каждом конкретном узле сетки. Для генерации больших кусков шума оказалось, что это работает неплохо.

Никакая из этих оптимизаций не является необходимой для получения шума Перлина, но возможно они вам пригодятся, если вы собираетесь генерировать много шума в реальном времени.

Smootherstep

Выбор функции smoothstep довольно произволен; можно использовать любую функцию, которая сплющивается в нуле и единице.

«Improving Noise» предлагает альтернативу под названием smootherstep, которая выглядит так: $6x^5 - 15x^4 + 10x^3$ . Можно создать похожие полиномы более высокого порядка, хотя они, конечно же, увеличат время работы алгоритма.

Нет причин не использовать, скажем, интерполяцию синусоидой: $½sin(\pi(x - ½)) + ½$ . Несмотря на свою непрактичность и значительно более низкую скорость по сравнению с полиномами, это вполне валидный вариант интерполяции.

По мне так всё довольно похоже. У smootherstep более резкие экстремумы, что выглядит чуть интереснее.

Октавы

В использовании октав нет ничего необычного; это всего лишь простой фрактал. При добавлении всё более детализированного шума меньшей амплитуды возможно получить что-то интересное.

В этой презентации Кена Перлина есть несколько примеров, таких как взятие модуля каждой октавы перед сложением для добавления эффекта турбулентности, или взятие синуса для эффекта завихрённого мрамора.

Бросьте сюда математики и посмотрите, что произойдёт. Математика для того и нужна!

Замощение

Замостите пространство сеткой градиентов, и получите замощение шумом. Легче некуда.

Симплекс-шум

В высших измерениях, даже поиск шума для одной точки требует много математики. Даже в трёх измерениях есть восемь окружающих точек: восемь скалярных произведений, семь линейных интерполяций, три раунда smoothstep.

Симплекс-шум является вариацией, которая использует треугольники вместо квадратов. В трёх измерениях это тетраэдр, которому нужно всего 4 точки вместо 8. В четырёх изменениях нужно 5 точек вместо 16.

Мне никогда ещё не потребовалось столько шума, чтобы иметь вескую причину писать реализацию этого алгоритма, но для генерации четырёх- или пятимерного шума может быть полезно.

Некоторые свойства

Значение шума Перлина в каждом узле сетки при любом числе измерений равно нулю.

Шум Перлина непрерывен — нигде нет резких перепадов. Даже при использовании огромного количества октав, неважно, насколько рваным выглядит результат, при достаточном увеличении можно увидеть, что кривая всё равно гладкая.

Вопреки распространённому мнению — которое даже поддерживал Кен Перлин! — область значений шума Перлина не равна $[-1; 1]$ . Она равна $\pm½\sqrt{n}$ , где $n$ — число измерений. Для одномерного случая этот диапазон равен $[-½; ½]$ (я уверен, что вы это легко докажете, если немного подумаете), а знакомый двумерный шум зажат в диапазоне $\pm½\sqrt{2} \approx \pm0.707$ (что легко доказывается аналогичным способом). Если вы используете шум Перлина и хотите, чтобы он занял определённый диапазон, не забудьте это учесть.

Октавы, конечно, изменят выходной диапазон. Одна октава увеличит его на 50%; две — на 75%; три — на 87.5% и так далее.

Выход шума Перлина не распределен равномерно, даже для больших выборок. Вот гистограмма однооктавного двумерного шума Перлина, сгенерированного в GIMP:

Я без понятия, что это за распределение; точно не нормальное. В частности, заметьте, что верхние и нижние ⅛ значений фактически не существуют. Если вы играетесь с интерактивным двумерным демо, вы могли выяснить, почему так происходит: получить яркий белый можно только если все четыре градиента в квадрате будут указывать точно в центр, а чёрный — если все будут указывать наружу. Оба этих события маловероятны.

Если вы хотите больше веса на краях, попробуйте скормить шум функции, которая смещает выход к крайним точкам… например, smoothstep. Не забудьте только сначала нормализовать к диапазону $[0, 1]$ .

Удивительно, добавление октав не сильно меняет распределение, если масштабировать всё к тому же диапазону.

Есть множество применений шума Перлина. Я видел деревянную текстуру, полученную при помощи использования модульной арифметики. Я использовал её для создания пути через roguelike-лес. Вы можете легко получить облака, обрезав шум по произвольному уровню. Дым в Under Construction — это шум Перлина, в котором положительные значения соответствуют дыму, а отрицательные выброшены.

Благодаря непрерывности, можно использовать одно измерение в качестве оси времени и получить шум, который будет плавно меняться во времени. Вот анимация шума, где каждый кадр — это плоский срез трехмерного (замощённого) блока шума:

Дайте мне уже код

Хорошо, вот, пожалуйста, конечно. Вот реализация на Python. Не знаю, смогу ли я обосновать выделение в отдельный модуль, да и как-то лень.

Некоторые прикольные штуки:

Неограниченный диапазон
Неограниченные измерения
Встроенная поддержка октав
Встроенная поддержка замощения
Куча комментариев, некоторые могут даже быть истинными
Возможно, слишком медленно

Вот код, который создаёт вышеупомянутую анимацию:

from perlin import PerlinNoiseFactory
import PIL.Image

size = 200
res = 40
frames = 20
frameres = 5
space_range = size//res
frame_range = frames//frameres

pnf = PerlinNoiseFactory(3, octaves=4, tile=(space_range, space_range, frame_range))

for t in range(frames):
    img = PIL.Image.new('L', (size, size))
    for x in range(size):
        for y in range(size):
            n = pnf(x/res, y/res, t/frameres)
            img.putpixel((x, y), int((n + 1) / 2 * 255 + 0.5))

    img.save("noiseframe{:03d}.png".format(t))
    print(t)

Выполняется за 1:40 на PyPy 3.